ознайомившись із ними, не можна як слід зрозуміти все значення математики для природознавства, і техніки і навіть повністю оцінити всю красу і принадність самої математичної науки.
А.М. Колмогоров
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Операції диференціювання. Первісна функція презентация
Содержание
- 1. Операції диференціювання. Первісна функція
- 2. Операції в математиці Кожна дія (операція) в
- 3. Основна операція диференціального числення є знаходження похідної
- 4. Первісна Означення. Первісною для даної функції y=f(x)
- 5. Таблиця первісних
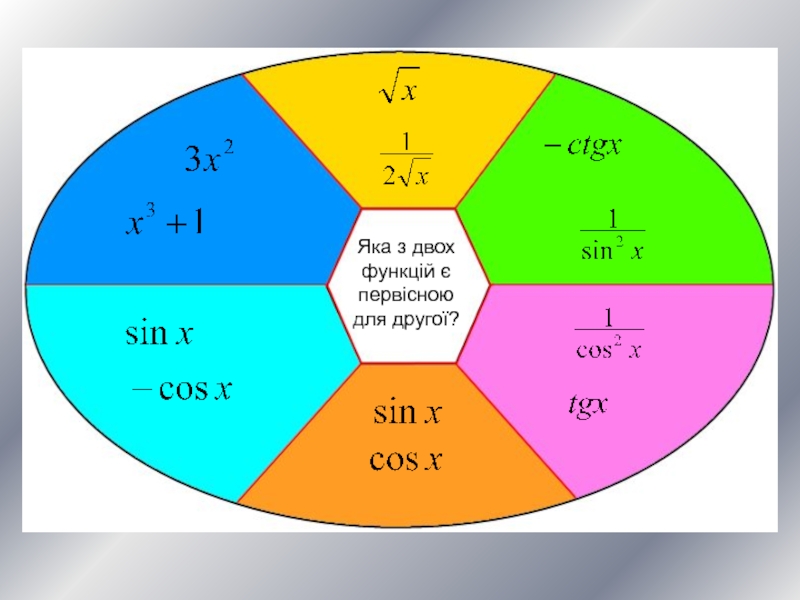
- 6. Яка з двох функцій є первісною для другої?
- 7. Вказати первісну F для кожної даної функції f
- 8. ОСНОВНА ВЛАСТИВІСТЬ ПЕРВІСНОЇ: Якщо на проміжку
- 9. Яка з функцій є первісною
- 10. x y F(x)=x2+2 F(x)=x2 F(x)=x2-4 F(x)=x2-7 F(x)=x2-2
- 11. Завдання. Побудувати графік первісної для функції f(x)=2x,
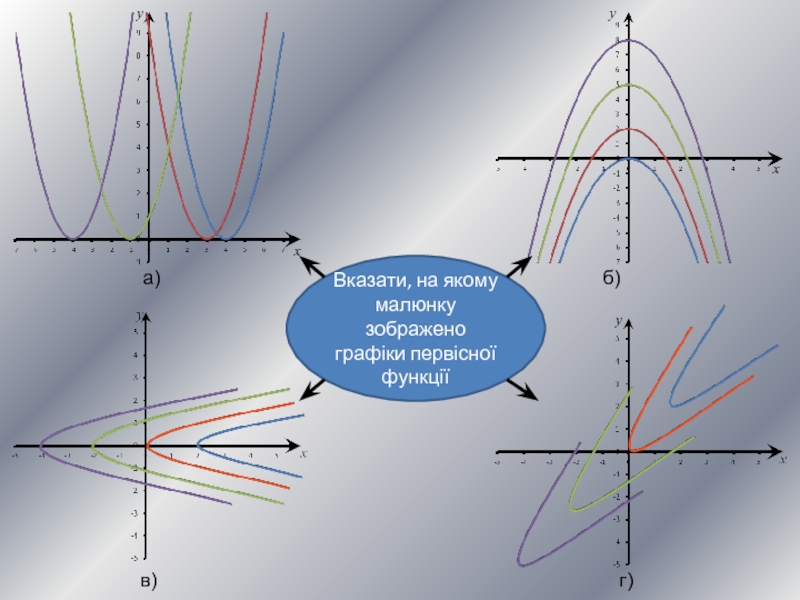
- 12. x y x y Вказати, на якому
- 13. Завдання. На малюнку зображено первісну функції
- 14. Правила знаходження первісної Приклад: І правило знаходження
Слайд 2Операції в математиці
Кожна дія (операція) в математиці має обернену:
додавання-віднімання;
множення-ділення;
піднесення до степеня
– добування кореня;
логарифмування – потенціювання;
множення одночлена на многочлен - розкладання многочлена на множники способом винесення спільного множника за дужки.
Деякі з обернених операцій виявилися неоднозначними:
є числа 5 і -5, бо
логарифмування – потенціювання;
множення одночлена на многочлен - розкладання многочлена на множники способом винесення спільного множника за дужки.
Деякі з обернених операцій виявилися неоднозначними:
є числа 5 і -5, бо
Слайд 3Основна операція диференціального числення є знаходження похідної
даної функції
Обернена операція до диференціювання є: за відомою похідною деякої функції знайти (відновити) саму функцію , яку називають первісною F для відомої функції . Операція знаходження первісної F для даної функції
називається інтегруванням.
Отже, інтегрування є оберненою операцією до операції диференціювання.
Обернена операція до диференціювання є: за відомою похідною деякої функції знайти (відновити) саму функцію , яку називають первісною F для відомої функції . Операція знаходження первісної F для даної функції
називається інтегруванням.
Отже, інтегрування є оберненою операцією до операції диференціювання.
Слайд 4Первісна
Означення. Первісною для даної функції y=f(x) на заданому проміжку [a; b]
називається така функція F(x), похідна якої для всіх x з інтервалу [a; b] дорівнює f(x), тобто Fʹ(x)=f(x) для всіх x є [a; b].
Наприклад, функція F(x)=x2 є первісною для функції f(x)=2x на проміжку (-∞;∞), оскільки на цій множині виконується рівність (x2)ʹ=2x.
Для функції f(x)=2x первісними будуть функції F(x)=x2+1;F(x)=x2-10; і т.д., тобто загальний вигляд первісних для функції f(x)=2x матимуть вигляд F(x)=x2+С, де С – довільна стала.
Отже, операція інтегрування неоднозначна.
Наприклад, функція F(x)=x2 є первісною для функції f(x)=2x на проміжку (-∞;∞), оскільки на цій множині виконується рівність (x2)ʹ=2x.
Для функції f(x)=2x первісними будуть функції F(x)=x2+1;F(x)=x2-10; і т.д., тобто загальний вигляд первісних для функції f(x)=2x матимуть вигляд F(x)=x2+С, де С – довільна стала.
Отже, операція інтегрування неоднозначна.
Слайд 8ОСНОВНА ВЛАСТИВІСТЬ
ПЕРВІСНОЇ:
Якщо на проміжку
функція F(x) є первісною для f(x), то на цьому проміжку первісною для f(x) буде також функція F(x)+C
Первісні однієї і тієї ж функції можуть відрізнятись лише на сталий доданок
Слайд 10x
y
F(x)=x2+2
F(x)=x2
F(x)=x2-4
F(x)=x2-7
F(x)=x2-2
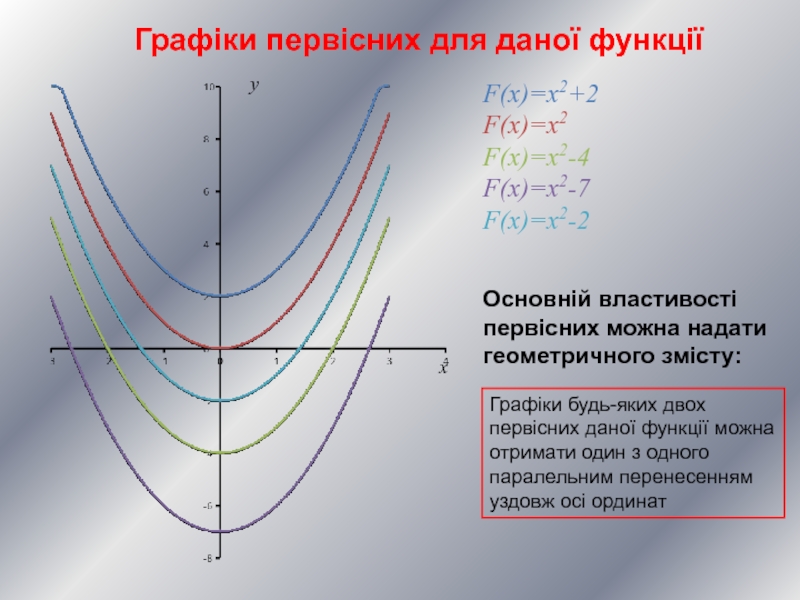
Графіки первісних для даної функції
Основній властивості первісних можна надати геометричного змісту:
Графіки
будь-яких двох первісних даної функції можна отримати один з одного паралельним перенесенням уздовж осі ординат
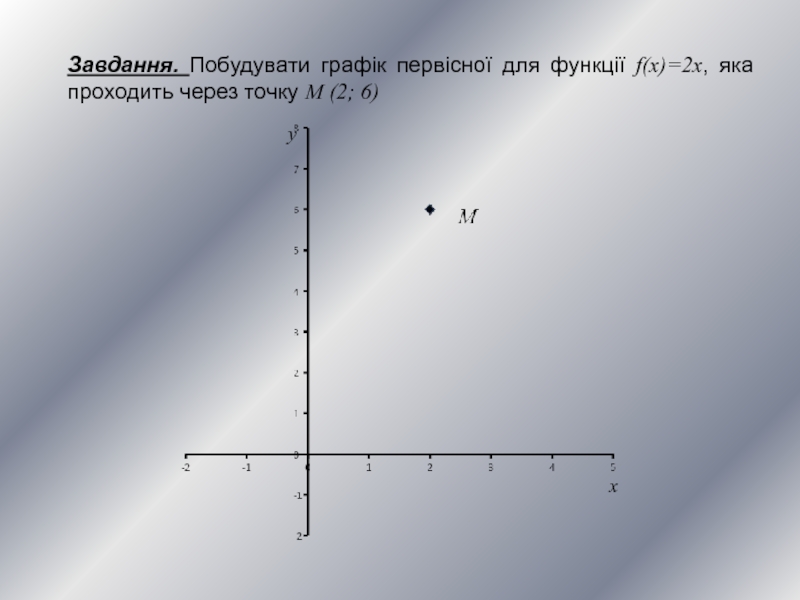
Слайд 11Завдання. Побудувати графік первісної для функції f(x)=2x, яка проходить через точку
M (2; 6)
x
y
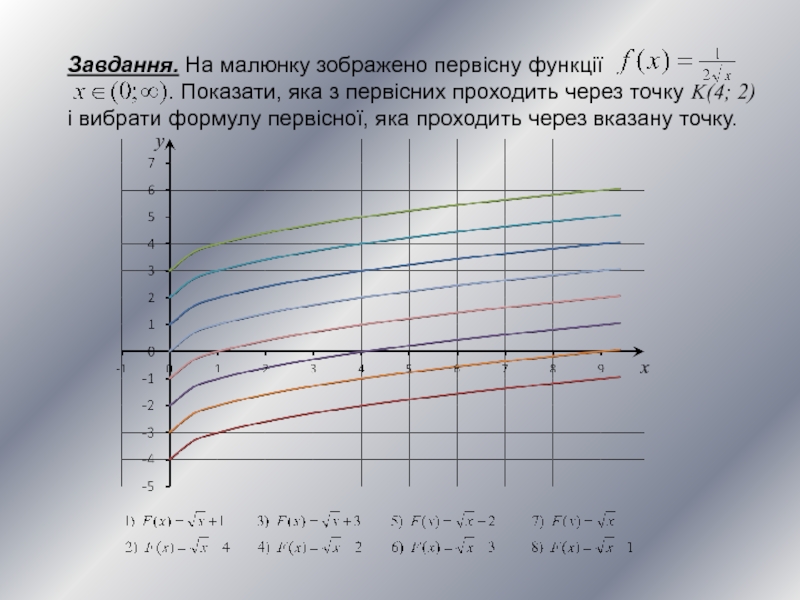
Слайд 13Завдання. На малюнку зображено первісну функції
. Показати, яка з первісних проходить через точку K(4; 2) і вибрати формулу первісної, яка проходить через вказану точку.
x
y
Слайд 14Правила знаходження первісної
Приклад:
І правило знаходження первісної
ІІ правило знаходження первісної
ІІІ правило знаходження
первісної
Приклад:
Приклад:



![ПервіснаОзначення. Первісною для даної функції y=f(x) на заданому проміжку [a; b] називається така функція F(x),](/img/tmb/4/318640/02e025799d57fe6defbedf1dad7355e1-800x.jpg)