- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямоугольный треугольник. Признаки равенства прямоугольных треугольников презентация
Содержание
- 1. Прямоугольный треугольник. Признаки равенства прямоугольных треугольников
- 2. Тема урока: Прямоугольный треугольник. Признаки равенства прямоугольных
- 3. Повторение. Тест. Домашние задачи у
- 4. Тест 3 1 2 4
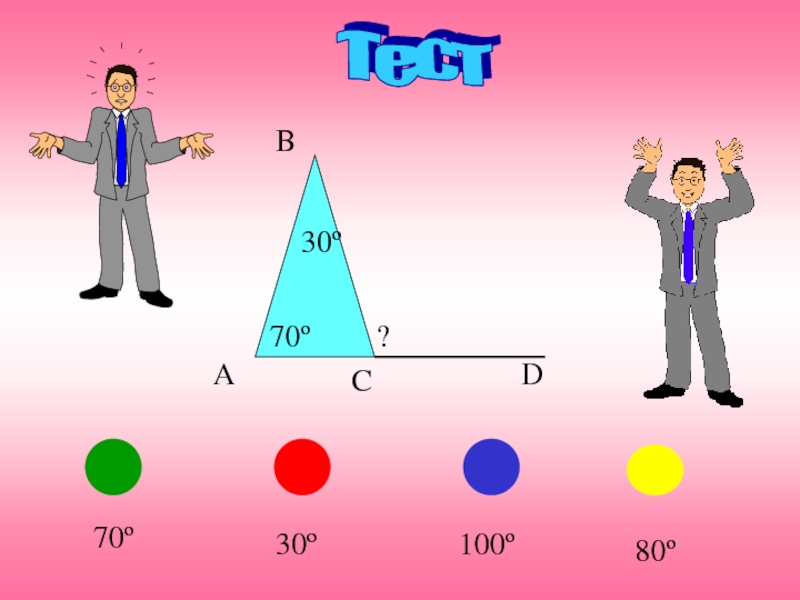
- 5. Тест 100º 70º 30º 80º
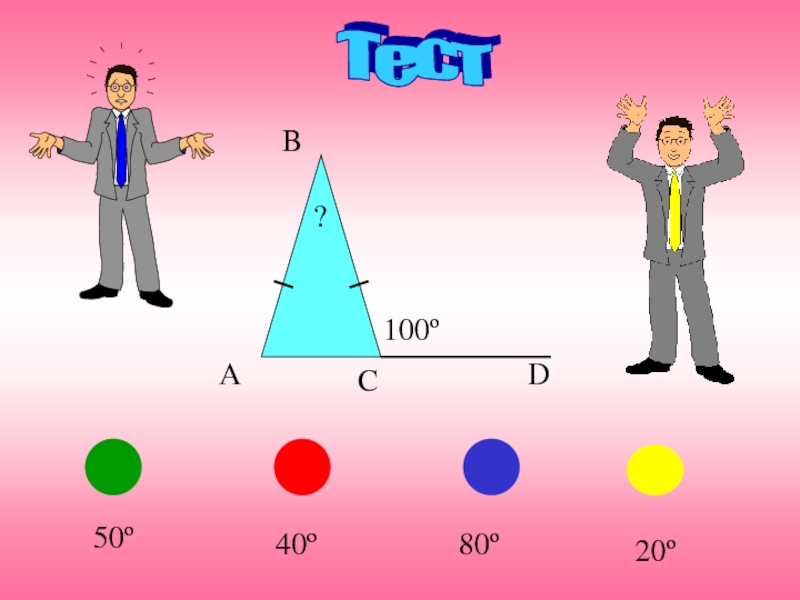
- 6. Тест A B C D
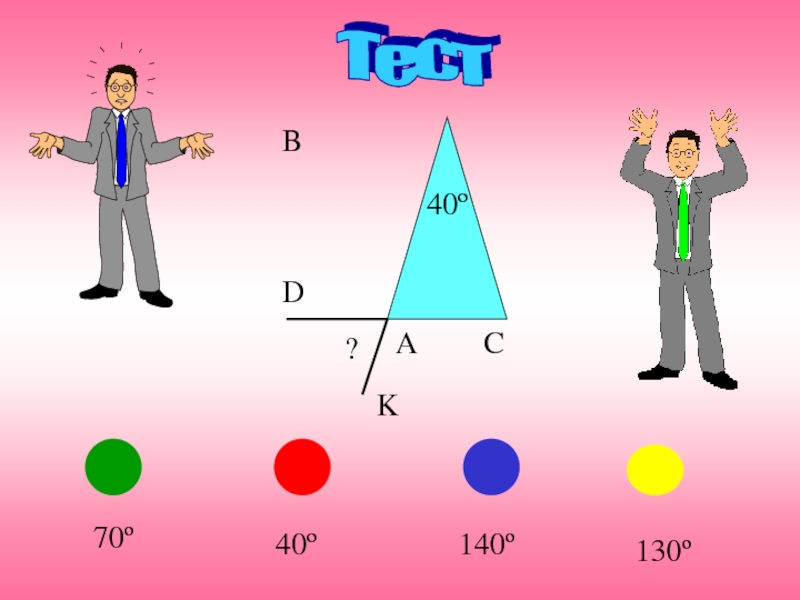
- 7. Тест B 140º 70º 40º 130º K
- 8. Прямоугольный треугольник Прямоугольный треугольник
- 9. Треугольник называется прямоугольным, если у него есть
- 10. Сторона прямоугольного треугольника, противолежащая прямому углу называется гипотенузой. Две другие стороны называются катетами.
- 11. Найдите острые углы прямоугольных треугольников.
- 12. Признаки равенства прямоугольных треугольников Признаки равенства прямоугольных треугольников
- 13. Если два катета одного прямоугольного треугольника соответственно
- 14. Если гипотенуза и острый угол одного прямоугольного
- 15. Если катет и прилежащий к нему острый
- 16. Если катет и противолежащий острый угол одного
- 17. Если гипотенуза и катет одного прямоугольного треугольника
- 18. Домашнее задание Вопросы №14,15,16. Формулировки признаков. Задачи №40, 41(2).
- 19. Урок №2 по теме "Прямоугольный треугольник".
- 20. по двум катетам по гипотенузе и острому
- 21. Тест Выбери правильное завершение определения. Катетом
- 22. Тест Выбери правильное завершение определения. Гипотенузой
- 23. Тест Выбери правильное завершение определения. Сумма острых углов прямоугольного треугольника равна …
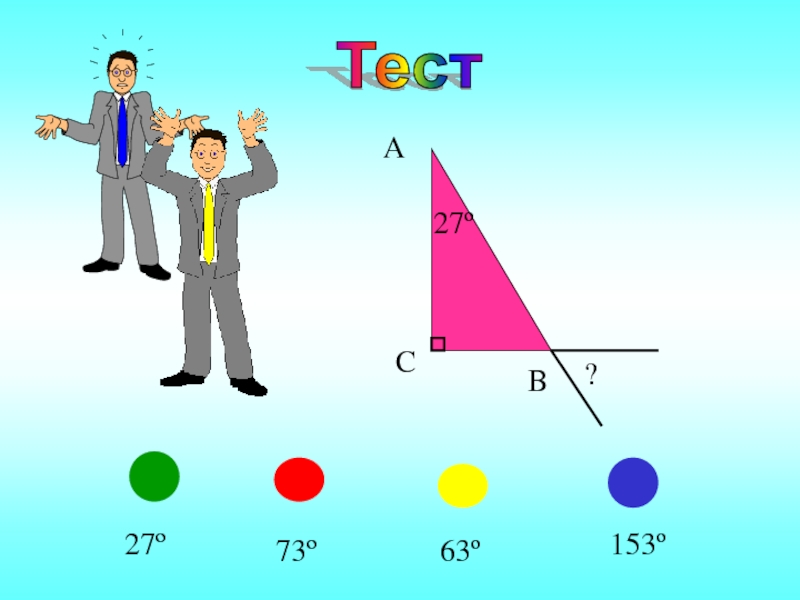
- 24. Тест 153º
- 25. Чему равны углы при основании в
- 26. Задача №1. Доказательство.
- 27. Из точки D, лежащей на биссектрисе ∠
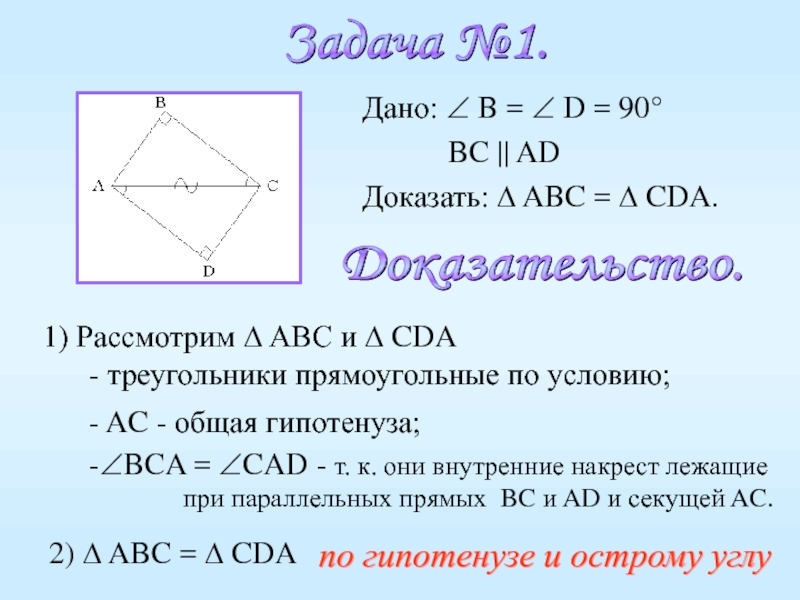
- 28. Дано: ∠C = ∠D = 90°
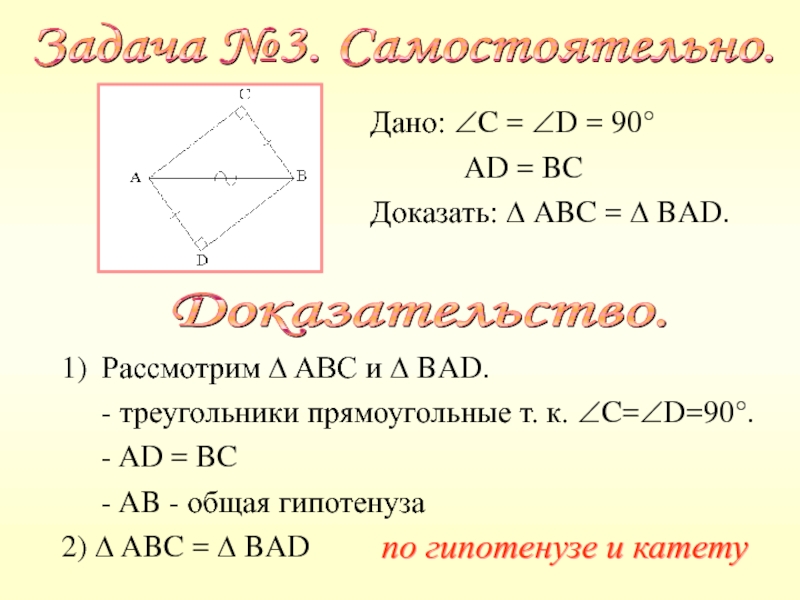
- 29. Задача №4. Решение. 1) Рассмотрим
- 30. Домашнее задание. Дано: DA ⊥ AB
- 31. Cвойство катета, лежащего против угла в 30 градусов. Тема урока
- 32. BC
- 33. Дано: Δ ABC
- 34. Дано: Δ ABC - равнобедренный
- 35. Решение. Δ ABC – равнобедренный
- 36. по двум катетам по гипотенузе и острому
- 37. Докажите, что у равных треугольников высоты, проведенные
- 38. Повторение. №2. Докажите, что сумма
- 39. Домашнее задание. Устно: формулировки признаков и формулировка
- 40. BC
Слайд 2Тема урока:
Прямоугольный треугольник.
Признаки равенства прямоугольных треугольников.
Тема урока:
Прямоугольный треугольник.
Признаки равенства прямоугольных треугольников.
Слайд 3Повторение. Тест.
Домашние задачи у доски.
Признаки равенства прямоугольных треугольников.
Решение задач.
План
Слайд 9Треугольник называется прямоугольным, если у него есть прямой угол.
ABC – прямоугольный
∠ C = 90°
∠ A + ∠ B = 90°
Сумма острых углов прямоугольного треугольника равна 90°.
Определение.
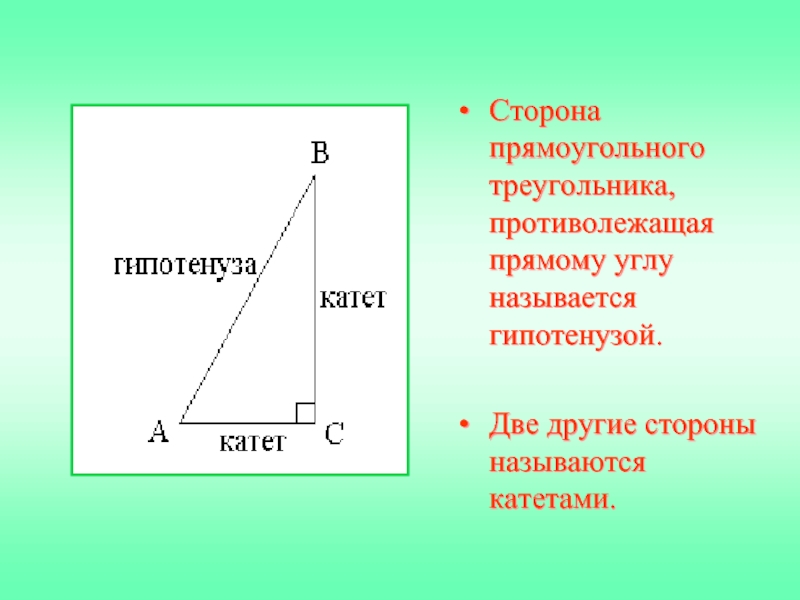
Слайд 10Сторона прямоугольного треугольника, противолежащая прямому углу называется гипотенузой.
Две другие стороны называются
Слайд 11
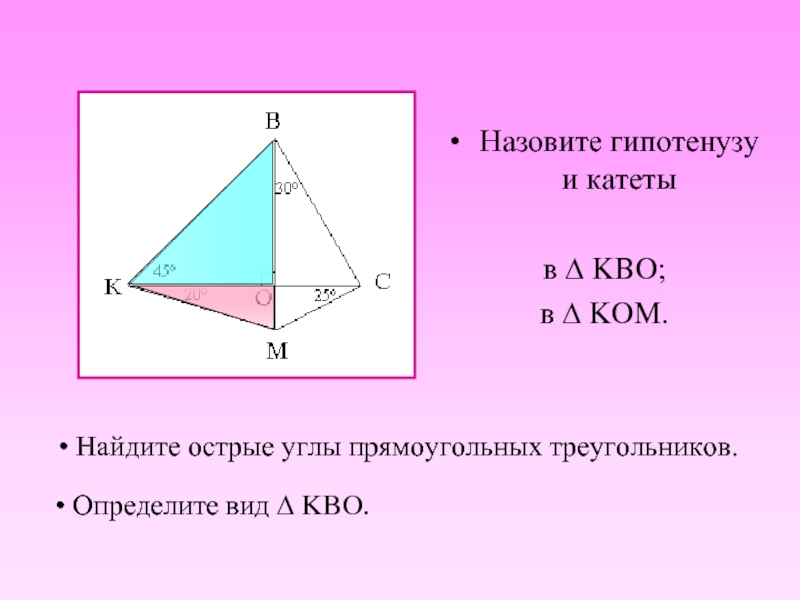
Найдите острые углы прямоугольных треугольников.
Назовите гипотенузу и катеты
в Δ KBO;
в
Определите вид Δ KBO.
Слайд 12Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Слайд 13Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого
по двум катетам
по двум сторонам и углу между ними
Слайд 14Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе
по гипотенузе и
острому углу
по стороне и двум
прилежащим к ней углам
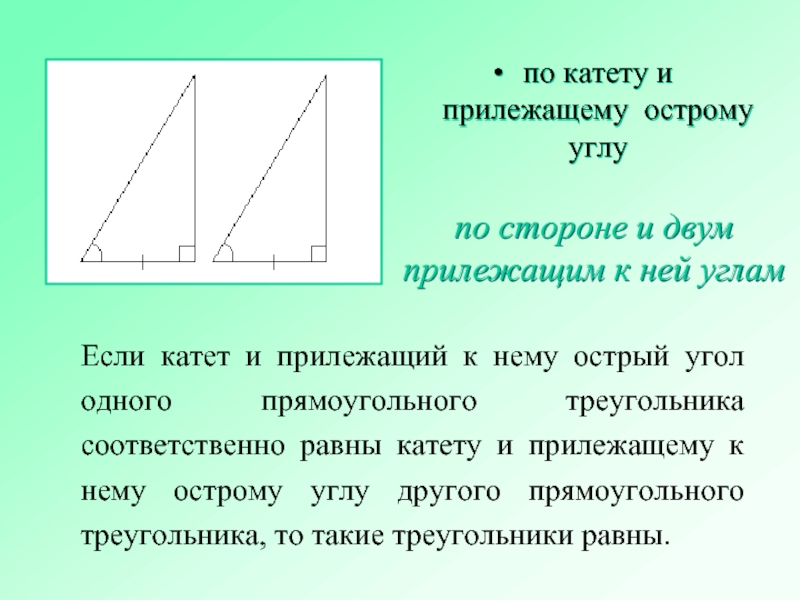
Слайд 15Если катет и прилежащий к нему острый угол одного прямоугольного треугольника
по катету и прилежащему острому углу
по стороне и двум прилежащим к ней углам
Слайд 16Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны
по катету и противолежащему острому углу
по стороне и двум прилежащим углам
Слайд 17Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и
по гипотенузе и катету
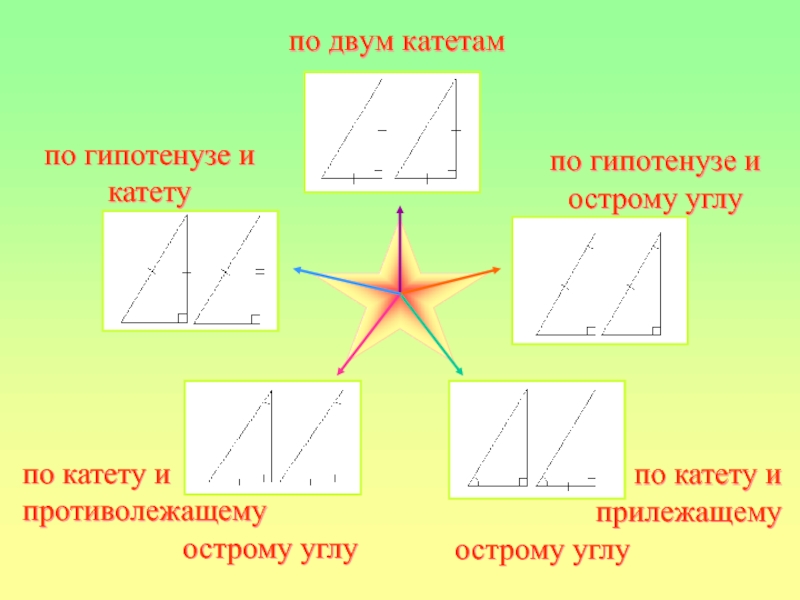
Слайд 20по двум катетам
по гипотенузе и острому углу
по катету и
прилежащему
острому
по катету и
противолежащему
острому углу
по гипотенузе и катету
Слайд 21Тест
Выбери правильное завершение определения.
Катетом называется…
Любая сторона треугольника;
Сторона, лежащая против прямого
Перпендикуляр из вершины угла на противолежащую сторону;
Сторона, примыкающая к вершине прямого угла.
Слайд 22Тест
Выбери правильное завершение определения.
Гипотенузой называется…
Любая сторона треугольника;
Сторона, лежащая против прямого
Перпендикуляр из вершины угла на противолежащую сторону;
Сторона, примыкающая к вершине прямого угла.
Слайд 23Тест
Выбери правильное завершение определения.
Сумма острых углов прямоугольного треугольника равна …
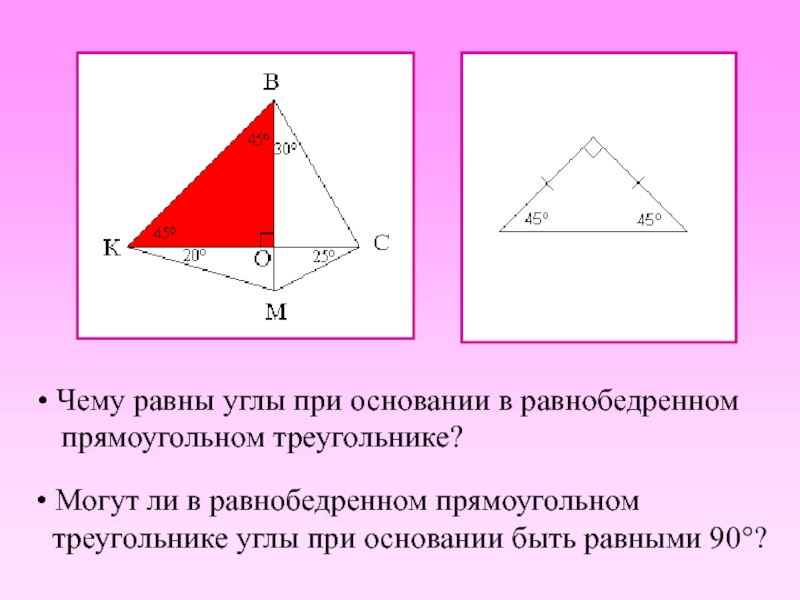
Слайд 25 Чему равны углы при основании в равнобедренном
прямоугольном треугольнике?
треугольнике углы при основании быть равными 90°?
Слайд 26
Задача №1.
Доказательство.
1) Рассмотрим Δ ABC и Δ CDA
- треугольники прямоугольные по условию;
Слайд 27Из точки D, лежащей на биссектрисе ∠ A, опущены перпендикуляры DB
Задача №2.
Доказательство.
1) Рассмотрим Δ ADB и Δ ADC.
- треугольники прямоугольные т. к. DB⊥AB, DC⊥AC.
2) Δ ADB = Δ ADC по гипотенузе и острому углу.
- AD - общая гипотенуза.
Слайд 29Задача №4.
Решение.
1) Рассмотрим ΔABO и ΔDCO.
2) ΔABO = ΔDCO
3) Из равенства треугольников следует AB = CD = 3 см.
• AO = OD т. к. O - середина AD.
• треугольники прямоугольные т. к. AB⊥BC и CD⊥BC.
Слайд 30Домашнее задание.
Дано: DA ⊥ AB
BD = AF
Доказать: Δ ABD = Δ BAF
Устно: формулировки признаков.
№1.
№2. Докажите, что два равнобедренных прямоугольных треугольника равны, если равны их гипотенузы.
№3 Докажите равенство прямоугольных треугольников по катету и высоте, опущенной на гипотенузу.
Письменно:
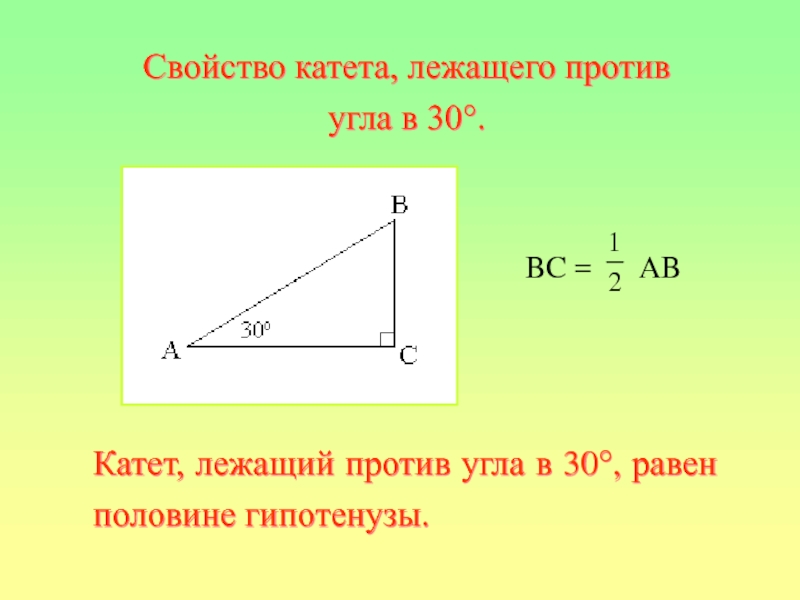
Слайд 32 BC = AB
Катет,
Свойство катета, лежащего против угла в 30°.
Слайд 33Дано: Δ ABC
∠ C
Доказать: АС = АВ.
Докажите, что в прямоугольном треугольнике с углом 30° катет, противолежащий этому углу, равен половине гипотенузы.
Доказательство.
Задача №43
Слайд 34Дано: Δ ABC - равнобедренный
с основанием
∠ B =120°;
BD - медиана; BD = 3 см.
Найти: ∠ A, ∠ C, AB и BC.
Задача №1.
Решение.
В равнобедренном треугольнике угол, противолежащий основанию, равен 120°, а медиана, проведенная к основанию, равна 3 см. Найдите углы при основании и боковые стороны треугольника.
1) Δ ABC - равнобедренный по условию.
BD - медиана, биссектриса и высота.
Слайд 35Решение.
Δ ABC – равнобедренный
BD - медиана, биссектриса и высота.
3) Δ ABD - прямоугольный т. к. ∠ADB = 90°.
5) BD = AB по свойству катета, лежащего против угла в 30°.
AB = 3 • 2 = 6 см. AB = BC = 6 см.
6) ∠A = ∠C = 30° как углы при основании равнобедренного
треугольника.
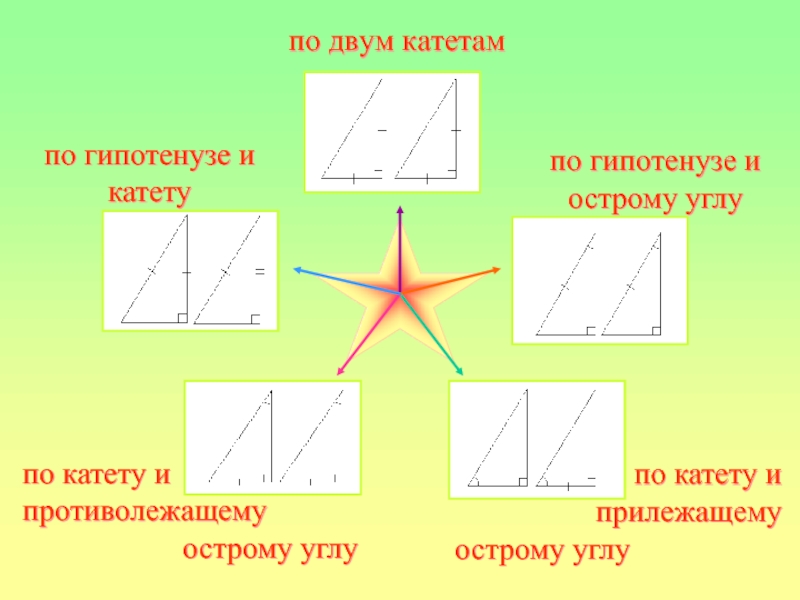
Слайд 36по двум катетам
по гипотенузе и острому углу
по катету и
прилежащему
острому
по катету и
противолежащему
острому углу
по гипотенузе и катету
Слайд 37Докажите, что у равных треугольников высоты, проведенные из соответствующих вершин, равны.
Задача
Доказательство.
2) ΔABD = ΔA1B1D1 по гипотенузе и острому углу.
3) Из равенства треугольников следует BD = B1D1.
Слайд 38Повторение.
№2.
Докажите, что сумма трех внешних углов треугольника, взятых по
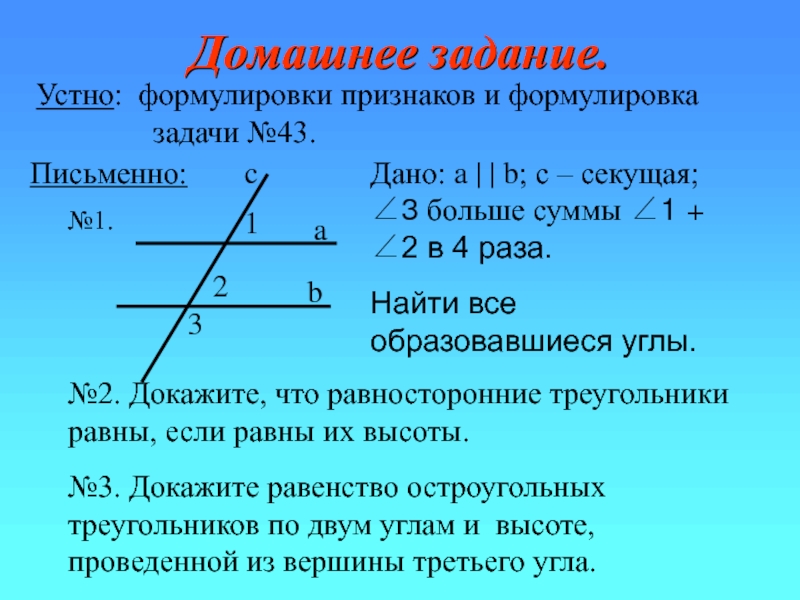
Слайд 39Домашнее задание.
Устно: формулировки признаков и формулировка
№1.
№2. Докажите, что равносторонние треугольники равны, если равны их высоты.
№3. Докажите равенство остроугольных треугольников по двум углам и высоте, проведенной из вершины третьего угла.
Письменно:
1
2
3
a
b
c
Дано: a | | b; с – секущая; ∠3 больше суммы ∠1 + ∠2 в 4 раза.
Найти все образовавшиеся углы.
Слайд 40 BC = AB
Катет,
Свойство катета, лежащего против угла в 30°.