математики БГУИР
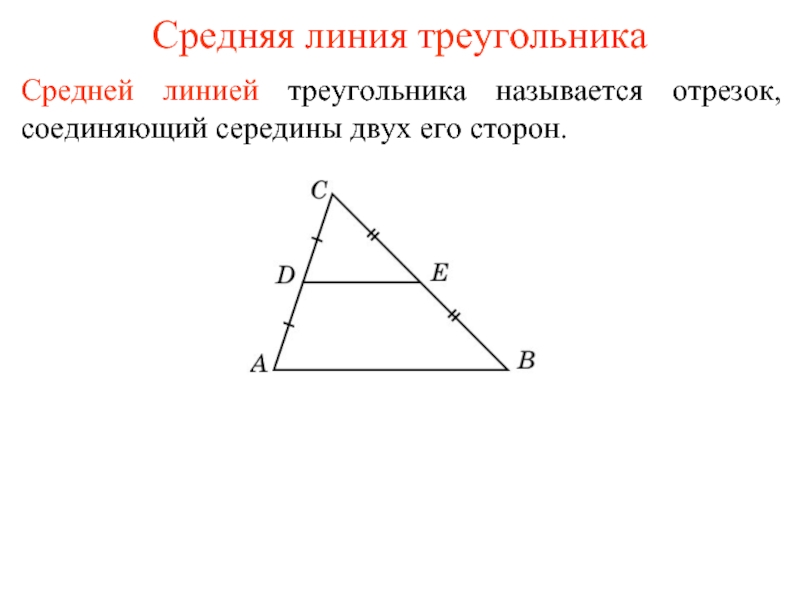
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная функции в точке презентация
Содержание
- 1. Производная функции в точке
- 2. Дифференциальное исчисление Производная обратной функции Пусть
- 3. Дифференциальное исчисление Производная обратной функции Так
- 4. Обратные тригонометрические функции Дифференциальное исчисление Производные
- 5. Обратные тригонометрические функции Дифференциальное исчисление Производные
- 6. Обратные тригонометрические функции Дифференциальное исчисление Производные
- 7. Обратные тригонометрические функции Дифференциальное исчисление Производные
- 8. Дифференциальное исчисление Таблица производных Автор: И.В. Дайняк, к.т.н., доцент Кафедра высшей математики БГУИР
- 9. Дифференциальное исчисление Таблица производных сложной функции
- 10. Дифференциальное исчисление Гиперболические функции 2) гиперболический
- 11. Дифференциальное исчисление Графики гиперболических функций чётная
- 12. Дифференциальное исчисление Гиперболические функции Основные соотношения:
- 13. Дифференциальное исчисление Основные правила дифференцирования (повторение)
- 14. Пусть функция g(x) имеет производную в
- 15. Пример: Решение: Воспользуемся основными правилами дифференцирования:
- 16. Дифференциальное исчисление Логарифмическое дифференцирование Пусть функция
- 17. Пример 1: Решение: Найти производную функции
- 18. Дифференциальное исчисление Логарифмическое дифференцирование Логарифмическое дифференцирование
- 19. Пример 2: Решение: Найти производную функции
- 20. Дифференциальное исчисление Производная функции, заданной параметрически
- 21. Пример: Решение: Найти производную Дифференциальное исчисление
- 22. Дифференциальное исчисление Производная функции, заданной неявно
- 23. Пример: Решение: в точке х0 =
- 24. Высшая математика Автор: И.В. Дайняк, к.т.н., доцент Кафедра высшей математики БГУИР math.mmts-it.org
Дифференциальное исчисление Производная обратной функции Пусть для функции f (x) существует обратная функция f –1. По теореме о производной сложной функции: Имеем: Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей
Слайд 1ПРОИЗВОДНАЯ ФУНКЦИИ
В ТОЧКЕ
Лекция 2
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей
Слайд 2
Дифференциальное исчисление
Производная обратной функции
Пусть для функции f (x) существует обратная функция
f –1.
По теореме о производной сложной функции:
Имеем:
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 3
Дифференциальное исчисление
Производная обратной функции
Так как
то
Отсюда:
или
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей
математики БГУИР
Слайд 4
Обратные тригонометрические функции
Дифференциальное исчисление
Производные элементарных функций
Имеем:
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра
высшей математики БГУИР
Слайд 5
Обратные тригонометрические функции
Дифференциальное исчисление
Производные элементарных функций
Имеем:
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра
высшей математики БГУИР
Слайд 6
Обратные тригонометрические функции
Дифференциальное исчисление
Производные элементарных функций
Имеем:
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра
высшей математики БГУИР
Слайд 7
Обратные тригонометрические функции
Дифференциальное исчисление
Производные элементарных функций
Имеем:
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра
высшей математики БГУИР
Слайд 8
Дифференциальное исчисление
Таблица производных
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 9
Дифференциальное исчисление
Таблица производных сложной функции
Пусть
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей
математики БГУИР
Слайд 10
Дифференциальное исчисление
Гиперболические функции
2) гиперболический синус
3) гиперболический тангенс
4) гиперболический котангенс
1) гиперболический косинус
Автор:
И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 11
Дифференциальное исчисление
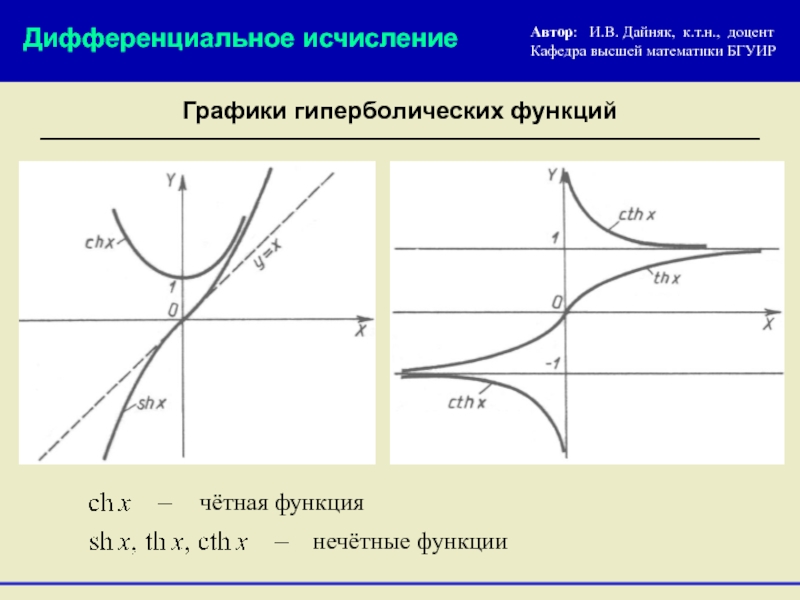
Графики гиперболических функций
чётная функция
нечётные функции
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра
высшей математики БГУИР
Слайд 12
Дифференциальное исчисление
Гиперболические функции
Основные соотношения:
Производные:
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики
БГУИР
Слайд 13
Дифференциальное исчисление
Основные правила дифференцирования (повторение)
2) формула производной суммы
3) формула производной произведения
4)
формула производной частного
1) константу можно выносить за знак производной
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 14
Пусть функция g(x) имеет производную в точке x0, а функция f
(y) имеет производную в точке y0 = g(x0). Тогда сложная функция f (g(x)) имеет производную в точке x0, вычисляемую по формуле
Дифференциальное исчисление
Производная сложной функции (повторение)
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 15
Пример:
Решение:
Воспользуемся основными правилами дифференцирования:
Найти производную функции
Дифференциальное исчисление
Нахождение производной функции
Автор: И.В.
Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 16
Дифференциальное исчисление
Логарифмическое дифференцирование
Пусть функция f (x) > 0.
По теореме о производной
сложной функции:
Выразим отсюда производную:
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 17
Пример 1:
Решение:
Найти производную функции
Дифференциальное исчисление
Логарифмическое дифференцирование
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра
высшей математики БГУИР
Слайд 18
Дифференциальное исчисление
Логарифмическое дифференцирование
Логарифмическое дифференцирование применяется для нахождения производной сложной функции вида
представляющей
собой «функцию в степени функция».
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 19
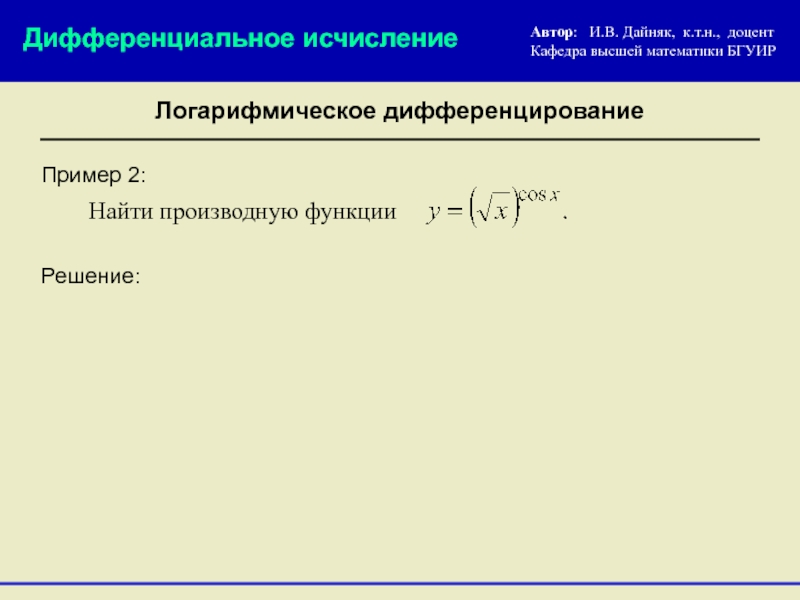
Пример 2:
Решение:
Найти производную функции
Дифференциальное исчисление
Логарифмическое дифференцирование
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра
высшей математики БГУИР
Слайд 20
Дифференциальное исчисление
Производная функции, заданной параметрически
Пусть функция у переменной х задана параметрически:
Предположим,
что функция x = x (t) имеет обратную функцию
t = t (x), определённую в некоторой окрестности точки x0 = x (t0), а также существуют производные x’(t0) и y’(t0).
t = t (x), определённую в некоторой окрестности точки x0 = x (t0), а также существуют производные x’(t0) и y’(t0).
где функции ϕ(t), ψ(t) определены в некоторой окрестности точки t0.
Тогда:
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 21
Пример:
Решение:
Найти производную
Дифференциальное исчисление
Производная функции, заданной параметрически
функции, заданной уравнениями
Автор: И.В. Дайняк,
к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 22
Дифференциальное исчисление
Производная функции, заданной неявно
1. Дифференцируем тождество по переменной х как
сложную функцию, предполагая, что у = f (х).
Пусть функция у переменной х задана неявно уравнением
2. Из полученного уравнения пытаемся выразить у’х = f‘ (х).
Для нахождения у’х :
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 23
Пример:
Решение:
в точке х0 = 0.
Найти производную неявной функции, заданной уравнением
Дифференциальное исчисление
Производная
функции, заданной неявно
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 24
Высшая математика
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
math.mmts-it.org
