- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обобщающие таблицы по геометрии. Треугольники, четырехугольники,, окружность, площади фигур, векторы движения презентация
Содержание
- 1. Обобщающие таблицы по геометрии. Треугольники, четырехугольники,, окружность, площади фигур, векторы движения
- 2. ТРЕУГОЛЬНИКИ Виды треугольников Признаки равенства
- 3. Виды треугольников по углам
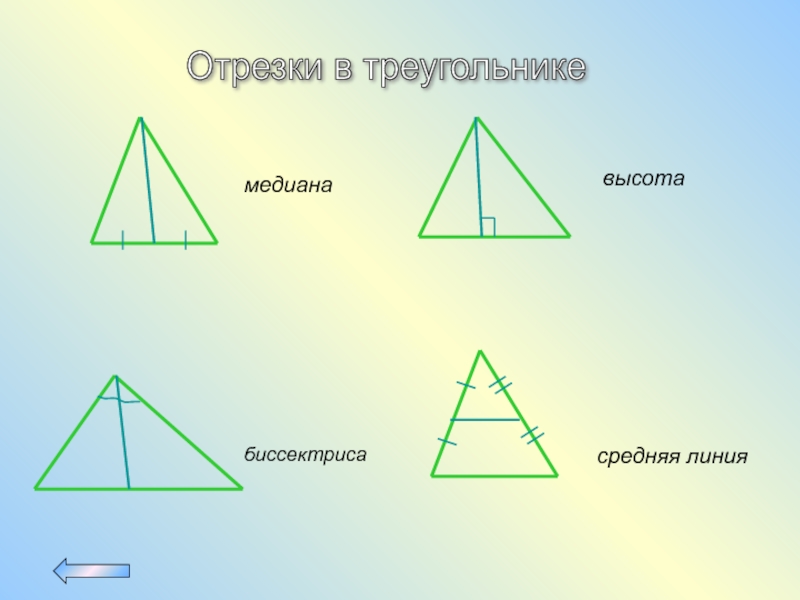
- 4. Отрезки в треугольнике медиана высота биссектриса средняя линия
- 5. Соотношения между сторонами и углами треугольника
- 6. Признаки равенства треугольников По двум сторонам
- 7. ПОДОБИЕ ТРЕУГОЛЬНИКОВ Определение Свойства Признаки подобия
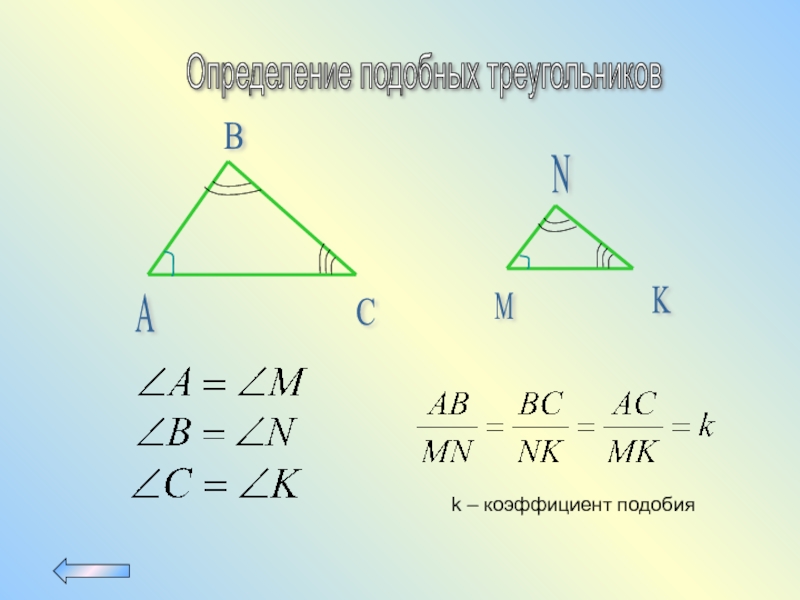
- 8. Определение подобных треугольников C A
- 9. Признаки подобных треугольников C A
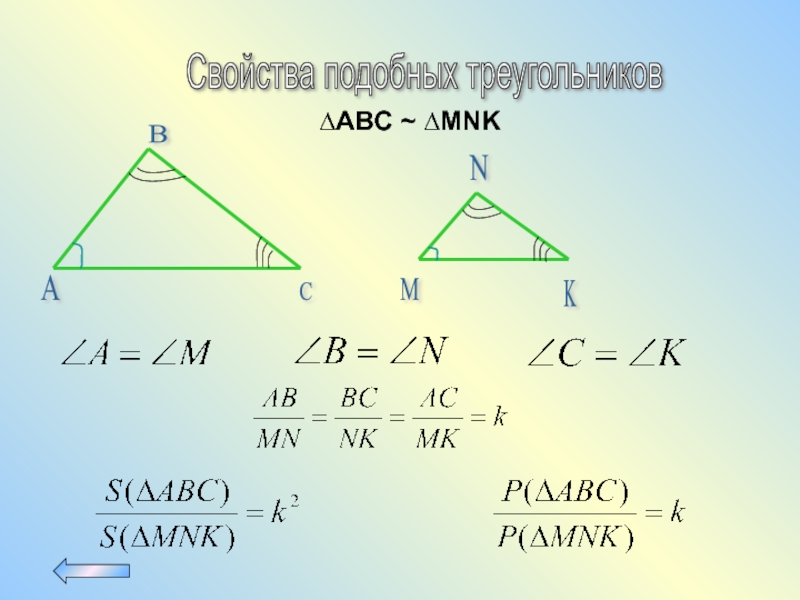
- 10. Свойства подобных треугольников A B
- 11. ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК Признаки равенства Соотношения
- 12. Признаки равенства прямоугольных треугольников По катету
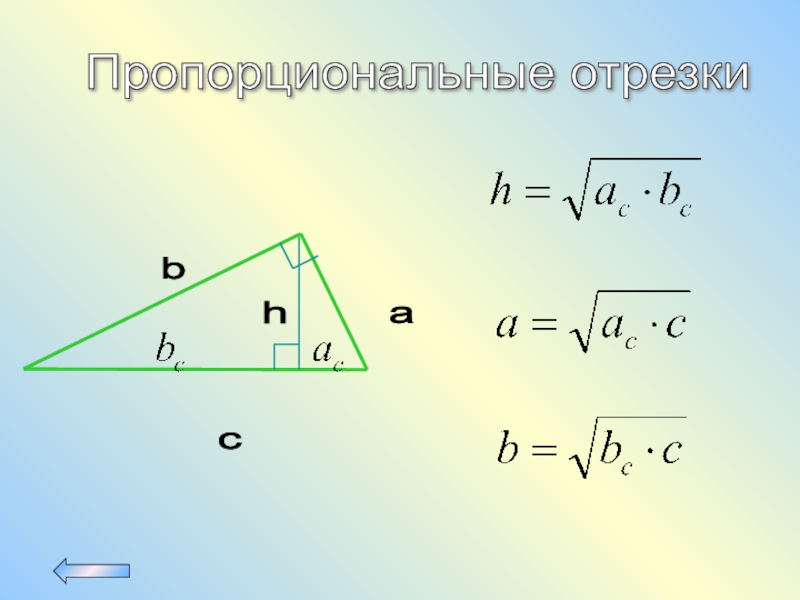
- 13. Пропорциональные отрезки a b c h
- 14. Соотношения между сторонами и углами a
- 15. РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК Определение Признаки Свойства
- 16. Определение Если две стороны треугольника равны, то он равнобедренный
- 17. Свойства равноберенного треугольника Углы при
- 18. Признаки равноберенного треугольника Если в
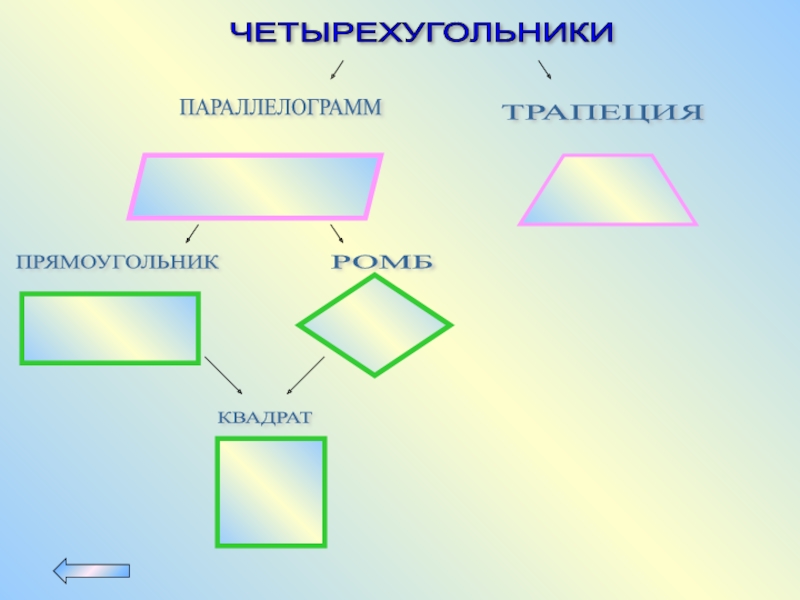
- 19. ЧЕТЫРЕХУГОЛЬНИКИ ПАРАЛЛЕЛОГРАММ
- 20. ПАРАЛЛЕЛОГРАММ Определение Свойства Признаки
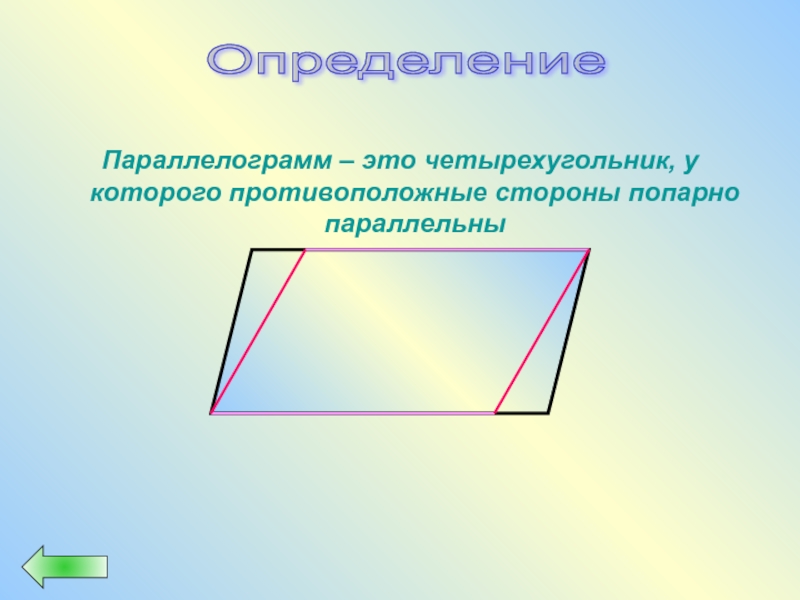
- 21. Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны Определение
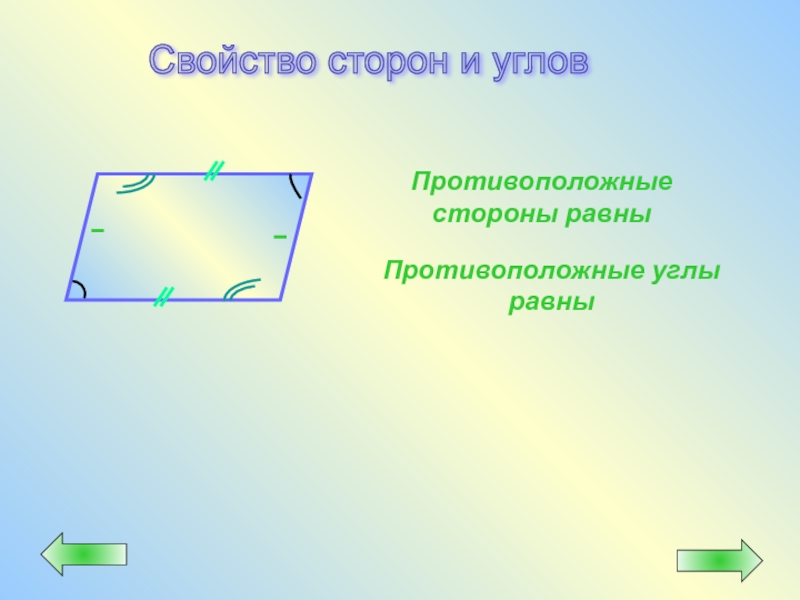
- 22. Противоположные стороны равны Противоположные углы равны Свойство сторон и углов
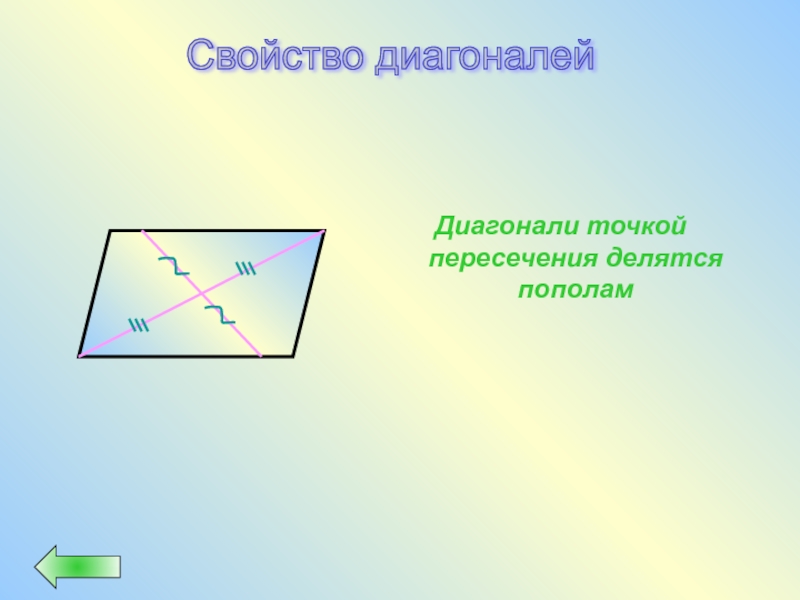
- 23. Диагонали точкой пересечения делятся пополам Свойство диагоналей
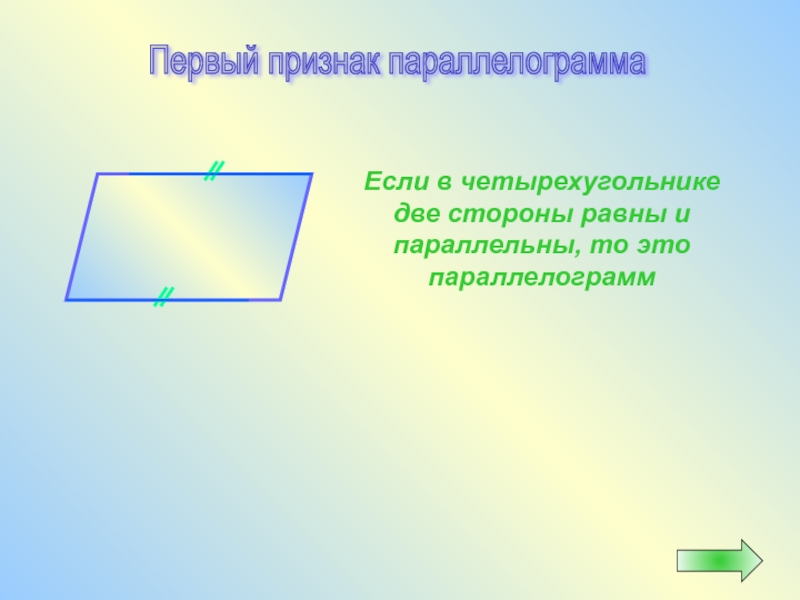
- 24. Если в четырехугольнике две стороны равны
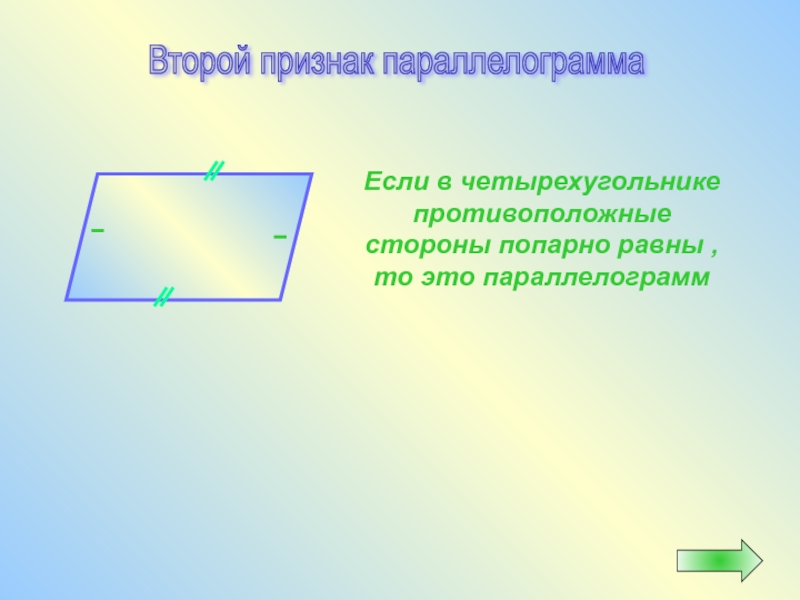
- 25. Если в четырехугольнике противоположные стороны попарно
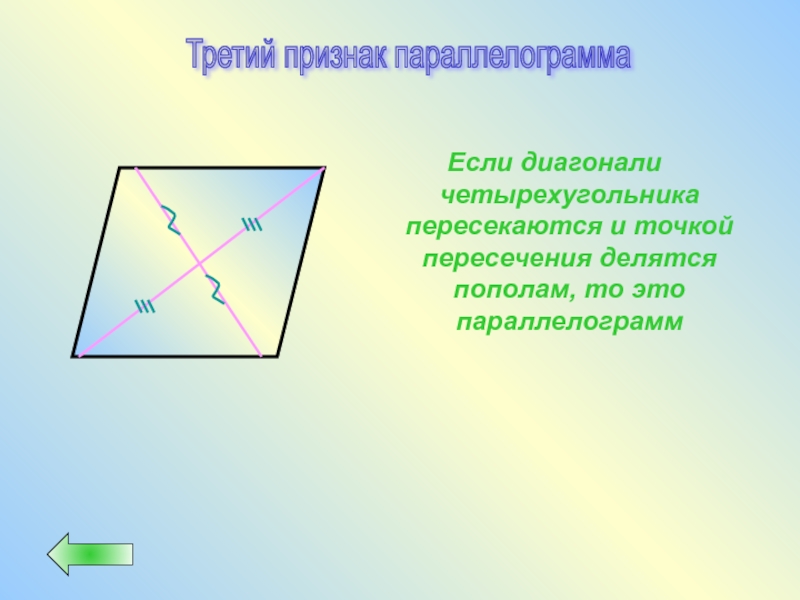
- 26. Если диагонали четырехугольника пересекаются и точкой пересечения
- 27. ПРЯМОУГОЛЬНИК Определение Свойства Признак
- 28. Прямоугольник – это параллелограмм, у которого все углы прямые Определение
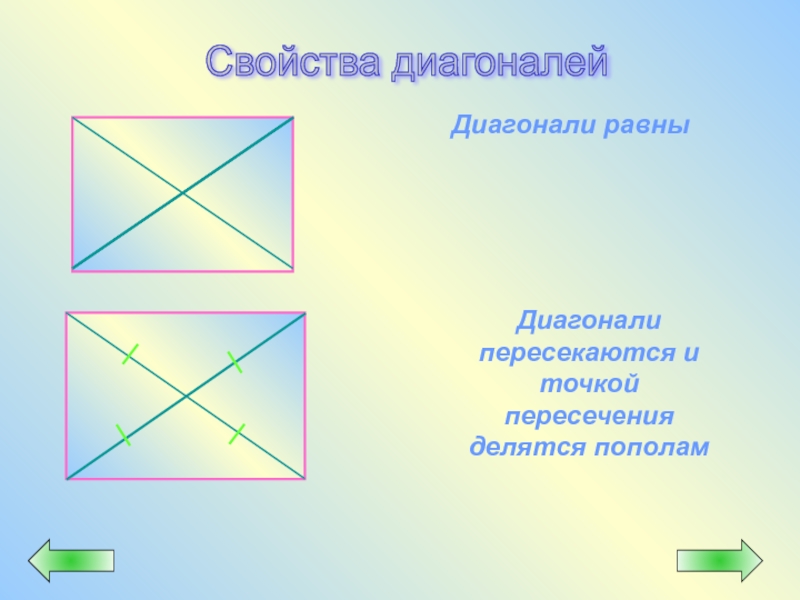
- 29. Свойства диагоналей Диагонали равны Диагонали пересекаются
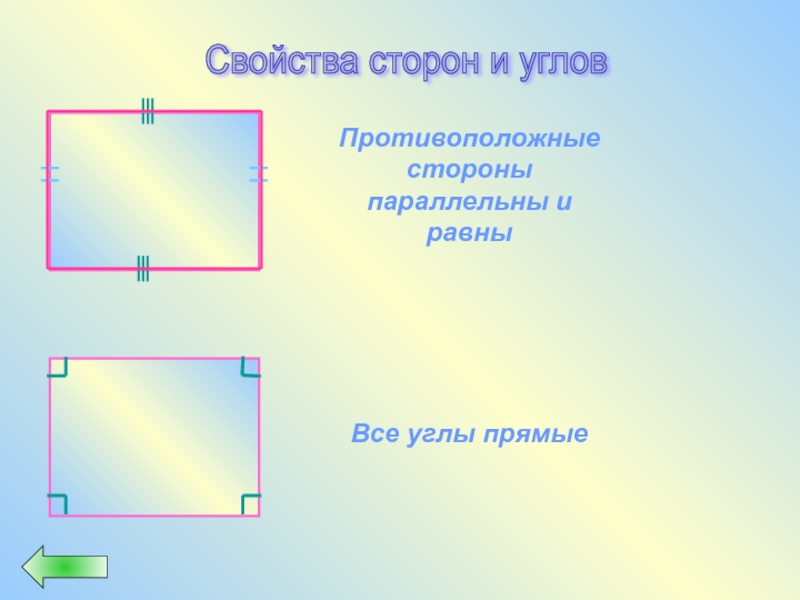
- 30. Свойства сторон и углов
- 31. Признак прямоугольника Если в параллелограмме диагонали равны, то это прямоугольник
- 32. РОМБ Определение Свойства Признак
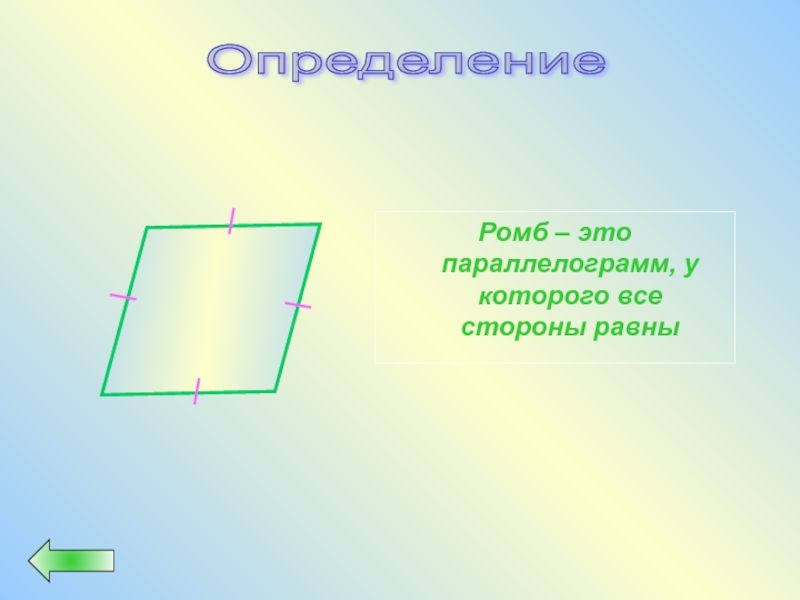
- 33. Ромб – это параллелограмм, у которого все стороны равны Определение
- 34. Признак ромба Если диагонали параллелограмма
- 35. Свойства сторон и углов Противоположные стороны
- 36. Свойства диагоналей Диагонали пересекаются и точкой
- 37. КВАДРАТ Определение Свойства Признаки
- 38. Квадрат – это прямоугольник, у которого все
- 39. Признаки квадрата Если в
- 40. Свойства диагоналей Диагонали взаимно перпендикулярны и
- 41. Свойства сторон и углов Все углы
- 42. ТРАПЕЦИЯ Определение Виды трапеций
- 43. Определение Четырехугольник, у которого две стороны
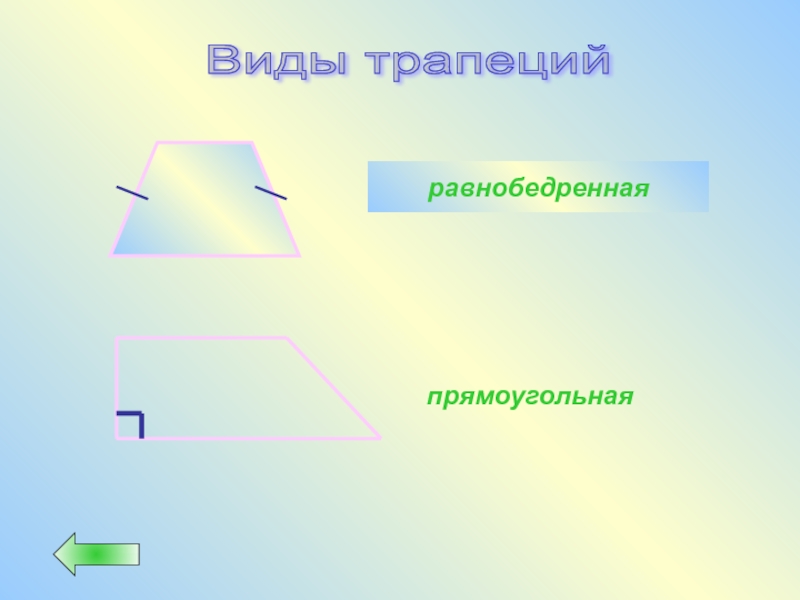
- 44. Виды трапеций равнобедренная прямоугольная
- 45. РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ Свойства Определение
- 46. Определение Трапеция, у которой боковые стороны равны, называется равнобедренной (равнобокой) трапецией
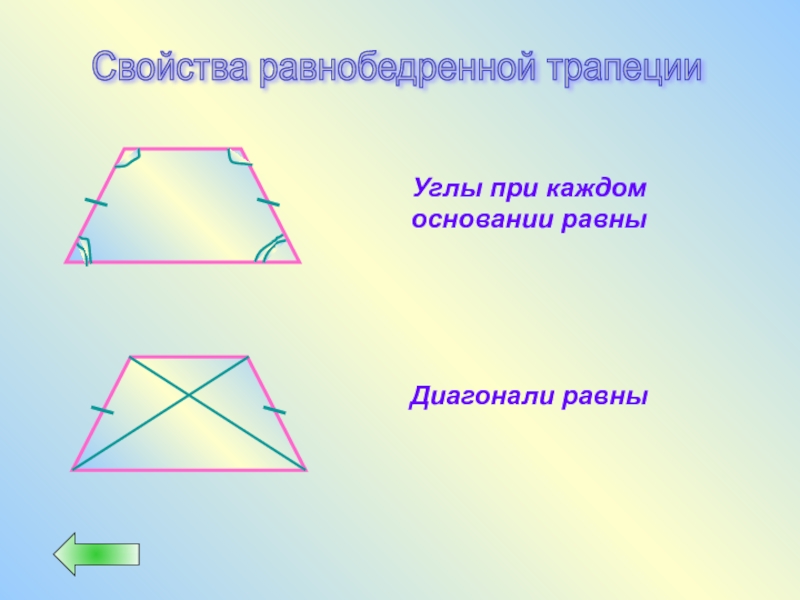
- 47. Свойства равнобедренной трапеции Углы при каждом основании равны Диагонали равны
- 48. ПЛОЩАДИ ФИГУР Треугольники Четырехугольники Круг
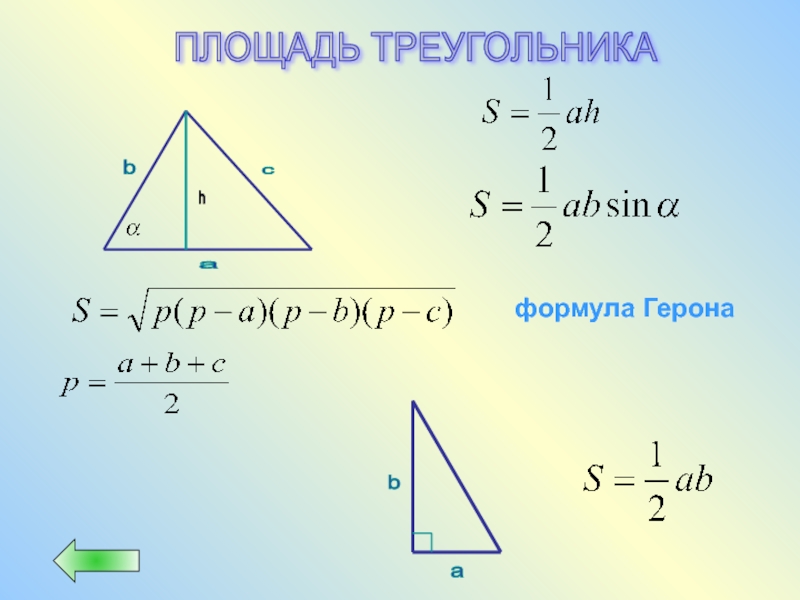
- 49. ПЛОЩАДЬ ТРЕУГОЛЬНИКА b c
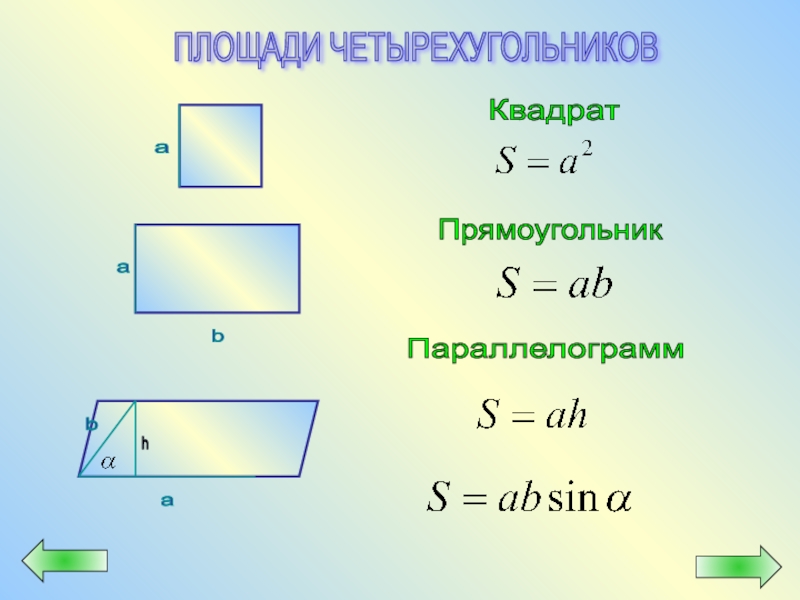
- 50. ПЛОЩАДИ ЧЕТЫРЕХУГОЛЬНИКОВ Квадрат
- 51. ПЛОЩАДИ ЧЕТЫРЕХУГОЛЬНИКОВ b a Ромб Трапеция
- 52. ПЛОЩАДЬ КРУГА r
- 53. Окружность Взаимное расположение прямой и окружности
- 54. Взаимное расположение прямой и окружности
- 55. Касательная к окружности Свойство касательной
- 56. Свойство касательной A B
- 57. A B H О
- 58. Свойства отрезков касательных, секущих и хорд
- 59. Углы в окружности A B
- 60. Вписанные и описанные многоугольники Треугольник Четырехугольник
- 61. Вписанные и описанные треугольники A
- 62. Вписанные и описанные четырехугольники A
- 63. Векторы на плоскости Вектор и его
- 64. Вектор и его координаты Вектор – это направленный отрезок
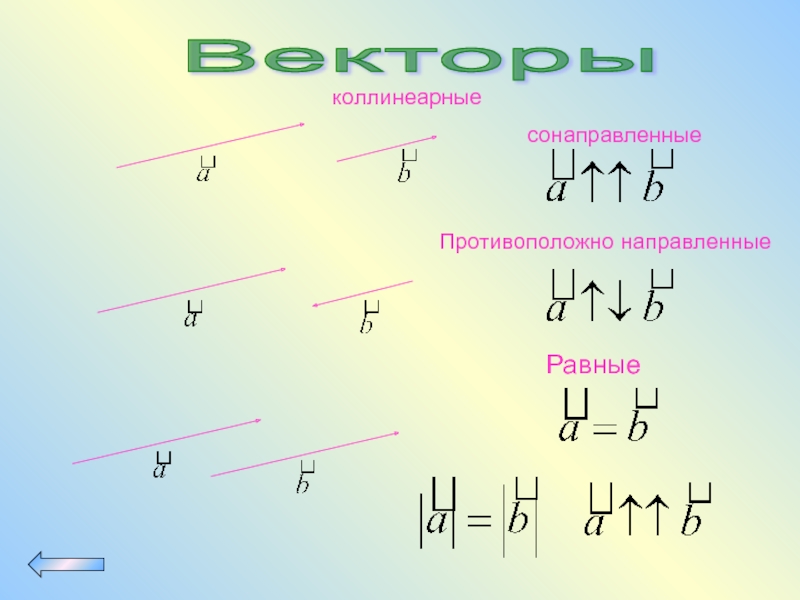
- 65. Векторы сонаправленные Противоположно направленные коллинеарные Равные
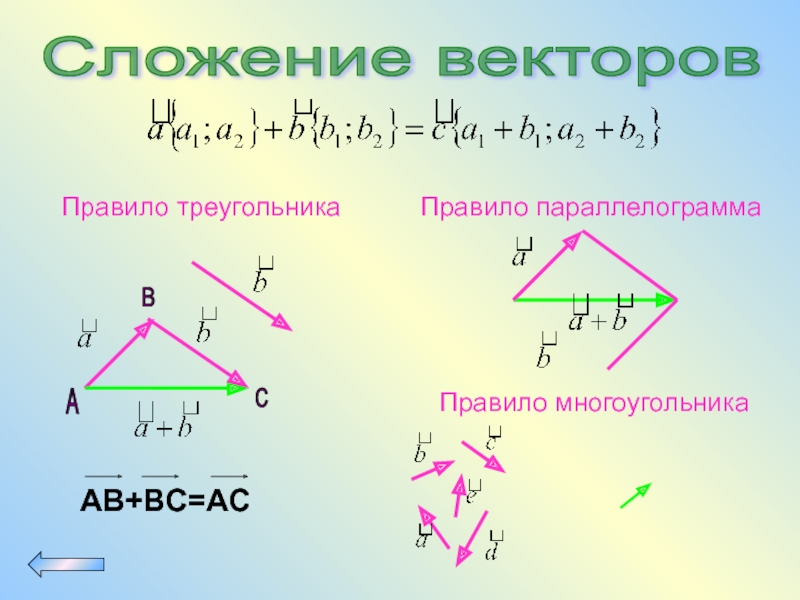
- 66. Сложение векторов А B
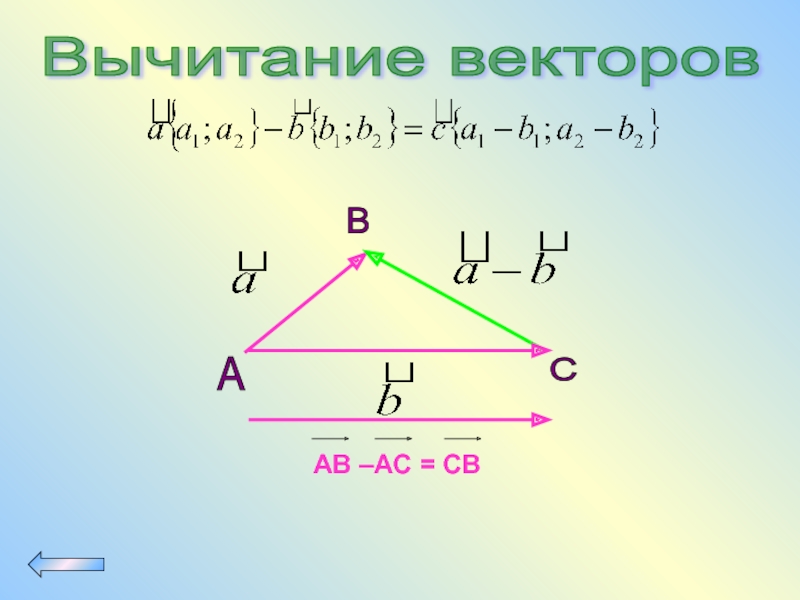
- 67. Вычитание векторов А B C
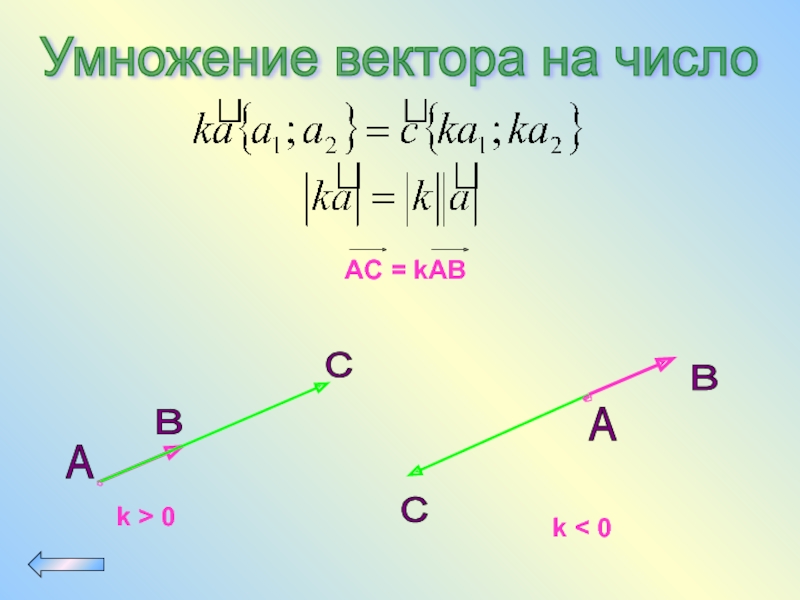
- 68. Умножение вектора на число А
- 69. Скалярное произведение векторов
- 70. Движения Свойства движений Центральная
- 71. Свойства движений Движение – отображение плоскости
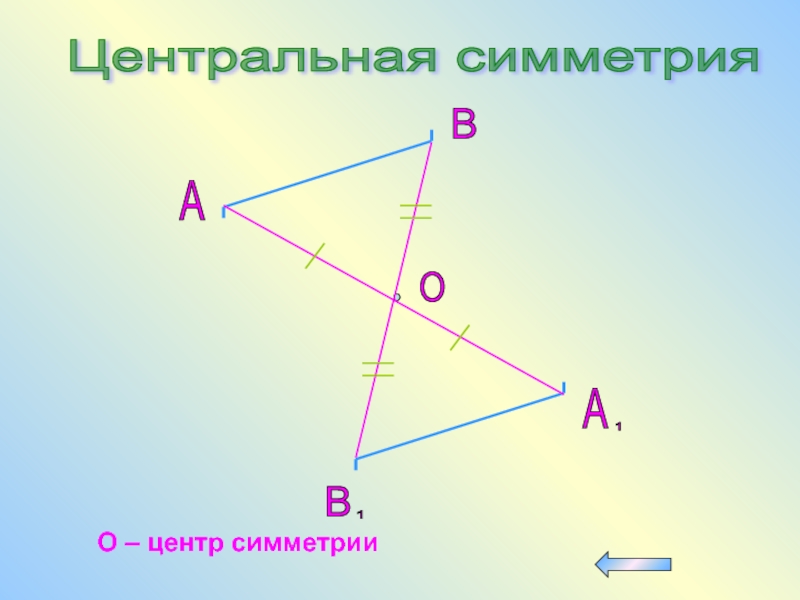
- 72. Центральная симметрия A B O О – центр симметрии
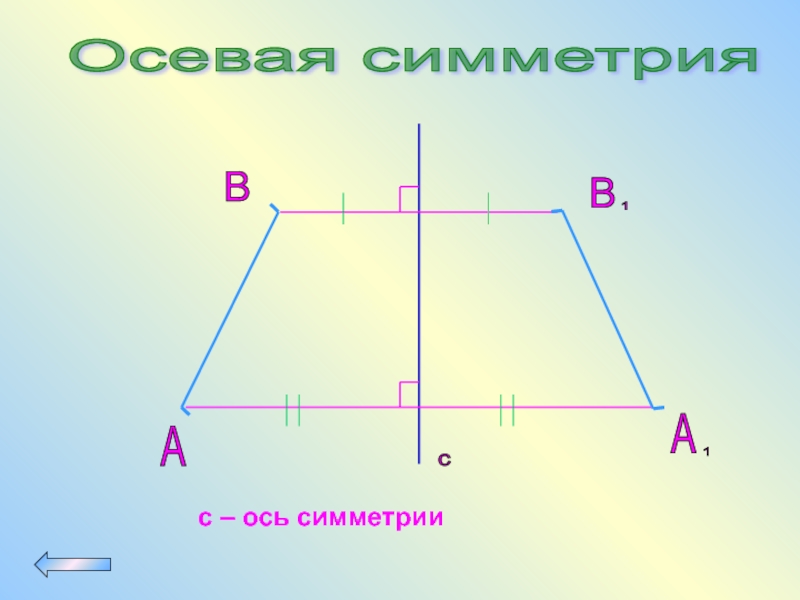
- 73. Осевая симметрия A B c с – ось симметрии
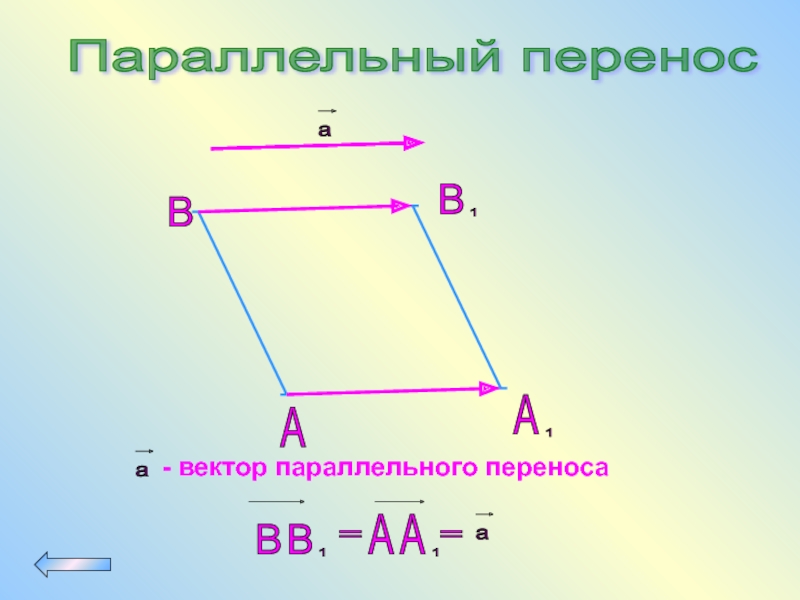
- 74. Параллельный перенос A B
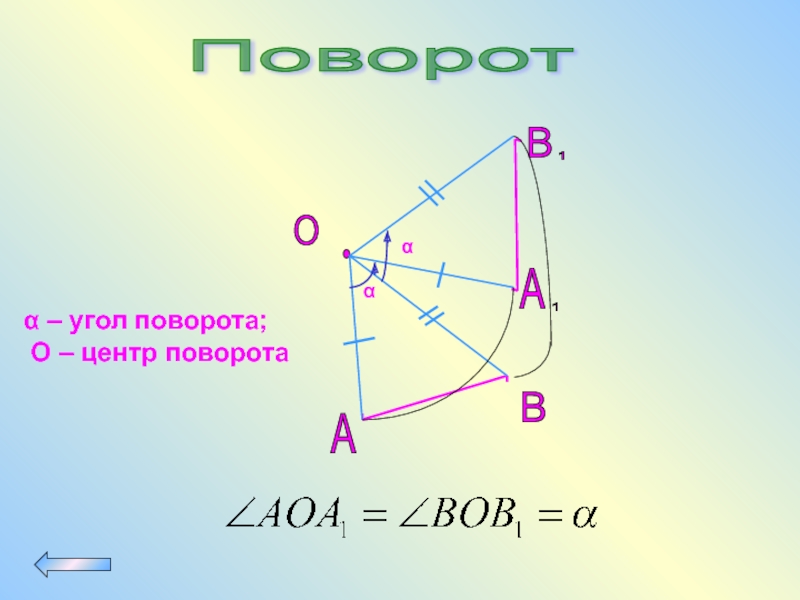
- 75. Поворот α – угол поворота;
ТРЕУГОЛЬНИКИ Виды треугольников Признаки равенства Подобие треугольников Соотношения между сторонами и углами Площадь Отрезки в треугольнике
Слайд 1ОБОБЩАЮЩИЕ ТАБЛИЦЫ ПО ГЕОМЕТРИИ
ТРЕУГОЛЬНИКИ
ЧЕТЫРЕХУГОЛЬНИКИ
ПЛОЩАДИ ФИГУР
ОКРУЖНОСТЬ
ВЕКТОРЫ
ДВИЖЕНИЯ
Слайд 2ТРЕУГОЛЬНИКИ
Виды треугольников
Признаки равенства
Подобие треугольников
Соотношения между сторонами и
углами
Площадь
Отрезки в треугольнике
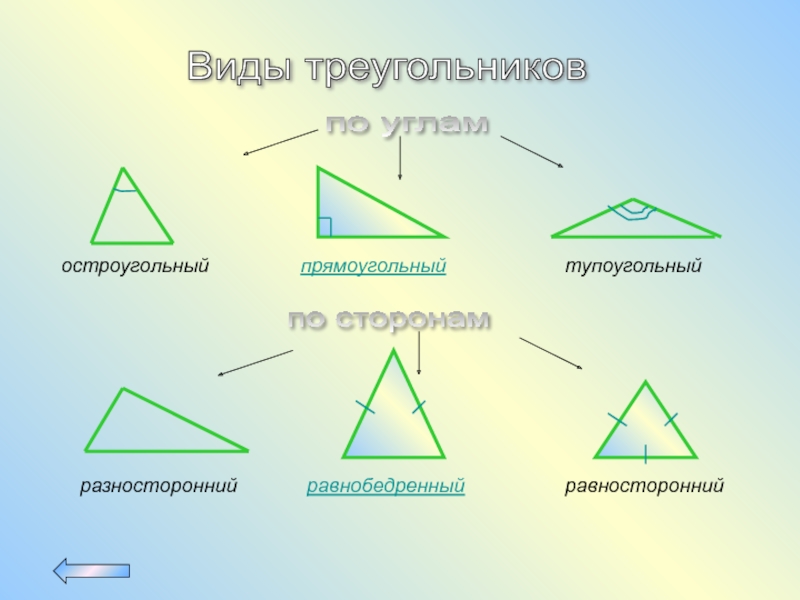
Слайд 3Виды треугольников
по углам
остроугольный
прямоугольный
тупоугольный
по сторонам
разносторонний
равнобедренный
равносторонний
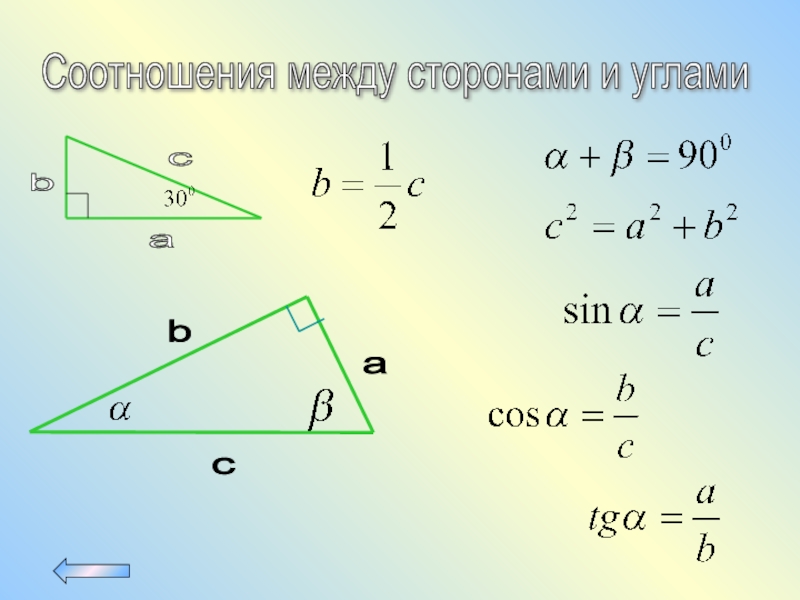
Слайд 5Соотношения между сторонами и углами треугольника
А
В
С
а
с
b
Теорема синусов
Теорема косинусов
Неравенство треугольника
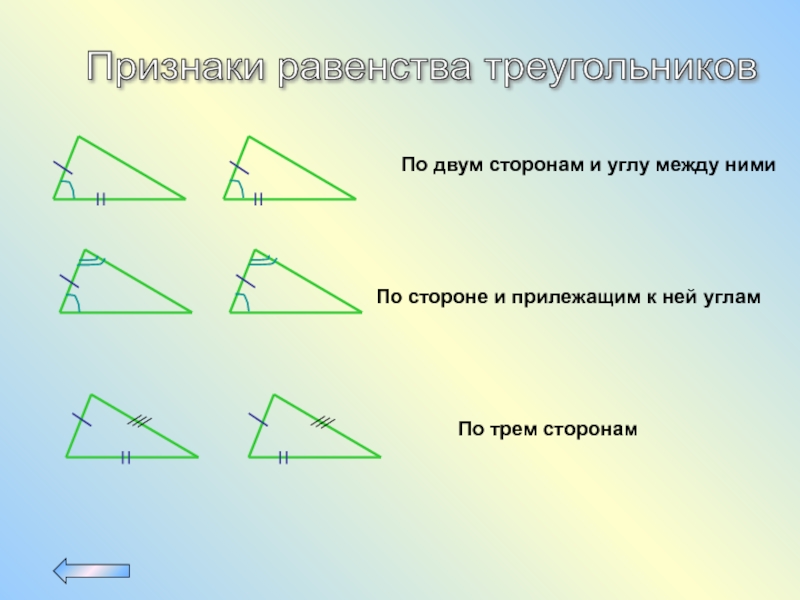
Слайд 6Признаки равенства треугольников
По двум сторонам и углу между ними
По трем
сторонам
По стороне и прилежащим к ней углам
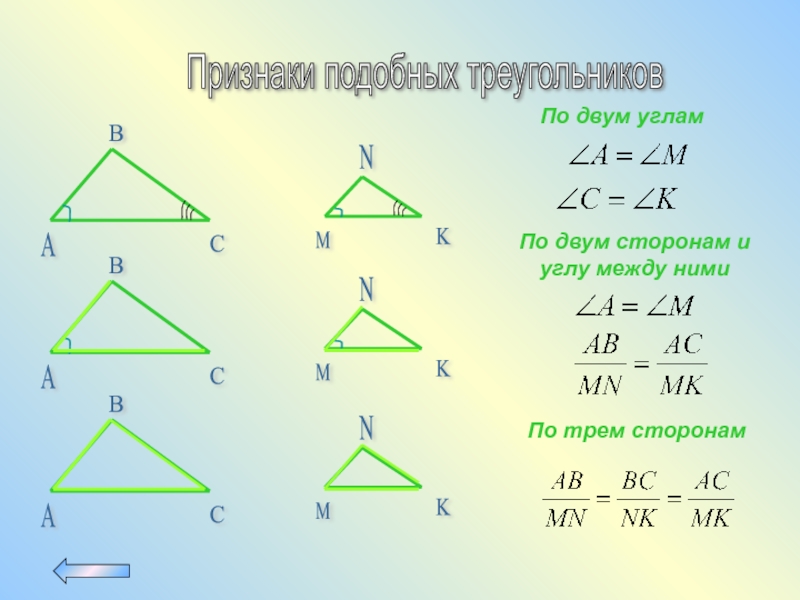
Слайд 9Признаки подобных треугольников
C
A
B
N
K
M
C
A
B
N
K
M
C
A
B
N
K
M
По двум углам
По двум сторонам и углу между ними
По трем сторонам
Слайд 11ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Признаки равенства
Соотношения между сторонами и углами
Пропорциональные отрезки
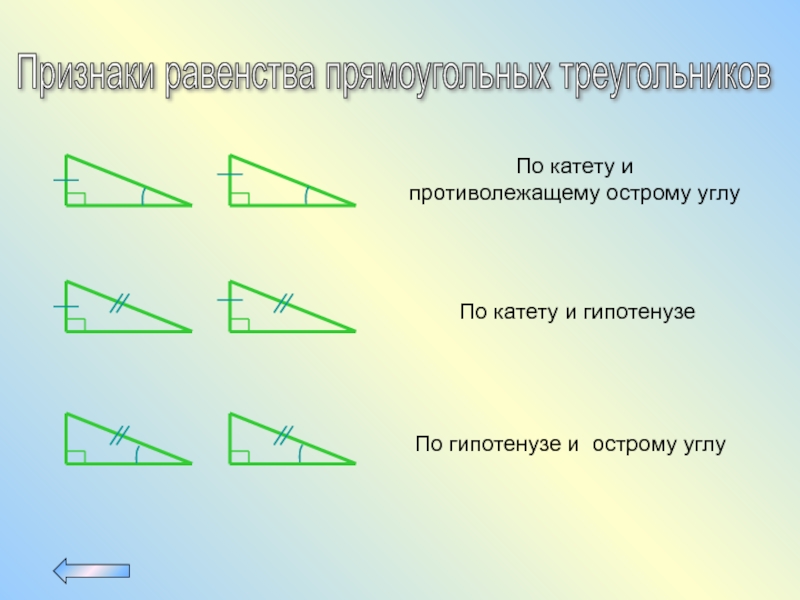
Слайд 12Признаки равенства прямоугольных треугольников
По катету и
противолежащему острому углу
По катету
и гипотенузе
По гипотенузе и острому углу
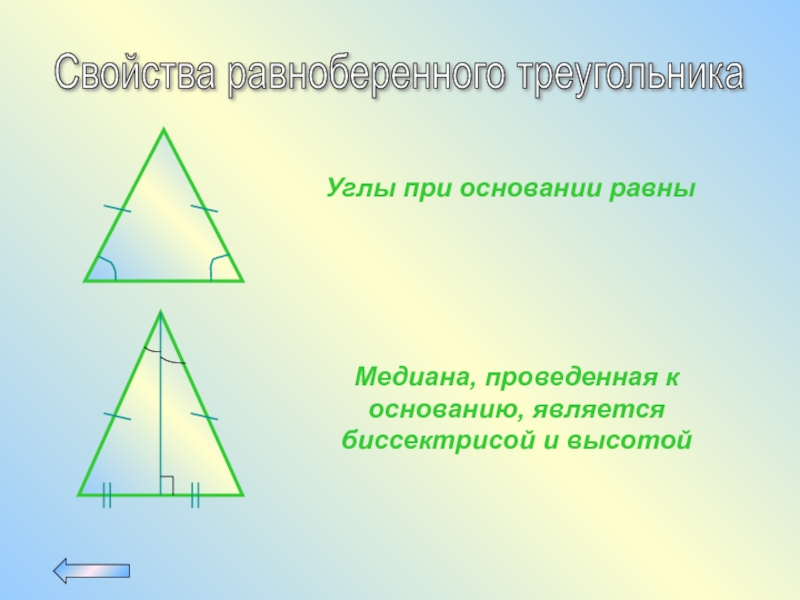
Слайд 17Свойства равноберенного треугольника
Углы при основании равны
Медиана, проведенная к основанию, является
биссектрисой и высотой
Слайд 18Признаки равноберенного треугольника
Если в треугольнике два угла равны, то он
равнобедренный
Если медиана является высотой, то треугольник равнобедренный
Если медиана является биссектрисой, то треугольник равнобедренный
Если биссектриса является высотой, то треугольник равнобедренный
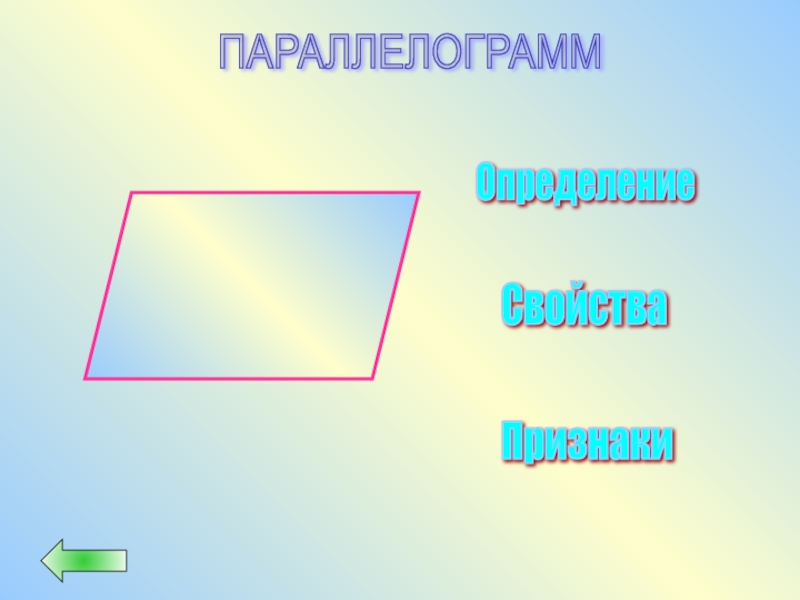
Слайд 21Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны
Определение
Слайд 24
Если в четырехугольнике две стороны равны и параллельны, то это параллелограмм
Первый
признак параллелограмма
Слайд 25
Если в четырехугольнике противоположные стороны попарно равны , то это параллелограмм
Второй
признак параллелограмма
Слайд 26Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то это
параллелограмм
Третий признак параллелограмма
Слайд 29Свойства диагоналей
Диагонали равны
Диагонали пересекаются и точкой пересечения делятся пополам
Слайд 34Признак ромба
Если диагонали параллелограмма взаимно перпендикулярны и являются биссектрисами углов,
то это ромб
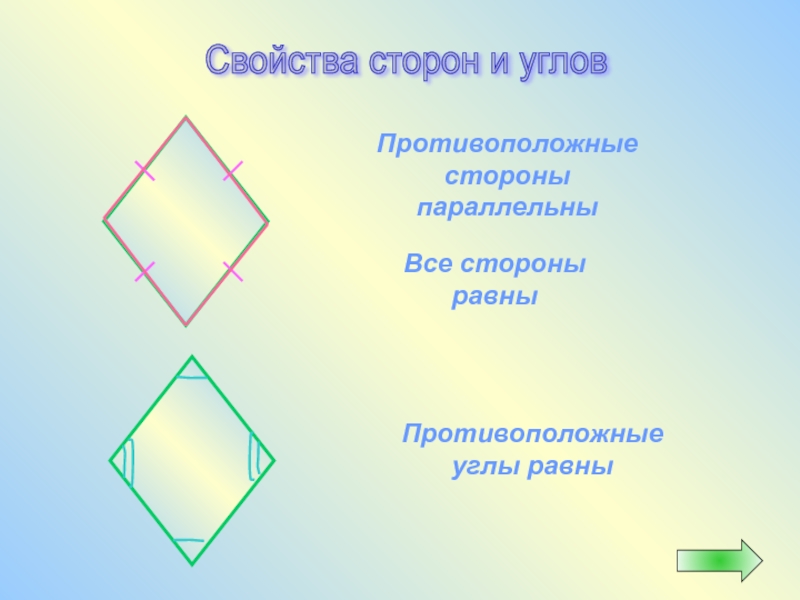
Слайд 35Свойства сторон и углов
Противоположные стороны параллельны
Противоположные углы равны
Все стороны
равны
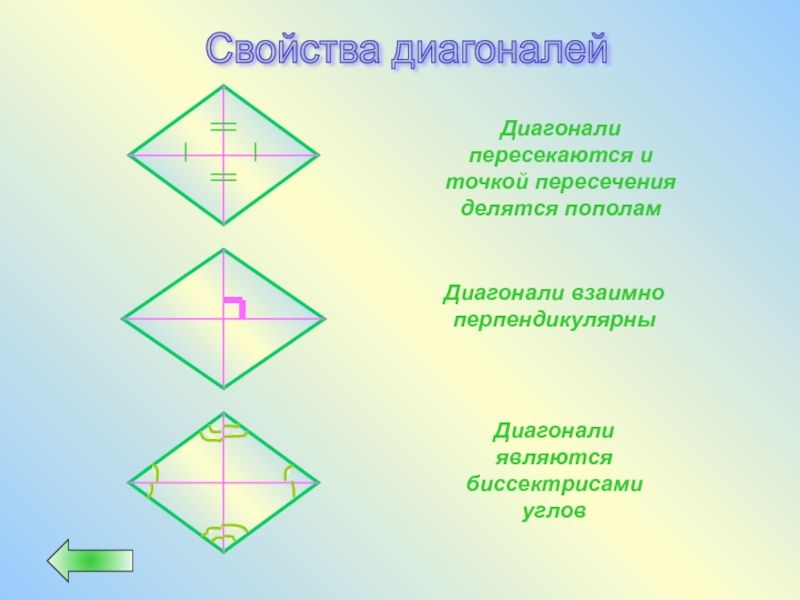
Слайд 36Свойства диагоналей
Диагонали пересекаются и точкой пересечения делятся пополам
Диагонали взаимно перпендикулярны
Диагонали
являются биссектрисами углов
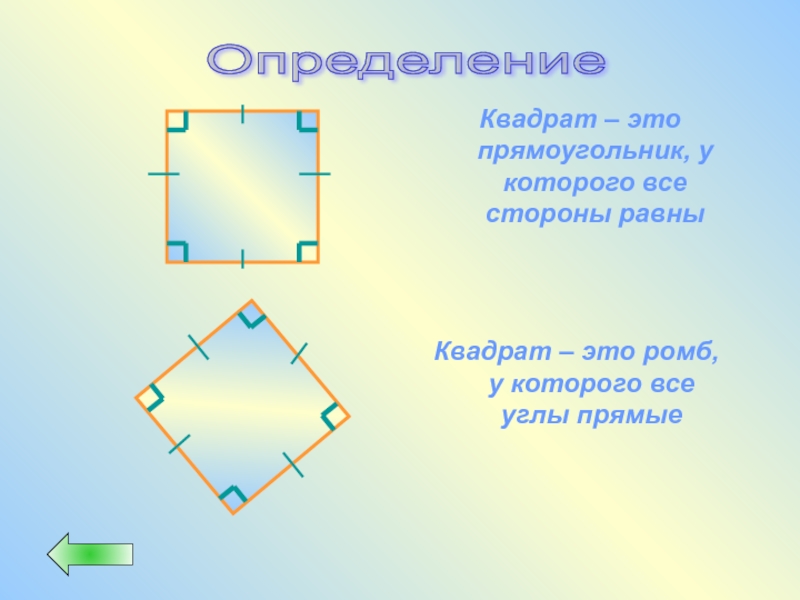
Слайд 38Квадрат – это прямоугольник, у которого все стороны равны
Определение
Квадрат –
это ромб, у которого все углы прямые
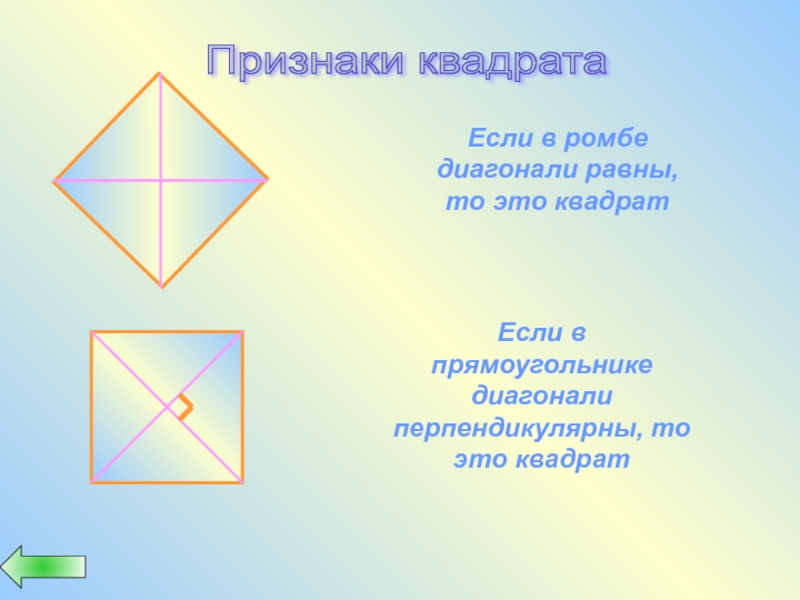
Слайд 39Признаки квадрата
Если в ромбе диагонали равны, то это квадрат
Если в
прямоугольнике диагонали перпендикулярны, то это квадрат
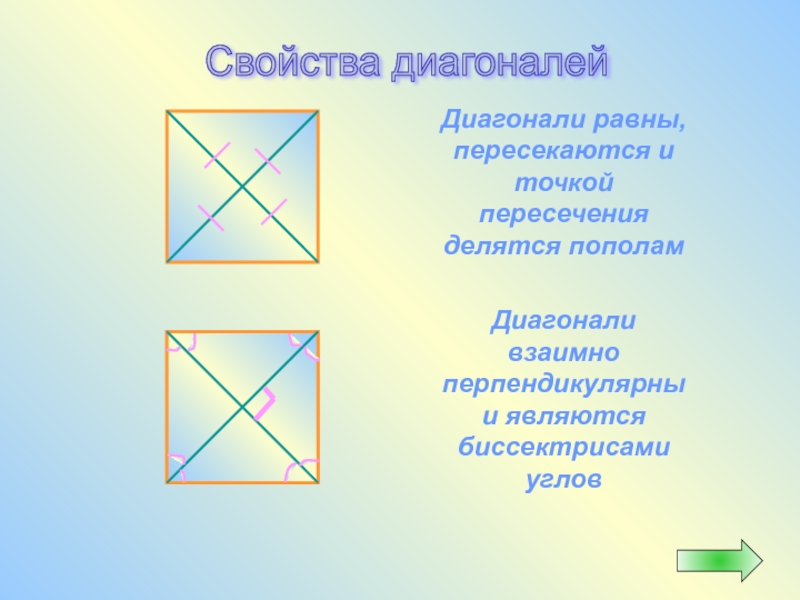
Слайд 40Свойства диагоналей
Диагонали взаимно перпендикулярны и являются биссектрисами углов
Диагонали равны,
пересекаются и
точкой пересечения делятся пополам
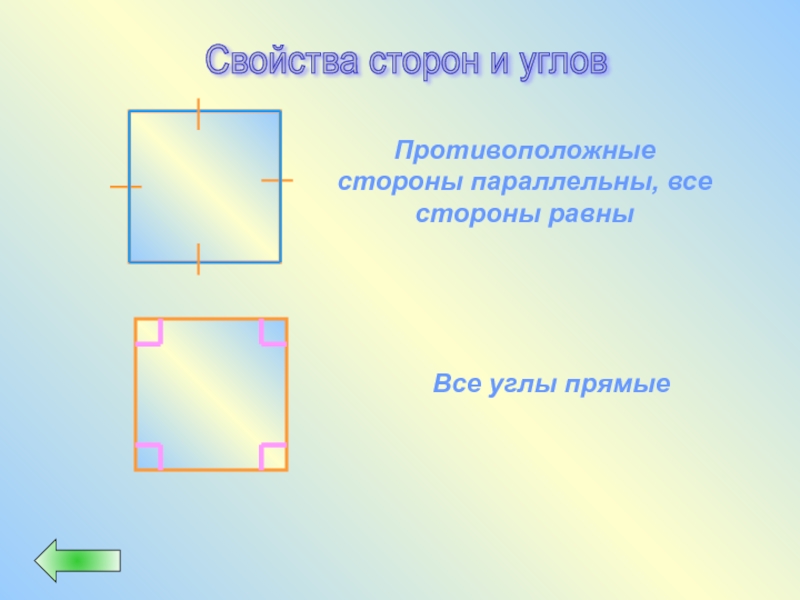
Слайд 41Свойства сторон и углов
Все углы прямые
Противоположные стороны параллельны, все стороны
равны
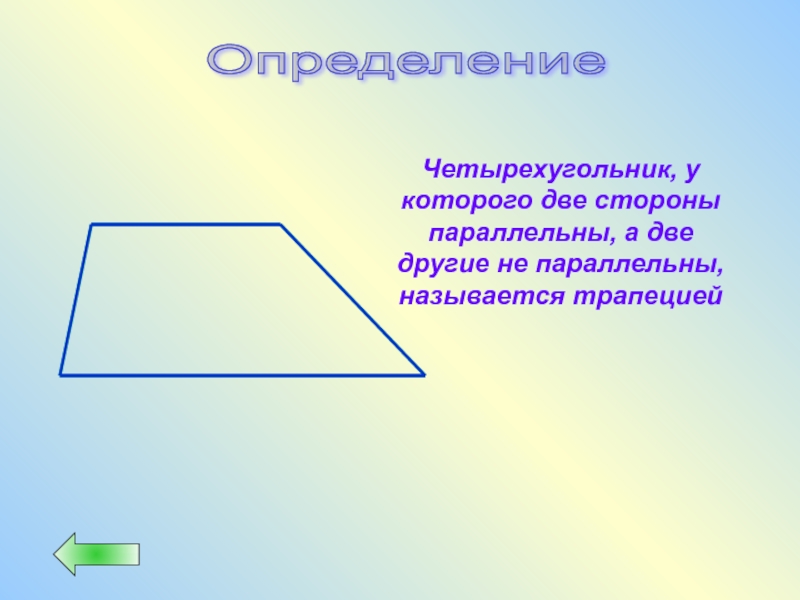
Слайд 43Определение
Четырехугольник, у которого две стороны параллельны, а две другие не
параллельны, называется трапецией
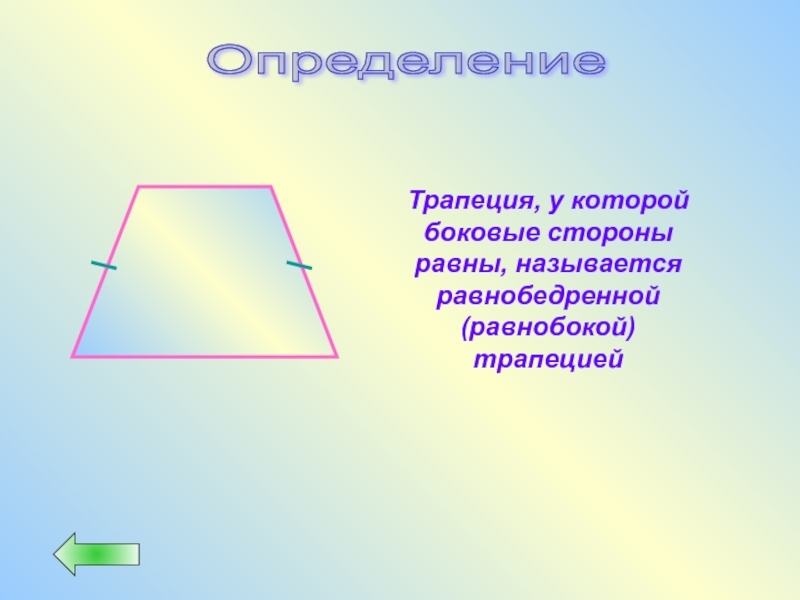
Слайд 46Определение
Трапеция, у которой боковые стороны равны, называется равнобедренной (равнобокой) трапецией
Слайд 53Окружность
Взаимное расположение прямой и окружности
Вписанные и описанные многоугольники
Углы
в окружности
Касательная к окружности
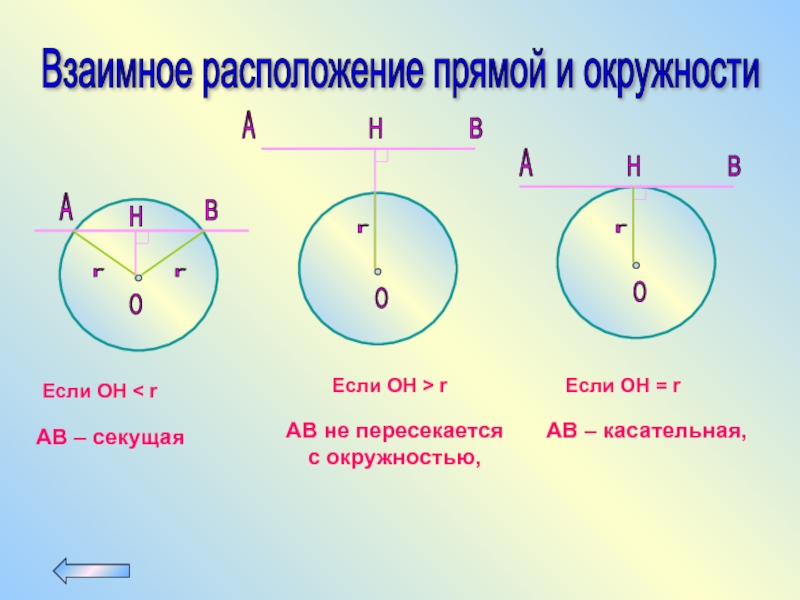
Слайд 54Взаимное расположение прямой и окружности
A
B
О
H
r
r
A
B
H
О
r
A
B
H
О
r
AB – секущая
AB не пересекается
с окружностью,
AB – касательная,
Если OH < r
Если OH > r
Если OH = r
Слайд 55Касательная к окружности
Свойство касательной
Признак касательной
Свойства отрезков хорд, секущих
и касательных
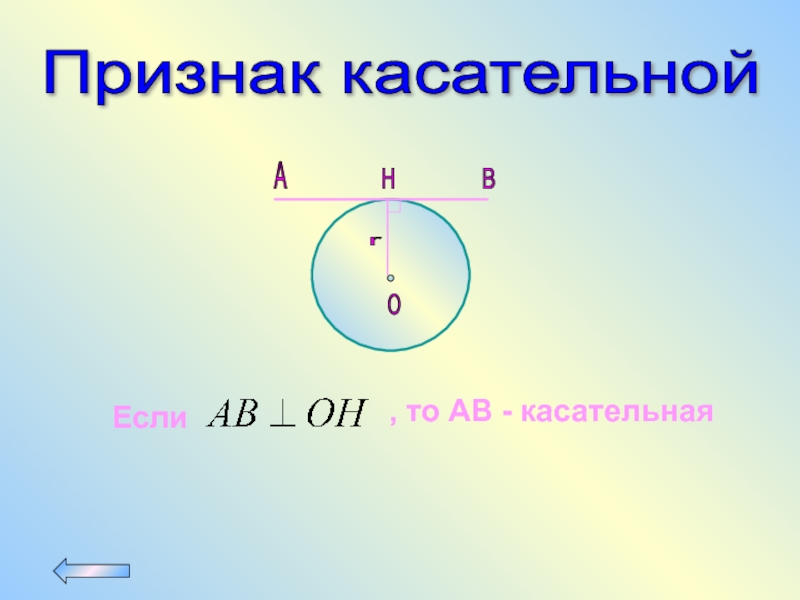
Слайд 56Свойство касательной
A
B
H
О
r
Касательная перпендикулярна радиусу,
проведенному
в точку касания
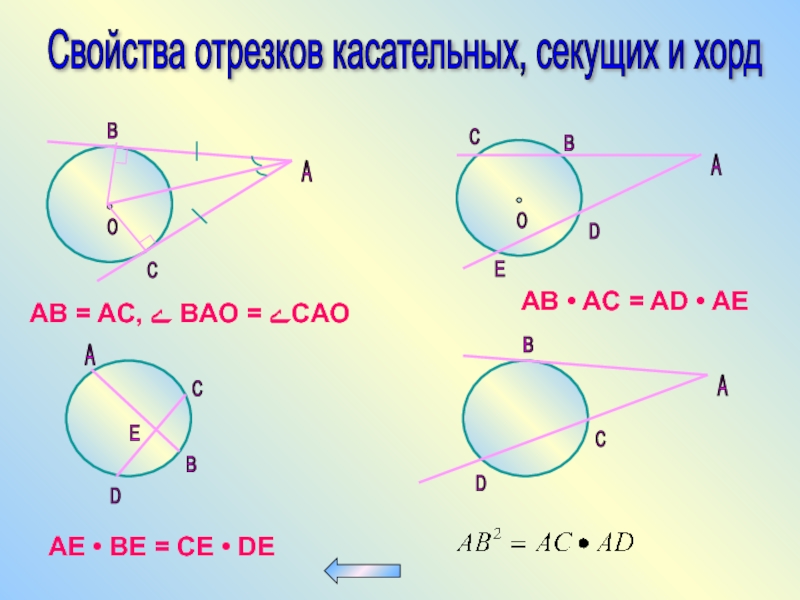
Слайд 58Свойства отрезков касательных, секущих и хорд
A
B
С
О
A
B
С
О
A
B
С
A
B
С
D
E
D
E
D
AB = AC, ے BAO = ےCAO
AB • AC = AD • AE
AE • BE = CE • DE
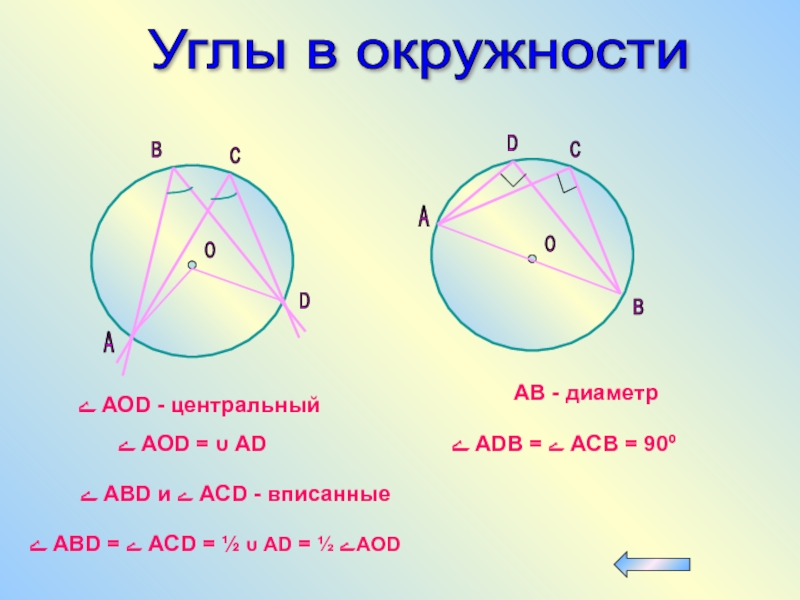
Слайд 59Углы в окружности
A
B
С
О
D
A
B
С
О
D
ے AOD - центральный
ے AOD = υ AD
ے ABD и ے ACD - вписанные
ے ABD = ے ACD = ½ υ AD = ½ ےAOD
ے ADB = ے ACB = 90º
AВ - диаметр
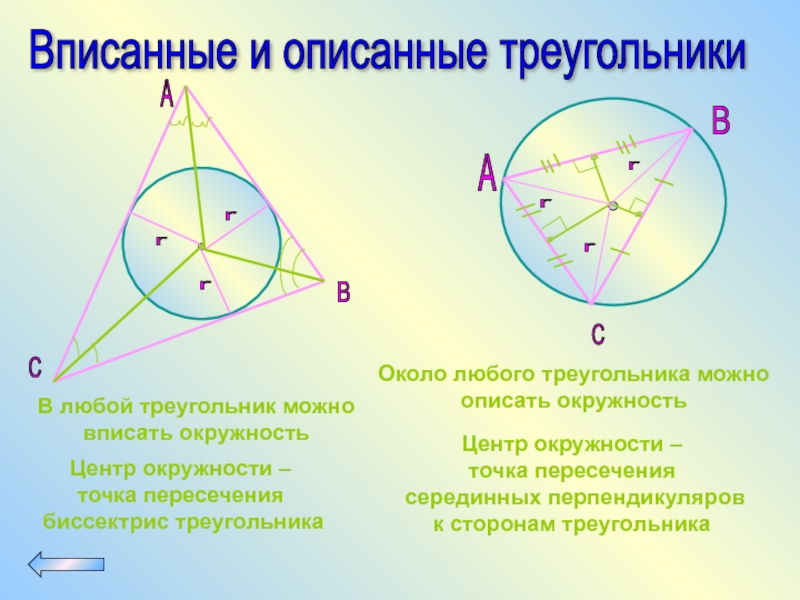
Слайд 61Вписанные и описанные треугольники
A
B
r
A
B
r
r
С
В любой треугольник можно
вписать окружность
Центр окружности –
точка пересечения
биссектрис треугольника
Около любого треугольника можно
описать окружность
Центр окружности –
точка пересечения
серединных перпендикуляров
к сторонам треугольника
С
r
r
r
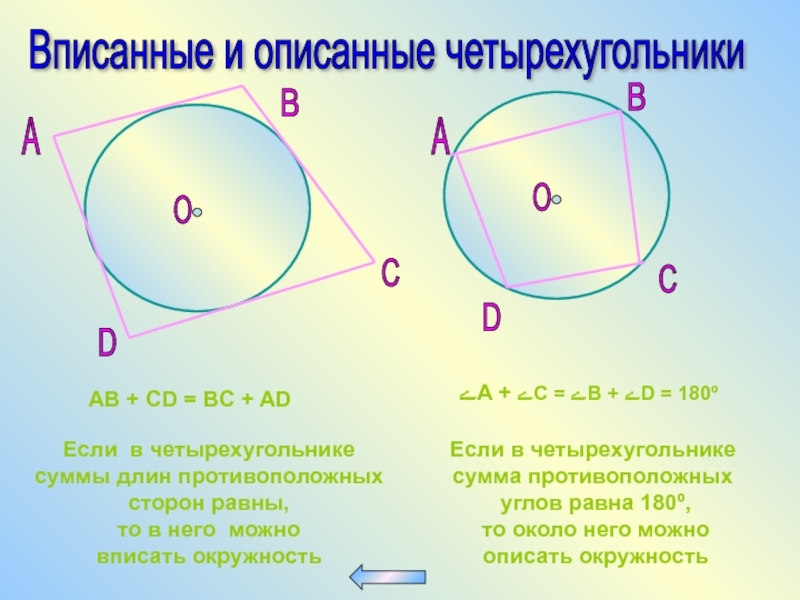
Слайд 62Вписанные и описанные четырехугольники
A
B
AB + CD = BC
+ AD
Если в четырехугольнике
суммы длин противоположных
сторон равны,
то в него можно
вписать окружность
ےA + ےC = ےB + ےD = 180º
Если в четырехугольнике
сумма противоположных
углов равна 180º,
то около него можно
описать окружность
C
D
O
A
B
C
D
O
Слайд 63Векторы на плоскости
Вектор и его координаты
Вычитание векторов
Умножение вектора
на число
Сложение векторов
Скалярное произведение векторов
Равные векторы
Слайд 70Движения
Свойства движений
Центральная симметрия
Осевая симметрия
Параллельный перенос
Поворот
Слайд 71Свойства движений
Движение – отображение плоскости на себя,
которое сохраняет расстояния между
точками
При движении отрезок отображается на отрезок
При движении треугольник отображается на
равный ему треугольник
При движении прямая отображается на прямую,
луч – на луч,
угол – на равный ему угол
