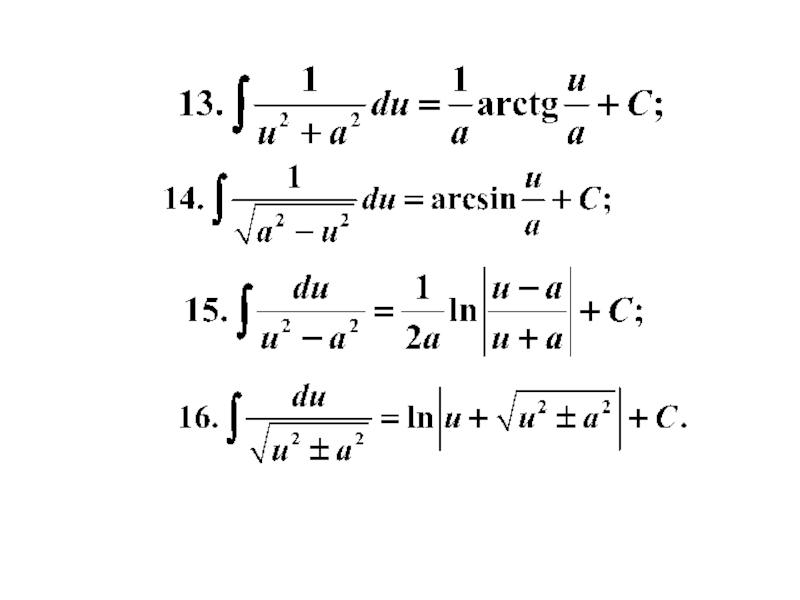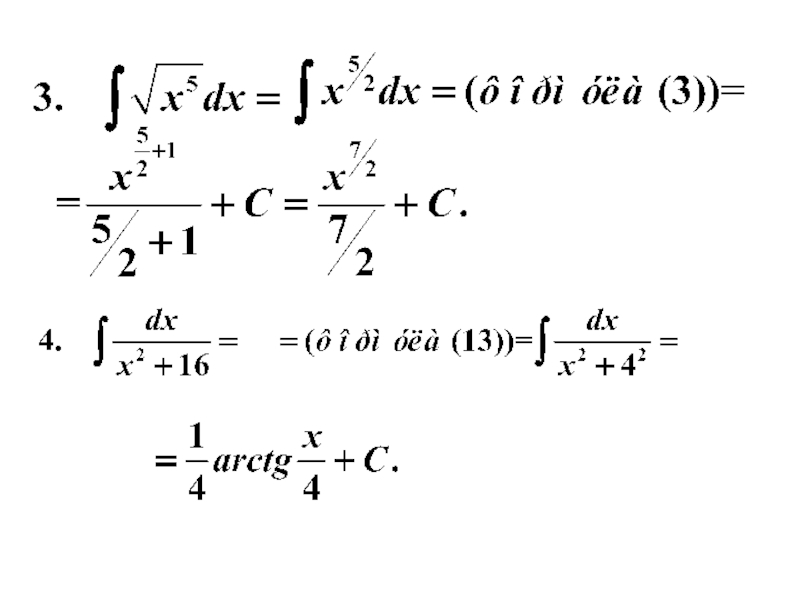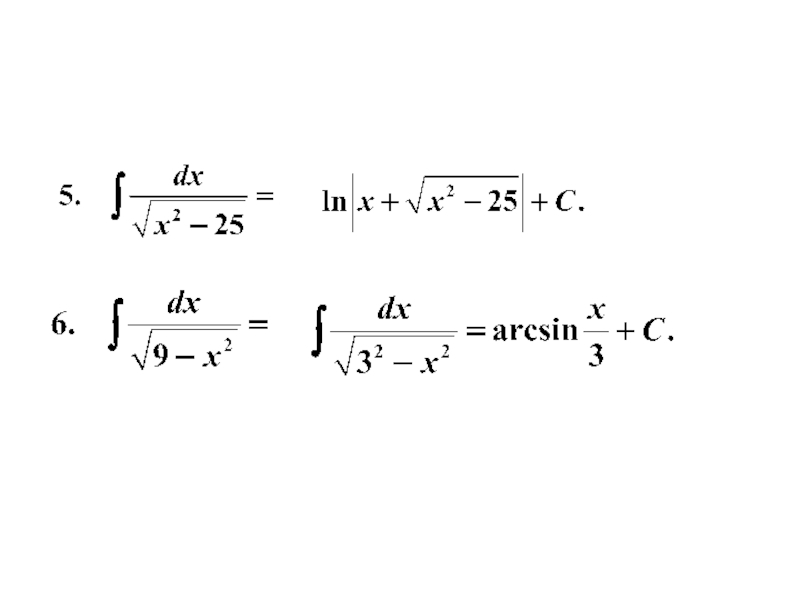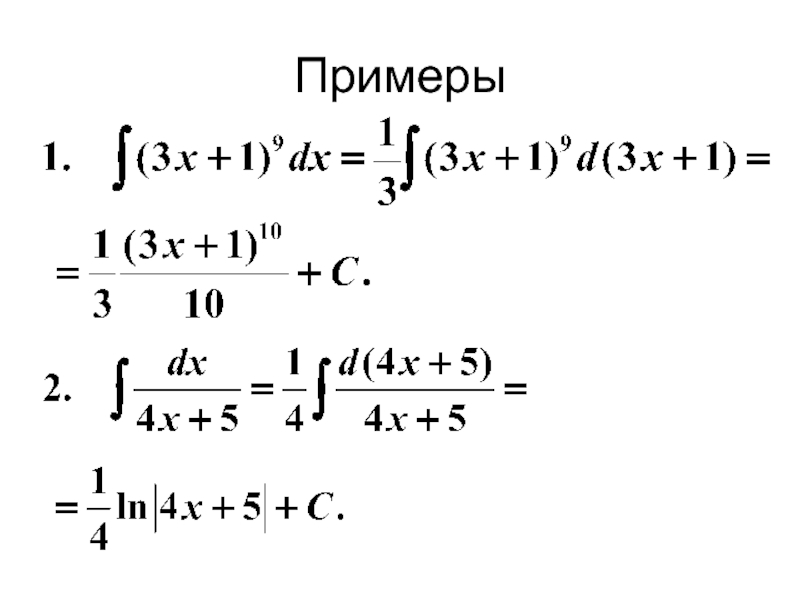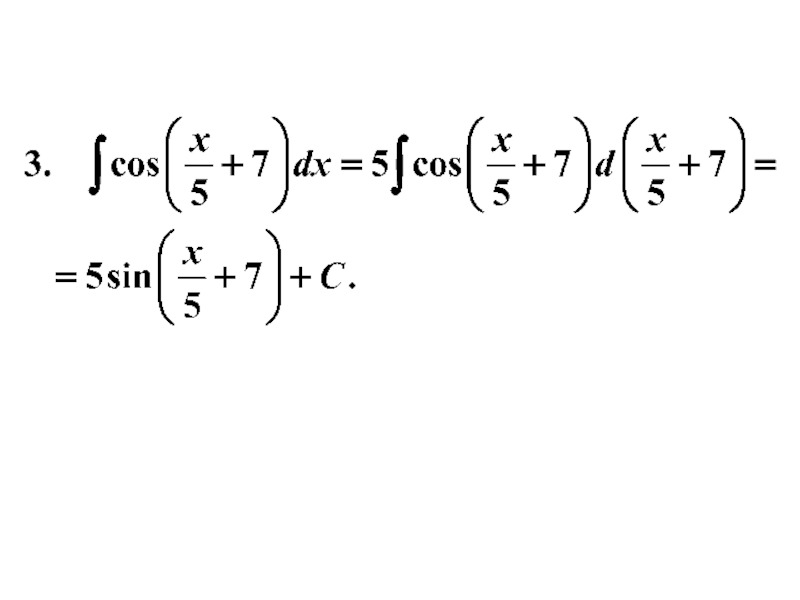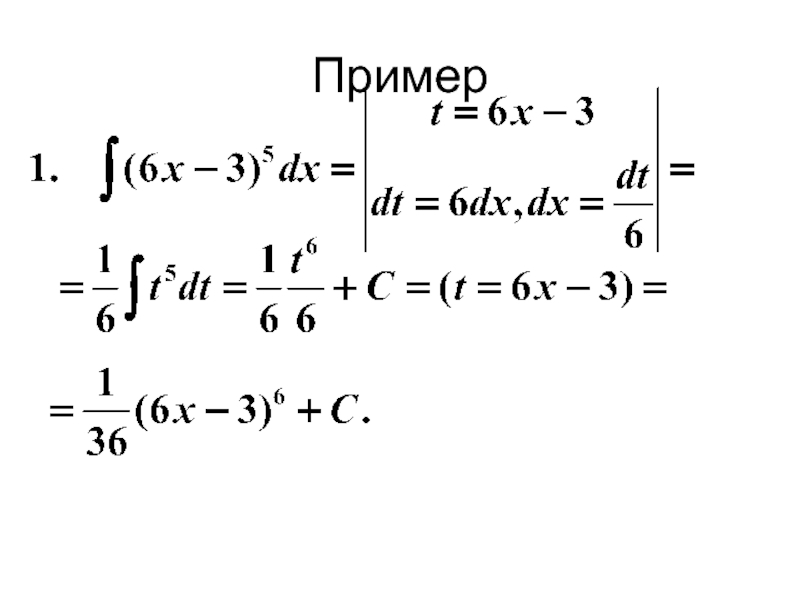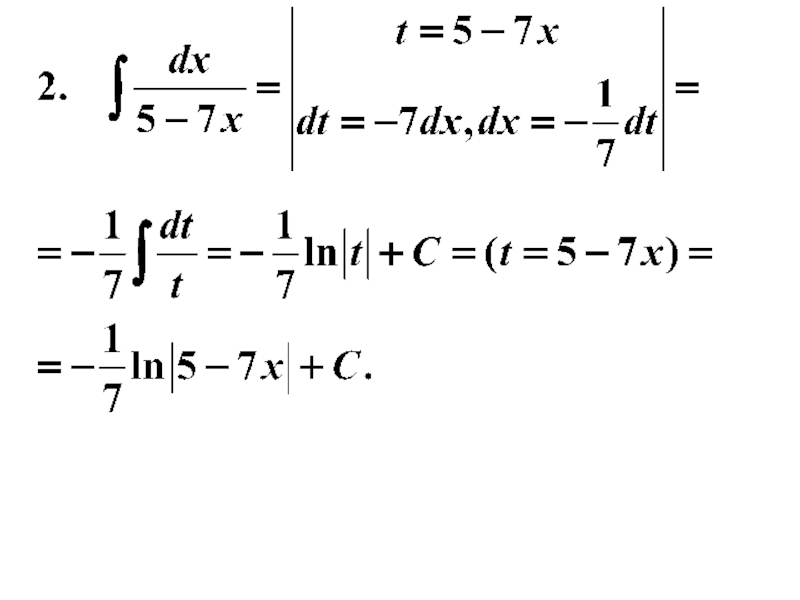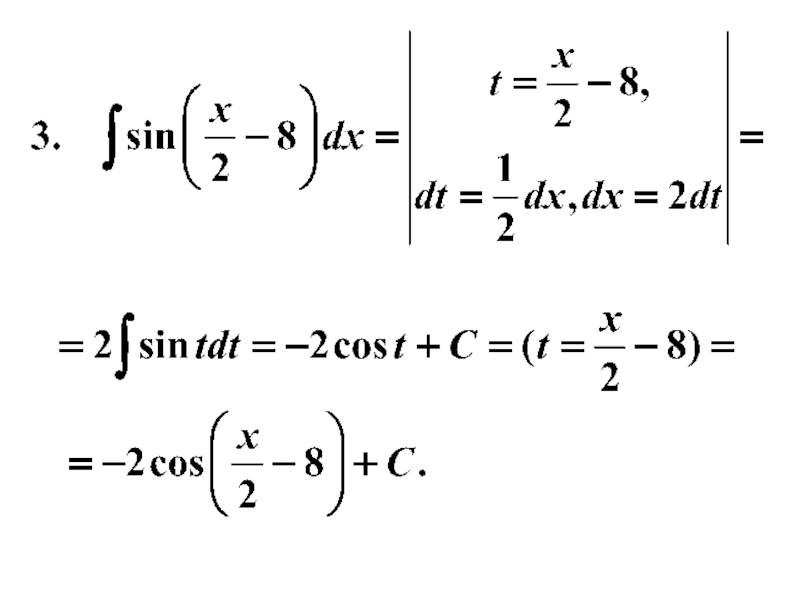- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неопределенный интеграл и его свойства презентация
Содержание
- 1. Неопределенный интеграл и его свойства
- 2. 1.1. Первообразная функция ОПР. Функция
- 3. Теорема 1.1. Если функция f(x) непрерывна на
- 4. где
- 5. Знак называется интегралом, функция
- 6. 1. Дифференциал от неопределенного интеграла равен подынтегральному выражению: Основные свойства неопределенного интеграла
- 7. 2. Производная неопределенного интеграла равна подынтегральной функции:
- 8. 3. Неопределенный интеграл от дифференциала некоторой функции
- 9. 4. Постоянный множитель можно выносить за знак интеграла:
- 10. 5. Неопределенный интеграл от алгебраической суммы конечного
- 11. 6. Если
- 12. При вычислении неопределенного интеграла используют формулу:
- 13. Таблица простейших интегралов
- 15. Вычисление интегралов с помощью преобразования подынтегрального выражения
- 16. Пример 1. Используя таблицу и свойства интегралов, найти интегралы.
- 19. Непосредственное интегрирование Метод интегрирования, при котором данный
- 20. При сведении данного интеграла к табличному часто
- 21. Примеры
- 23. Метод замены переменной (метод подстановки) состоит в
- 24. Пример
- 27. Интегрирование по частям Формула где
- 28. Некоторые типы интегралов, которые можно вычислять методом
- 29. 2. Интегралы вида Здесь полагают
- 30. Пример. Вычислить неопределенные интегралы методом интегрирования по частям.
1.1. Первообразная функция
ОПР. Функция называется первообразной для функции на
Слайд 21.1. Первообразная функция
ОПР. Функция
называется первообразной для функции на данном промежутке (a;b), если для любого x из этого промежутка
или
или
Пример. Первообразной для функции
на всей числовой оси является
так как
Слайд 3 Теорема 1.1. Если функция f(x) непрерывна на данном интервале, то на
этом интервале она имеет первообразную.
Теорема 1.2. Если функция F(x) является первообразной функции f(x) на (a;b), то множество всех первообразных для f(x) задается формулой F(x)+C, где C − постоянная.
Теорема 1.2. Если функция F(x) является первообразной функции f(x) на (a;b), то множество всех первообразных для f(x) задается формулой F(x)+C, где C − постоянная.
Слайд 4где – произвольная постоянная.
ОПР. Совокупность всех первообразных
для данной функции
называется ее неопределенным интегралом и обозначается
1.2. Неопределенный интеграл
Слайд 5Знак
называется интегралом, функция
– подынтегральной функцией,
–
подынтегральным выражением,
Операция нахождения неопределенного интеграла для данной функции называется интегрированием этой функции.
Интегрирование – операция, обратная операции дифференцирования.
– переменной интегрирования.
Слайд 6 1. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
Основные свойства неопределенного интеграла
Слайд 7 2. Производная неопределенного интеграла равна подынтегральной функции:
Таким образом,
правильность интегрирования проверяется
дифференцированием!
Слайд 8 3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции
и произвольной постоянной:
Слайд 10 5. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен
алгебраической сумме интегралов от слагаемых функций:
Слайд 11 6. Если
то
где − произвольная функция, имеющая непрерывную производную.
Данное свойство называется инвариантностью неопределенного интеграла.
где − произвольная функция, имеющая непрерывную производную.
Данное свойство называется инвариантностью неопределенного интеграла.
Слайд 15 Вычисление интегралов с помощью преобразования подынтегрального выражения к табличной форме и
использования свойств неопределенного интеграла называется непосредственным интегрированием.
Вспомогательные сведения
Слайд 19Непосредственное интегрирование
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной
функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредствен-ным интегрированием.
1.3. Основные методы вычисления неопределенных интегралов
Слайд 20 При сведении данного интеграла к табличному часто используется следующее преобразование дифференциала
(операция «подведения под знак дифференциала»).
Например:
Например:
Слайд 23 Метод замены переменной (метод подстановки) состоит в преобразовании интеграла
в другой интеграл
который вычисляется проще, чем исходный.
который вычисляется проще, чем исходный.
Интегрирование заменой переменной
Слайд 27Интегрирование по частям
Формула
где
и – дифференцируемые функции, называется
формулой интегрирования по частям.
Метод интегрирования по частям целесообразно применять, если
более прост в вычислении, чем
формулой интегрирования по частям.
Метод интегрирования по частям целесообразно применять, если
более прост в вычислении, чем
Слайд 28Некоторые типы интегралов, которые можно вычислять методом интегрирования по частям
Интегралы вида
где
− многочлен, m − число.
Здесь полагают
за обозначают остальные сомножители.
Здесь полагают
за обозначают остальные сомножители.
Слайд 292. Интегралы вида
Здесь полагают
за u обозначают остальные сомножители.
3.
Интегралы вида
где a и b − числа.
За u можно принять функцию
где a и b − числа.
За u можно принять функцию
