- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аксонометрические проекции геометрических тел презентация
Содержание
- 1. Аксонометрические проекции геометрических тел
- 2. Геометрические тела Геометрическим телом называется
- 3. Многогранники Геометрические тела, поверхность которых ограничена
- 4. Призма Призмой называется многогранник, основаниями которого
- 5. Типы призм Если основаниями призмы являются
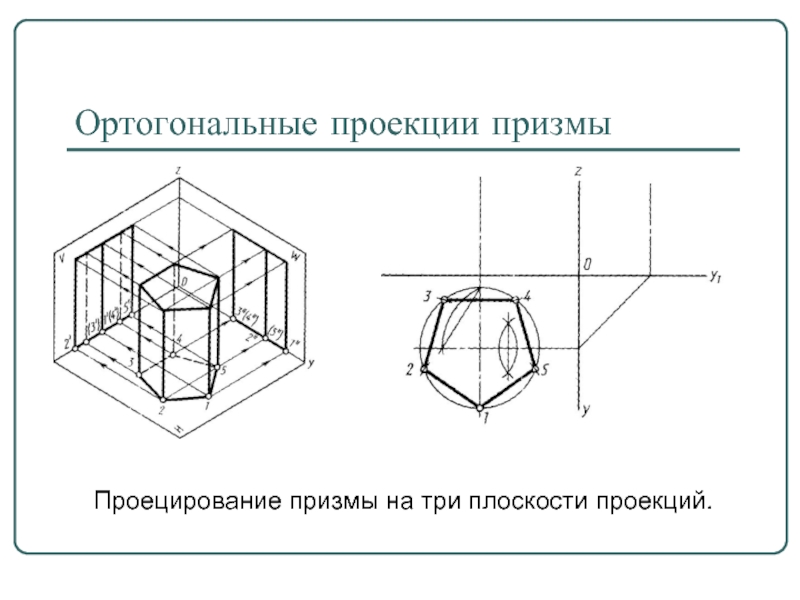
- 6. Ортогональные проекции призмы Проецирование призмы на три плоскости проекций.
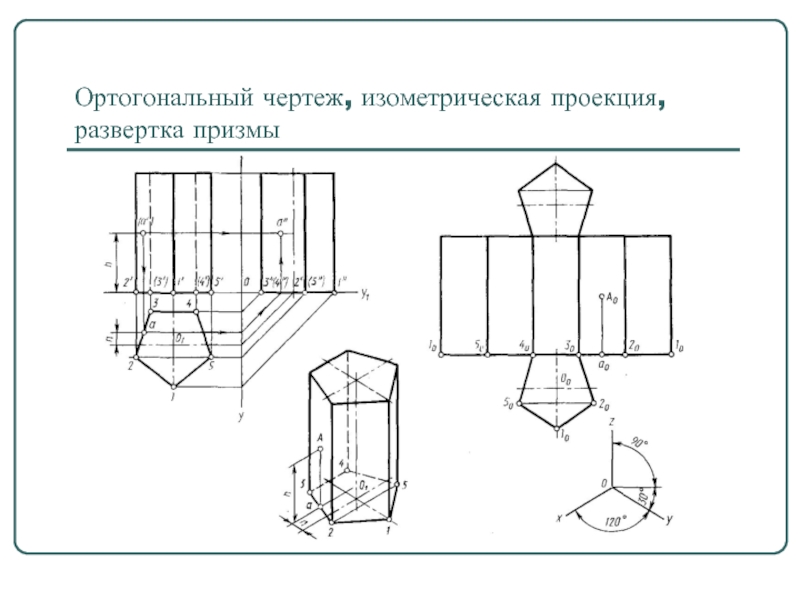
- 7. Ортогональный чертеж, изометрическая проекция, развертка призмы
- 8. Пирамида
- 9. Типы пирамид
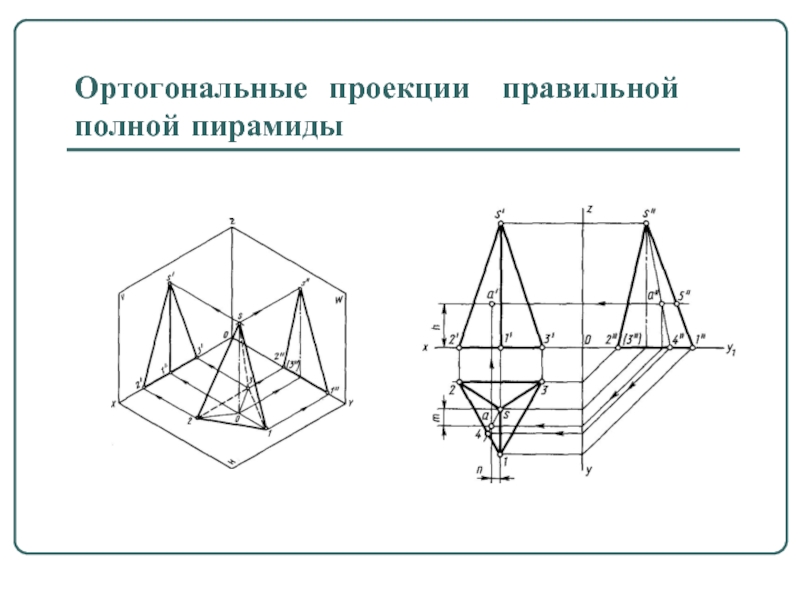
- 10. Ортогональные проекции правильной полной пирамиды
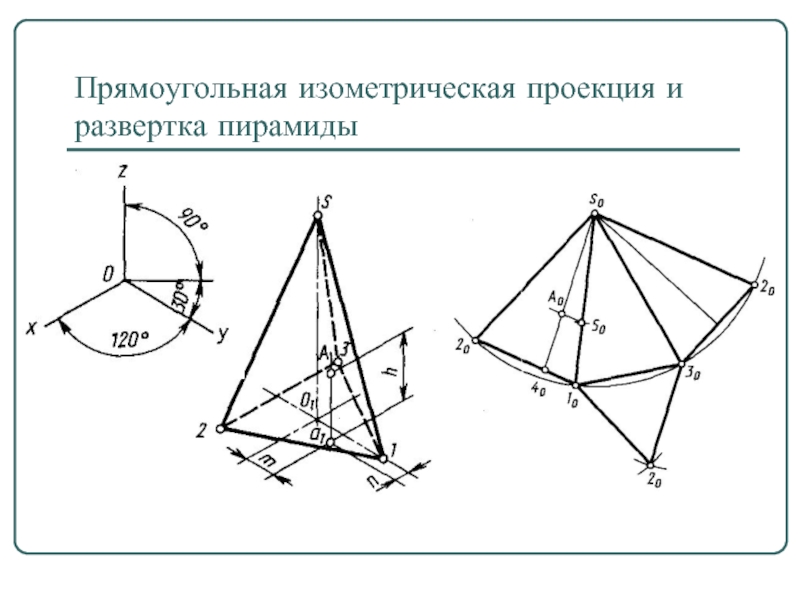
- 11. Прямоугольная изометрическая проекция и развертка пирамиды
- 12. ТЕЛА ВРАЩЕНИЯ Кривые поверхности образуются
- 13. Поверхности вращения
- 14. Цилиндр Цилиндр — геометрическое тело, ограниченное
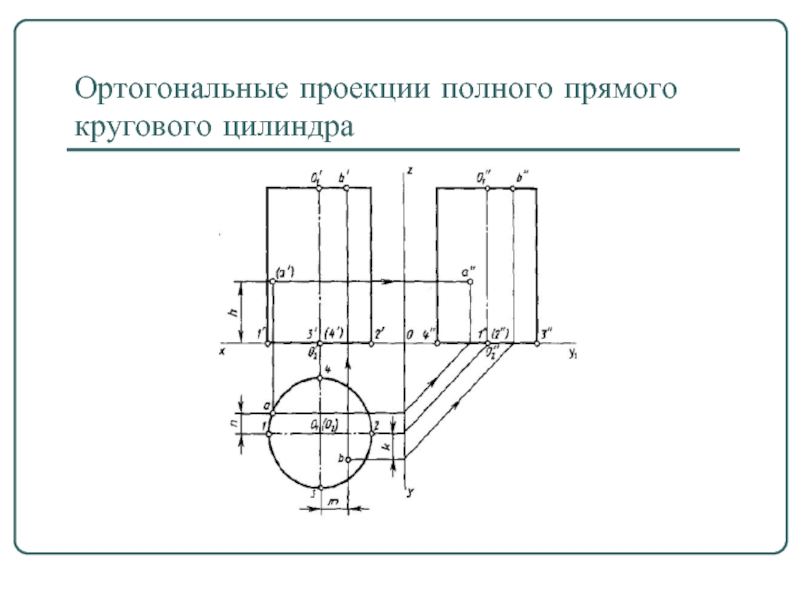
- 15. Ортогональные проекции полного прямого кругового цилиндра
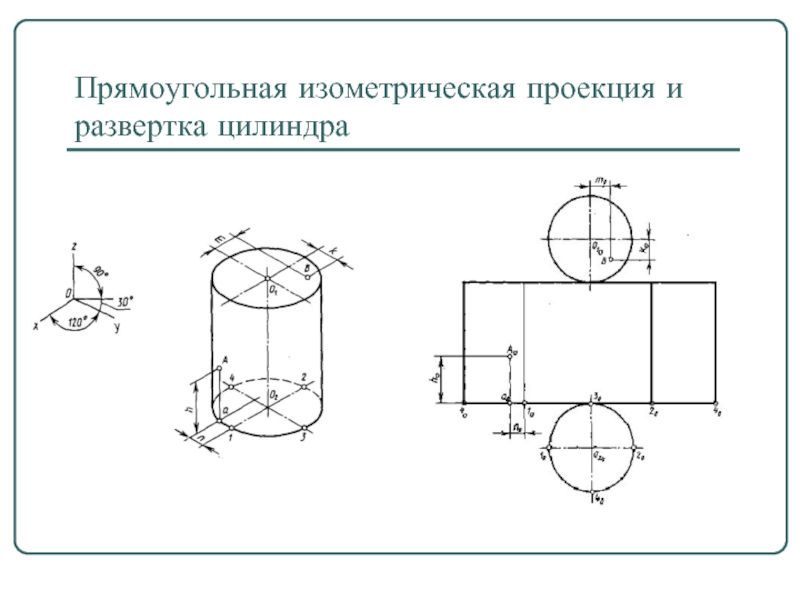
- 16. Прямоугольная изометрическая проекция и развертка цилиндра
- 17. Конус Конус —геометрическое тело, ограниченное конической поверхностью
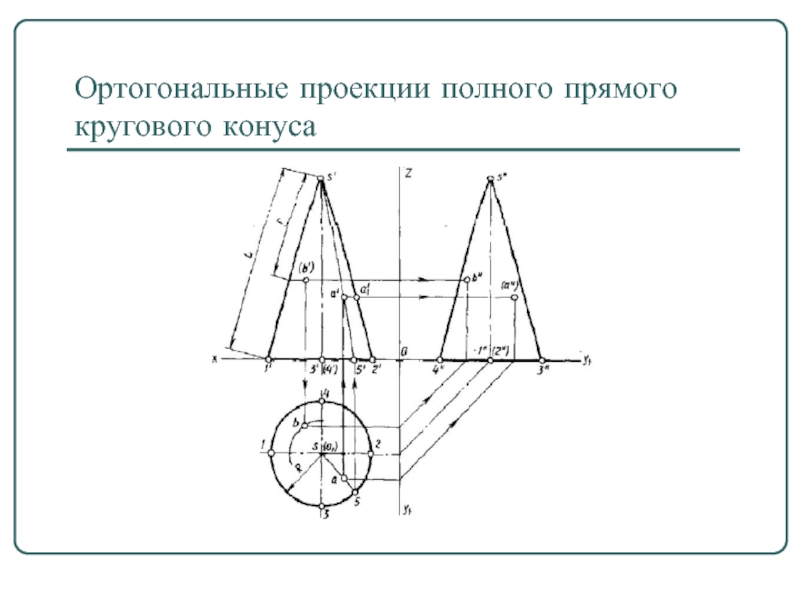
- 18. Ортогональные проекции полного прямого кругового конуса
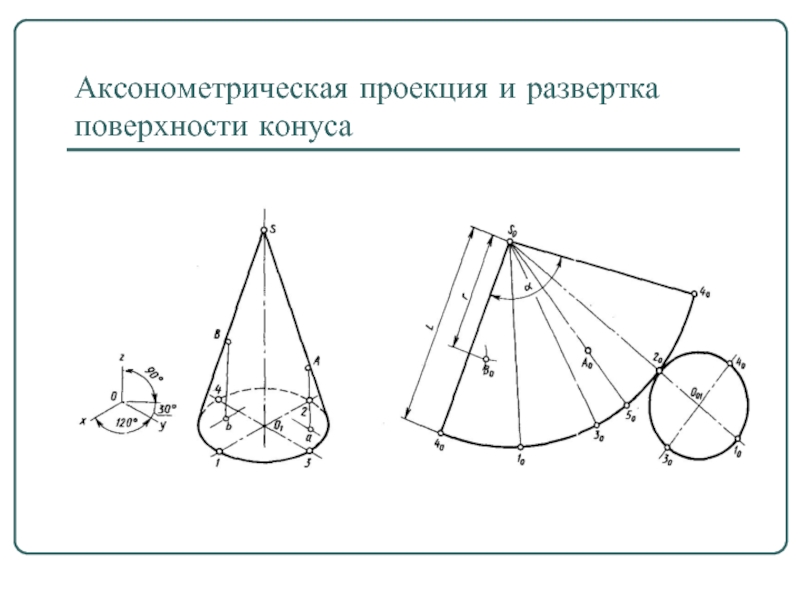
- 19. Аксонометрическая проекция и развертка поверхности конуса
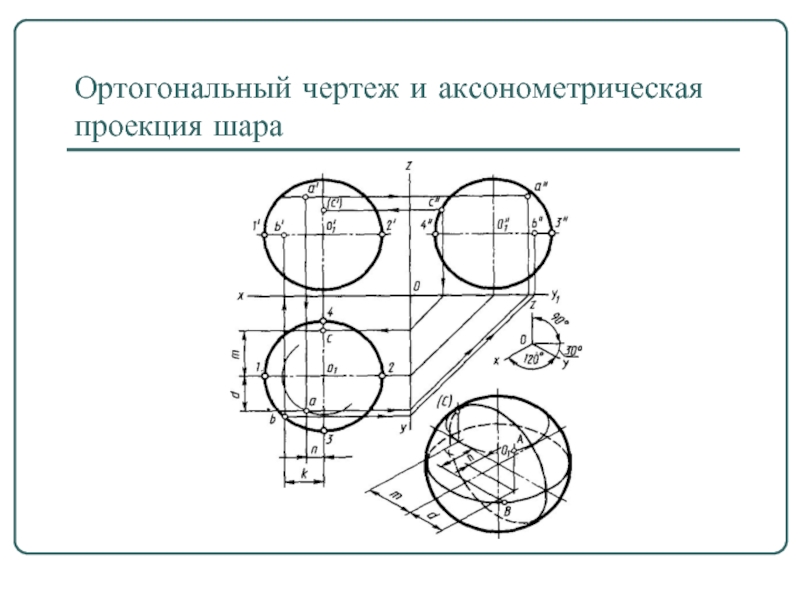
- 20. Ортогональный чертеж и аксонометрическая проекция шара
- 21. СПАСИБО ЗА ВНИМАНИЕ
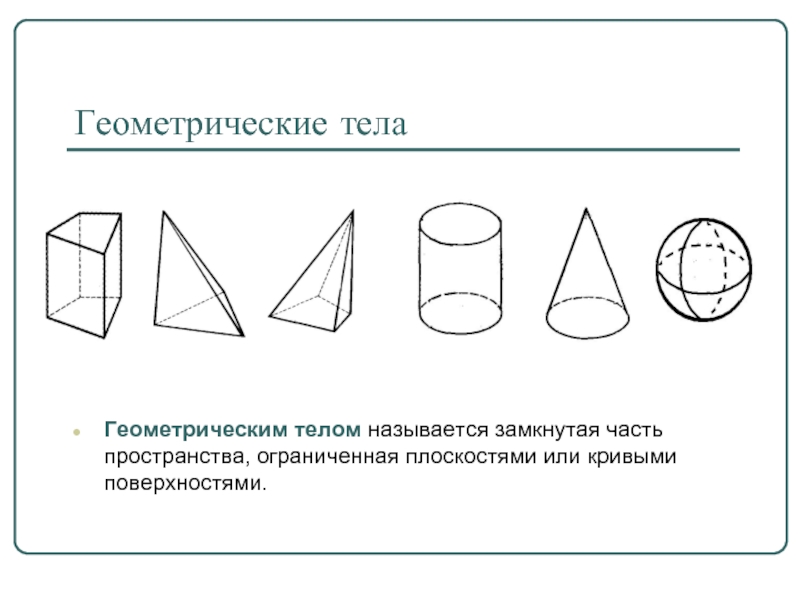
Слайд 2Геометрические тела
Геометрическим телом называется замкнутая часть пространства, ограниченная плоскостями или кривыми
поверхностями.
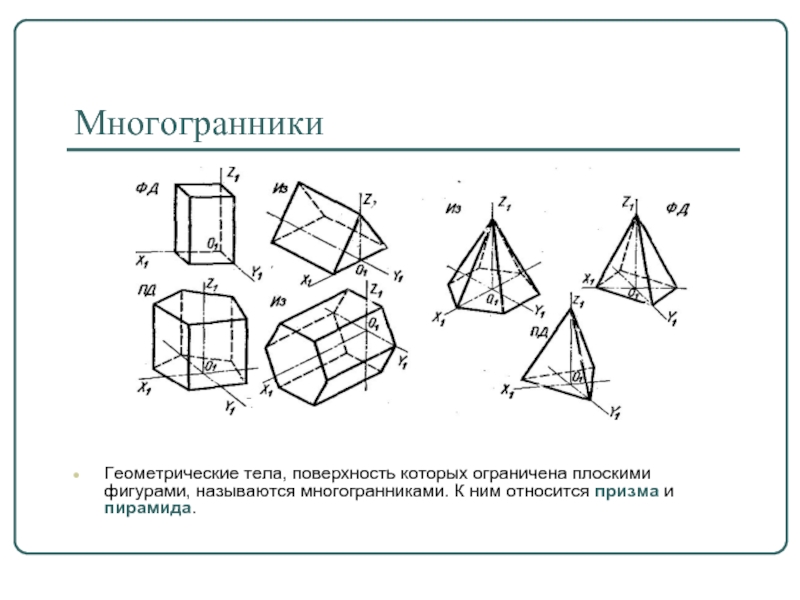
Слайд 3Многогранники
Геометрические тела, поверхность которых ограничена плоскими фигурами, называются многогранниками. К ним
относится призма и пирамида.
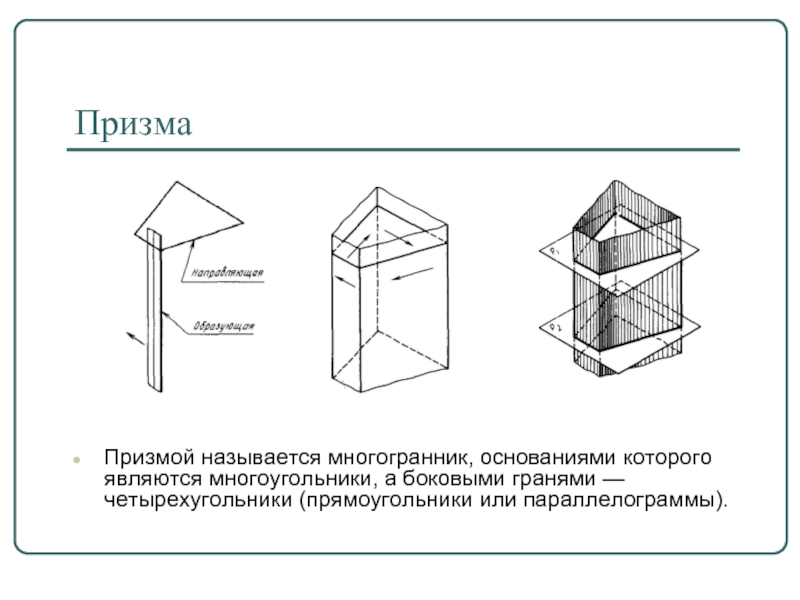
Слайд 4Призма
Призмой называется многогранник, основаниями которого являются многоугольники, а боковыми гранями —
четырехугольники (прямоугольники или параллелограммы).
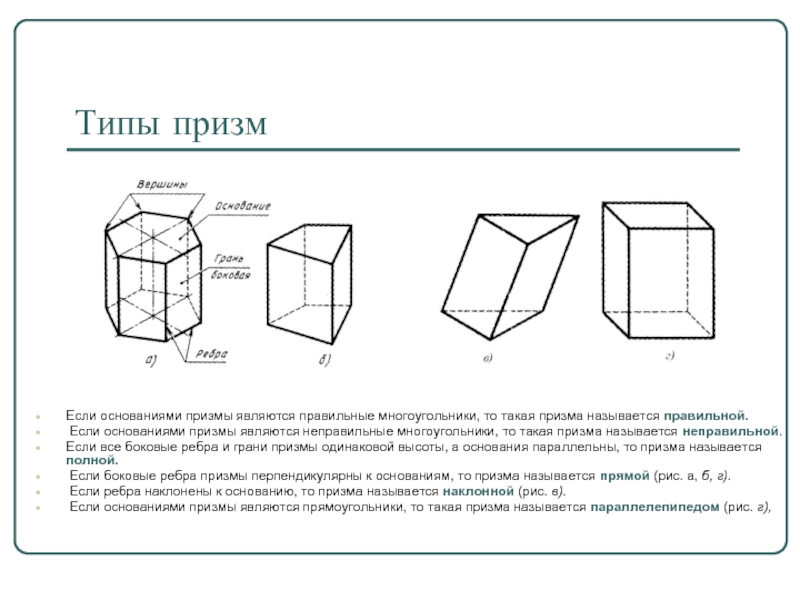
Слайд 5Типы призм
Если основаниями призмы являются правильные многоугольники, то такая призма называется
правильной.
Если основаниями призмы являются неправильные многоугольники, то такая призма называется неправильной.
Если все боковые ребра и грани призмы одинаковой высоты, а основания параллельны, то призма называется полной.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой (рис. а, б, г).
Если ребра наклонены к основанию, то призма называется наклонной (рис. в).
Если основаниями призмы являются прямоугольники, то такая призма называется параллелепипедом (рис. г),
Если основаниями призмы являются неправильные многоугольники, то такая призма называется неправильной.
Если все боковые ребра и грани призмы одинаковой высоты, а основания параллельны, то призма называется полной.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой (рис. а, б, г).
Если ребра наклонены к основанию, то призма называется наклонной (рис. в).
Если основаниями призмы являются прямоугольники, то такая призма называется параллелепипедом (рис. г),
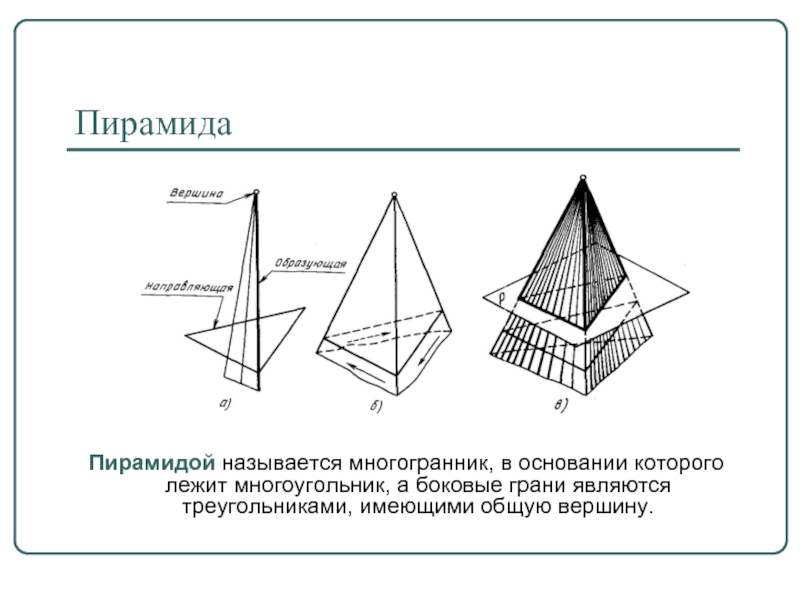
Слайд 8Пирамида
Пирамидой называется многогранник, в основании которого
лежит многоугольник, а боковые грани являются треугольниками, имеющими общую вершину.
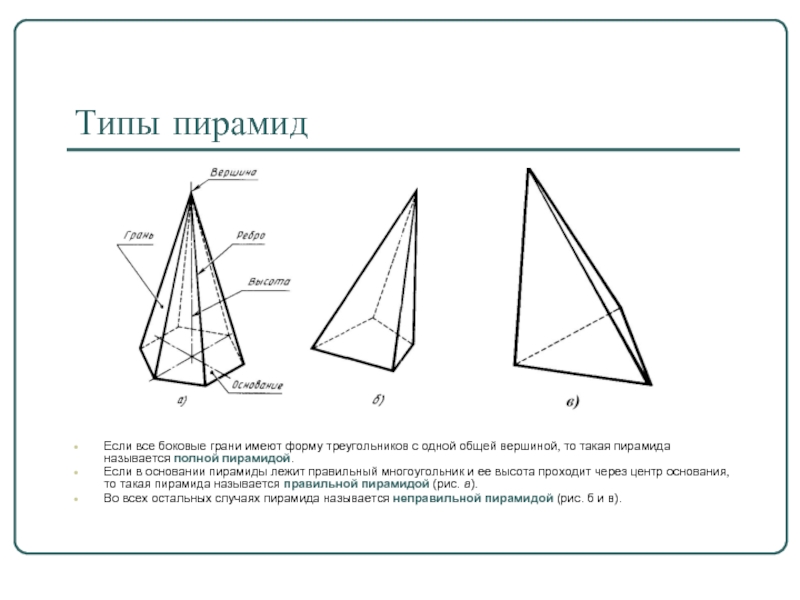
Слайд 9Типы пирамид
Если все боковые грани имеют форму треугольников с одной общей
вершиной, то такая пирамида называется полной пирамидой.
Если в основании пирамиды лежит правильный многоугольник и ее высота проходит через центр основания, то такая пирамида называется правильной пирамидой (рис. а).
Во всех остальных случаях пирамида называется неправильной пирамидой (рис. б и в).
Если в основании пирамиды лежит правильный многоугольник и ее высота проходит через центр основания, то такая пирамида называется правильной пирамидой (рис. а).
Во всех остальных случаях пирамида называется неправильной пирамидой (рис. б и в).
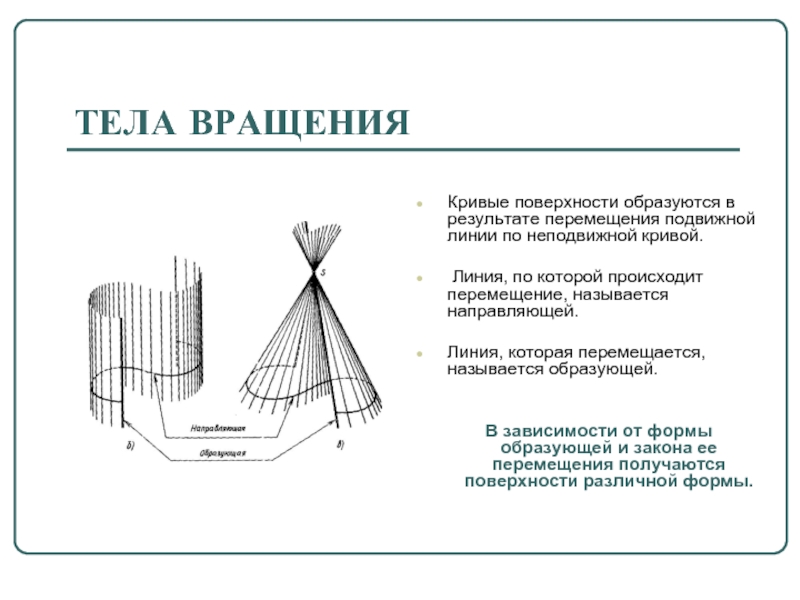
Слайд 12ТЕЛА ВРАЩЕНИЯ
Кривые поверхности образуются в результате перемещения подвижной линии по
неподвижной кривой.
Линия, по которой происходит перемещение, называется направляющей.
Линия, которая перемещается, называется образующей.
В зависимости от формы образующей и закона ее перемещения получаются поверхности различной формы.
Линия, по которой происходит перемещение, называется направляющей.
Линия, которая перемещается, называется образующей.
В зависимости от формы образующей и закона ее перемещения получаются поверхности различной формы.
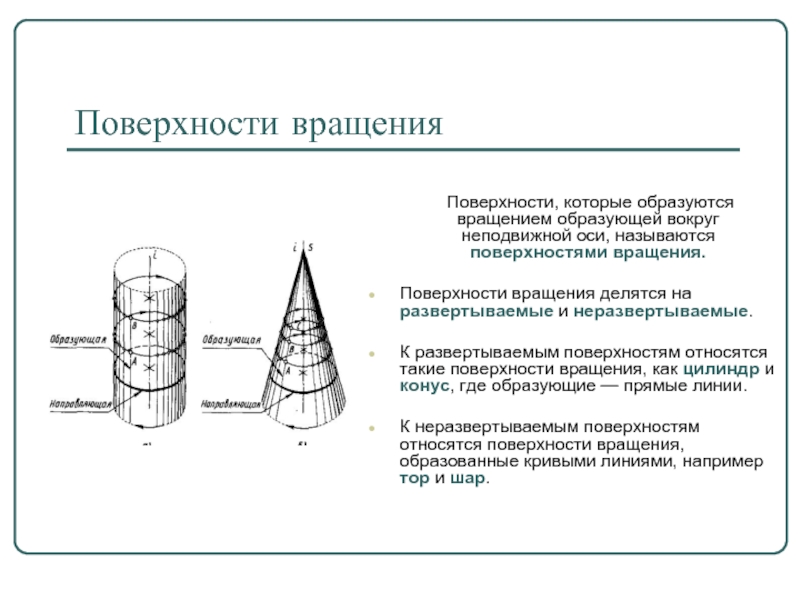
Слайд 13Поверхности вращения
Поверхности, которые образуются вращением образующей вокруг
неподвижной оси, называются поверхностями вращения.
Поверхности вращения делятся на развертываемые и неразвертываемые.
К развертываемым поверхностям относятся такие поверхности вращения, как цилиндр и конус, где образующие — прямые линии.
К неразвертываемым поверхностям относятся поверхности вращения, образованные кривыми линиями, например тор и шар.
Поверхности вращения делятся на развертываемые и неразвертываемые.
К развертываемым поверхностям относятся такие поверхности вращения, как цилиндр и конус, где образующие — прямые линии.
К неразвертываемым поверхностям относятся поверхности вращения, образованные кривыми линиями, например тор и шар.
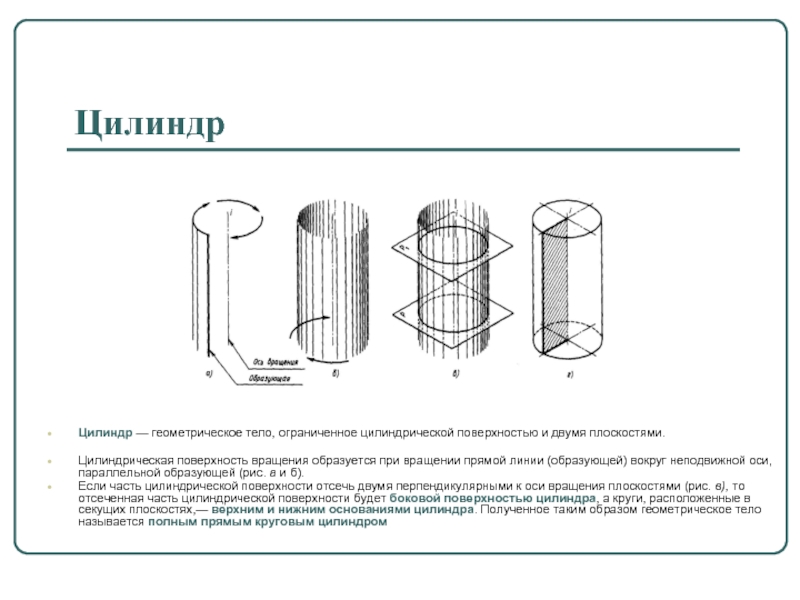
Слайд 14Цилиндр
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями.
Цилиндрическая поверхность
вращения образуется при вращении прямой линии (образующей) вокруг неподвижной оси, параллельной образующей (рис. а и б).
Если часть цилиндрической поверхности отсечь двумя перпендикулярными к оси вращения плоскостями (рис. в), то отсеченная часть цилиндрической поверхности будет боковой поверхностью цилиндра, а круги, расположенные в секущих плоскостях,— верхним и нижним основаниями цилиндра. Полученное таким образом геометрическое тело называется полным прямым круговым цилиндром
Если часть цилиндрической поверхности отсечь двумя перпендикулярными к оси вращения плоскостями (рис. в), то отсеченная часть цилиндрической поверхности будет боковой поверхностью цилиндра, а круги, расположенные в секущих плоскостях,— верхним и нижним основаниями цилиндра. Полученное таким образом геометрическое тело называется полным прямым круговым цилиндром
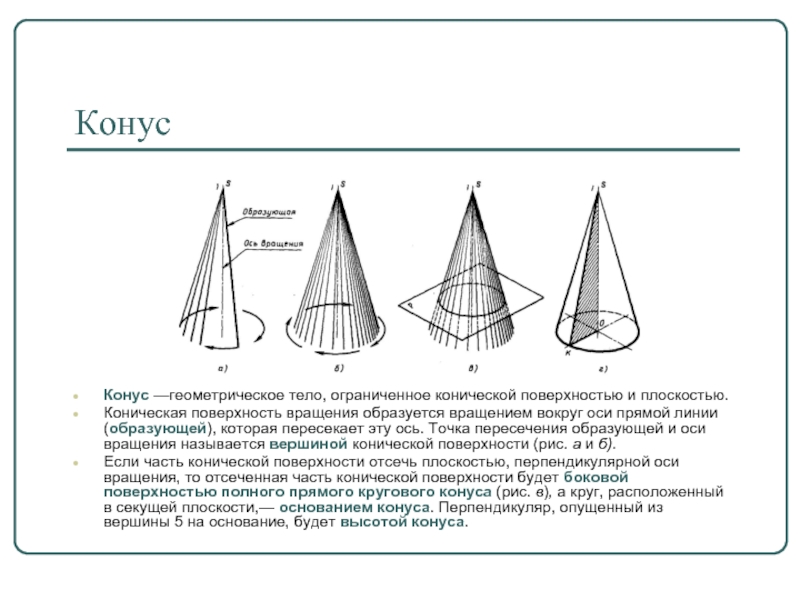
Слайд 17Конус
Конус —геометрическое тело, ограниченное конической поверхностью и плоскостью.
Коническая поверхность вращения образуется
вращением вокруг оси прямой линии (образующей), которая пересекает эту ось. Точка пересечения образующей и оси вращения называется вершиной конической поверхности (рис. а и б).
Если часть конической поверхности отсечь плоскостью, перпендикулярной оси вращения, то отсеченная часть конической поверхности будет боковой поверхностью полного прямого кругового конуса (рис. в), а круг, расположенный в секущей плоскости,— основанием конуса. Перпендикуляр, опущенный из вершины 5 на основание, будет высотой конуса.
Если часть конической поверхности отсечь плоскостью, перпендикулярной оси вращения, то отсеченная часть конической поверхности будет боковой поверхностью полного прямого кругового конуса (рис. в), а круг, расположенный в секущей плоскости,— основанием конуса. Перпендикуляр, опущенный из вершины 5 на основание, будет высотой конуса.