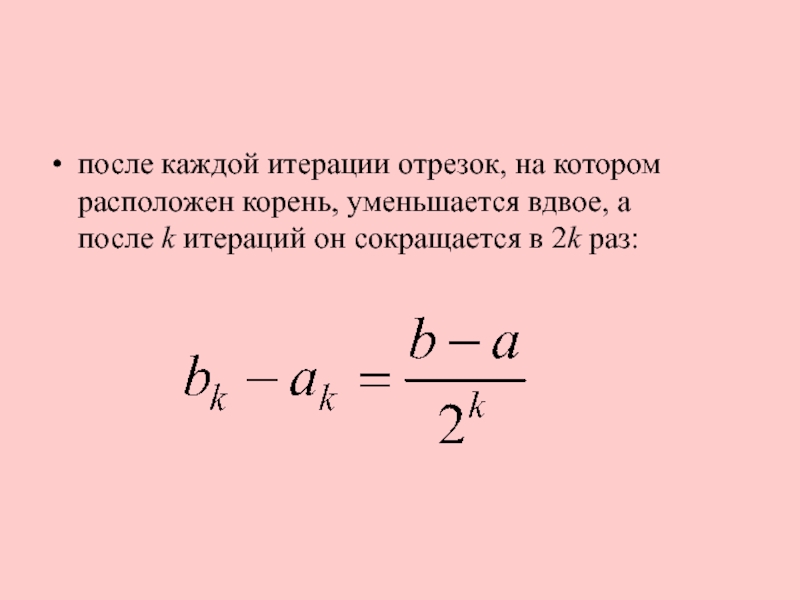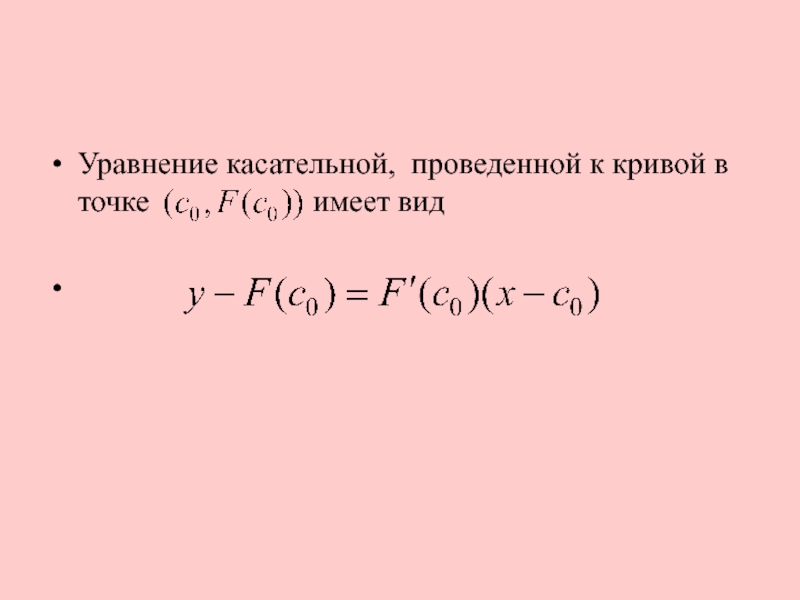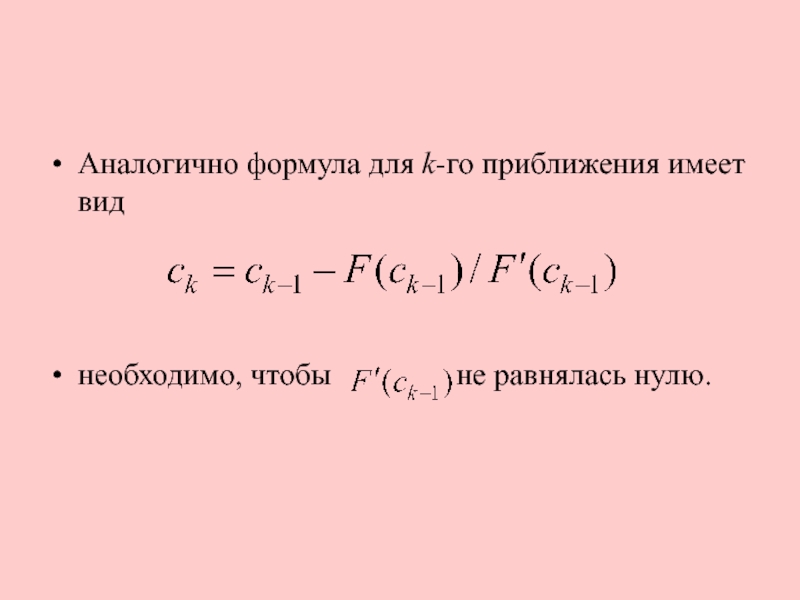- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нелинейные уравнения презентация
Содержание
- 1. Нелинейные уравнения
- 2. Нелинейные уравнения: алгебраические (содержащие только алгебраические
- 3. 1. Метод деления отрезка пополам (метод бисекции).
- 4. Далее исследуем значения функции
- 5. В качестве первого приближения корня принимаем
- 6. Таким образом, k-е приближение вычисляется как
- 7. после каждой итерации отрезок, на котором
- 8. Пусть приближенное решение требуется
- 9. Последнее неравенство выполнено, если
- 11. метод деления отрезка пополам всегда сходится,
- 12. 2. Метод хорд. Процесс
- 13. Сначала находим уравнение хорды ab:
- 14. Для точки пересечения ее с осью абсцисс получим уравнение
- 15. Далее, сравнивая знаки величин
- 16. В качестве условия окончания итераций используется условие близости двух последовательных приближений
- 18. 3. Метод Ньютона (метод касательных).
- 19. При этом не обязательно задавать отрезок
- 20. Уравнение касательной, проведенной к кривой в
- 21. Отсюда найдем следующее приближение корня как
- 22. Аналогично формула для k-го приближения имеет
- 24. для погрешности корня
- 25. 4. Метод простой итерации.
- 26. Пусть известно начальное приближение корня
- 27. Подставляя каждый раз новое значение корня в уравнение получаем последовательность значений
- 28. Итерационный процесс прекращается, если результаты двух
Нелинейные уравнения: алгебраические (содержащие только алгебраические функции (целые, рациональные, иррациональные) трансцендентные (содержащие другие функции (тригонометрические, показа- показательные, логарифмические и др.)).
Слайд 2Нелинейные уравнения:
алгебраические (содержащие только алгебраические функции (целые, рациональные, иррациональные)
трансцендентные (содержащие другие
функции (тригонометрические, показа- показательные, логарифмические и др.)).
Слайд 31. Метод деления отрезка пополам (метод бисекции).
Пусть мы нашли отрезок
, на котором функция меняет знак , т.е. на котором находится значение корня , т. е.
В качестве начального приближения корня принимаем середину этого отрезка:
В качестве начального приближения корня принимаем середину этого отрезка:
Слайд 4Далее исследуем значения функции на
концах отрезков и
Тот из отрезков, на концах которого принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка .
Тот из отрезков, на концах которого принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка .
Слайд 7
после каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а
после k итераций он сокращается в 2k раз:
Слайд 8Пусть приближенное решение требуется найти с точностью до
некоторого заданного малого числа :
Взяв в качестве приближенного решения k-е приближение корня: , учитывая, что
получим
Взяв в качестве приближенного решения k-е приближение корня: , учитывая, что
получим
Слайд 11
метод деления отрезка пополам всегда сходится, причем можно гарантировать, что полученное
решение будет иметь любую наперед заданную точность.
Слайд 12
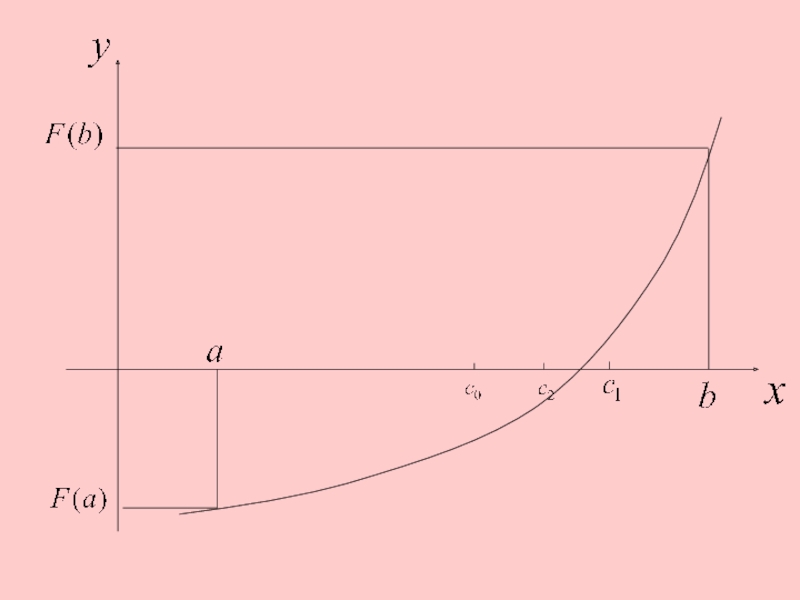
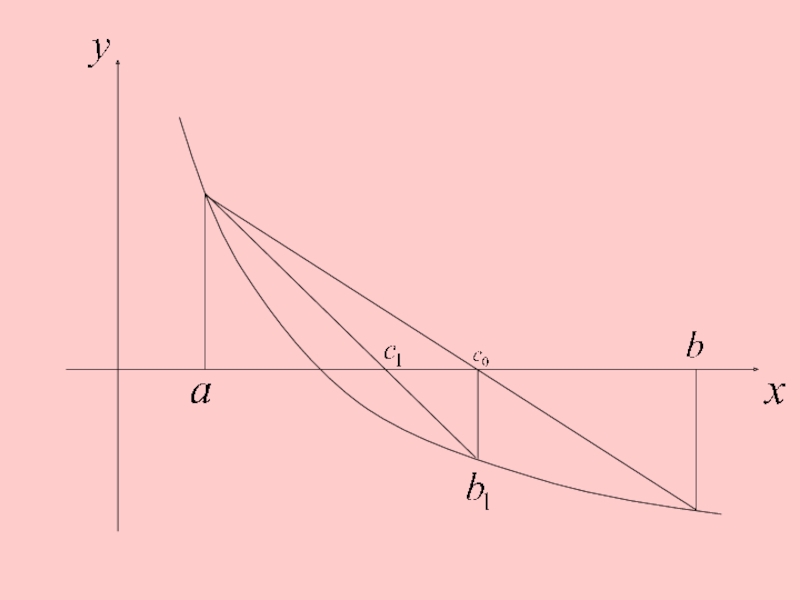
2. Метод хорд.
Процесс итераций состоит в том, что в качестве
приближений корню уравнения принимаются значения точек пересечения хорды с осью абсцисс.
( Для определенности примем )
( Для определенности примем )
Слайд 15Далее, сравнивая знаки величин и
для рассматриваемого случая, приходим к выводу, что корень находится в интервале так как
. Отрезок отбрасываем.
и т.д.
. Отрезок отбрасываем.
и т.д.
Слайд 16В качестве условия окончания итераций используется условие близости двух последовательных приближений
Слайд 18
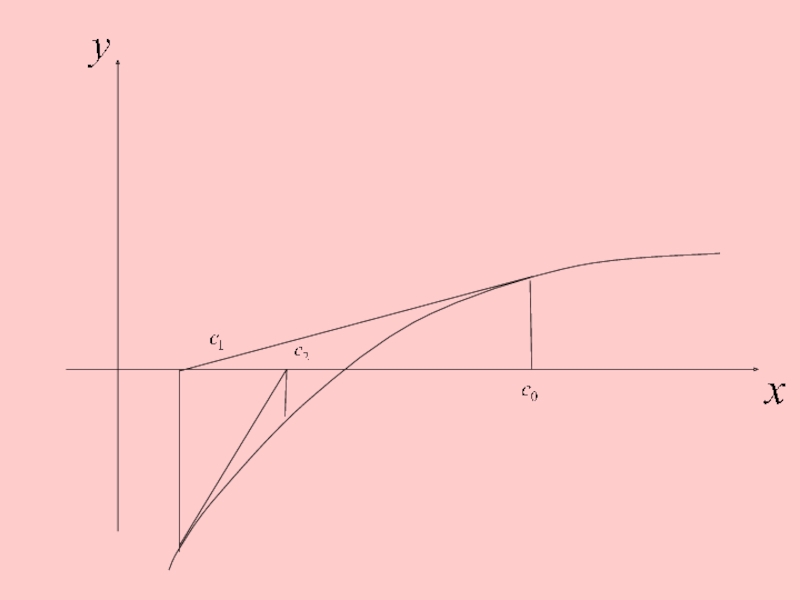
3. Метод Ньютона (метод касательных).
метод состоит в том, что на
k-й итерации проводится касательная к кривой у = F(x) и ищется точка пересечения касательной с осью абсцисс.
Слайд 19
При этом не обязательно задавать отрезок
, содержащий корень уравнения, а достаточно лишь найти некоторое начальное приближение корня
Слайд 21
Отсюда найдем следующее приближение корня как абсциссу точки пересечения касательной с
осью х (у = 0):
Слайд 25
4. Метод простой итерации.
Для использования этого метода исход- исходное нелинейное
уравнение записывается в виде
Слайд 26
Пусть известно начальное приближение корня
Подставляя это значение в правую часть
уравнения получаем новое приближение
Слайд 28
Итерационный процесс прекращается, если результаты двух последовательных итераций близки, т. е.
если выполнено неравенство
