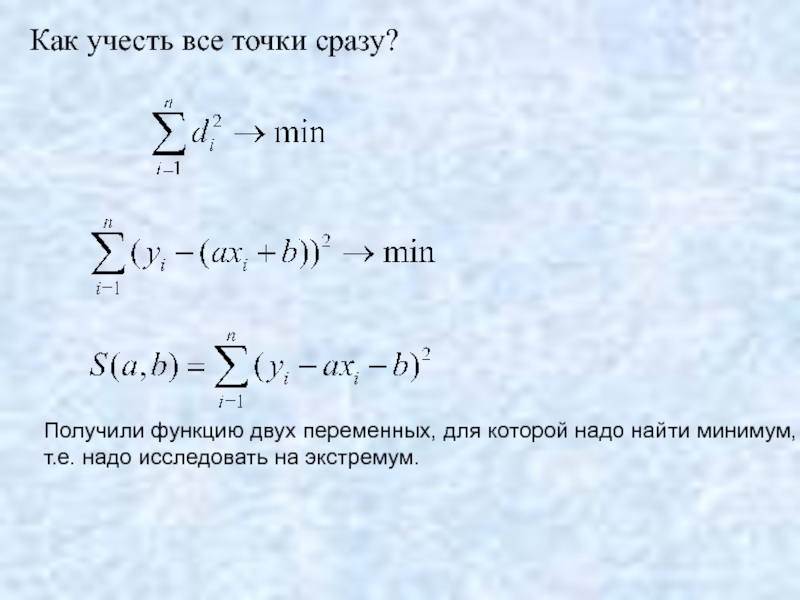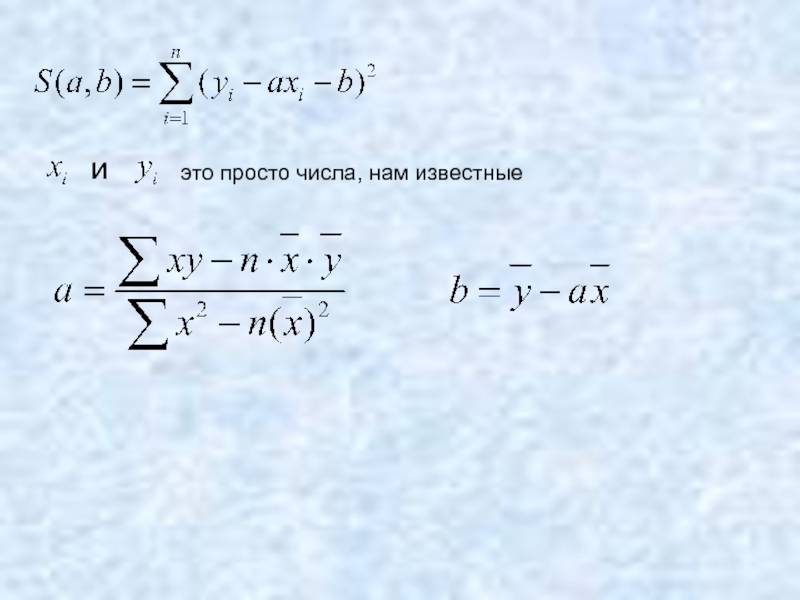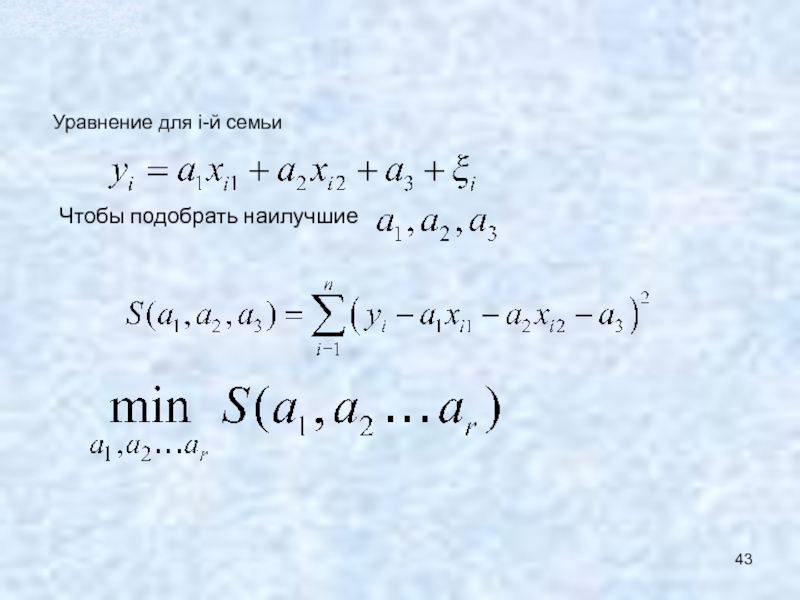переменная
a b – неизвестные параметры модели
- случайная составляющая
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модель парной линейной регрессии презентация
Содержание
- 1. Модель парной линейной регрессии
- 2. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
- 3. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
- 4. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ Нанесем точки на график
- 5. Метод наименьших квадратов Нанесем точки
- 6. Метод наименьших квадратов Нанесем точки
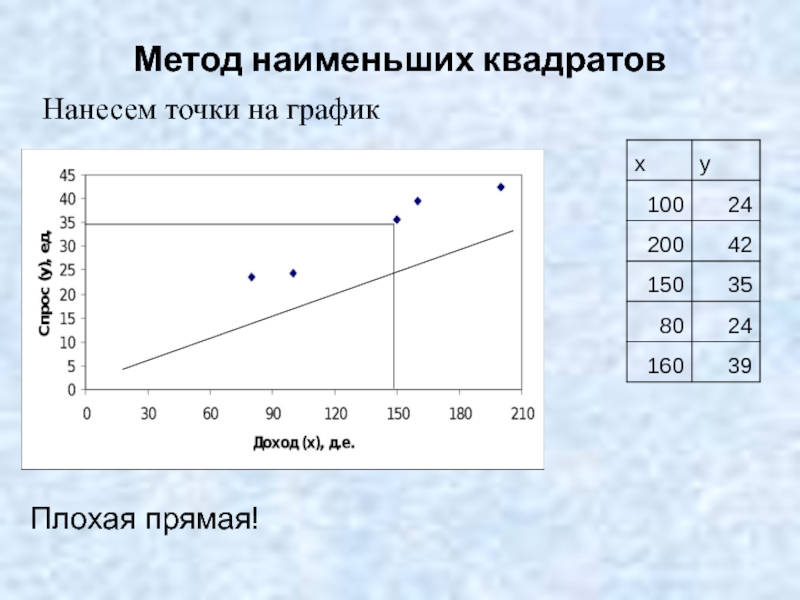
- 7. Метод наименьших квадратов Нанесем точки на график Плохая прямая!
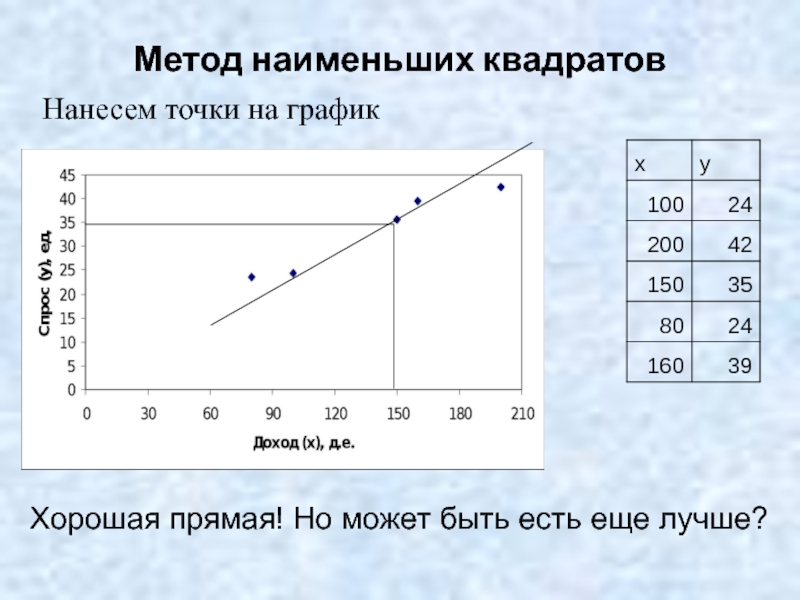
- 8. Метод наименьших квадратов Нанесем точки
- 9. Метод наименьших квадратов Нанесем точки
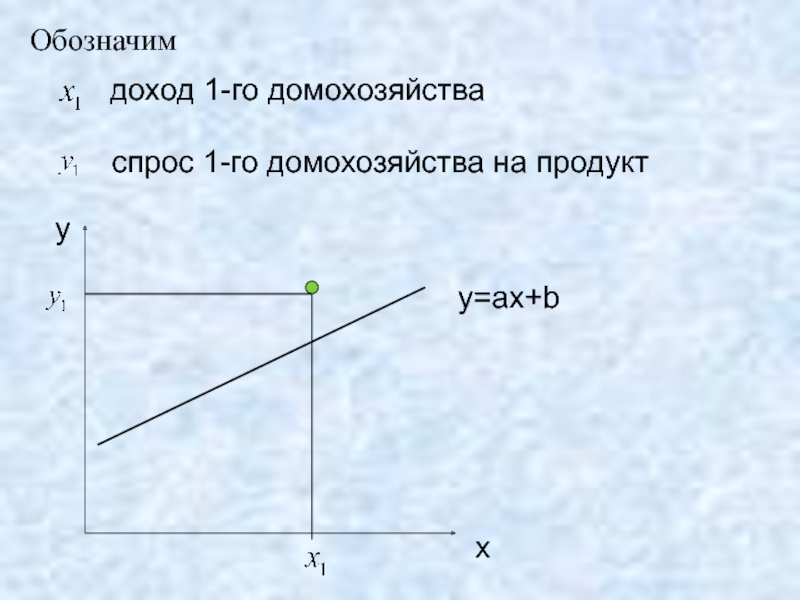
- 10. Обозначим доход 1-го
- 11. Обозначим доход 1-го
- 12. Обозначим доход 1-го
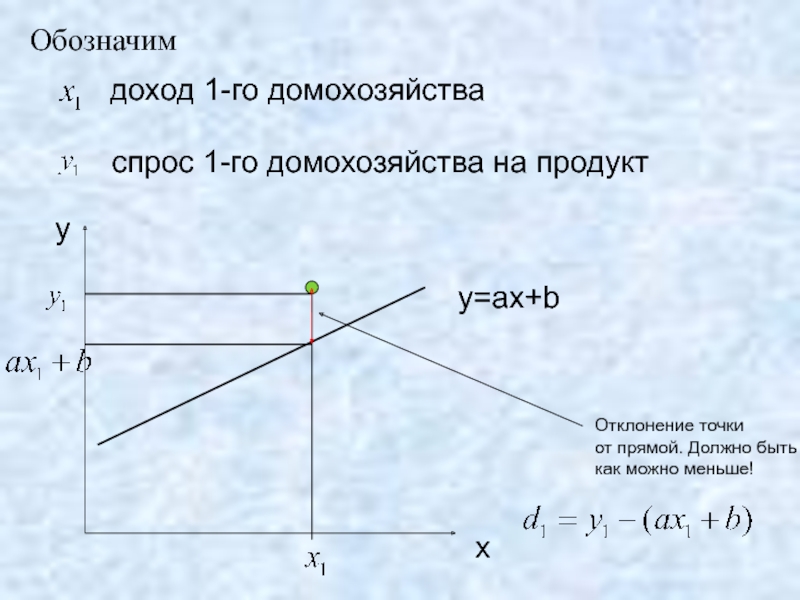
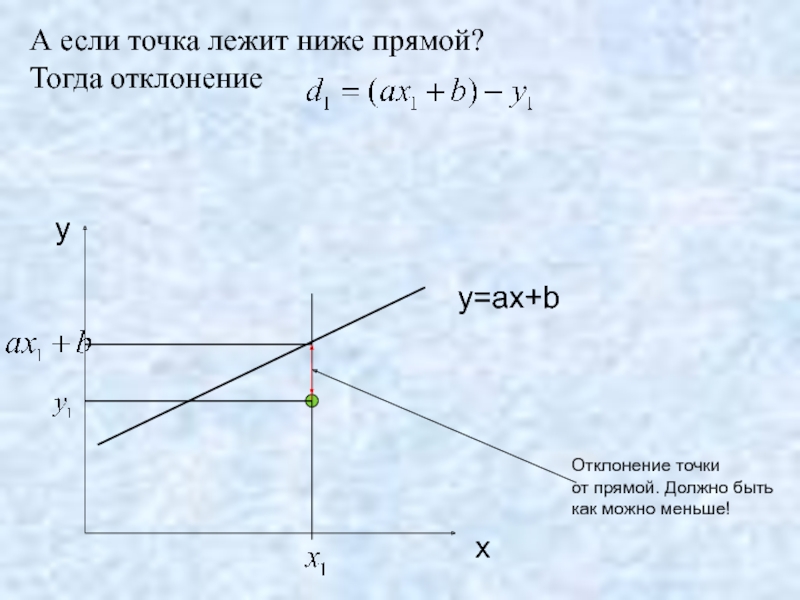
- 13. А если точка лежит ниже прямой? Тогда
- 14. Как учесть сразу оба случая? Квадрат отклонения
- 15. Квадрат отклонения до второй точки тоже должен быть как можно меньше.
- 16. Квадрат отклонения до второй точки тоже должен
- 17. Предположим, что у нас n точек. Тогда и для последней точки
- 18. Как учесть все точки сразу?
- 19. Как учесть все точки сразу?
- 20. Как учесть все точки сразу?
- 21. это просто числа, нам известные и
- 22. это просто числа, нам известные и
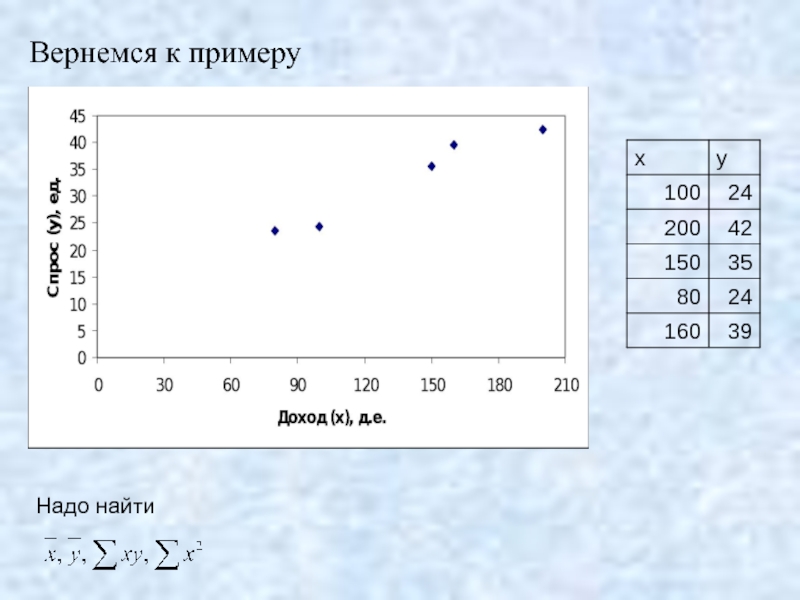
- 23. Вернемся к примеру Надо найти
- 24. Вернемся к примеру
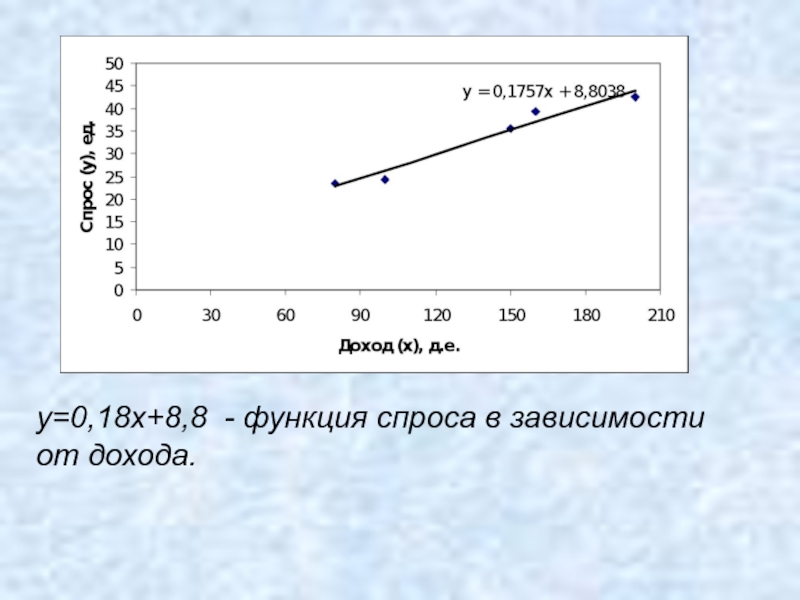
- 25. a=0,18, b=8,8 y=0,18x+8,8
- 26. y=0,18x+8,8 - функция спроса в зависимости от дохода.
- 27. y=0,18x+8,8 - функция спроса в зависимости от дохода.
- 28. y=0,18x+8,8 - функция спроса в
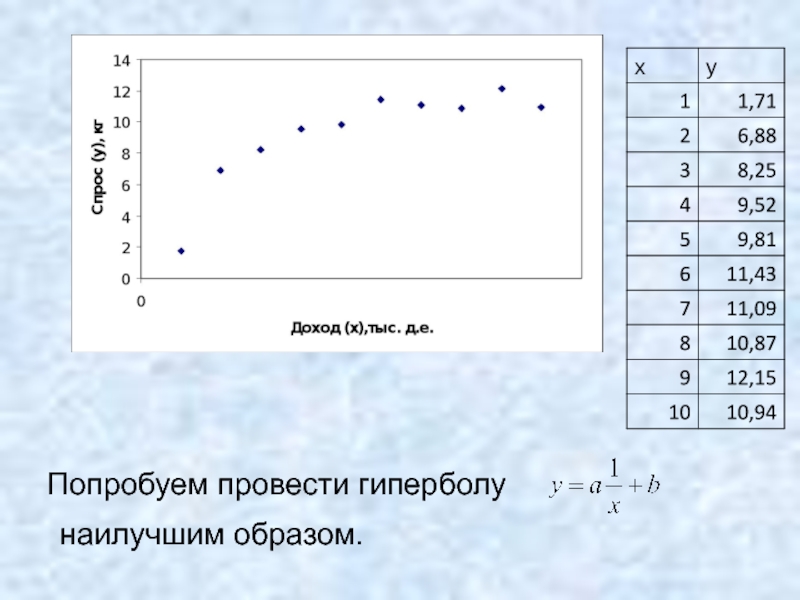
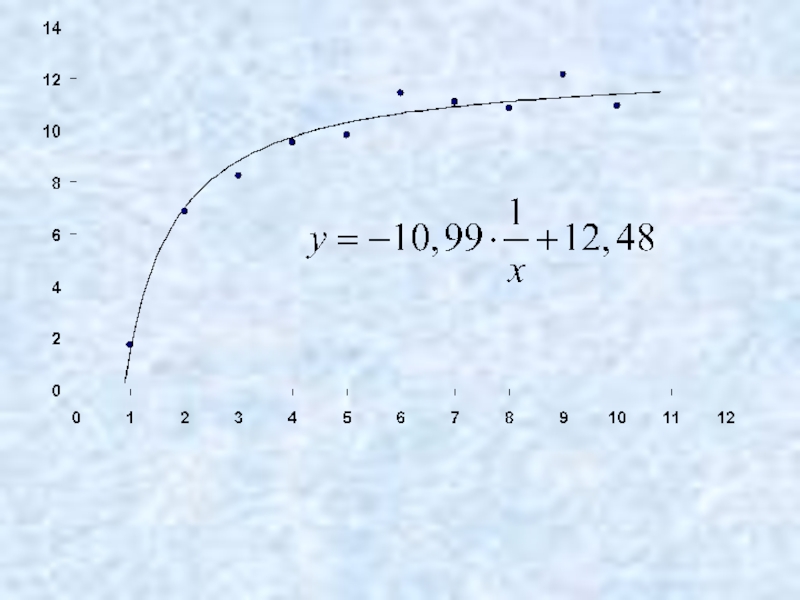
- 30. Зависимость нелинейная!
- 31. Попытка провести прямую
- 32. Попробуем провести гиперболу наилучшим образом.
- 33. Получили функцию двух переменных, для
- 34. Можно исследовать на экстремум, но лучше
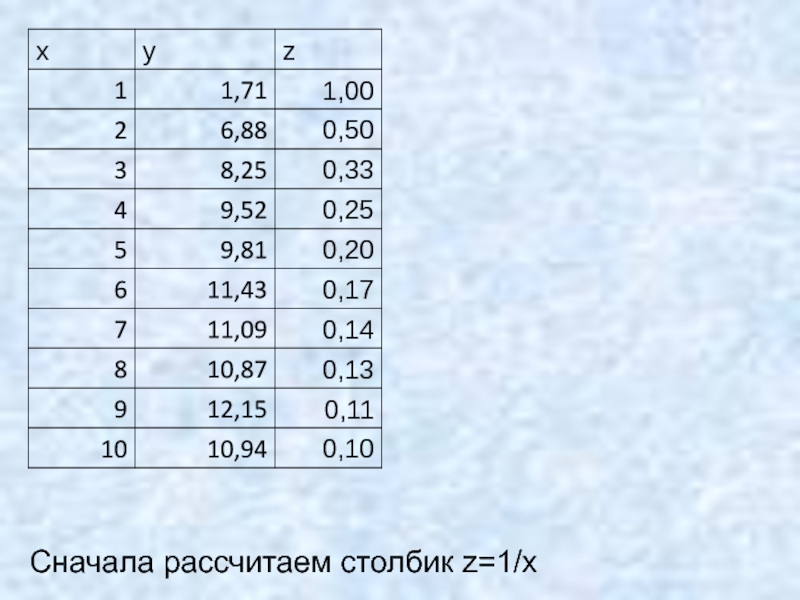
- 35. Сначала рассчитаем столбик z=1/x
- 39. y – зависимая или объясняемая переменная
- 40. Пример: Множественная регрессия Мы хотим определить связь
- 41. МОДЕЛЬ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ Для оценки необходима выборка (большое количество респондентов)
- 42. заработная плата i-го респондента n – объем
- 43. Чтобы подобрать наилучшие
- 44. Пример оценки параметров в модели зависимости заработной
- 46. ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ ЛИНЕЙНОЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИ Интерпретация: коэффициент
- 47. Пример оценки параметров в модели зависимости заработной
- 48. Пример оценки параметров в модели зависимости заработной
- 49. ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ ЛИНЕЙНОЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИ Пример y
- 50. ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ ЛИНЕЙНОЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИ При увеличении
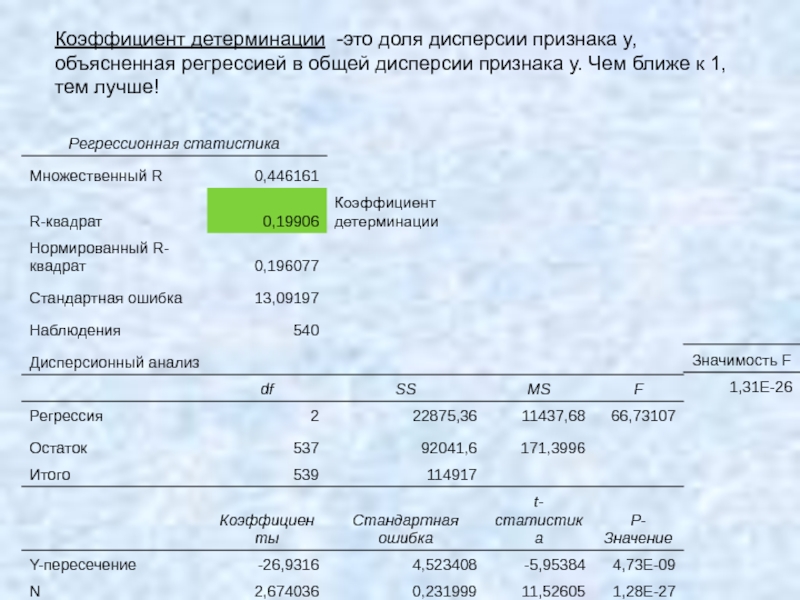
- 51. Коэффициент детерминации -это доля дисперсии признака y,
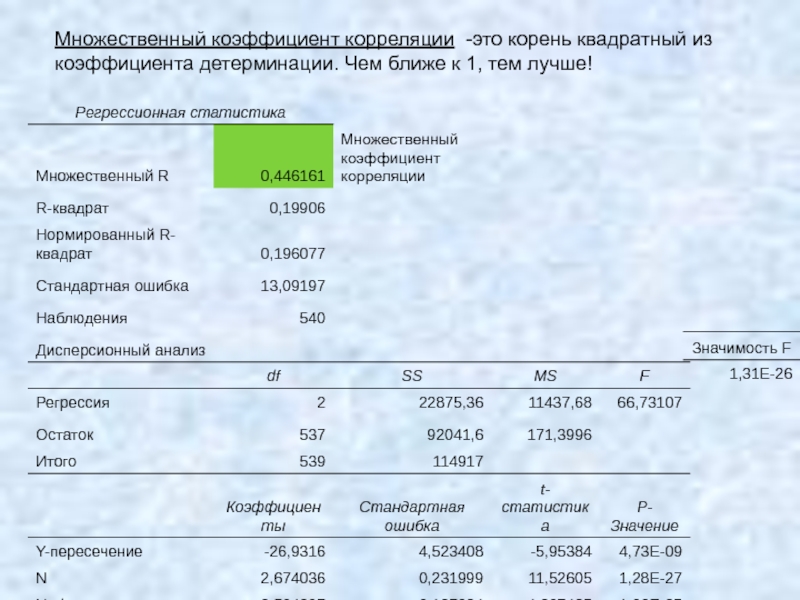
- 52. Множественный коэффициент корреляции -это корень квадратный из коэффициента детерминации. Чем ближе к 1, тем лучше!
- 53. Значимость F - это вероятность того, что
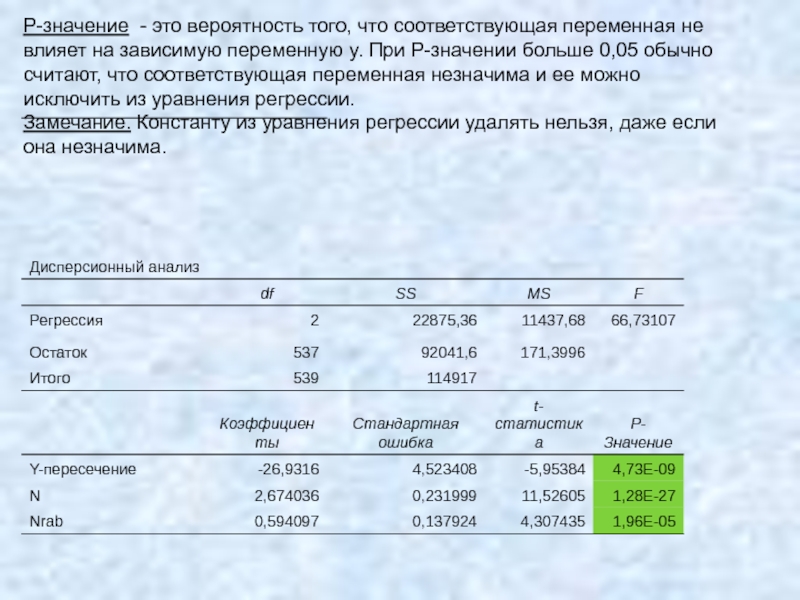
- 54. Р-значение - это вероятность того, что соответствующая
МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ Предположим, что необходимо получить функцию спроса на некоторый товар в зависимости от дохода. Проводится опрос домохозяйств. 1. Среднедушевой доход домохозяйства? 2.
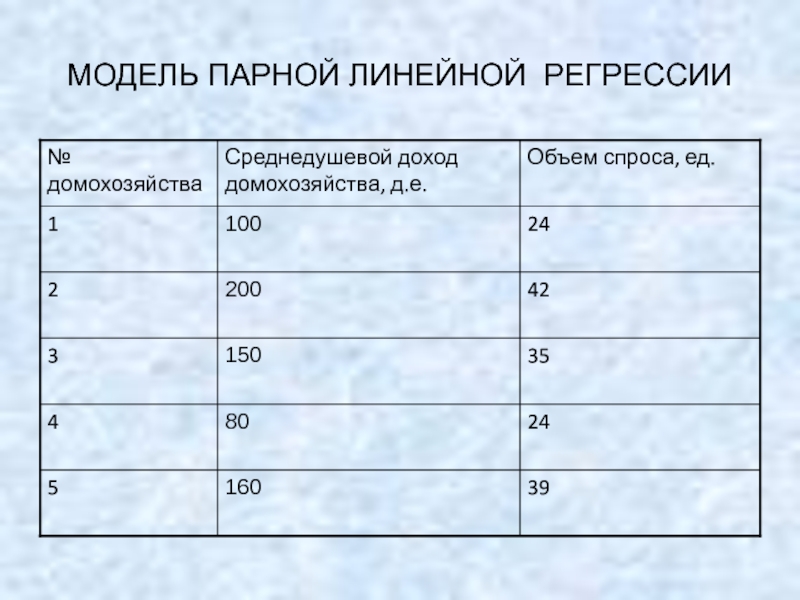
Слайд 1МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
y – зависимая (объясняемая) переменная
х – независимая (объясняющая)
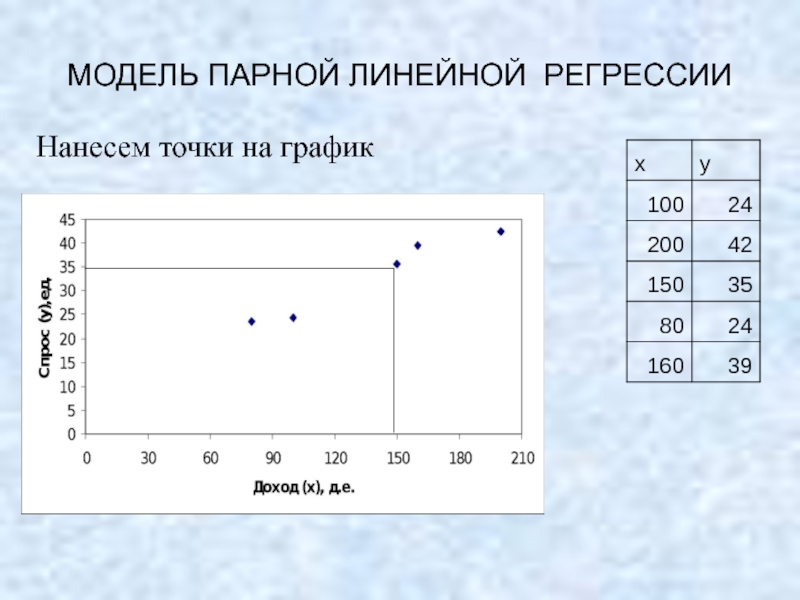
Слайд 2МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Предположим, что необходимо получить функцию
спроса на некоторый
товар в зависимости от дохода.
Проводится опрос домохозяйств.
1. Среднедушевой доход домохозяйства?
2. Сколько единиц товара приобрело домохозяйство за месяц?
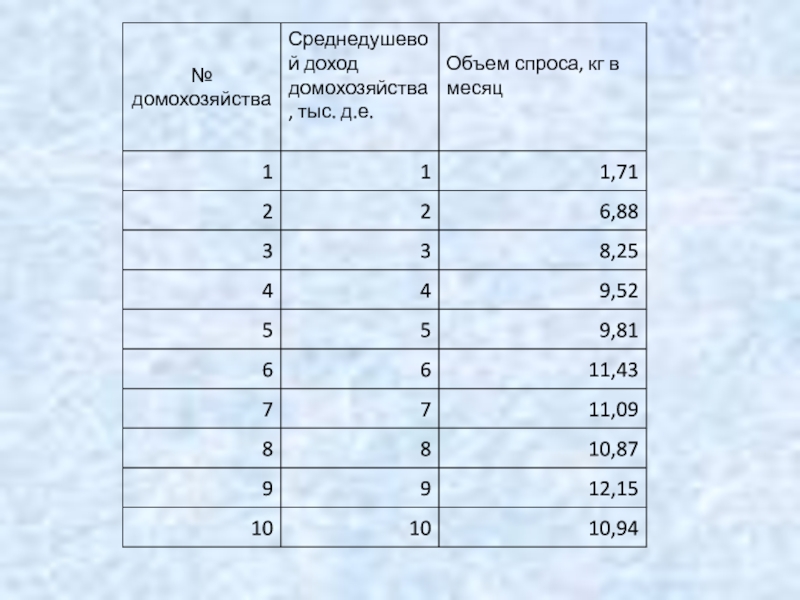
Проводится опрос домохозяйств.
1. Среднедушевой доход домохозяйства?
2. Сколько единиц товара приобрело домохозяйство за месяц?
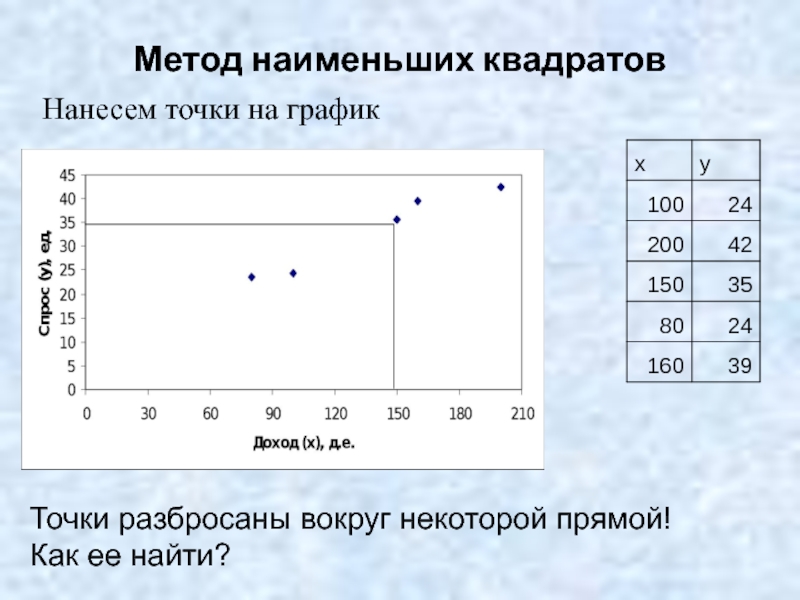
Слайд 5Метод наименьших квадратов
Нанесем точки на график
Точки разбросаны вокруг некоторой прямой!
Как ее
найти?
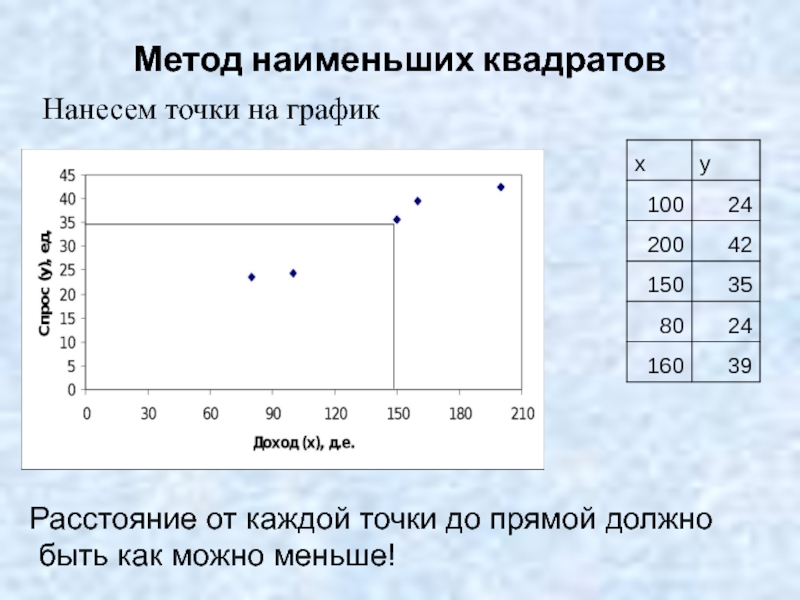
Слайд 6Метод наименьших квадратов
Нанесем точки на график
Расстояние от каждой точки до прямой
должно
быть как можно меньше!
быть как можно меньше!
Слайд 8Метод наименьших квадратов
Нанесем точки на график
Хорошая прямая! Но может быть есть
еще лучше?
Слайд 9Метод наименьших квадратов
Нанесем точки на график
Уравнение прямой в общем виде y=ax+b.
Надо
найти наиболее подходящие a и b.
найти наиболее подходящие a и b.
Слайд 11
Обозначим
доход 1-го домохозяйства
спрос 1-го домохозяйства на продукт
x
y
y=ax+b
Отклонение точки
от прямой.
Должно быть
как можно меньше!
как можно меньше!
Слайд 12
Обозначим
доход 1-го домохозяйства
спрос 1-го домохозяйства на продукт
x
y
y=ax+b
Отклонение точки
от прямой.
Должно быть
как можно меньше!
как можно меньше!
Слайд 13А если точка лежит ниже прямой?
Тогда отклонение
x
y
y=ax+b
Отклонение точки
от прямой.
Должно быть
как можно меньше!
как можно меньше!
Слайд 14Как учесть сразу оба случая?
Квадрат отклонения
должен быть как можно меньше.
x
y
y=ax+b
Отклонение точки
от прямой. Должно быть
как можно меньше!
Слайд 18Как учесть все точки сразу?
Сумма квадратов расстояний от точек до прямой
должна быть как можно меньше.
Слайд 19Как учесть все точки сразу?
Сумма квадратов расстояний от точек до прямой
должна быть как можно меньше.
обозначение
Слайд 20Как учесть все точки сразу?
Получили функцию двух переменных, для которой надо
найти минимум,
т.е. надо исследовать на экстремум.
т.е. надо исследовать на экстремум.
Слайд 28
y=0,18x+8,8 - функция спроса в зависимости
от дохода.
Выполнить прогноз потребления продукта
домохозяйством с доходом 200 д.е.
2)Найти предельную склонность к потреблению
продукта.
3) Найти эластичность спроса по доходу при
доходе 100 д.е. и 50 д.е.
Слайд 33
Получили функцию двух переменных, для которой надо найти минимум,
т.е. надо исследовать
на экстремум.
Слайд 34
Можно исследовать на экстремум, но лучше заменить
тогда
А это такая же функция,
что и для линейной регрессии!
Поэтому можно воспользоваться готовым результатом!
Поэтому можно воспользоваться готовым результатом!
Слайд 38
- функция спроса в зависимости
от дохода.
Выполнить прогноз потребления продукта
домохозяйством с доходом 4 тыс.д.е.
2) Имеется ли уровень насыщения для данного
продукта? Если да, найти его.
2)Найти предельную склонность к потреблению
продукта.
3) Найти эластичность спроса по доходу при
доходе 1000 д.е. и 10000 д.е.
от дохода.
Выполнить прогноз потребления продукта
домохозяйством с доходом 4 тыс.д.е.
2) Имеется ли уровень насыщения для данного
продукта? Если да, найти его.
2)Найти предельную склонность к потреблению
продукта.
3) Найти эластичность спроса по доходу при
доходе 1000 д.е. и 10000 д.е.
Слайд 39y – зависимая или объясняемая переменная
- независимые или объясняющие переменные
- случайная составляющая.
Задача множественного регрессионного анализа – оценить
- случайная составляющая.
Задача множественного регрессионного анализа – оценить
МОДЕЛЬ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Слайд 40Пример:
Множественная регрессия
Мы хотим определить связь между заработной платой, числом лет обучения
и опытом работы.
y – почасовая заработная плата ($).
x1 – число лет обучения
x2 – опыт работы (лет)
y – почасовая заработная плата ($).
x1 – число лет обучения
x2 – опыт работы (лет)
Слайд 41МОДЕЛЬ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Для оценки необходима выборка (большое количество респондентов)
Слайд 42заработная плата i-го респондента
n – объем выборки
число лет обучения i-го респондента
опыт
работы i-го респондента
Слайд 44Пример оценки параметров в модели зависимости заработной платы от числа лет
обучения и опыта работы
Zpl = 2.67*N + 0.59*NRab -26.93
Слайд 46ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ ЛИНЕЙНОЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Интерпретация: коэффициент регрессии при переменной xi показывает
на сколько единиц изменится переменная y при изменении переменной xi на 1 единицу, при условии постоянства других переменных:
Слайд 47Пример оценки параметров в модели зависимости заработной платы от числа лет
обучения и опыта работы
Zpl = 2.67*N + 0.59*NRab -26.93
Слайд 48Пример оценки параметров в модели зависимости заработной платы от числа лет
обучения и опыта работы
Zpl = 2.67*N + 0.59*NRab -26.93
Каждый дополнительный год обучения при данном опыте работы увеличивает
часовой заработок на 2,67$
Каждый дополнительный год опыта работы при данной продолжительности
обучения увеличивает часовой заработок на 0,59$
-26,93 не имеет содержательной интерпретации.
Слайд 49ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ ЛИНЕЙНОЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Пример y – затраты на питание (млрд.
$)
x1 – личный располагаемый доход (млрд. $)
x2 – индекс цен на продукты питания (%)
x1 – личный располагаемый доход (млрд. $)
x2 – индекс цен на продукты питания (%)
Слайд 50ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ ЛИНЕЙНОЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
При увеличении личного располагаемого дохода на 1
млрд. $ (при сохранении неизменной цены) расходы на питание увеличатся на 112 млн.$
При увеличении индекса цен на 1 процентный пункт (при сохранении постоянных доходов) расходы на питание сократятся на 739 млн.$
116,7 не интерпретируется, т.к. x1 и x2 не могут быть равными 0.
При увеличении индекса цен на 1 процентный пункт (при сохранении постоянных доходов) расходы на питание сократятся на 739 млн.$
116,7 не интерпретируется, т.к. x1 и x2 не могут быть равными 0.
Пример y – затраты на питание (млрд. $)
x1 – личный располагаемый доход (млрд. $)
x2 – индекс цен на продукты питания (%)
Слайд 51Коэффициент детерминации -это доля дисперсии признака y, объясненная регрессией в общей
дисперсии признака y. Чем ближе к 1, тем лучше!
Слайд 52Множественный коэффициент корреляции -это корень квадратный из коэффициента детерминации. Чем ближе
к 1, тем лучше!
Слайд 53Значимость F - это вероятность того, что полученная зависимость случайна. При
значимости больше 0,05 обычно считают, что построенная зависимость незначима. Моделью нельзя пользоваться для прогнозирования.
Слайд 54Р-значение - это вероятность того, что соответствующая переменная не влияет на
зависимую переменную y. При Р-значении больше 0,05 обычно считают, что соответствующая переменная незначима и ее можно исключить из уравнения регрессии.
Замечание. Константу из уравнения регрессии удалять нельзя, даже если она незначима.
Замечание. Константу из уравнения регрессии удалять нельзя, даже если она незначима.
