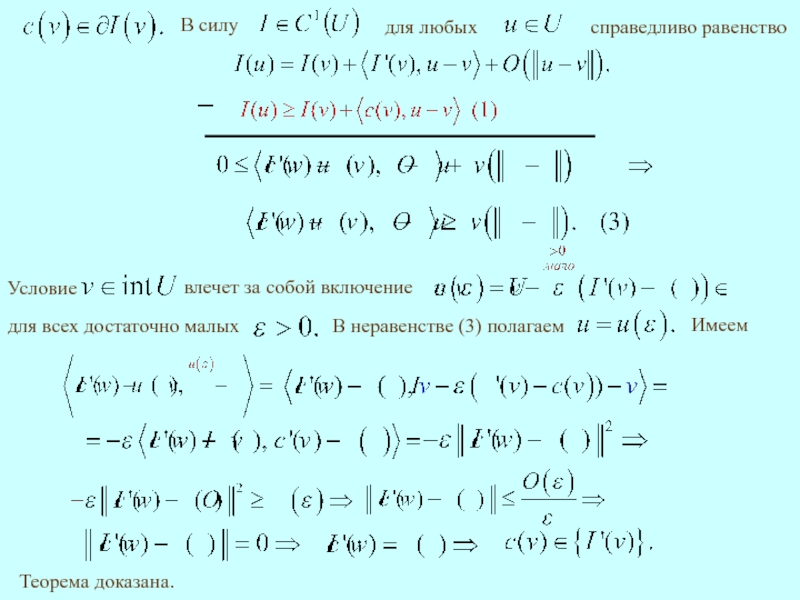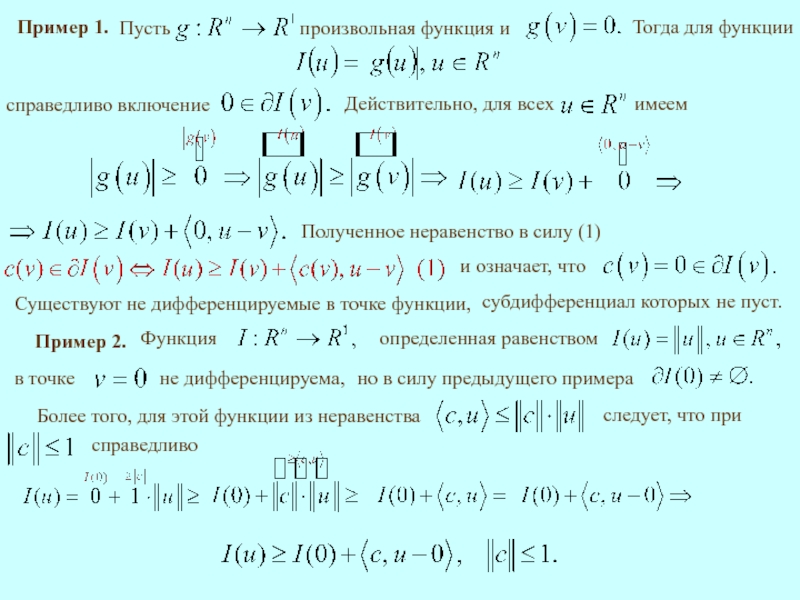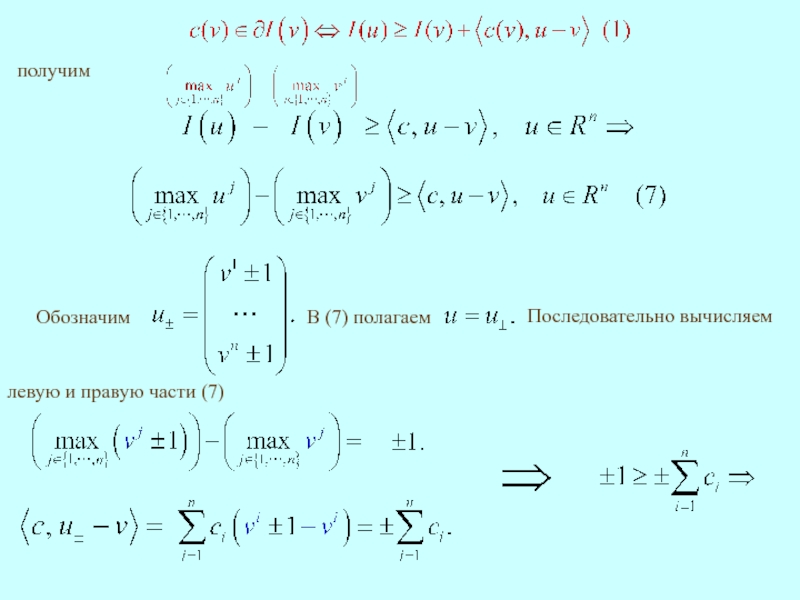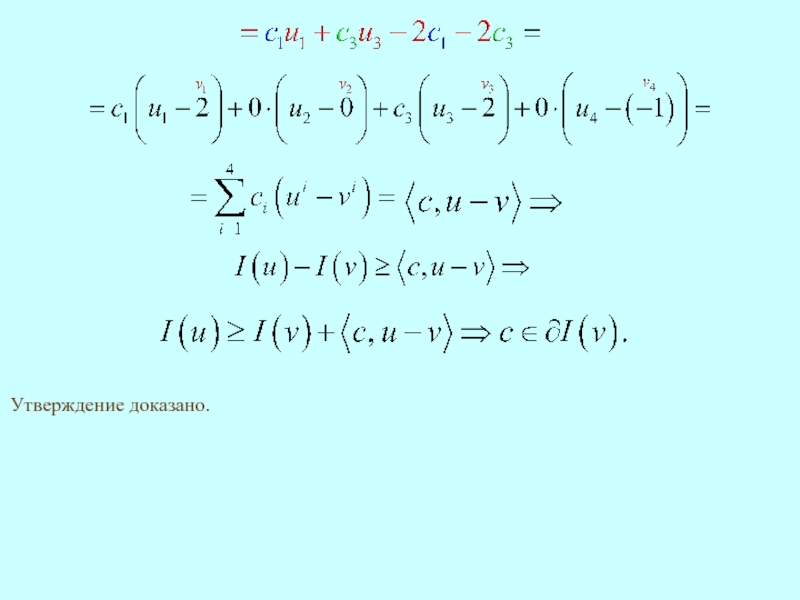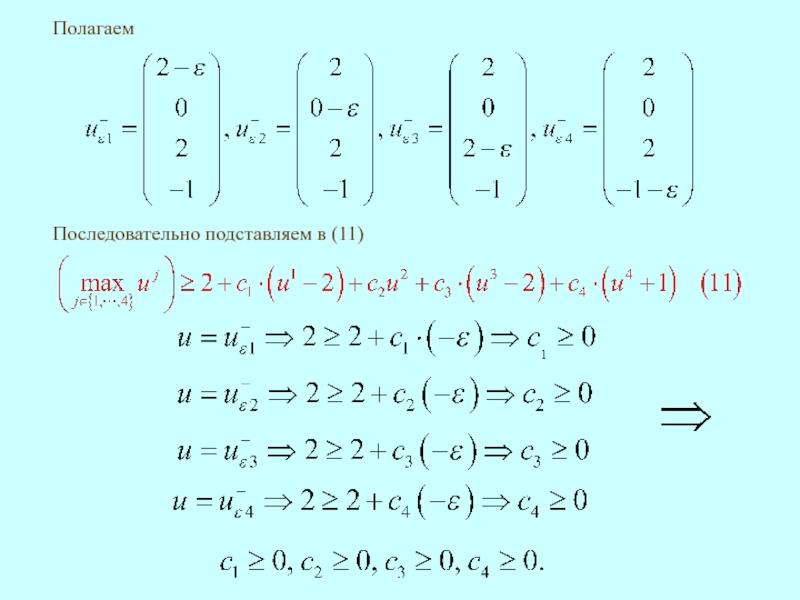- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклый анализ. Субградиент и субдифференциал функции. Лекция 20 презентация
Содержание
- 1. Выпуклый анализ. Субградиент и субдифференциал функции. Лекция 20
- 2. 7. СУБГРАДИЕНТ И СУБДИФФЕРЕНЦИАЛ
- 6. Пример 1. Тогда для функции
- 7. Таким образом, справедливо вложение Упражнение. Решение. Требуемое неравенство имеет место.
- 9. Упражнение. Решение. Тогда Пример 3.
- 11. Докажем обратное вложение Тогда
- 16. Упражнение. Решение.
- 17. Утверждение доказано.
- 19. Обозначим: Из (12) и (13) следует
- 20. Полагаем Последовательно подставляем в (11)
- 21. Утверждение доказано. Полагаем Последовательно подставляем в (11)
- 22. Упражнение. Решение.
7. СУБГРАДИЕНТ И СУБДИФФЕРЕНЦИАЛ ФУНКЦИИ 7.1. Определение субградиента и субдифференциала функции. Примеры.
Слайд 2
7. СУБГРАДИЕНТ И СУБДИФФЕРЕНЦИАЛ ФУНКЦИИ
7.1. Определение субградиента и субдифференциала функции.
Примеры.
Слайд 3
7.1. Определение субградиента и субдифференциала функции. Примеры.
Определение 1.
если
Геометрический
смысл неравенства (1) состоит в том,
Однако естественным это понятие является для выпуклых функций.
7. СУБГРАДИЕНТ И СУБДИФФЕРЕНЦИАЛ ФУНКЦИИ
Слайд 4
Для выпуклых дифференцируемых функций был установлен критерий выпуклости
Для таких функций
неравенство (1)
Из сказанного выше следует, что субдифференциал гладких выпуклых функций не пуст,
а градиенты этих функций суть их субградиенты.
Теорема 1.
то
Доказательство.
Вложение
следует непосредственно из неравенства (2).
Докажем обратное вложение.
Пусть
Слайд 6
Пример 1.
Тогда для функции
Существуют не дифференцируемые в точке функции,
субдифференциал которых не пуст.
Пример 2.
Более того, для этой функции из неравенства
