- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники презентация
Содержание
- 1. Многогранники
- 2. Содержание Призма Параллелепипед Пирамида Далее
- 3. Призма Две грани которого являются (равными) многоугольниками, лежащими
- 4. Параллелепипед Призма, основанием которой служит параллелограмм, или (равносильно)
- 5. Пирамида Многогранник, одна из граней которого
- 6. Наклонная Призма боковые ребра которой не перпендикулярны
- 7. Правильная Правильная призма — это прямая призма, основанием
- 8. Прямая Прямой призмой называют призму, боковые ребра
- 9. Прямой В основании лежит параллелограмм , а
- 10. Прямоугольный Прямоугольный параллелепипед - это прямой параллелепипед,
- 11. Наклонный Все его грани – параллелограммы, а
- 12. Правильная Пирамида называется правильной, если основанием её
- 13. Усеченная правильная Усеченной пирамидой называется многогранник, у которого
- 14. Неправильная Пирамида называется неправильной, если в её
Содержание Призма Параллелепипед Пирамида Далее
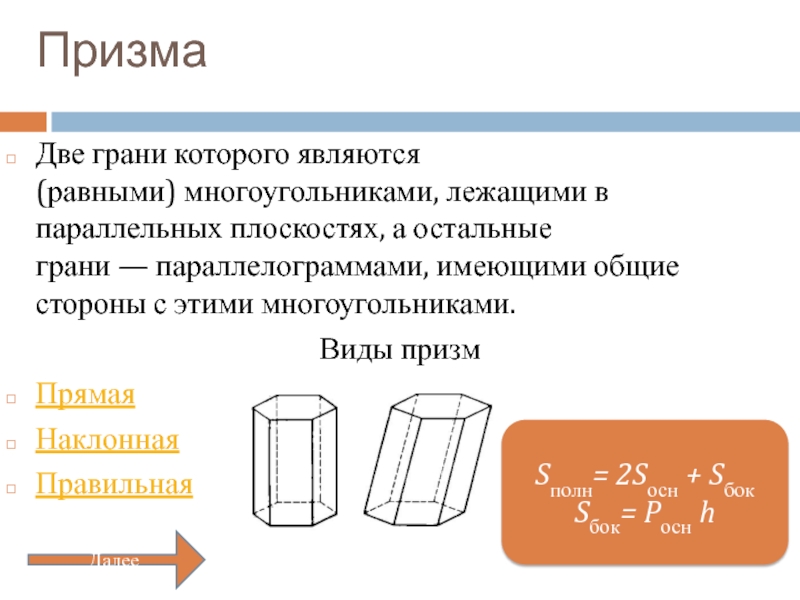
Слайд 3Призма
Две грани которого являются (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные
грани — параллелограммами, имеющими общие стороны с этими многоугольниками.
Виды призм
Прямая
Наклонная
Правильная
Виды призм
Прямая
Наклонная
Правильная
Sполн= 2Sосн + Sбок
Sбок= Pосн h
Далее
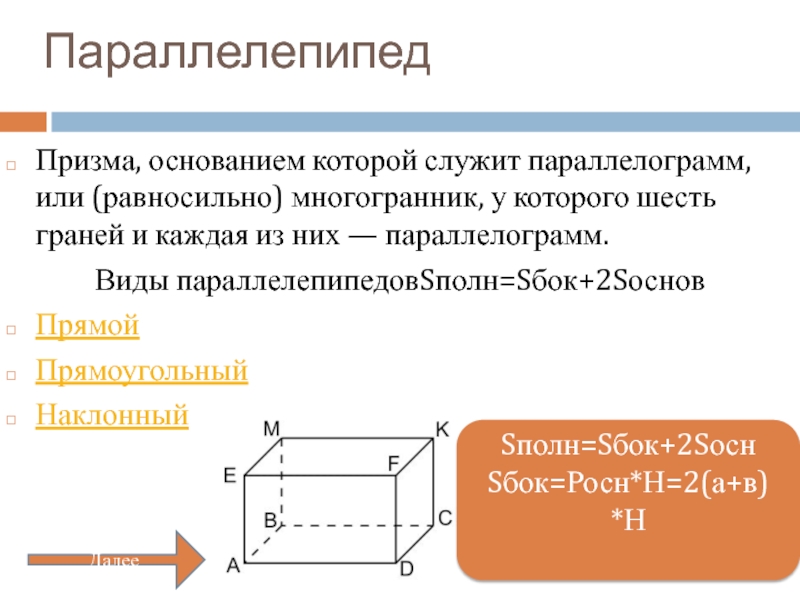
Слайд 4Параллелепипед
Призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней
и каждая из них — параллелограмм.
Виды параллелепипедовSполн=Sбок+2Sоснов
Прямой
Прямоугольный
Наклонный
Виды параллелепипедовSполн=Sбок+2Sоснов
Прямой
Прямоугольный
Наклонный
Sполн=Sбок+2Sосн
Sбок=Росн*Н=2(а+в) *Н
Далее
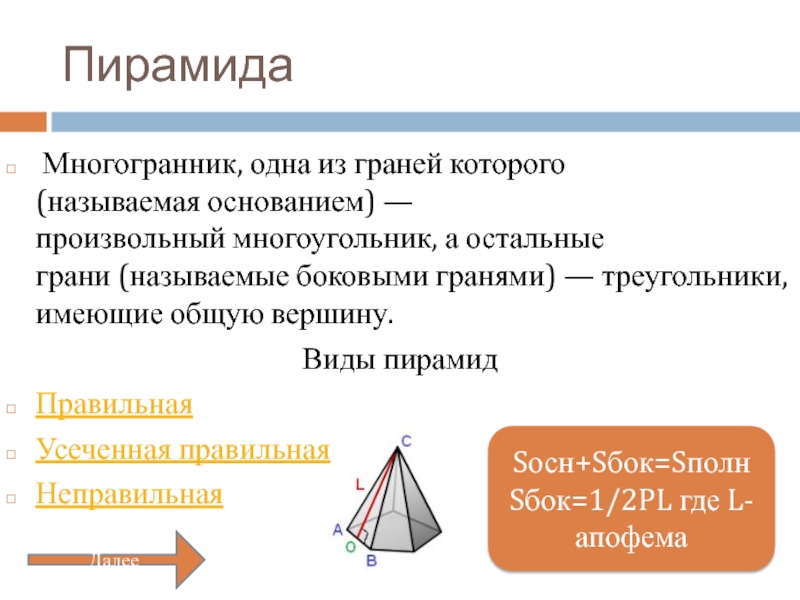
Слайд 5Пирамида
Многогранник, одна из граней которого
(называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину.
Виды пирамид
Правильная
Усеченная правильная
Неправильная
Виды пирамид
Правильная
Усеченная правильная
Неправильная
Sосн+Sбок=Sполн
Sбок=1/2PL где L-апофема
Далее
Слайд 6Наклонная
Призма боковые ребра которой не перпендикулярны основанию.
Свойства
Боковые рёбра не перпендикулярны
В основании
лежат произвольные многоугольники
Слайд 7Правильная
Правильная призма — это прямая призма, основанием которой является правильный многоугольник.
Свойства
Основания правильной призмы являются правильными многоугольниками.
Боковые грани правильной призмы являются равными прямоугольниками.
Боковые ребра правильной призмы равны.
Слайд 8Прямая
Прямой призмой называют призму, боковые ребра которой перпендикулярны к плоскостям оснований.
Свойства
Все боковые грани прямой призмы являются прямоугольниками.
Высота прямой призмы равна длине бокового ребра.
Боковые ребра перпендикулярны плоскостям.
Высота прямой призмы равна длине бокового ребра.
Боковые ребра перпендикулярны плоскостям.
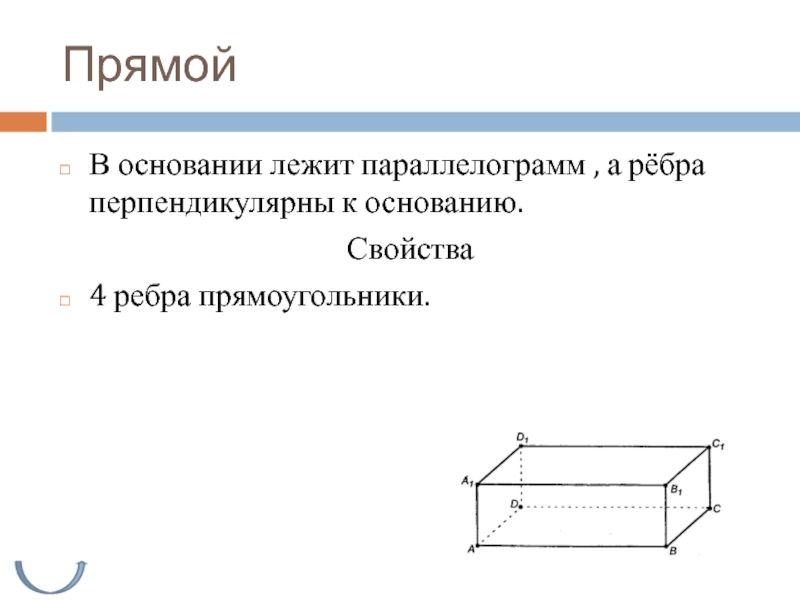
Слайд 9Прямой
В основании лежит параллелограмм , а рёбра перпендикулярны к основанию.
Свойства
4 ребра
прямоугольники.
Слайд 10Прямоугольный
Прямоугольный параллелепипед - это прямой параллелепипед, в основании которого прямоугольник.
Свойства
Примерами прямоугольного
параллелепипеда служат классная комната, кирпич, спичечный коробок или системный блок компьютера.
Длины трёх рёбер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями. Прямоугольный параллелепипед с равными измерениями называется кубом. Все шесть граней куба — равные квадраты.
Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Длины трёх рёбер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями. Прямоугольный параллелепипед с равными измерениями называется кубом. Все шесть граней куба — равные квадраты.
Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Слайд 11Наклонный
Все его грани – параллелограммы, а противоположные грани — равные параллелограммы.
Свойства
Диагонали параллелепипеда
пересекаются в одной точке и делятся в этой точки пополам.
Слайд 12Правильная
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется
в центр основания. Тогда она обладает такими свойствами:
Свойства
боковые рёбра правильной пирамиды равны;
в правильной пирамиде все боковые грани — конгруэнтные равнобедренные треугольники;
в любую правильную пирамиду можно как вписать, так и описать вокруг неё сферу;
если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна , а каждый из них соответственно , где n — количество сторон многоугольника основания;
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Свойства
боковые рёбра правильной пирамиды равны;
в правильной пирамиде все боковые грани — конгруэнтные равнобедренные треугольники;
в любую правильную пирамиду можно как вписать, так и описать вокруг неё сферу;
если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна , а каждый из них соответственно , где n — количество сторон многоугольника основания;
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Слайд 13Усеченная правильная
Усеченной пирамидой называется многогранник, у которого вершинами служат вершины основания и
вершины ее сечения плоскостью, параллельной основанию.
Свойства
Основания усеченной пирамиды — подобные многоугольники.
Боковые грани усеченной пирамиды — трапеции.
Боковые ребра правильной усеченной пирамиды равны и одинаково наклонены к основанию пирамиды.
Боковые грани правильной усеченной пирамиды — равные между собой равнобедренные трапеции и одинаково наклонены к основанию пирамиды.
Двугранные углы при боковых ребрах правильной усеченной пирамиды равны.
Свойства
Основания усеченной пирамиды — подобные многоугольники.
Боковые грани усеченной пирамиды — трапеции.
Боковые ребра правильной усеченной пирамиды равны и одинаково наклонены к основанию пирамиды.
Боковые грани правильной усеченной пирамиды — равные между собой равнобедренные трапеции и одинаково наклонены к основанию пирамиды.
Двугранные углы при боковых ребрах правильной усеченной пирамиды равны.
Слайд 14Неправильная
Пирамида называется неправильной, если в её основании лежит неправильный многоугольник ,
или если в основании правильный многоугольник, но вершина пирамиды не проектируется в центр основания.
