Some terminology
Direct argument
Contrapositive argument
Proof by contradiction
Mathematical induction
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Methods of proof презентация
Содержание
- 1. Methods of proof
- 2. Some terminology A theorem is a statement
- 3. Терминология We demonstrate that a theorem is
- 4. Some terminology The statements used in a
- 5. Some terminology Axioms may be stated using
- 6. Some terminology Rules of inference, together with
- 7. Some terminology A less important theorem that
- 8. Some terminology A corollary is a theorem
- 9. Some terminology A conjecture is a statement
- 10. Methods of proof In practice, the proofs
- 11. Methods of proof Informal proofs can often
- 12. Methods of proof The methods of proof
- 13. Methods of proof Consequently, understanding the techniques
- 14. Methods of proof
- 15. Methods of proof There are several standard
- 16. Direct argument
- 17. Contrapositive argument
- 18. Proof by contradiction
- 19. Example 1 Use a direct method of
- 20. Example 2 Let n be a positive
- 21. Example 3 Use a proof by contradiction
- 22. Example 3 Use a proof by contradiction
- 23. Mathematical induction In computing a program is
- 24. Mathematical induction Consider the following recursive algorithm,
- 25. Mathematical induction To see how the algorithm
- 26. Mathematical induction
- 27. Mathematical induction So does the algorithm for
- 28. Mathematical induction By condition 1) the algorithm
- 29. Mathematical induction
- 30. Mathematical induction
- 31. Mathematical induction
- 32. Mathematical induction
- 33. Mathematical induction
- 34. Mathematical induction Example 3 A sequence
- 35. Mathematical induction
Слайд 1 Methods of proof
Слайд 2Some terminology
A theorem is a statement that can be shown to
In mathematical writing, the term theorem is usually reserved for a statement that is considered at least somewhat important.
Less important theorems sometimes are called propositions.
A theorem may be the universal quantification of a conditional statement with one or more premises and a conclusion.
Слайд 3Терминология
We demonstrate that a theorem is true with a proof.
A
Some terminology
Слайд 4Some terminology
The statements used in a proof can include
axioms (or
the premises, if any, of the theorem,
and previously proven theorems.
Слайд 5Some terminology
Axioms may be stated using primitive terms that do not
Слайд 6Some terminology
Rules of inference, together with definitions of terms, are used
Слайд 7Some terminology
A less important theorem that is helpful in the proof
Complicated proofs are usually easier to understand when they are proved using a series of lemmas, where each lemma is proved individually.
Слайд 8Some terminology
A corollary is a theorem that can be established directly
Слайд 9Some terminology
A conjecture is a statement that is being proposed to
When a proof of a conjecture is found, the conjecture becomes a theorem. Many times conjectures are shown to be false, so they are not theorems.
Слайд 10Methods of proof
In practice, the proofs of theorems designed for human
where more than one rule of inference may be used in each step, where steps may be skipped,
where the axioms being assumed and the rules of inference used are not explicitly stated.
Слайд 11Methods of proof
Informal proofs can often explain to humans why theorems
Слайд 12Methods of proof
The methods of proof discussed here are important not
These applications include
verifying that computer programs are correct, establishing that operating systems are secure,
making inferences in artificial intelligence,
showing that system specifications are consistent, and so on.
Слайд 13Methods of proof
Consequently, understanding the techniques used in proofs is essential
Слайд 15Methods of proof
There are several standard methods of proof, including the
direct argument,
contrapositive argument,
proof by contradiction.
Слайд 19Example 1 Use a direct method of proof to show that
Слайд 20Example 2 Let n be a positive integer. Prove, using the
Слайд 21Example 3 Use a proof by contradiction to show that if
Solution
By way of contradiction, assume that х is a fraction and write х = m/n where n and m are integers, n is not equal to 0 and n and m have no common factors. Since x2 = 2, we have that (m/n)2 = 2. Therefore, m2 = 2 n2. But this implies that m2 is an even integer. Therefore, т is an even integer. Hence, т = 2р for some other integer р.
Слайд 23Mathematical induction
In computing a program is said to be correct if
Proving the correctness of algorithms containing loops requires a powerful method of proof called mathematical induction.
Слайд 24Mathematical induction
Consider the following recursive algorithm, intended to calculate the maximum
begin
г:=0;
М:=0;
while г < n do
begin
r :=r+1;
M:=max(M, ar);
end
еnd
Слайд 25Mathematical induction
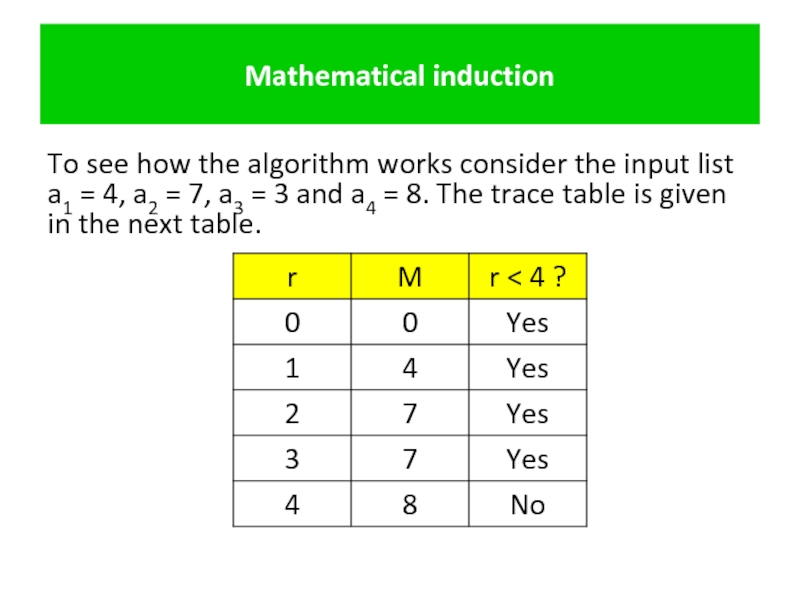
To see how the algorithm works consider the input list
Слайд 26Mathematical induction
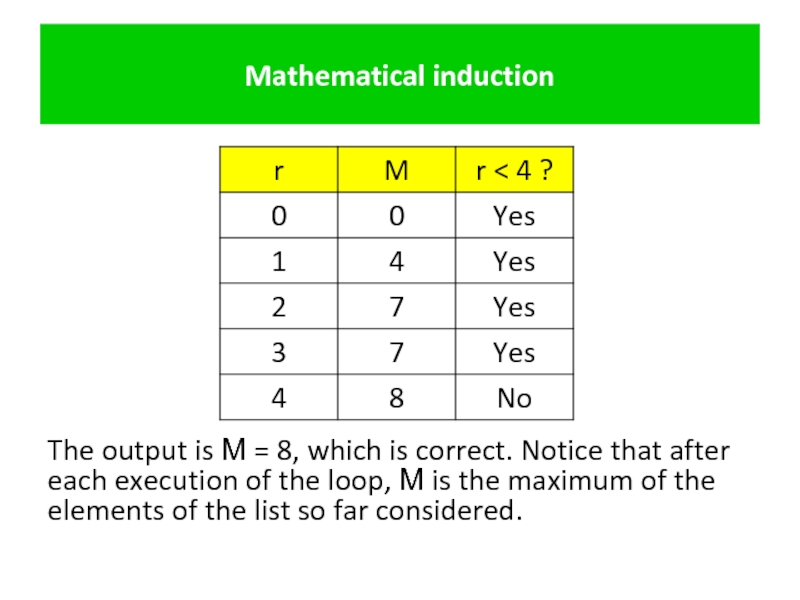
The output is М = 8, which is correct. Notice
Слайд 27Mathematical induction
So does the algorithm for all lists of any length
Consider an input a1, a2, …, an of length n and let Mk be the value of М after k executions of the loop.
For an input list a1 of length 1, the loop is executed once and M is assigned to be the maximum of 0 and a1,which is just a1. It is the correct input.
If after k executions of the loop, Mk is the maximum element of the list a1, a2, …, ak then after one more loop Mk+1 is assigned the value max(Mk, ak+1 ) which will then be the maximum element of the list a1, a2, …, ak+1.
Слайд 28Mathematical induction
By condition 1) the algorithm works for any list of
This process can be formalised as follows.
Слайд 34Mathematical induction
Example 3
A sequence of integers x1, x2, …, xn
x1 = 1 and xk+1 = xk + 8k for к >= 1.
Prove that
xn = (2n – 1)2 for all n >= 1.
Solution
Let Р(n) be the predicate xn = (2n – 1)2. In the case n = 1, (2n – 1)2 = (2 • 1 – 1)2 = 1. Therefore, Р(1) is true.