- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
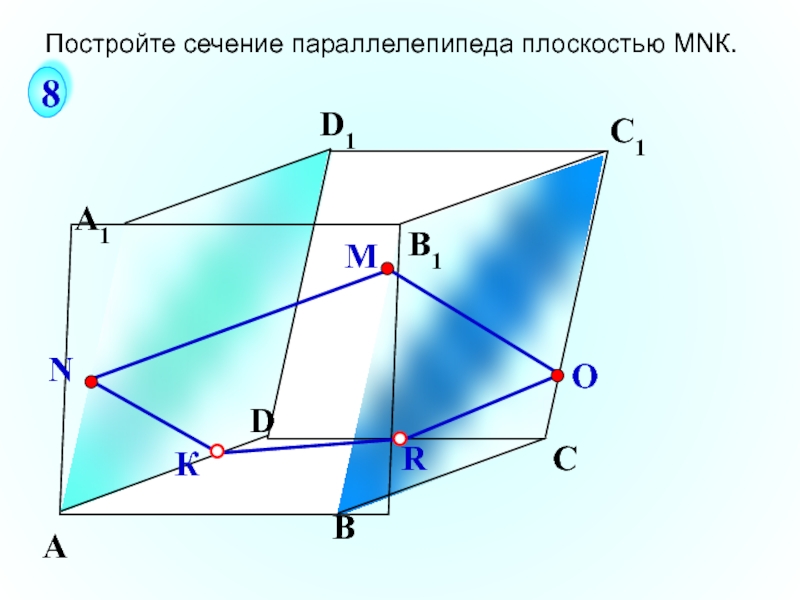
Построение сечений многогранника презентация
Содержание
- 1. Построение сечений многогранника
- 2. Построить сечение многогранника плоскостью –
- 3. А В
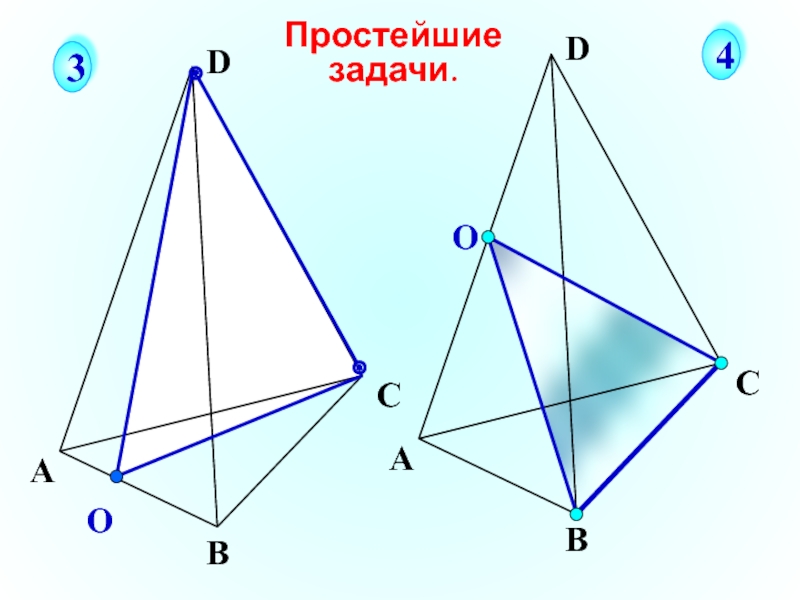
- 4. О А В С D
- 5. А В С
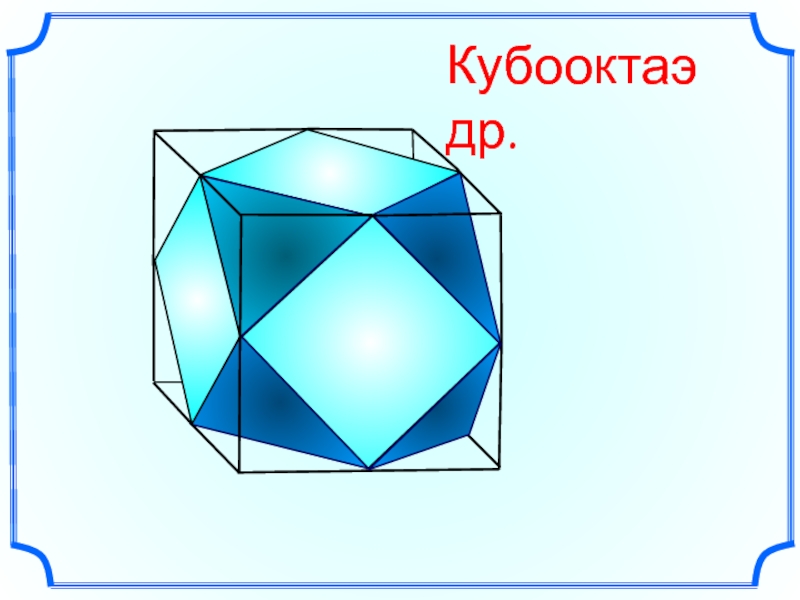
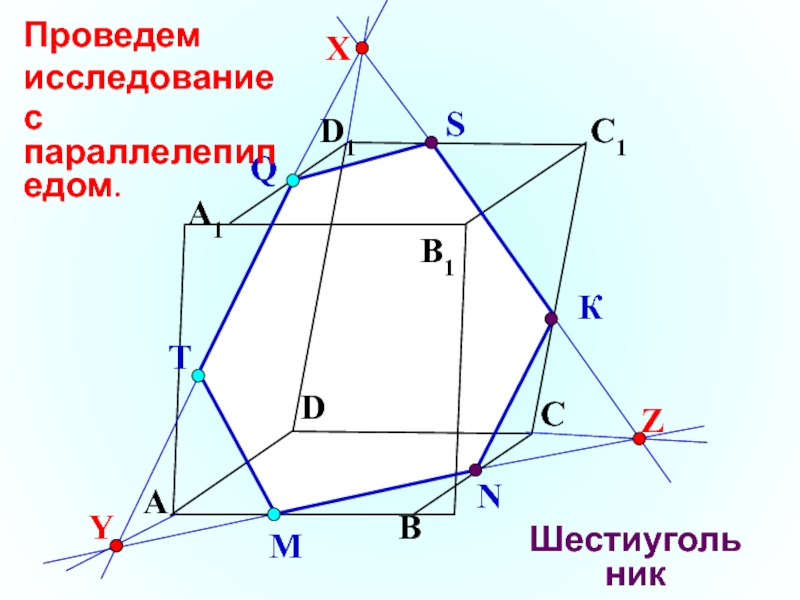
- 6. Кубооктаэдр.
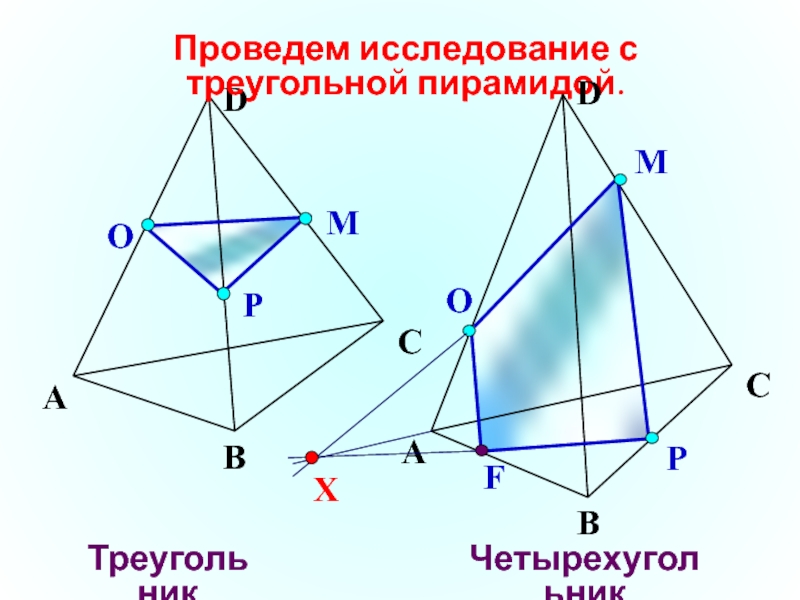
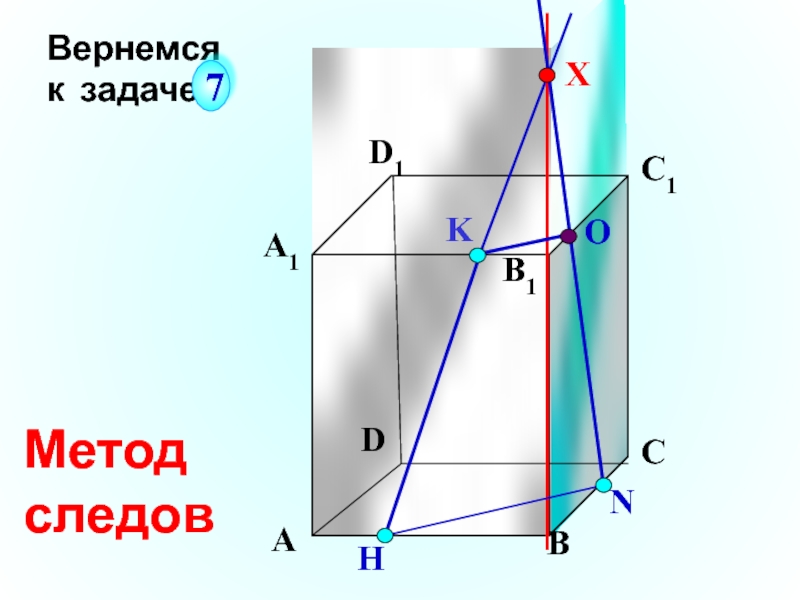
- 7. Р Проведем исследование
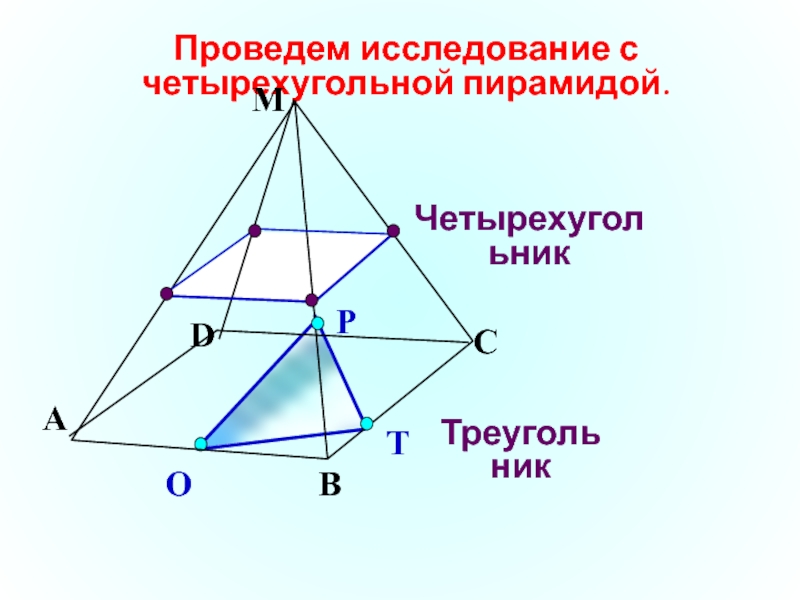
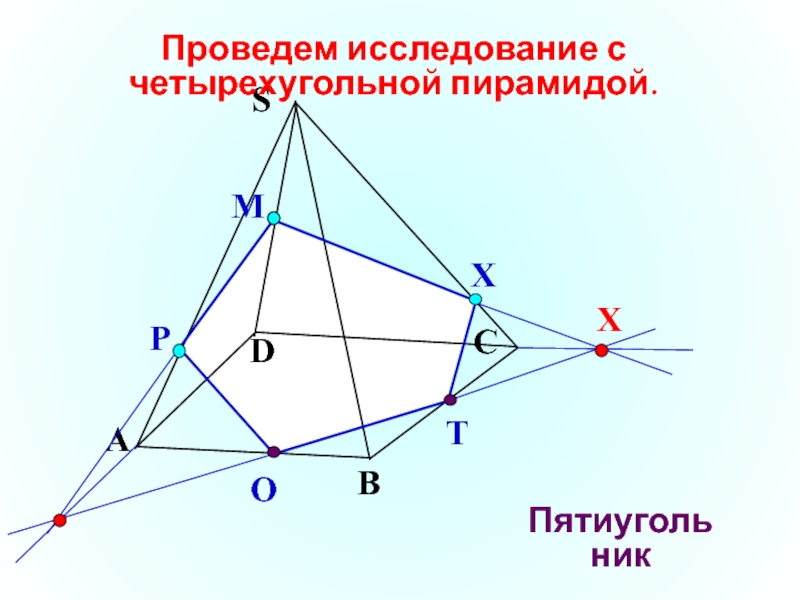
- 8. Проведем исследование с четырехугольной пирамидой.
- 9. О Т А
- 10. А В С
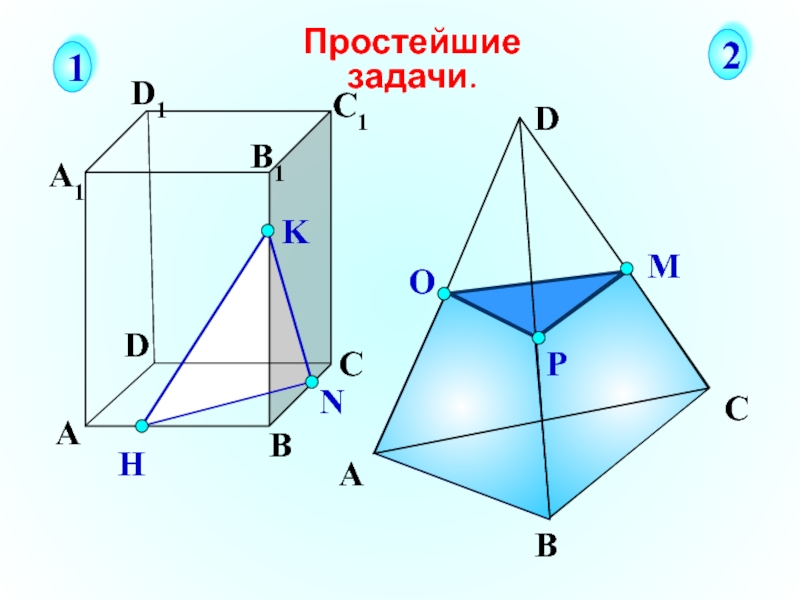
- 11. K
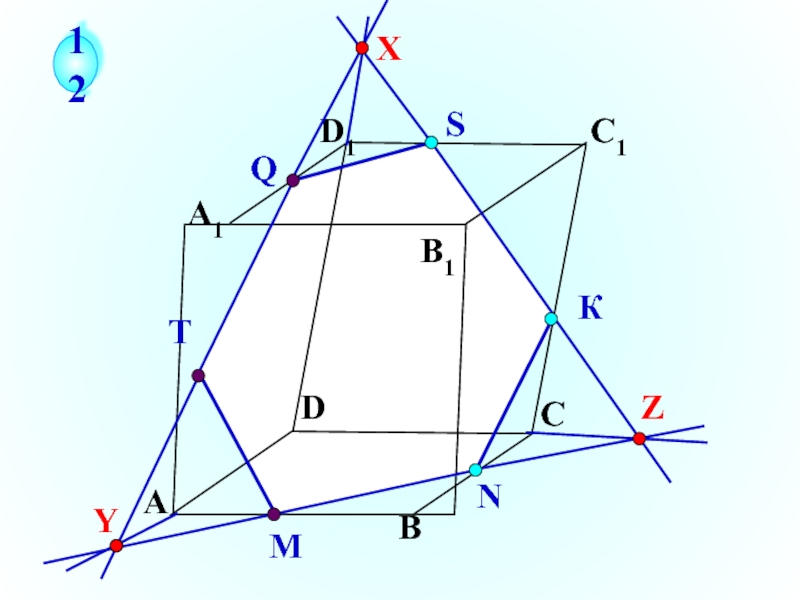
- 12. А В
- 13. Если две
- 14. А В С D
- 17. А В С А1
- 18. K А В С D
- 19. А В С D А1 D1
- 20. А В С D А1
- 21. А В С
- 22. А В С
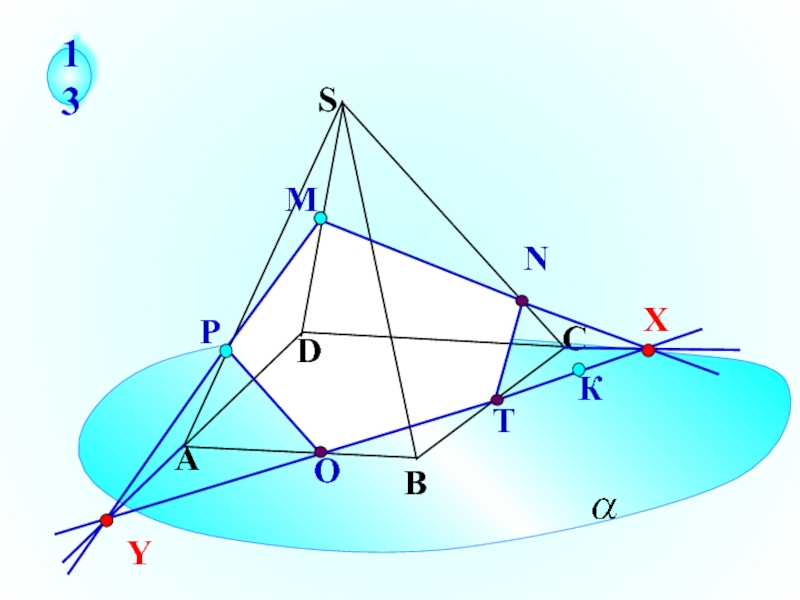
- 23. О М А В С D
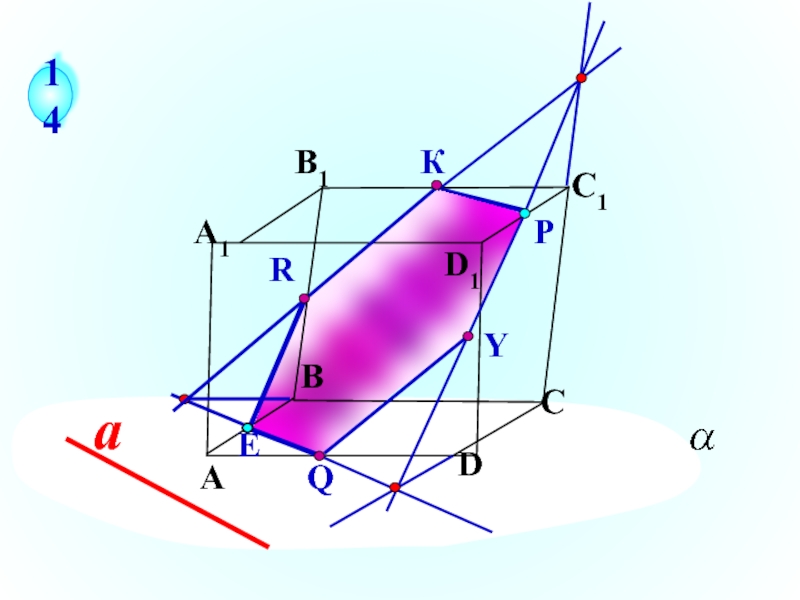
- 24. а
- 25. Многие
- 26. Жос де Мей "Такое может нарисовать
- 27. Законы геометрии часто нарушаются в компьютерных играх.
- 28. K А В С
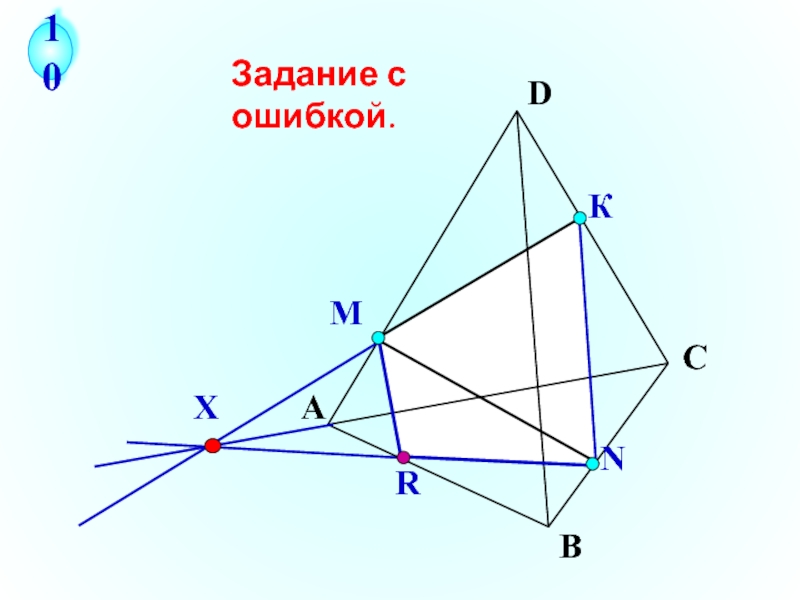
- 29. Задание с ошибкой.
- 30. K
- 31. А В
- 32. Р О
- 33. А D С А1
Слайд 2 Построить сечение многогранника плоскостью – это значит указать точки
Для построения сечения многогранника плоскостью нужно в плоскости каждой грани указать 2 точки, принадлежащие сечению, соединить их прямой и найти точки пересечения этой прямой с ребрами многогранника.
Слайд 13
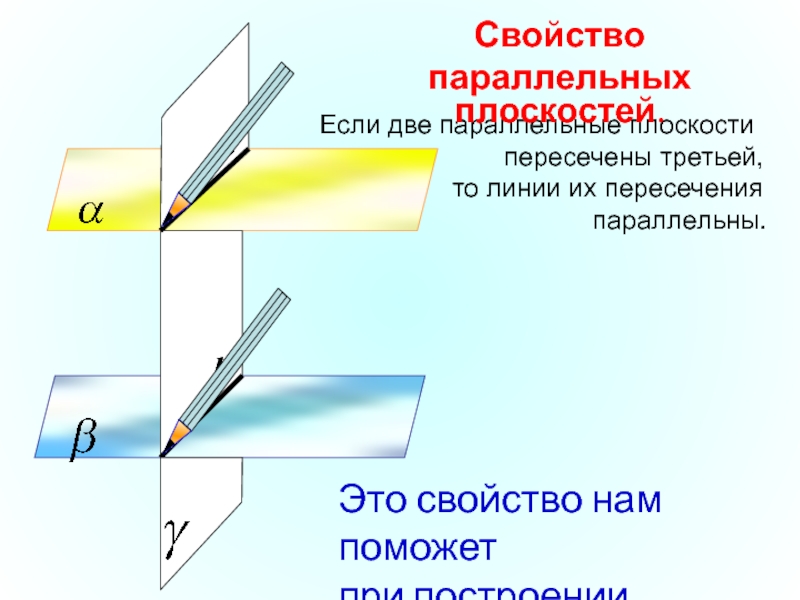
Если две параллельные плоскости
то линии их пересечения
параллельны.
Свойство
параллельных плоскостей.
Это свойство нам поможет
при построении сечений.
Слайд 16
О
9
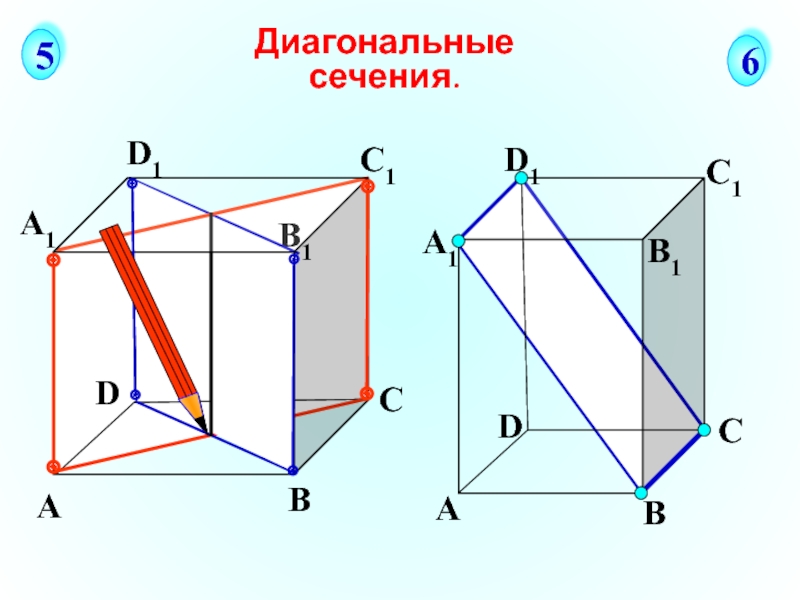
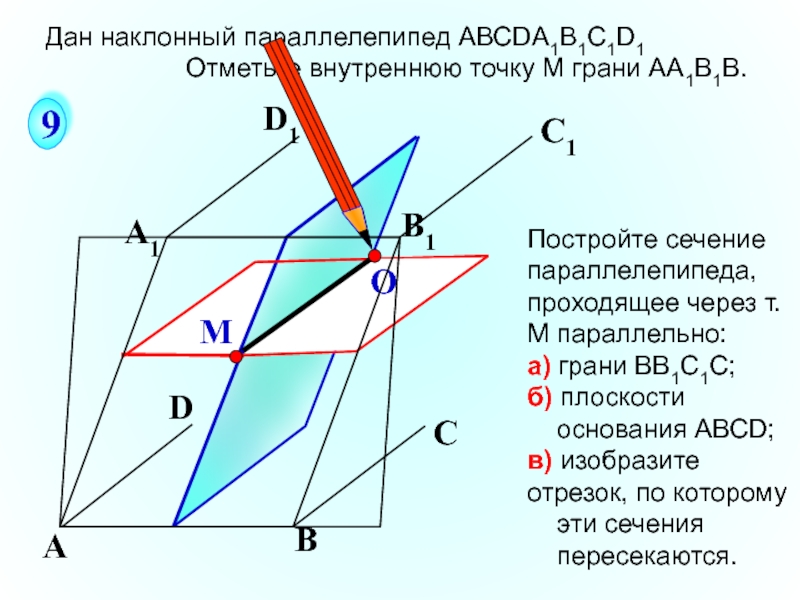
а) грани ВВ1С1С;
б) плоскости
основания АВСD;
в) изобразите
отрезок, по которому
эти сечения
пересекаются.
Дан наклонный параллелепипед АВСDА1В1С1D1
Отметьте внутреннюю точку M грани АА1В1В.
Слайд 17
А
В
С
А1
D1
С1
B1
D
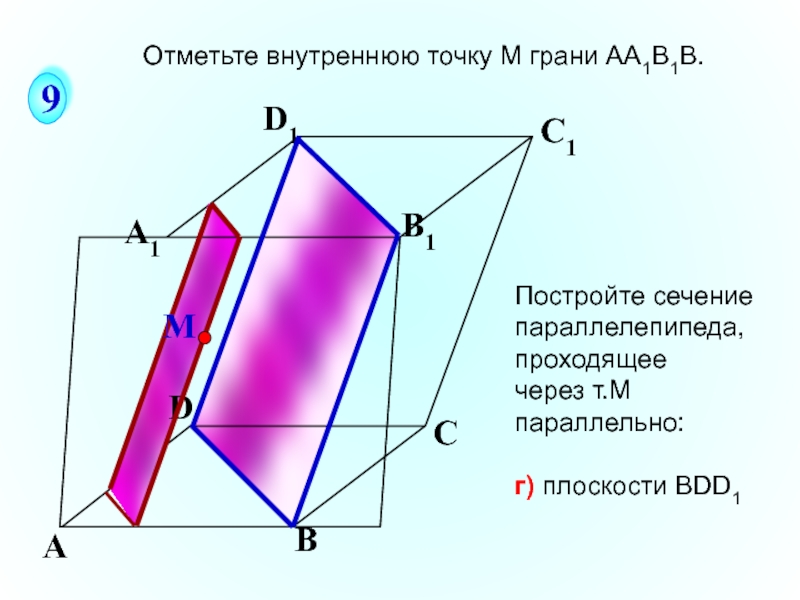
г) плоскости ВDD1
М
9
Отметьте внутреннюю точку M грани АА1В1В.
Слайд 20
А
В
С
D
А1
D1
С1
B1
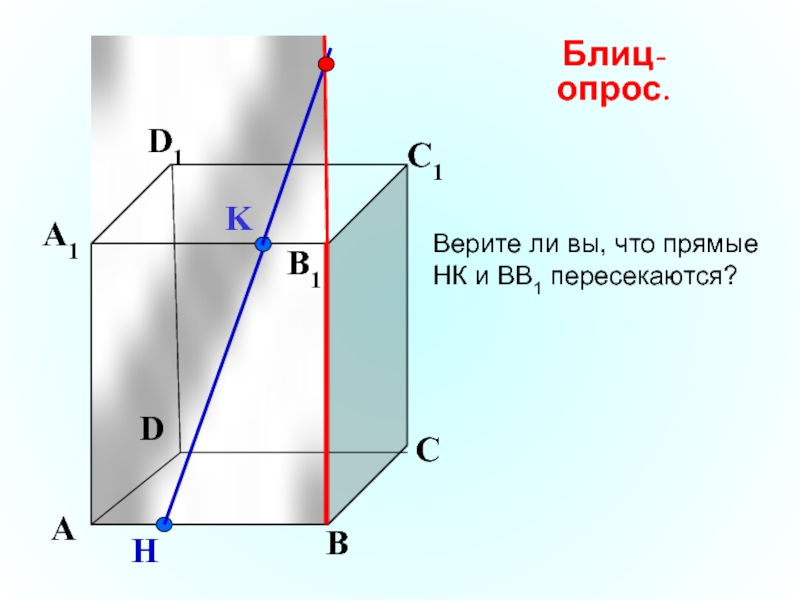
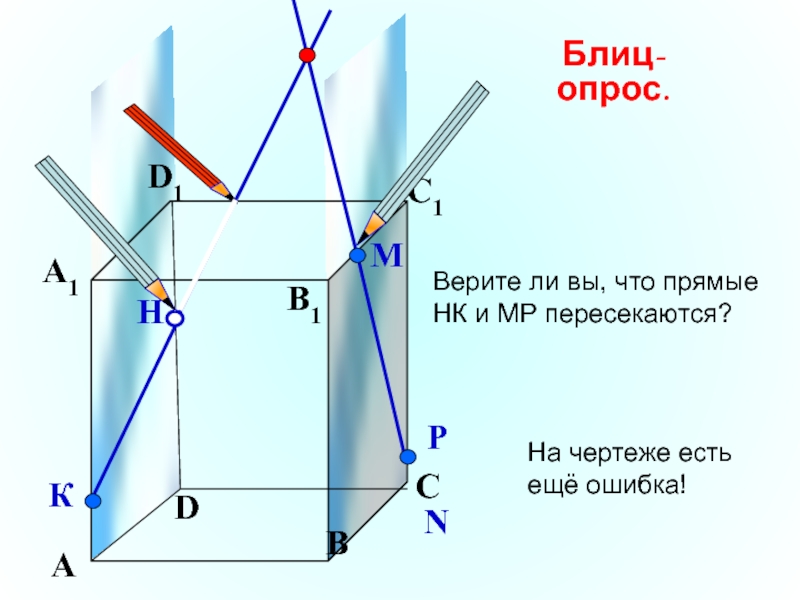
Верите ли вы, что прямые НК и МР пересекаются?
N
Р
Н
К
М
Блиц-опрос.
На чертеже
ещё ошибка!
Слайд 21
А
В
С
D
А1
D1
С1
B1
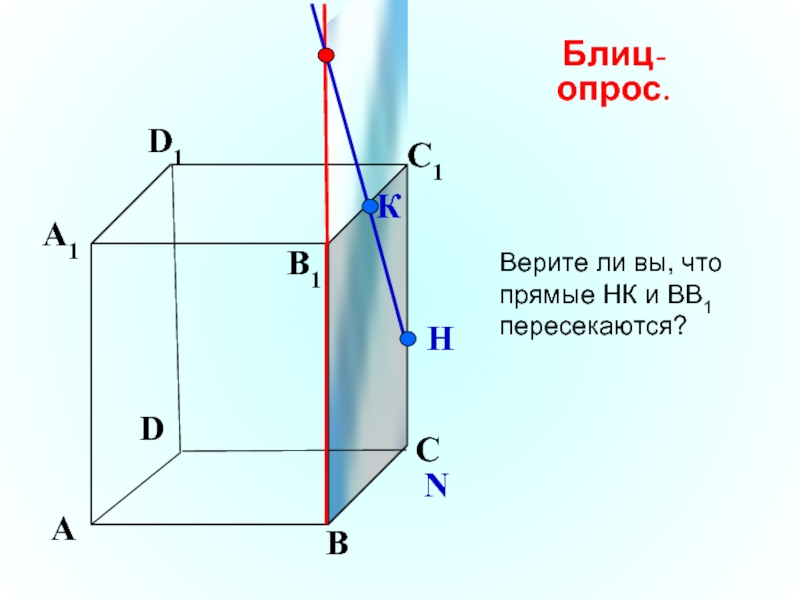
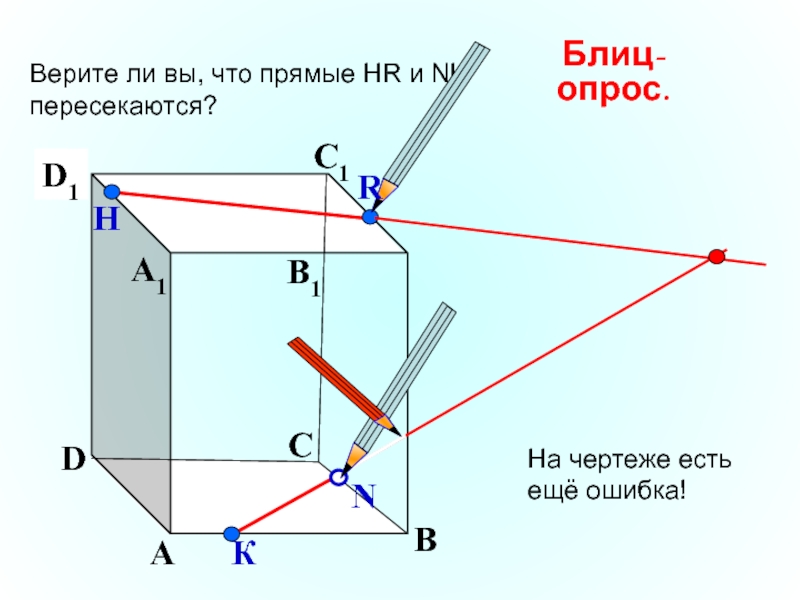
Верите ли вы, что прямые НR и NK
пересекаются?
N
Н
К
Блиц-опрос.
R
На чертеже есть
ещё ошибка!
Слайд 22
А
В
С
D
А1
D1
С1
B1
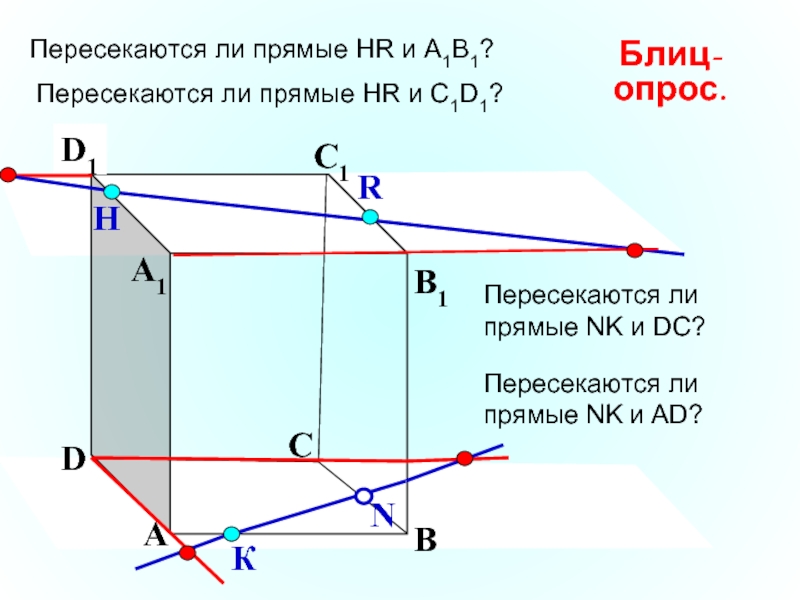
Пересекаются ли прямые НR и А1В1?
N
Н
К
Блиц-опрос.
R
Пересекаются ли прямые НR и
Пересекаются ли
прямые NK и DC?
Пересекаются ли
прямые NK и АD?
Слайд 23
О
М
А
В
С
D
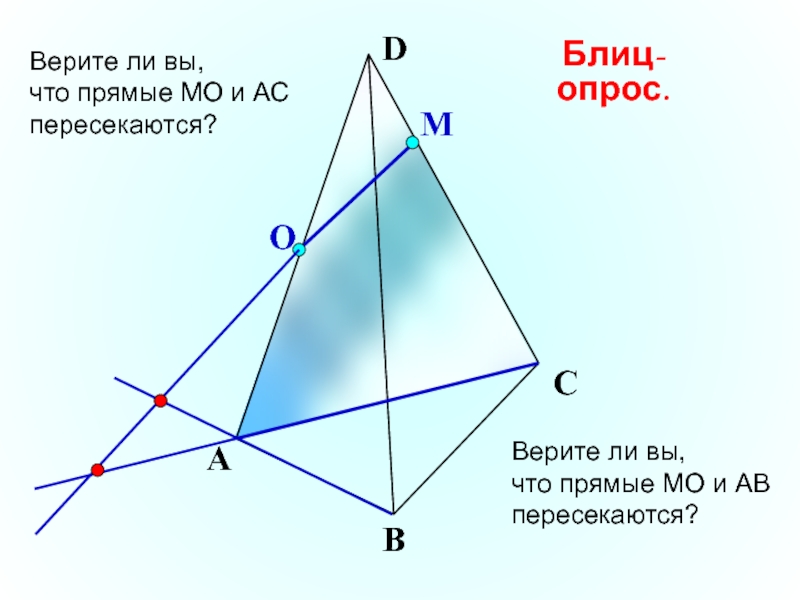
Верите ли вы,
что прямые МО и АС
пересекаются?
Блиц-опрос.
Верите ли вы,
что прямые МО и АВ
пересекаются?
Слайд 24
а
А3. Если две плоскости имеют общую
Некоторые художники любят нарушать эту аксиому.
Слайд 25
Многие художники, искажая законы перспективы, рисуют
Популярные художники Морис Эшер, Оскар Реутерсвард, Жос де Мей и другие, удивляли своими картинами математиков.
http://lib.world-mobile.net/culture/special/imp/imp-world-r.narod.ru/art/index.html
http://www.im-possible.info/english/art/mey/mey2.html
http://alone.sammit.kiev.ua/moremind/illusion/index.html
Это интересно!
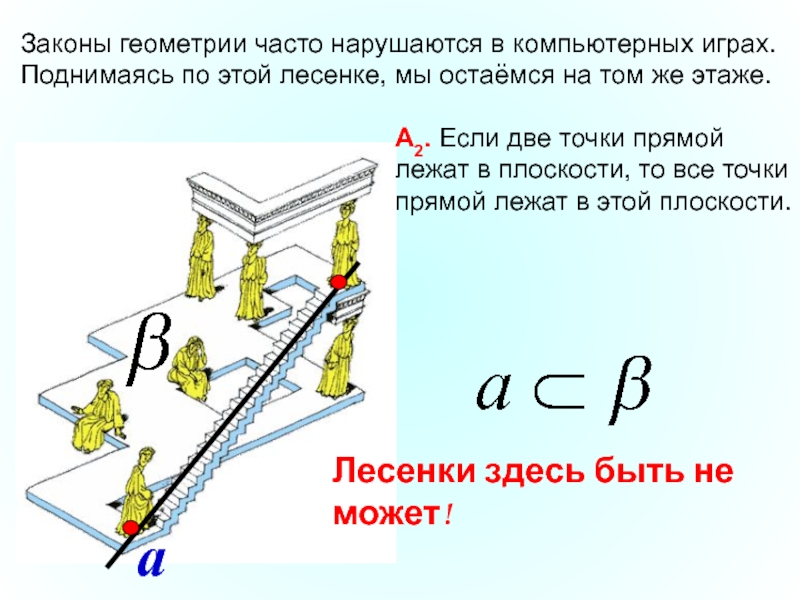
Слайд 27Законы геометрии часто нарушаются в компьютерных играх.
Поднимаясь по этой лесенке, мы
Лесенки здесь быть не может!
а
А2. Если две точки прямой
лежат в плоскости, то все точки
прямой лежат в этой плоскости.