- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое моделирование. (Лекция 3) презентация
Содержание
- 1. Математическое моделирование. (Лекция 3)
- 2. Лекция 3. Математическое моделирование ФГБОУ ВО «УлГПУ
- 3. Лекция 3. Математическое моделирование ФГБОУ ВО «УлГПУ
- 4. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 5. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 6. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 7. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 8. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 9. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 10. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 11. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 12. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 13. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 14. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 15. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 16. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 17. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 18. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 19. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 20. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 21. §1. О моделировании ФГБОУ ВО «УлГПУ им.
- 22. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 23. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 24. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 25. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 26. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 27. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 28. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 29. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 30. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 31. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 32. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 33. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 34. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 35. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 36. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 37. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 38. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 39. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 40. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 41. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 42. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 43. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 44. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 45. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 46. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 47. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 48. §2. Математическое моделирование ФГБОУ ВО «УлГПУ им.
- 49. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 50. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 51. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 52. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 53. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 54. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 55. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 56. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 57. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 58. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 59. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 60. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 61. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 62. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 63. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 64. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 65. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 66. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 67. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 68. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 69. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
- 70. Продолжение следует… Основы математической обработки информации ФГБОУ
Слайд 1Основы математической
обработки информации
Семестр: 1
Лекции: 6
Практические занятия: 10
Контрольная работа: 1
Зачёт
ФГБОУ ВО «УлГПУ
Основы математической обработки информации
лектор Макеева О.В.
Слайд 2Лекция 3. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической
лектор Макеева О.В.
Лекция 3.
Математическое моделирование
§0. «Вопрос науки. Игры разума»
§1. О моделировании
§2. Математическое моделирование
§3. Примеры линейных моделей
§4. Примеры оптимизационных моделей
Слайд 3Лекция 3. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической
лектор Макеева О.В.
«Вопрос науки. Игры разума»
Слайд 4§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Трусов Пётр Валентинович
российский учёный-физик, д.ф.-м.н., специалист в области механики сплошных сред. Автор учебных пособий для студентов ВУЗов по механике сплошных сред, теории определяющих соотношений и математическому моделированию.
Слайд 5§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
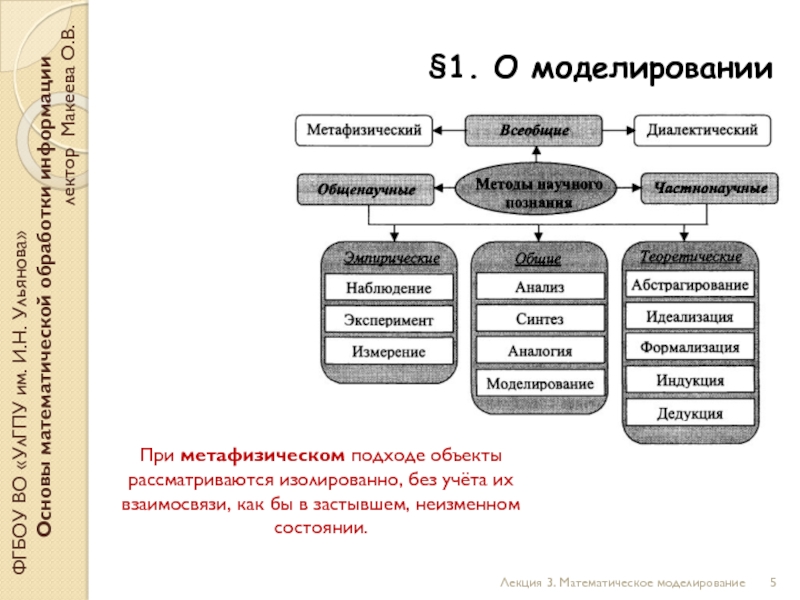
При метафизическом подходе объекты рассматриваются изолированно, без учёта их взаимосвязи, как бы в застывшем, неизменном состоянии.
Слайд 6§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
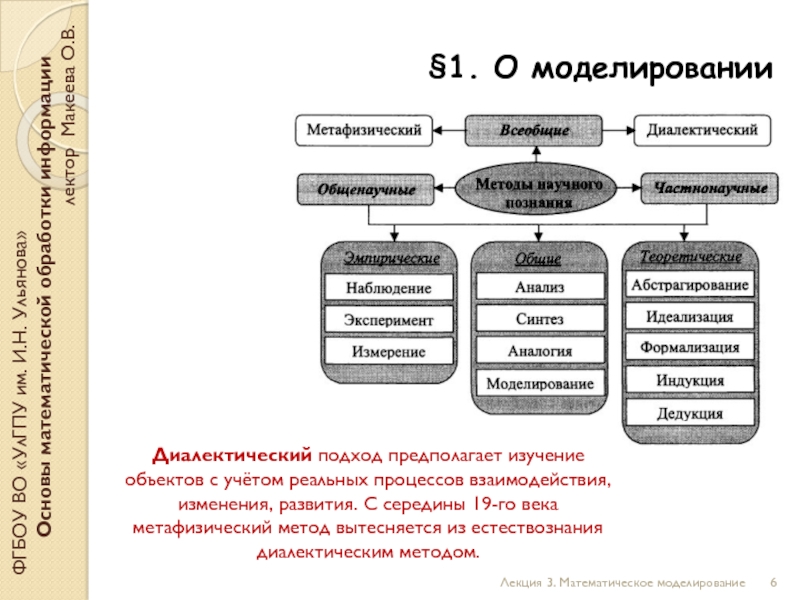
Диалектический подход предполагает изучение объектов с учётом реальных процессов взаимодействия, изменения, развития. С середины 19-го века метафизический метод вытесняется из естествознания диалектическим методом.
Слайд 7§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
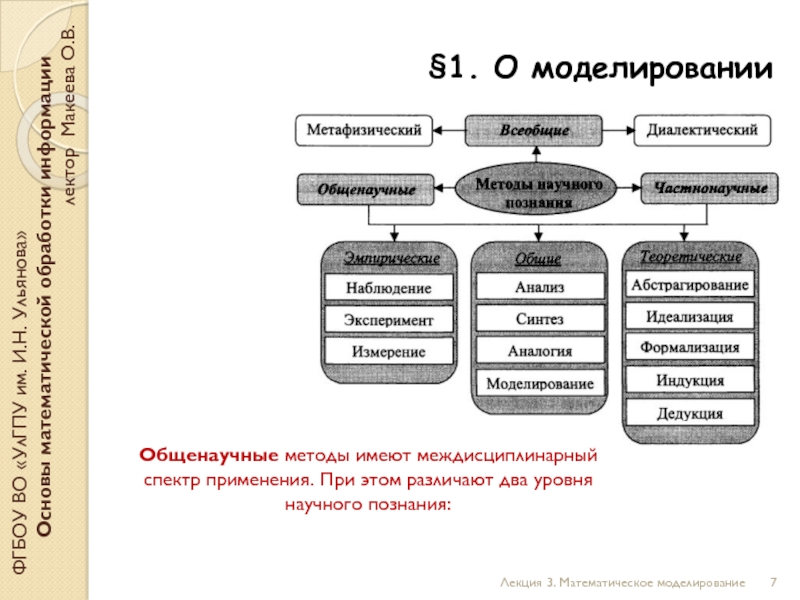
Общенаучные методы имеют междисциплинарный спектр применения. При этом различают два уровня научного познания:
Слайд 8§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
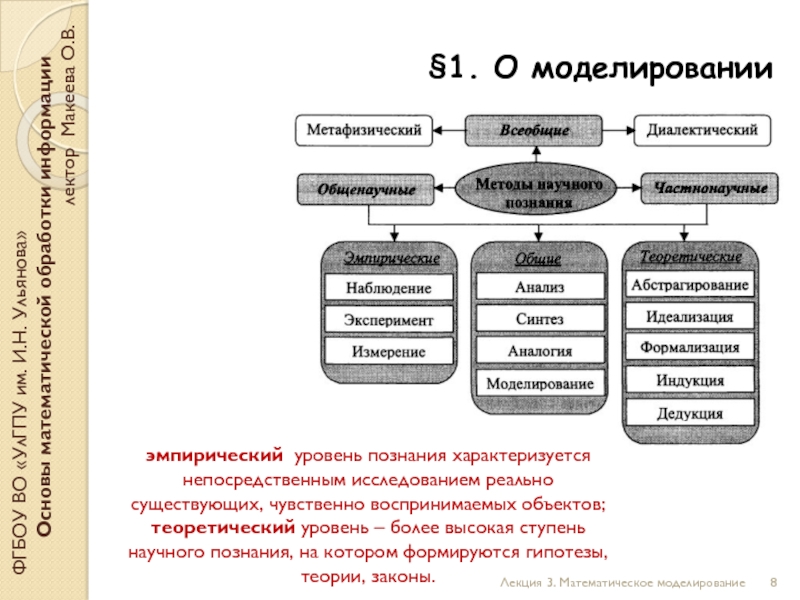
эмпирический уровень познания характеризуется непосредственным исследованием реально существующих, чувственно воспринимаемых объектов;
теоретический уровень – более высокая ступень научного познания, на котором формируются гипотезы, теории, законы.
Слайд 9§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Частнонаучные методы используются лишь в рамках какой-либо конкретной науки.
Слайд 10§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Моделирование – метод познания окружающего мира, который можно отнести к общенаучным методам, применяемым как на эмпирическом, так и теоретическом уровне познания.
Модель (от лат. modulus – мера, образец, норма) – материальный или мысленно представляемый объект, который в процессе изучения замещает объект – оригинал, сохраняя некоторые важные для данного исследования типичные черты.
Процесс построения и использования модели называется моделированием.
Слайд 11§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Виды моделирования
Слайд 12§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
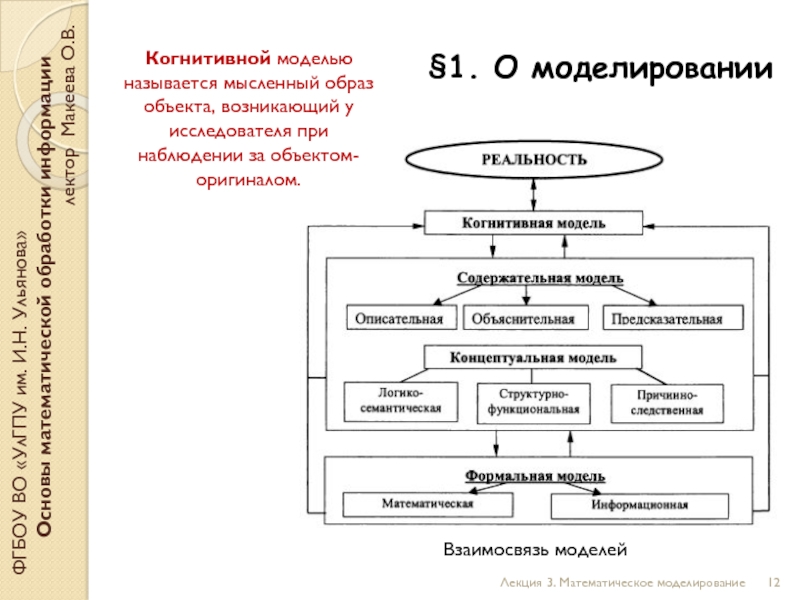
Взаимосвязь моделей
Когнитивной моделью называется мысленный образ объекта, возникающий у исследователя при наблюдении за объектом-оригиналом.
Слайд 13§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Взаимосвязь моделей
Представление модели на естественном языке называется содержательной моделью.
Слайд 14§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Взаимосвязь моделей
По функциональному признаку модели делят на описательные, объяснительные и прогностические.
Слайд 15§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
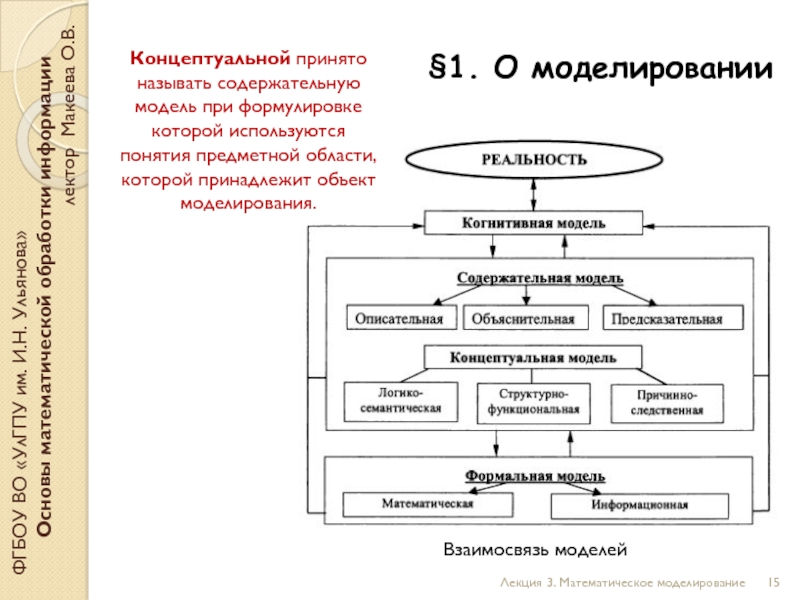
Взаимосвязь моделей
Концептуальной принято называть содержательную модель при формулировке которой используются понятия предметной области, которой принадлежит объект моделирования.
Слайд 16§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Взаимосвязь моделей
Логика семантическая модель использует при описании логически непротиворечивые утверждения и факты.
Слайд 17§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
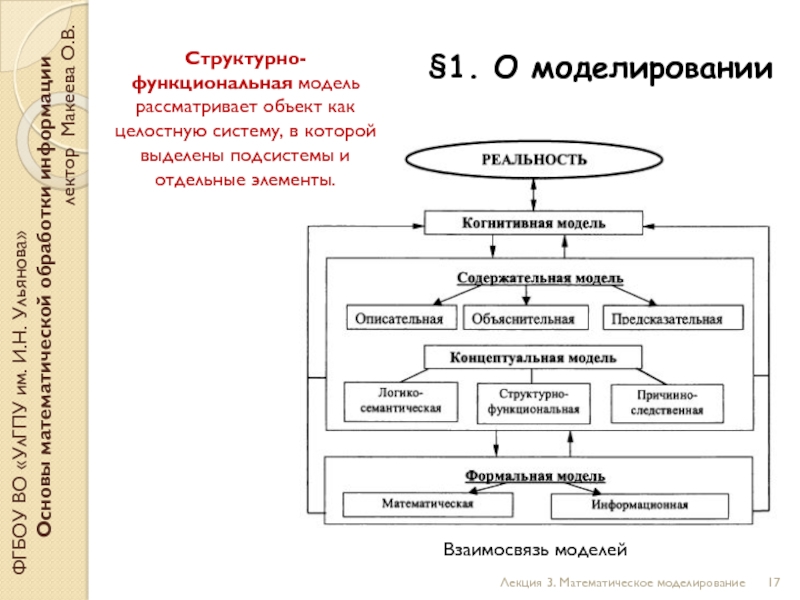
Взаимосвязь моделей
Структурно-функциональная модель рассматривает объект как целостную систему, в которой выделены подсистемы и отдельные элементы.
Слайд 18§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
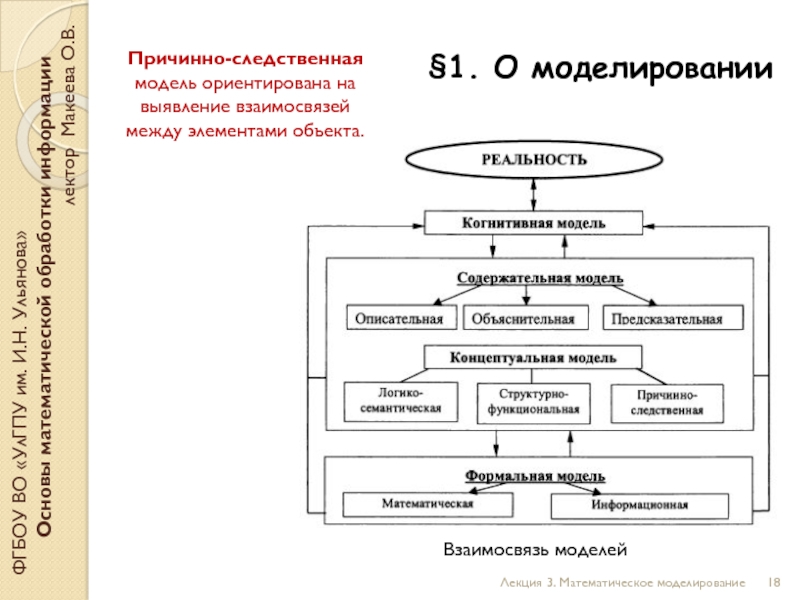
Взаимосвязь моделей
Причинно-следственная модель ориентирована на выявление взаимосвязей между элементами объекта.
Слайд 19§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Взаимосвязь моделей
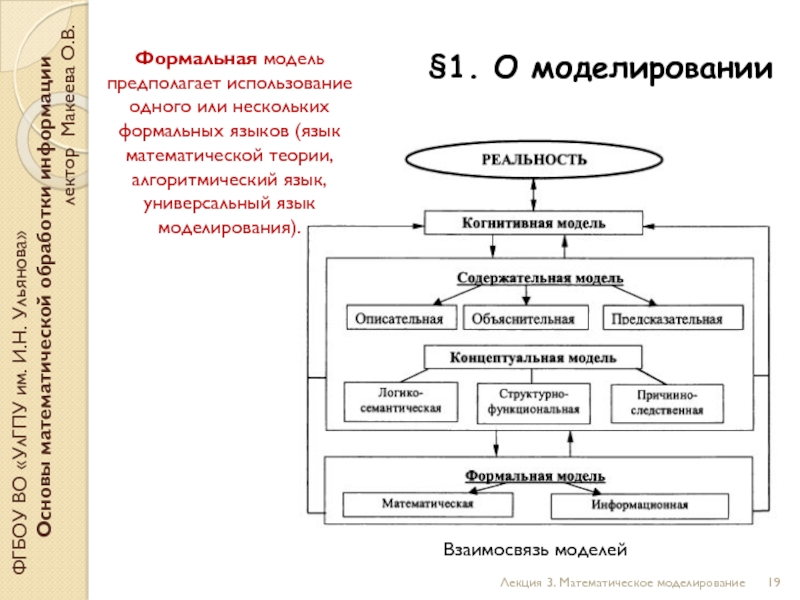
Формальная модель предполагает использование одного или нескольких формальных языков (язык математической теории, алгоритмический язык, универсальный язык моделирования).
Слайд 20§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Взаимосвязь моделей
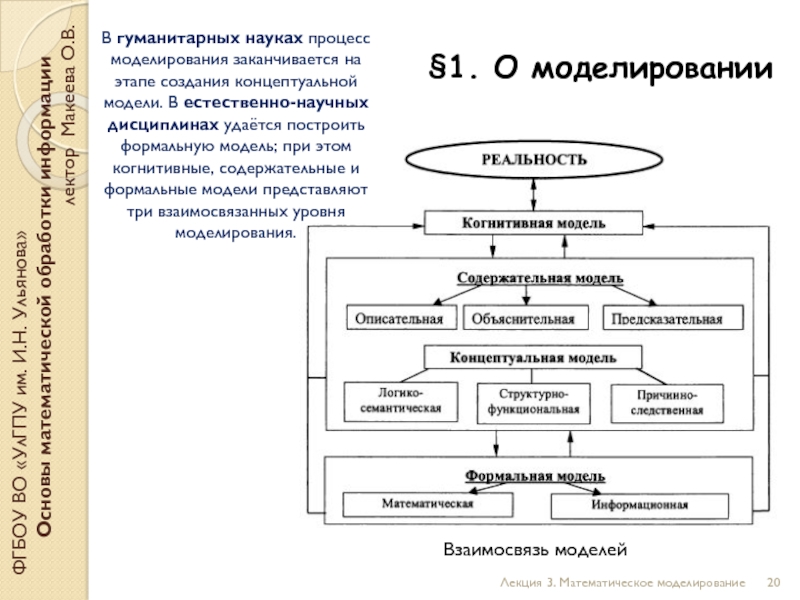
В гуманитарных науках процесс моделирования заканчивается на этапе создания концептуальной модели. В естественно-научных дисциплинах удаётся построить формальную модель; при этом когнитивные, содержательные и формальные модели представляют три взаимосвязанных уровня моделирования.
Слайд 21§1. О моделировании
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Взаимосвязь моделей
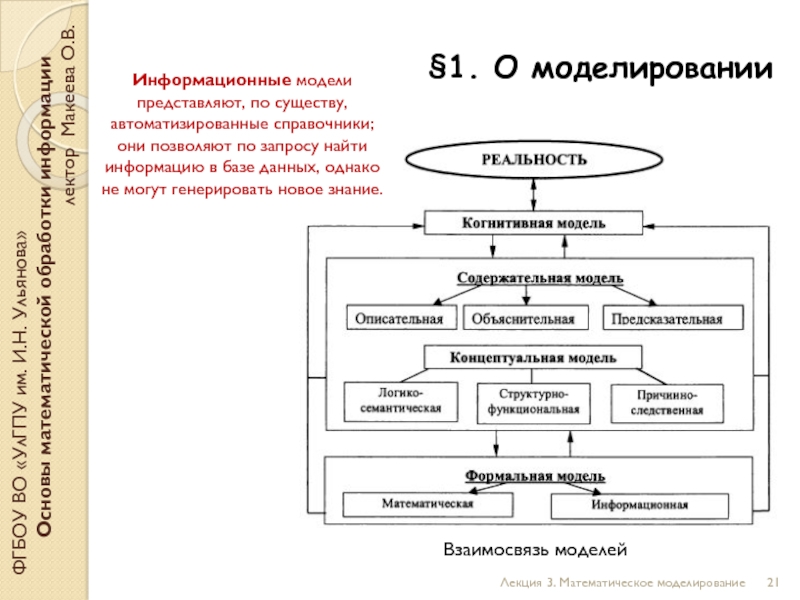
Информационные модели представляют, по существу, автоматизированные справочники; они позволяют по запросу найти информацию в базе данных, однако не могут генерировать новое знание.
Слайд 22§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Виды моделирования
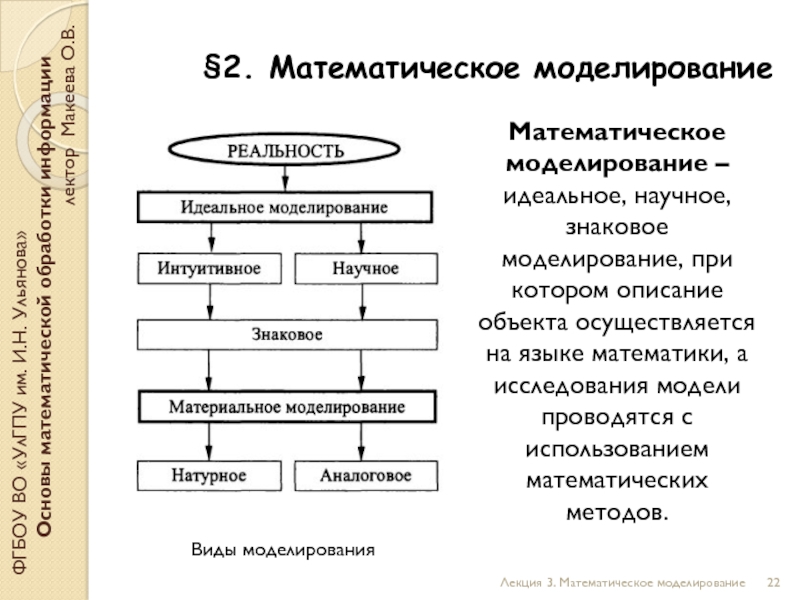
Математическое моделирование – идеальное, научное, знаковое моделирование, при котором описание объекта осуществляется на языке математики, а исследования модели проводятся с использованием математических методов.
Слайд 23§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
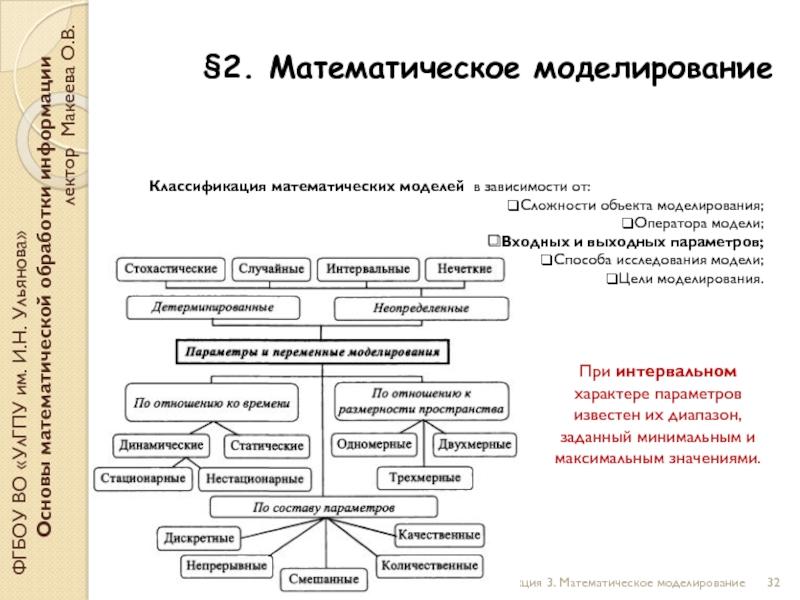
Классификация математических моделей
в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
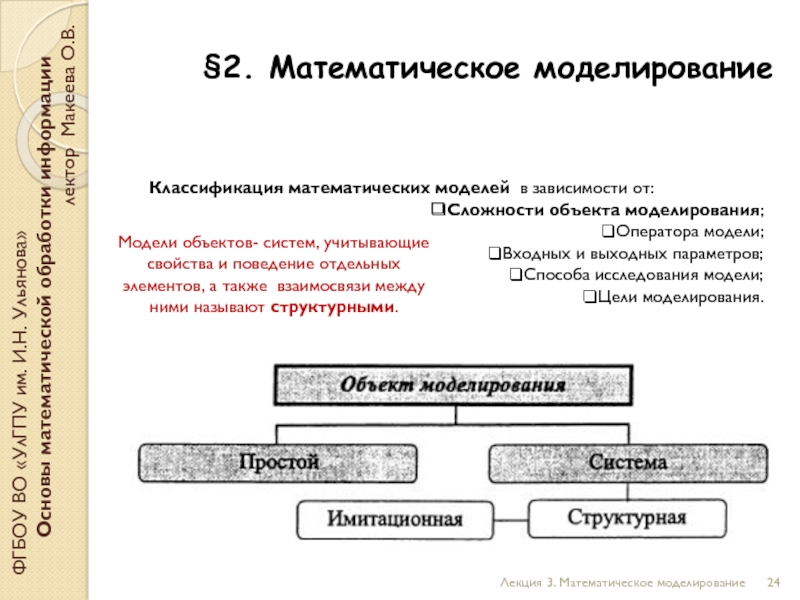
Слайд 24§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Модели объектов- систем, учитывающие свойства и поведение отдельных элементов, а также взаимосвязи между ними называют структурными.
Слайд 25§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Структурную модель называют имитационной, если каждый элемент имеет конечное число состояний.
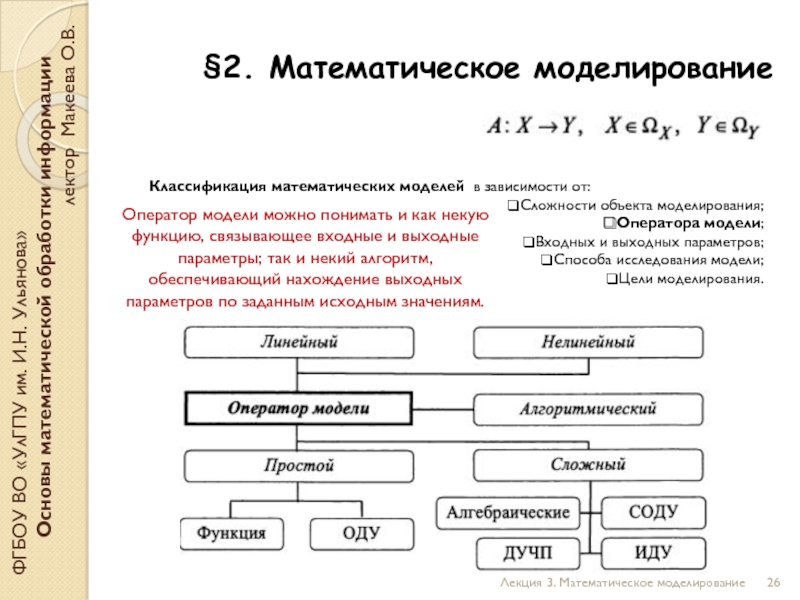
Слайд 26§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Оператор модели можно понимать и как некую функцию, связывающее входные и выходные параметры; так и некий алгоритм, обеспечивающий нахождение выходных параметров по заданным исходным значениям.
Слайд 27§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
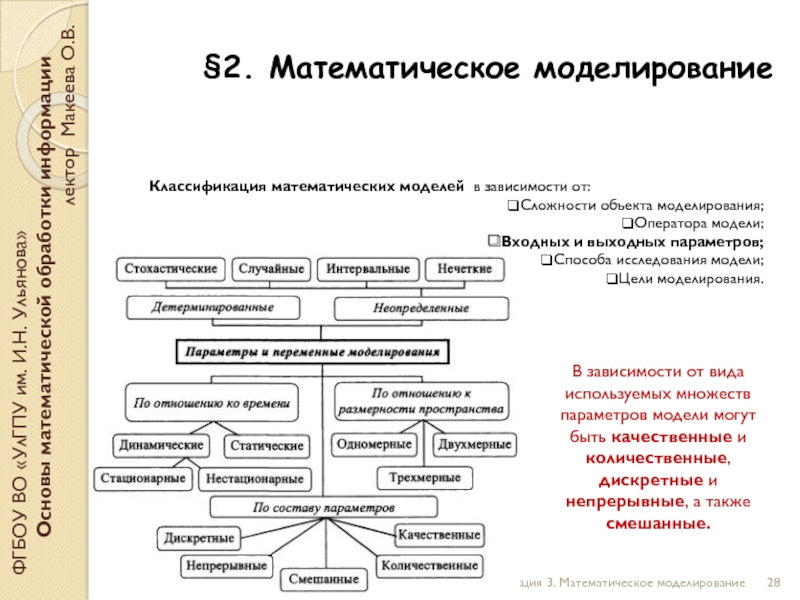
Слайд 28§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
В зависимости от вида используемых множеств параметров модели могут быть качественные и количественные, дискретные и непрерывные, а также смешанные.
Слайд 29§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Детерминированные модели характеризуются определённостью всех параметров.
Слайд 30§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
В стохастических моделях значения всех или некоторых параметров определяются случайными величинами, заданными плотностями вероятности.
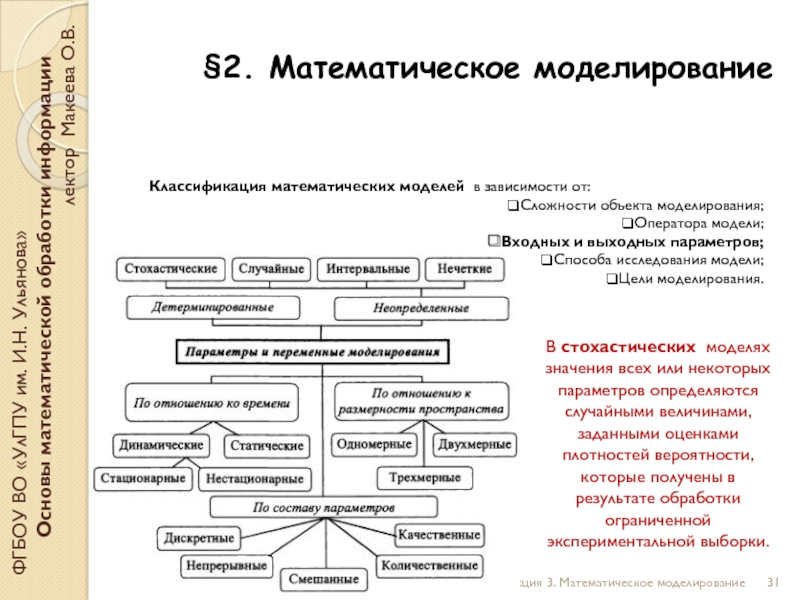
Слайд 31§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
В стохастических моделях значения всех или некоторых параметров определяются случайными величинами, заданными оценками плотностей вероятности, которые получены в результате обработки ограниченной экспериментальной выборки.
Слайд 32§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
При интервальном характере параметров известен их диапазон, заданный минимальным и максимальным значениями.
Слайд 33§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
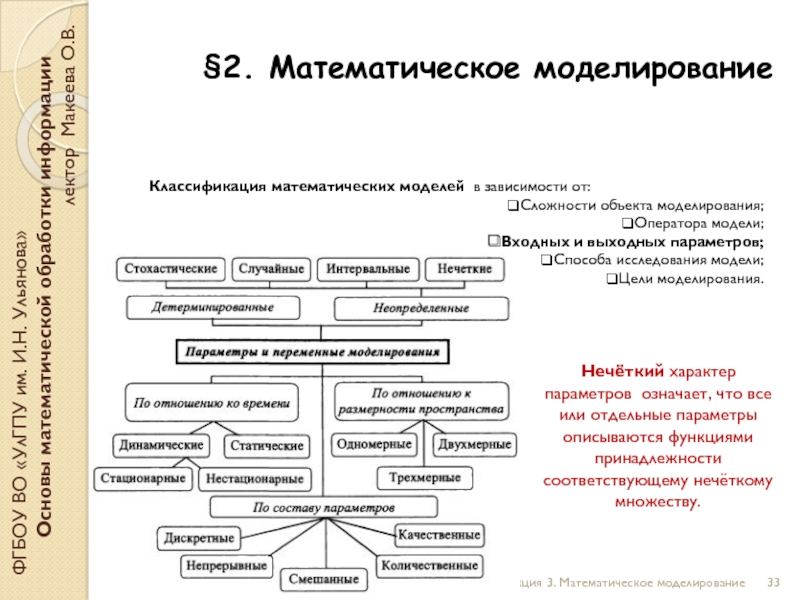
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Нечёткий характер параметров означает, что все или отдельные параметры описываются функциями принадлежности соответствующему нечёткому множеству.
Слайд 34§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Модели среди параметров которых есть координаты пространства делят на одномерные, двумерные и трёхмерные.
Слайд 35§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Если при исследовании объекта необходим учёт времени, то модель называют динамической.
Слайд 36§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
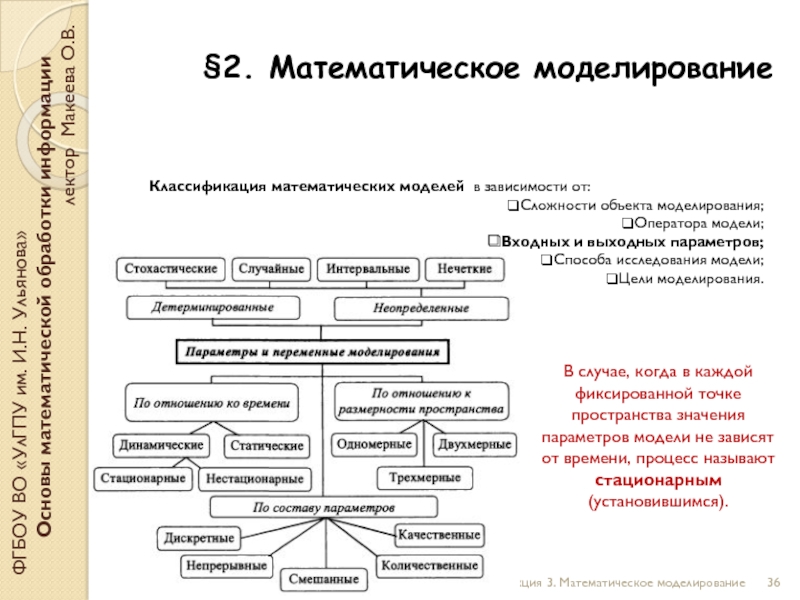
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
В случае, когда в каждой фиксированной точке пространства значения параметров модели не зависят от времени, процесс называют стационарным (установившимся).
Слайд 37§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
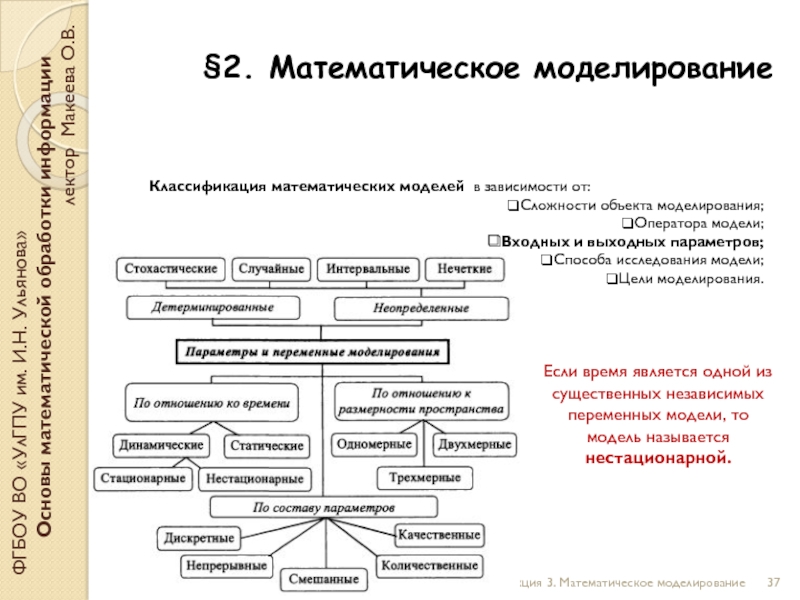
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Если время является одной из существенных независимых переменных модели, то модель называется нестационарной.
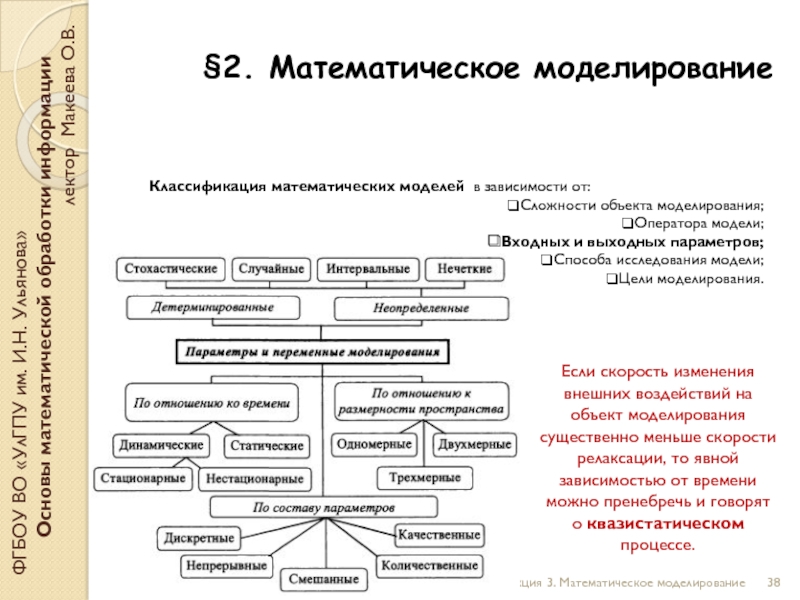
Слайд 38§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Если скорость изменения внешних воздействий на объект моделирования существенно меньше скорости релаксации, то явной зависимостью от времени можно пренебречь и говорят о квазистатическом процессе.
Слайд 39§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
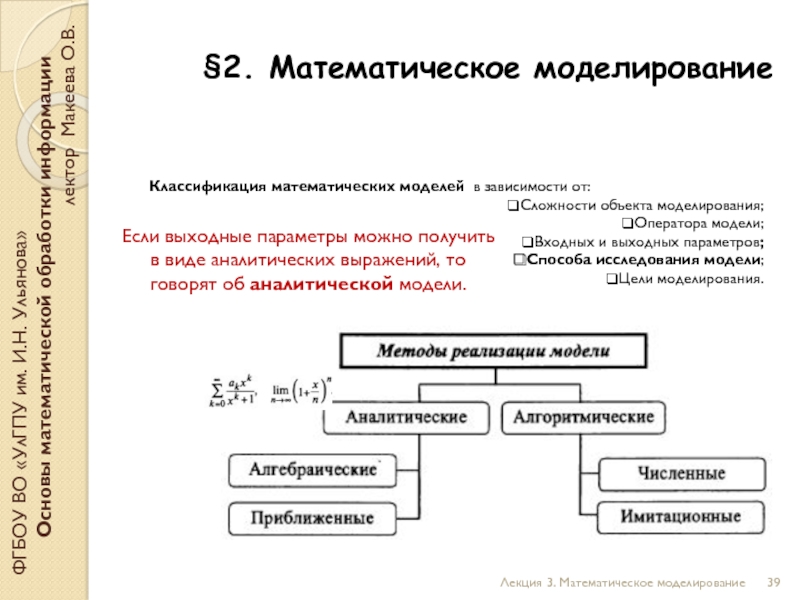
Если выходные параметры можно получить в виде аналитических выражений, то говорят об аналитической модели.
Слайд 40§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
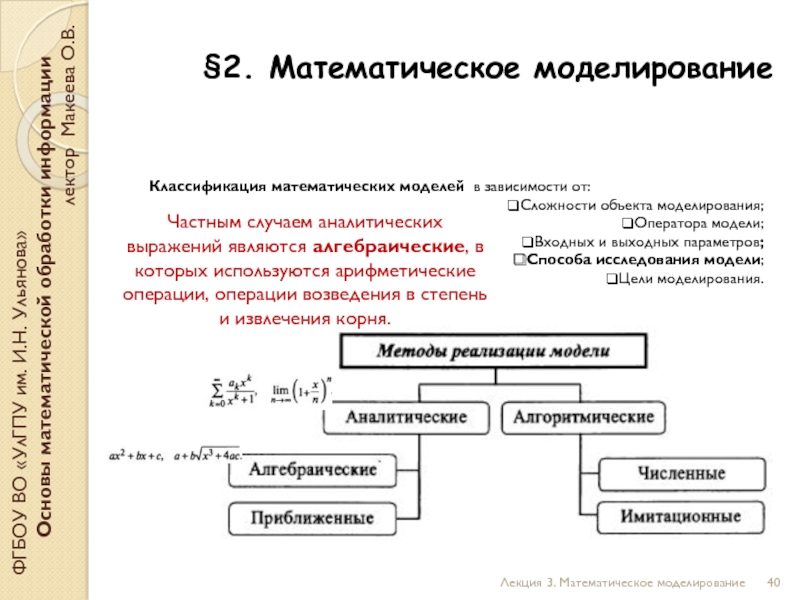
Частным случаем аналитических выражений являются алгебраические, в которых используются арифметические операции, операции возведения в степень и извлечения корня.
Слайд 41§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
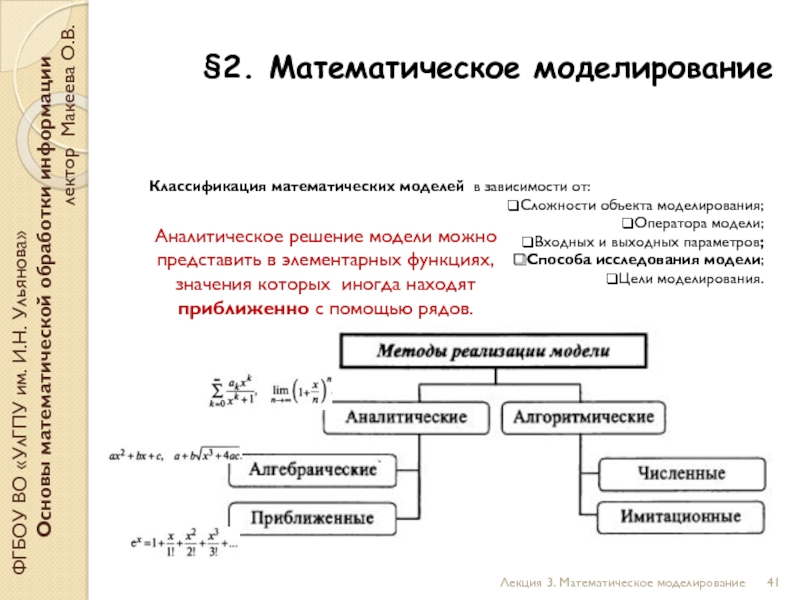
Аналитическое решение модели можно представить в элементарных функциях, значения которых иногда находят приближенно с помощью рядов.
Слайд 42§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
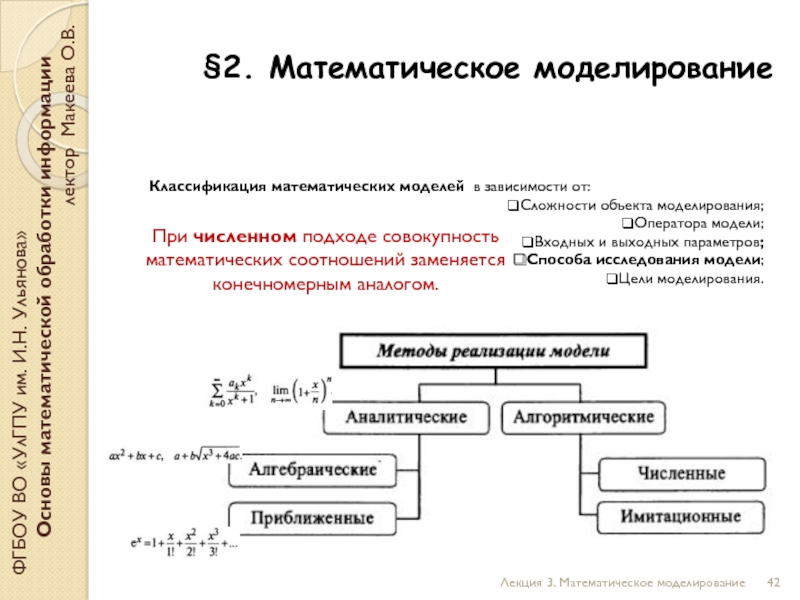
При численном подходе совокупность математических соотношений заменяется конечномерным аналогом.
Слайд 43§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
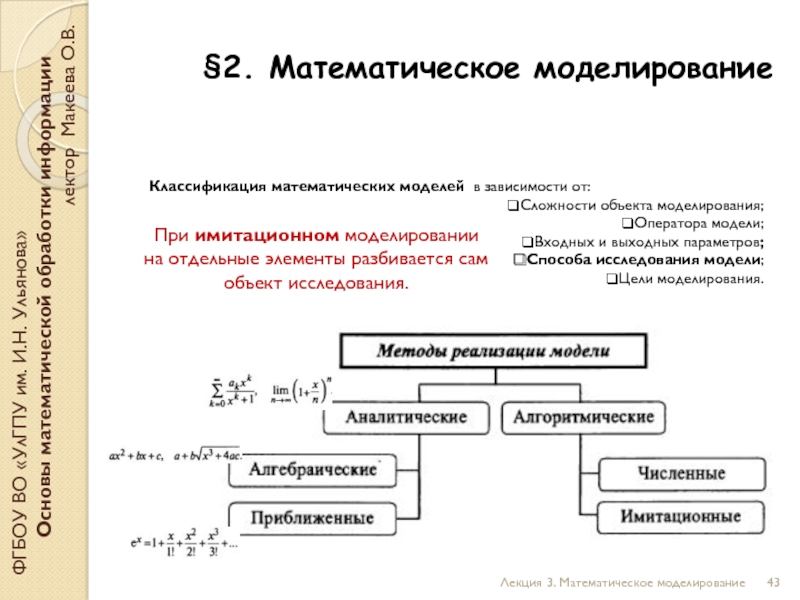
При имитационном моделировании
на отдельные элементы разбивается сам объект исследования.
Слайд 44§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Слайд 45§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
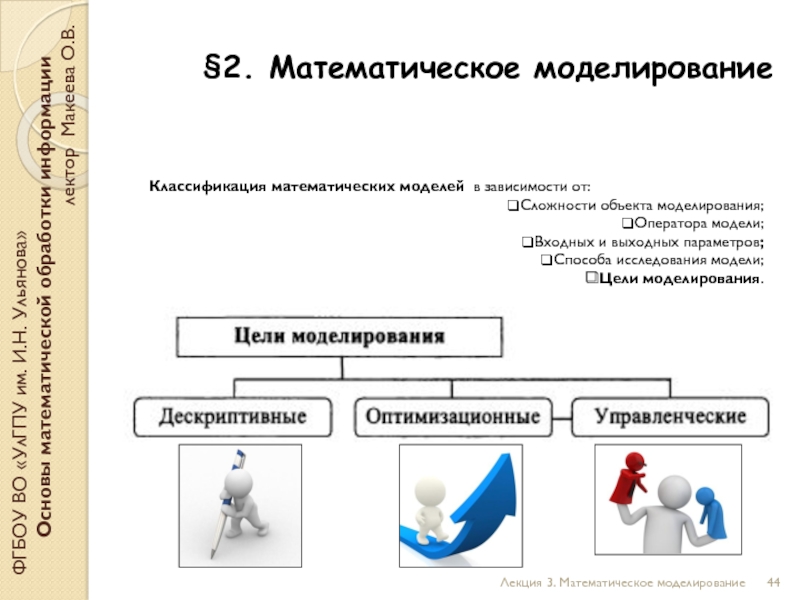
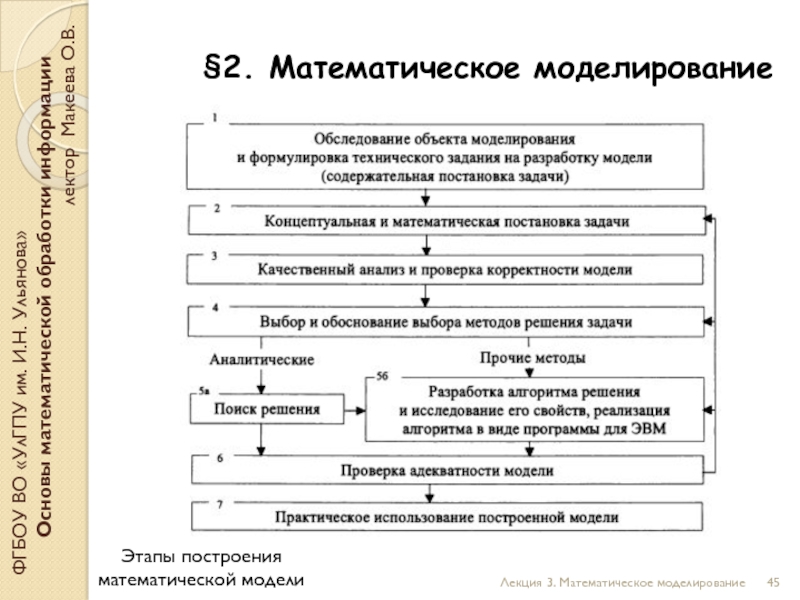
Этапы построения математической модели
Слайд 46§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Этапы построения математической модели
Слайд 47§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Этапы построения математической модели
Слайд 48§2. Математическое моделирование
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки
лектор Макеева О.В.
Лекция 3. Математическое моделирование
Этапы построения математической модели
Слайд 49ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
Этапы построения математической модели
§2. Математическое моделирование
Слайд 50ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
Этапы построения математической модели
§2. Математическое моделирование
Слайд 51ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
Этапы построения математической модели
§2. Математическое моделирование
Слайд 52ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
Этапы построения математической модели
§2. Математическое моделирование
Слайд 53ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
Этапы построения математической модели
§2. Математическое моделирование
Слайд 54ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
Этапы построения математической модели
§2. Математическое моделирование
Слайд 55ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
Этапы построения математической модели
§2. Математическое моделирование
Слайд 56ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
Этапы построения математической модели
§2. Математическое моделирование
Слайд 57ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
Этапы построения математической модели
§2. Математическое моделирование
Слайд 58ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
Этапы построения математической модели
§2. Математическое моделирование
Слайд 59ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
§3. Примеры линейных моделей
Абатурова Вера Сергеевна
к.п.н.; зав. отделом образовательных и информационных технологий Южного математического института Владикавказского научного центра РАН;
директор ВЦНМО
Слайд 60ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
§3. Примеры линейных моделей
Система уравнений
а - количество единиц травы, которое было на лугу первоначально;
b - количество единиц травы, которое ежедневно вырастает на лугу;
с - количество единиц травы, которое ежедневно съедает одна корова.
Ответ: 20 коров.
Слайд 61ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
§3. Примеры линейных моделей
Система уравнений
а - количество единиц травы, которое было на лугу первоначально;
b - количество единиц травы, которое ежедневно вырастает на лугу;
с - количество единиц травы, которое ежедневно съедает одна корова.
Ответ: 20 коров.
1. Выбор переменных.
2. Запись ограничений на переменные.
3. Формулировка требований задачи на языке математики (с помощью переменных).
4. Решение математической задачи.
5. Интерпретация результатов. Запись ответа.
Слайд 62ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
§3. Примеры линейных моделей
Система неравенств
х – вес купленных слив (кг);
у – вес купленных яблок (кг).
Слайд 63ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
§3. Примеры линейных моделей
Система неравенств
х – вес купленных слив (кг);
у – вес купленных яблок (кг).
Слайд 64ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
§4. Примеры оптимизационных моделей
Линейное программирование
Слайд 65ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
§4. Примеры оптимизационных моделей
Линейное программирование
х1 – вес картофеля, который покупается у поставщика А (т);
х2 – вес картофеля, который покупается у поставщика В (т).
Слайд 66ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
§4. Примеры оптимизационных моделей
Линейное программирование
Слайд 67ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
§4. Примеры оптимизационных моделей
Линейное программирование
Слайд 68ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
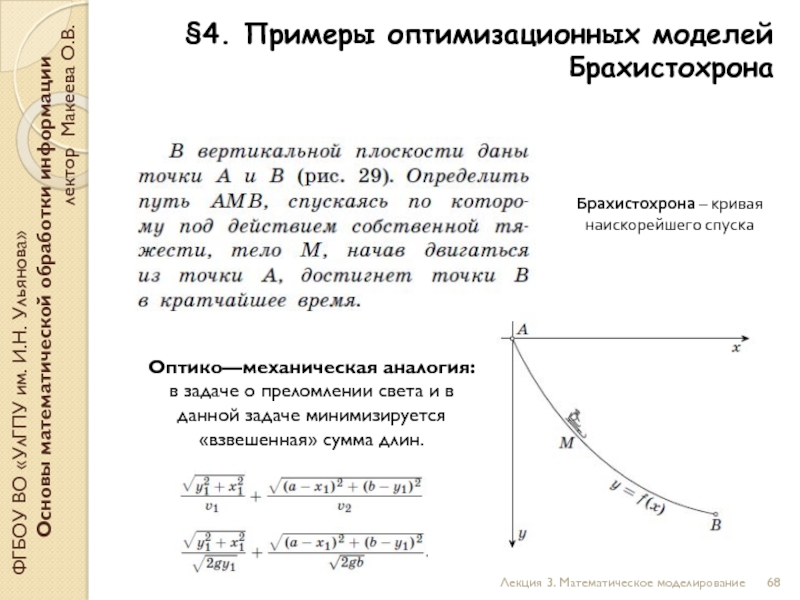
§4. Примеры оптимизационных моделей
Брахистохрона
Оптико—механическая аналогия:
в задаче о преломлении света и в данной задаче минимизируется «взвешенная» сумма длин.
Брахистохрона – кривая наискорейшего спуска
Слайд 69ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева
Лекция 3. Математическое моделирование
§4. Примеры оптимизационных моделей
Циклоида
Слайд 70Продолжение следует…
Основы математической
обработки информации
ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической
лектор Макеева О.В.