- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое дополнение презентация
Содержание
- 1. Математическое дополнение
- 2. б) вычитание векторов в) скалярное произведение двух векторов
- 3. г) векторное произведение двух векторов д)
- 4. 2. Выражение вектора через его проекции на
- 5. Координатная запись скалярного и векторного произведений: Смешанное
- 6. 3. Предел. Если переменная величина (скорость, ускорение,
- 7. Формулы дифференциального исчисления
- 8. Производная функции
- 9. Пример:
- 10. Для функции многих переменных
- 11. 5. Интеграл. 5.1 Определенный интеграл Сумму
- 12. Основные свойства определенного интеграла.
- 13. Среднее значение функции f(x) в интервале
- 14. 5.2 Неопределенный интеграл Если в задаче необходимо
- 15. Формулы интегрального исчисления
- 16. Десятичные приставки к названиям единиц и их наименования
- 17. Некоторые тригонометрические формулы
- 18. Формулы для приближенных вычислений Если
Слайд 1Математическое дополнение
Скаляры и векторы
Скалярная величина полностью определяется модулем и знаком.
Примеры
Векторная величина характеризуется модулем и направлением.
Примеры векторных величин: скорость, перемещение, сила.
Правила векторного исчисления:
а) сложение векторов ( по правилу параллелограмма или треугольника)
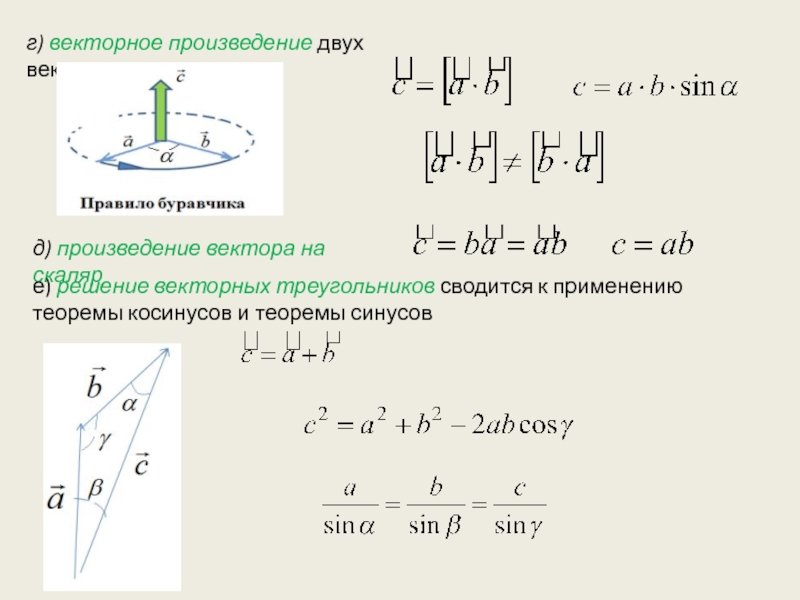
Слайд 3г) векторное произведение двух векторов
д) произведение вектора на скаляр
е)
Слайд 42. Выражение вектора через его проекции на координатные оси.
,
Проекции векторной суммы на оси координат:
или
Слайд 5Координатная запись скалярного и векторного произведений:
Смешанное произведение:
Двойное векторное произведение:
Можно запомнить так:
Слайд 63. Предел.
Если переменная величина (скорость, ускорение, сила) в рассматриваемом случае неограниченно
4. Производная и дифференциал
Производная функции
- дифференциал функции, - дифференциал аргумента.
Слайд 8Производная функции или вторая
Применение производных для исследования функций.
В точках экстремума функции ее производная обращается в ноль:
В точках максимума функции ее вторая производная отрицательна:
В точках минимума функции ее вторая производная положительна:
Слайд 10Для функции многих переменных
где - частные производные функции. Это производные по
одному из аргументов, вычисленные в предположении, что остальные аргументы постоянны.
Слайд 115. Интеграл.
5.1 Определенный интеграл
Сумму
что на каждом из этих интервалов ,
обозначают и называют
определенным интегралом от в интервале .
Графически этот интеграл представляет площадь фигуры под кривой .
Пример: работа силы при конечном перемещении вдоль OX :
Слайд 13Среднее значение функции f(x) в интервале
Пример: . На интервале :
a
f
x
0
Среднее значение линейной функции на интервале равно полусумме ее значений на концах интервала.
Слайд 145.2 Неопределенный интеграл
Если в задаче необходимо узнать не численный ответ:
а саму
Здесь С – произвольная постоянная, определяемая при решении конкретной задачи.
Пример:
Слайд 18Формулы для приближенных вычислений
Если
Если угол α мал и выражен в радианах, то в первом приближении можно принять: