Аналитическая статистика.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теоретические распределения в анализе вариационных рядов презентация
Содержание
- 1. Теоретические распределения в анализе вариационных рядов
- 2. 2 Общие сведения о математическом моделировании Различают
- 3. 3 Моделирование рядов распределения Если имеется эмпирический
- 4. 4 Моделирование рядов распределения Основные свойства кривой
- 5. 5 Моделирование рядов распределения Связь между
- 6. 6 Расчет теоретических частот нормального распределения Пример.
- 7. 7 Расчет теоретических частот нормального распределения
- 8. 8 Расчет теоретических частот нормального распределения
- 9. 9 Методы расчета значений теоретической нормированной функции
- 10. 10 Методы расчета значений теоретической нормированной функции
- 11. 11 Критерий согласия Пирсона Критерий согласия
- 12. 12 Критерий согласия Пирсона Способы нахождения
- 13. 13 Критерий согласия Пирсона 2. С помощью стандартной функции Excel ХИ2ТЕСТ.
- 14. 14 Критерий согласия Пирсона Рассчитав значение
- 15. 15 Критерий согласия Колмогорова Критерий согласия
- 16. 16 Критерий согласия Романовского Критерий согласия
Слайд 1Автор: Равичев Л.В.
РХТУ им. Д.И.Менделеева
Кафедра управления технологическими инновациями
Москва - 2013
СТАТИСТИКА.
Лекция
Слайд 22
Общие сведения о математическом моделировании
Различают два вида зависимостей между явлениями и
Слайд 33
Моделирование рядов распределения
Если имеется эмпирический ряд распределения, то необходимо найти функцию
Слайд 44
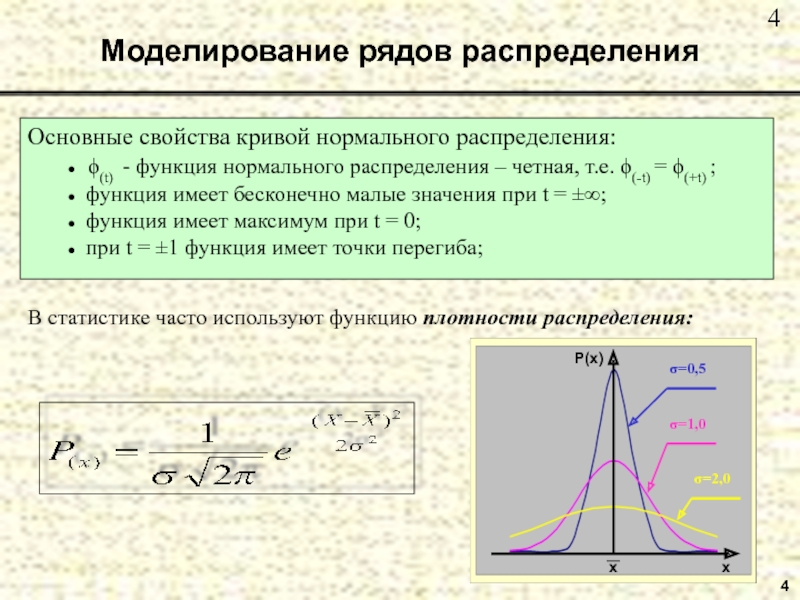
Моделирование рядов распределения
Основные свойства кривой нормального распределения:
● ϕ(t) - функция нормального
● функция имеет бесконечно малые значения при t = ±∞;
● функция имеет максимум при t = 0;
● при t = ±1 функция имеет точки перегиба;
Слайд 55
Моделирование рядов распределения
Связь между теоретической нормированной функцией нормального распределения и теоретической
где А – коэффициент нормировки, который для распределения с равными интервалами Δx=k рассчитывается с помощью соотношения:
fi - частота i-го интервала ряда.
Слайд 66
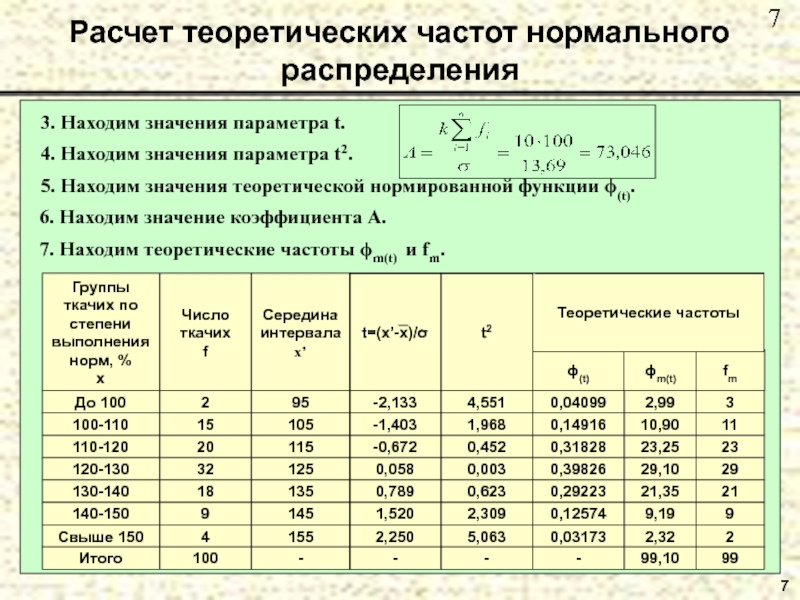
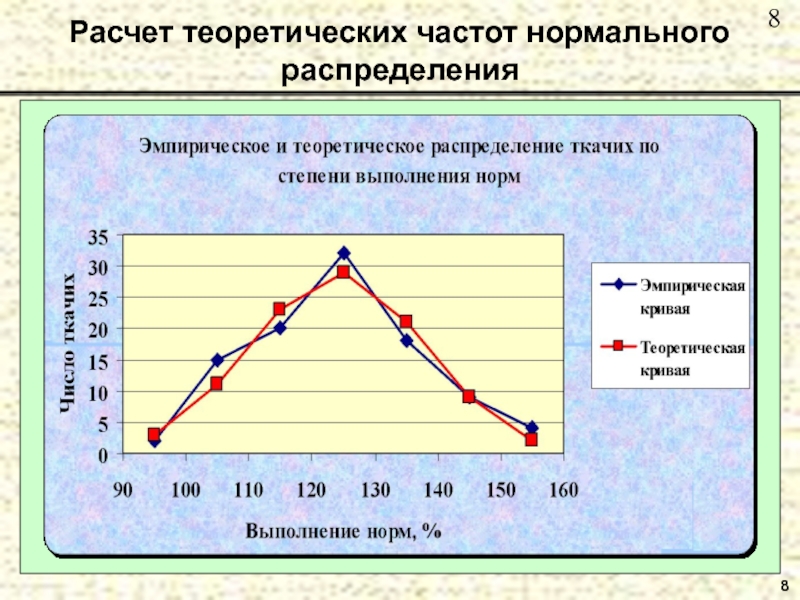
Расчет теоретических частот нормального распределения
Пример. В приведенной таблице показано распределение ткачих
Слайд 77
Расчет теоретических частот нормального распределения
3. Находим значения параметра t.
4. Находим значения
5. Находим значения теоретической нормированной функции ϕ(t).
6. Находим значение коэффициента А.
7. Находим теоретические частоты ϕm(t) и fm.
Слайд 99
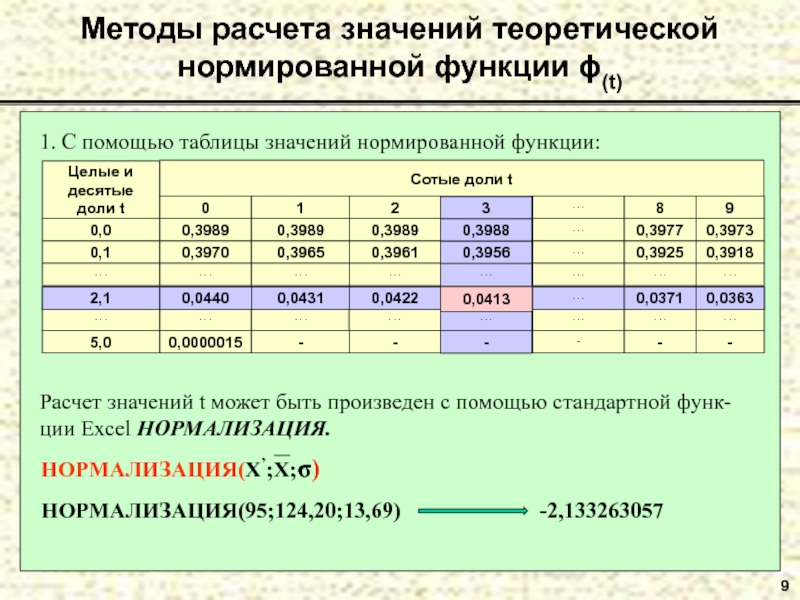
Методы расчета значений теоретической нормированной функции ϕ(t)
1. С помощью таблицы значений
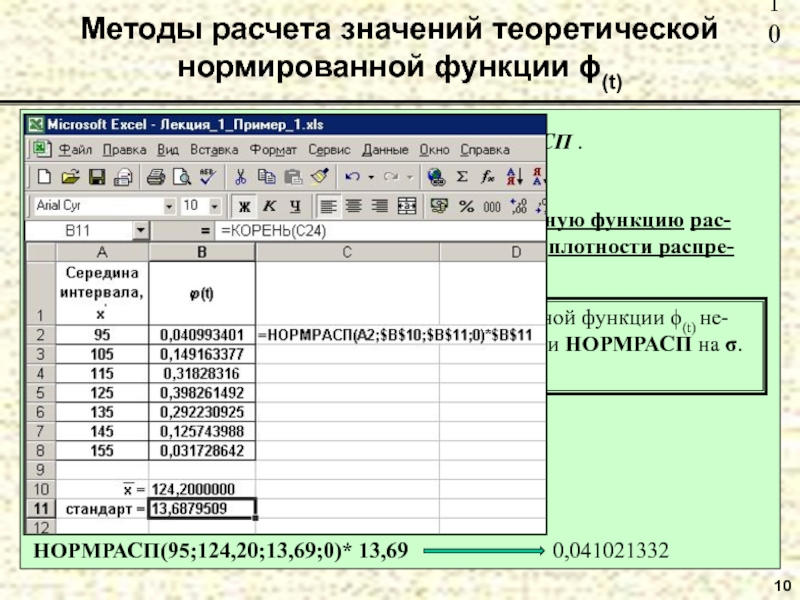
Слайд 1010
Методы расчета значений теоретической нормированной функции ϕ(t)
2. С помощью стандартной функции
Для получения значений теоретической нормированной функции ϕ(t) не-обходимо домножить возвращаемое значение функции НОРМРАСП на σ.
Слайд 1111
Критерий согласия Пирсона
Критерий согласия Пирсона:
Для найденного значения критерия согласия Пирсона
При P(χ2)>0,5 считается, что эмпирическое и теоретическое распределе-ния близки, при P(χ2)∈[0,2;0,5] совпадение удовлетворительное, в осталь-ных случаях – недостаточное.
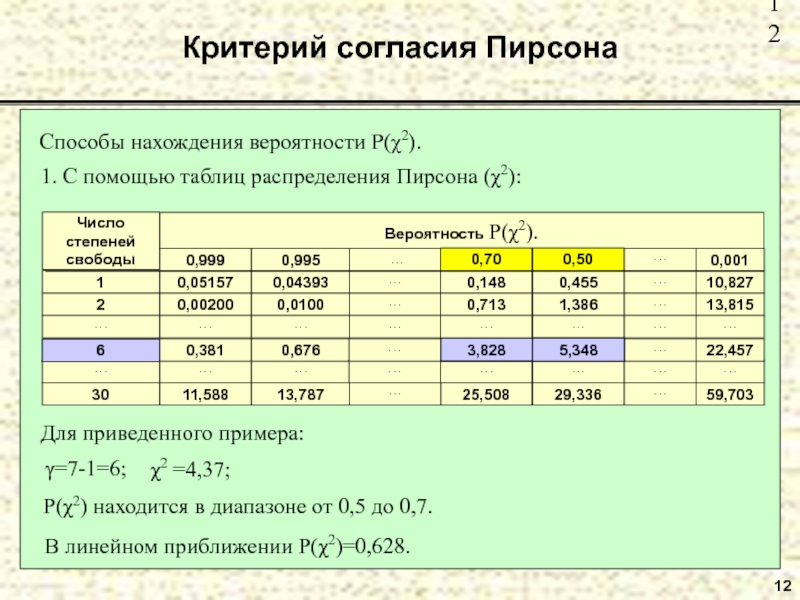
Слайд 1212
Критерий согласия Пирсона
Способы нахождения вероятности P(χ2).
В линейном приближении Р(χ2)=0,628.
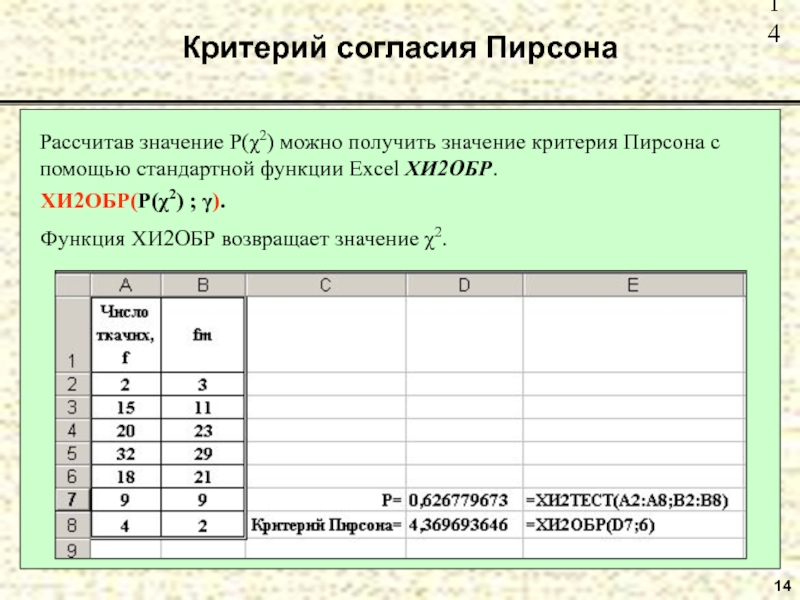
Слайд 1414
Критерий согласия Пирсона
Рассчитав значение P(χ2) можно получить значение критерия Пирсона с
ХИ2ОБР(P(χ2) ; γ).
Функция ХИ2ОБР возвращает значение χ2.
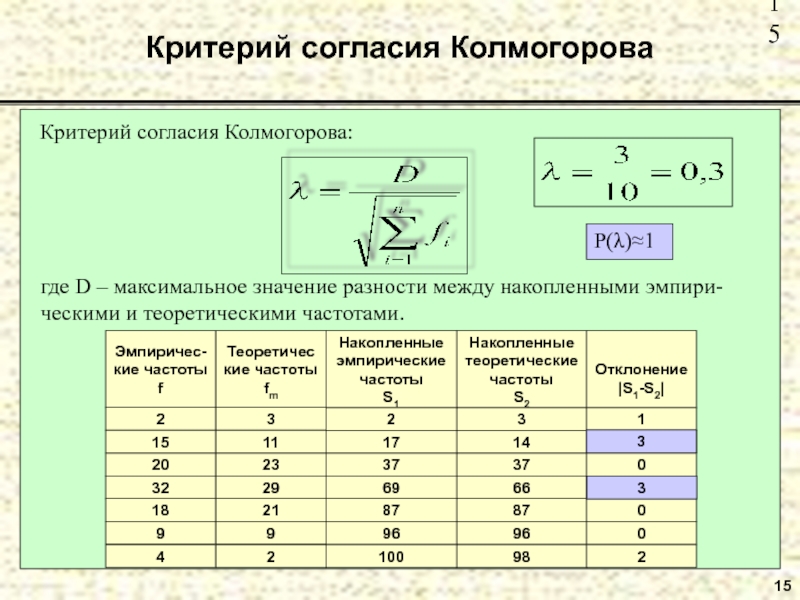
Слайд 1515
Критерий согласия Колмогорова
Критерий согласия Колмогорова:
где D – максимальное значение разности
Слайд 1616
Критерий согласия Романовского
Критерий согласия Романовского:
где χ2 – критерий Пирсона, γ
При С<3 различие несущественно, что позволяет считать эмпирическое распределение близким к нормальному.