- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математический анализ. Множества презентация
Содержание
Слайд 2Бер Л.М. Введение в анализ.
ОСНОВНАЯ ЛИТЕРАТУРА
Пискунов Н.С. Дифференциальное и интегральное исчисление. Т. 1. – М.: ИНТЕГРАЛ-ПРЕСС, 1997.
Пискунов Н.С. Дифференциальное и интегральное исчисление. Т. 2. – М.: ИНТЕГРАЛ-ПРЕСС, 1998.
Кудрявцев Л.Д. Краткий курс математического анализа. Т. 1., Т. 2. – М.: ФИЗМАТЛИТ, 2002.
Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1975.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Герасимович А.И., Рысюк Н.А. Математический анализ. Справочное пособие. Ч.1. – Минск: Вышэйшая школа, 1989.
Герасимович А.И., Кеда Н.П., Сугак М.Б. Математический анализ. Справочное пособие. Ч.2. – Минск: Вышэйшая школа, 1990.
Марон И.А. Дифференциальное и интегральное исчисление в примерах и задачах. – М.: Наука, 1973.
Каплан И.А. Практические занятия по высшей математике. Ч.2. – Харьков: Вища школа, 1973.
Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П. Математический анализ в примерах и задачах. Т. 1,2 – Издательское объединение «Вища школа», 1977.
Подскребко Э.Н., Пестова Н.Ф. Дифференциальное исчисление функции нескольких переменных. Томск: изд-во ТПУ, 1997.
Слайд 3Бер Л.М. Введение в анализ.
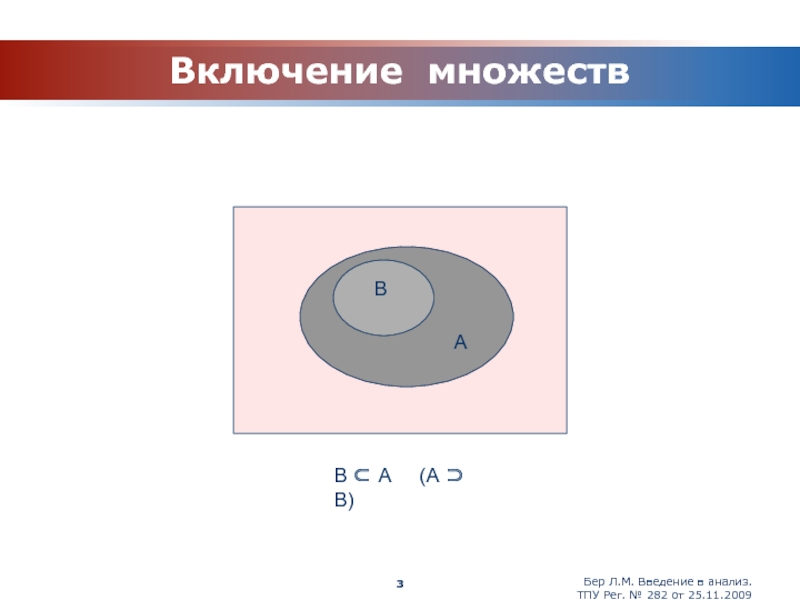
Включение множеств
В
А
В ⊂ А (А ⊃ В)
Слайд 4Бер Л.М. Введение в анализ.
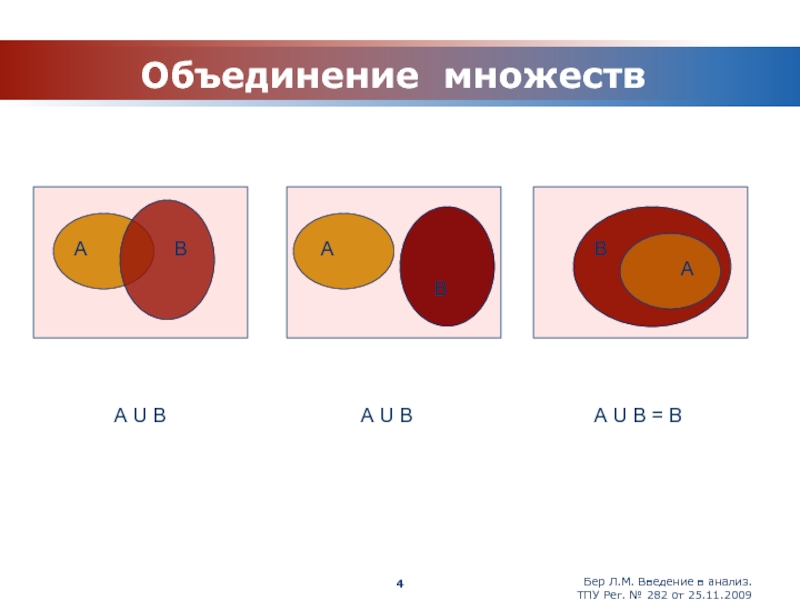
Объединение множеств
А U В
А U В
А U В = В
А
А
А
В
В
В
Слайд 5Бер Л.М. Введение в анализ.
Пересечение множеств
А
А
А
А
А
А
U
U
U
В
В
В
В
В =
∅
В = A
Слайд 6Бер Л.М. Введение в анализ.
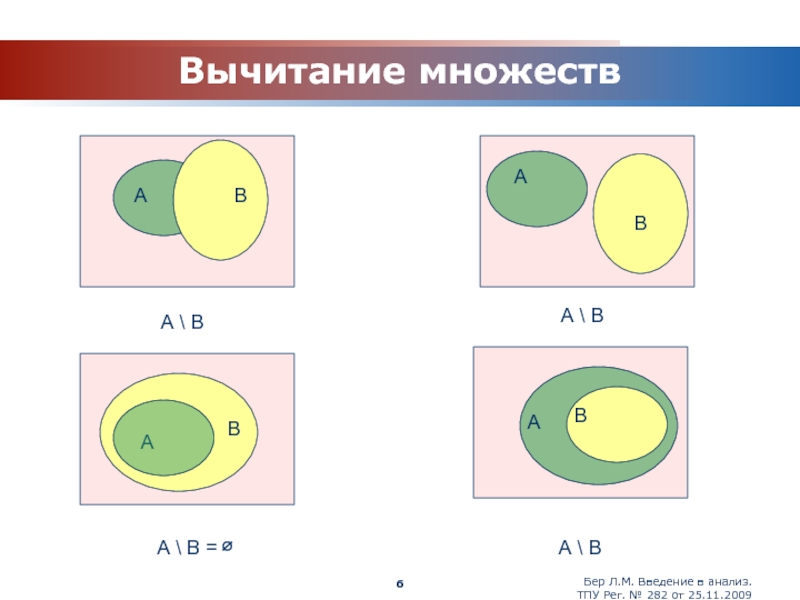
Вычитание множеств
А \ В
А \ В = ∅
А \ В
А \ В
А
А
А
А
В
В
В
В
Слайд 7Бер Л.М. Введение в анализ.
Числовые множества
1. N, Z, Q, I, R, R×R, C.
2. Подмножества вещественных чисел:
Пусть .
Отрезок, сегмент: ;
Интервал: ;
Полуинтервал: , ;
Замкнутый луч: , ;
Открытый луч: , .
Определение. Пусть x0 ∈ R, ε > 0. Интервал (x0-ε, x0+ε) будем называть ε-окрестностью точки x0 .
Обозначение: U(x0,ε)= (x0-ε, x0+ε)= {x ∈ R | |x - x0|<ε}.
Слайд 8Бер Л.М. Введение в анализ.
Числовые множества
R ∪ {+∞, –∞} =
Пусть ε > 0. Тогда
U(+∞,ε)=(1/ε; +∞)∪{+∞}={x∈ | x > 1/ε };
U(–∞,ε)=(–∞; –1/ε)∪{–∞}={x∈ | x < – 1/ε };
U(∞,ε)=(–∞; –1/ε)∪(1/ε; +∞)∪{∞}={x∈ | |x|> 1/ε }.