Курс геометрии за 8 класс презентация

Содержание

1. Курс геометрии за 8 класс
2. Содержание Четырехугольники Многоугольники Параллелограмм Трапеция Теорема Фалеса
3. А В С D
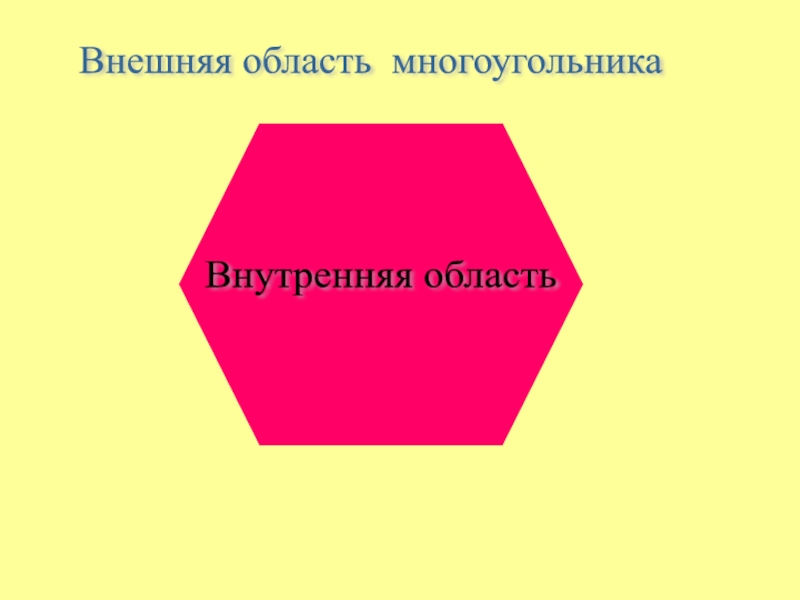
4. Внутренняя область Внешняя область многоугольника
5. Многоугольник называется выпуклым, если он лежит
6. Четырехугольник Каждый четырехугольник имеет: четыре
7. Параллелограмм
8. Признаки параллелограмма Если в четырехугольнике
9. Трапеция Трапецией называется четырехугольник, у которого две
10. Если на одной из двух прямых отложены
11. Прямоугольник Прямоугольником называется параллелограмм, у которого все
12. Ромб Ромбом называется параллелограмм, у
13. Квадратом называется прямоугольник , у которого все
14. а Две точки
15. Фигура называется симметричной относительно прямой а,
16. Две точки и
17. Фигура называется симметричной относительно точки О, если
18. Людям часто
19. Понятие площади. Свойства площадей. Площадь –
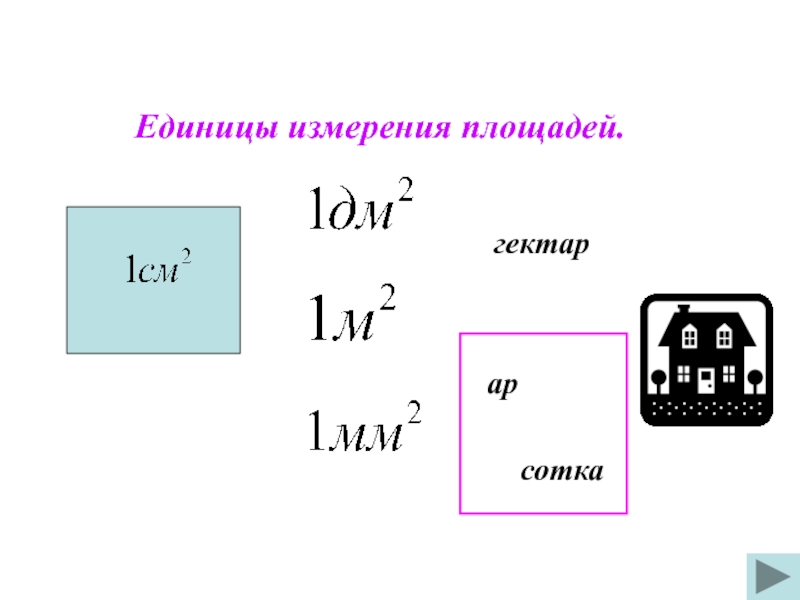
20. Единицы измерения площадей. гектар ар сотка
21. Понятие площади. Свойства площадей. Свойства площадей.
22. Понятие площади. Свойства площадей. 3. Площадь квадрата равна квадрату его стороны.
23. Площадь прямоугольника. Теорема. Площадь прямоугольника
24. Площадь параллелограмма. Теорема. Площадь параллелограмма равна
25. Площадь треугольника. Теорема. Площадь треугольника равна
26. Площадь треугольника. Прямоугольный треугольник. а
27. Площадь трапеции. Теорема. Площадь трапеции равна произведению полусуммы ее оснований на высоту.
28. В прямоугольном треугольнике квадрат гипотенузы равен сумме
29. Определение подобных треугольников Два треугольника называются подобными,
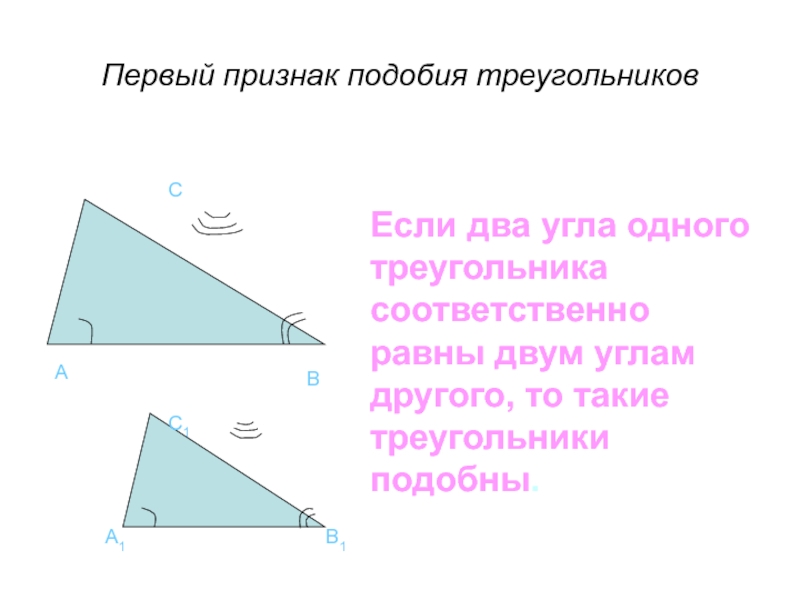
30. A B C
31. Второй признак подобия треугольников A C
32. Третий признак подобия треугольников
33. Средней линией треугольника называется отрезок, соединяющий
34. Средняя линия треугольника параллельна одной из его
35. Медианы треугольника пересекаются в
36. Высота прямоугольного треугольника, проведенная из прямого угла,
37. Высота прямоугольного треугольника, проведенная из вершины
38. Катет прямоугольного треугольника есть среднее пропорциональное для
39. Соотношения между сторонами и углами прямоугольного треугольника А В С
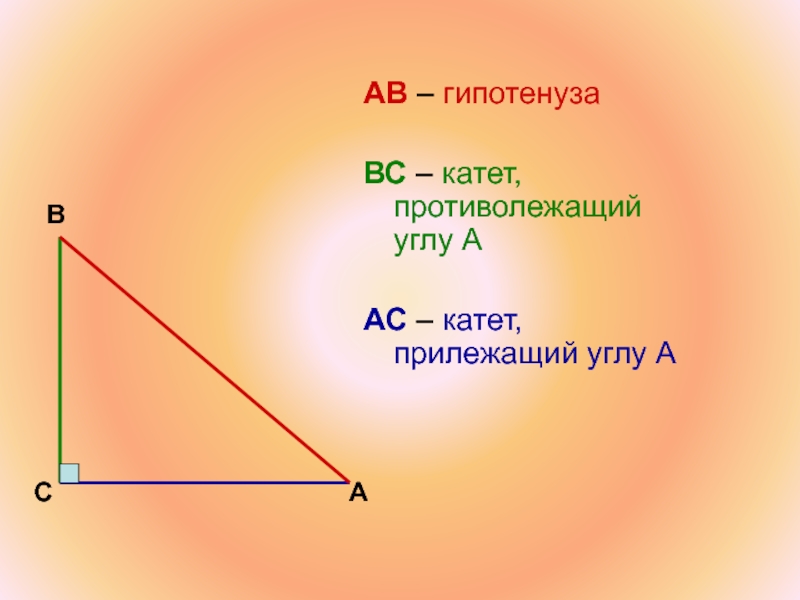
40. АВ – гипотенуза ВС –
41. Синус острого угла прямоугольного треугольника Синусом острого
42. Косинус острого угла прямоугольного треугольника Косинусом
43. Тангенс острого угла прямоугольного треугольника Тангенсом
44. Тригонометрические тождества Основное тригонометрическое тождество: 2)
45. Значения синуса, косинуса и тангенса угла
46. Значения синуса, косинуса и тангенса угла
47. Значения синуса, косинуса и тангенса угла

Содержание Четырехугольники Многоугольники Параллелограмм Трапеция Теорема Фалеса Прямоугольник Ромб Квадрат Осевая и центральная симметрия Площадь Свойства площадей Площадь прямоугольника Площадь параллелограмма Площадь треугольника Площадь

Слайд 1Геометрия 8 класс.

Слайд 2Содержание
Четырехугольники
Многоугольники
Параллелограмм
Трапеция
Теорема Фалеса
Прямоугольник
Ромб
Квадрат
Осевая и центральная симметрия
Площадь
Свойства площадей
Площадь

прямоугольника
Площадь параллелограмма
Площадь треугольника
Площадь трапеции
Теорема Пифагора
Подобные треугольники
Определение подобных треугольников
Признаки подобия треугольников
Средняя линия треугольника
Соотношения между сторонами и углами прямоугольного треугольника

Слайд 3А
В
С
D
E
F
Фигура, составленная из отрезков АВ,

ВС, СD, ..., EF, FA так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек, называется многоугольником.

Отрезки AB, BC, CD,...EF - cтороны многоугольника

Сумма длин всех сторон называется периметром многоугольника AB+BC+CD+...+EF +АF=P ( периметр многоугольника)

Две вершины многоугольника, принадлежащие одной стороне, называются соседними.

Отрезок, соединяющий любые две несоседние вершины. называется диагональю многоугольника.

Слайд 4
Внутренняя область
Внешняя область многоугольника

Слайд 5
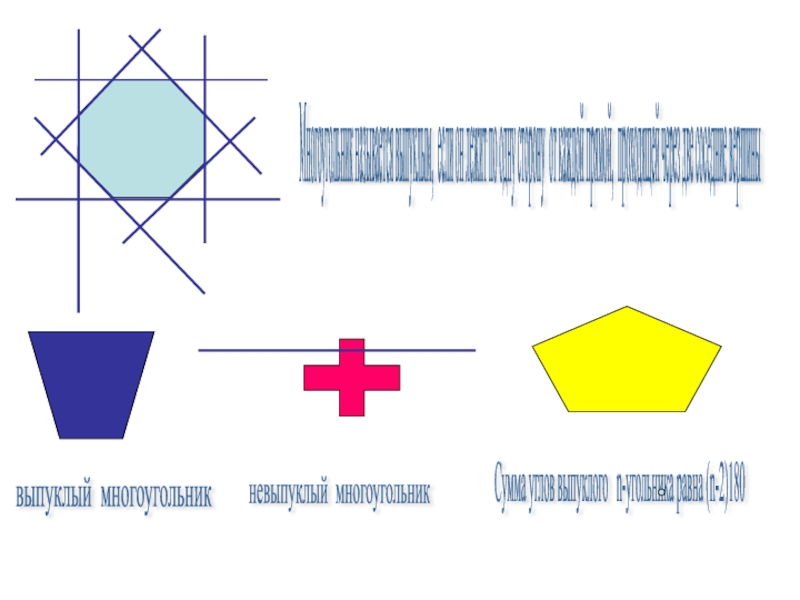
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой

прямой, проходящей через две соседние вершины

выпуклый многоугольник

невыпуклый многоугольник

Сумма углов выпуклого n-угольника равна (n-2)180

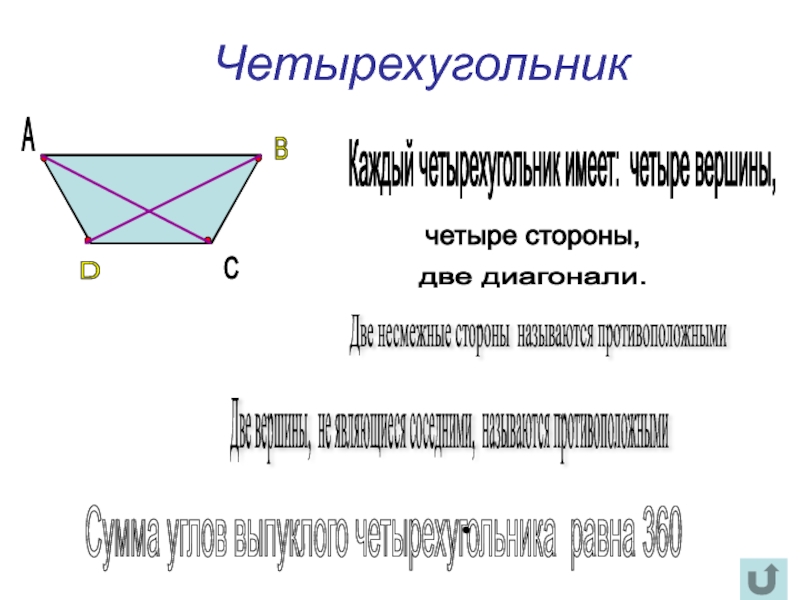
Слайд 6Четырехугольник

Каждый четырехугольник имеет: четыре вершины,

четыре стороны,
две диагонали.
Две

несмежные стороны называются противоположными

Две вершины, не являющиеся соседними, называются противоположными

Сумма углов выпуклого четырехугольника равна 360

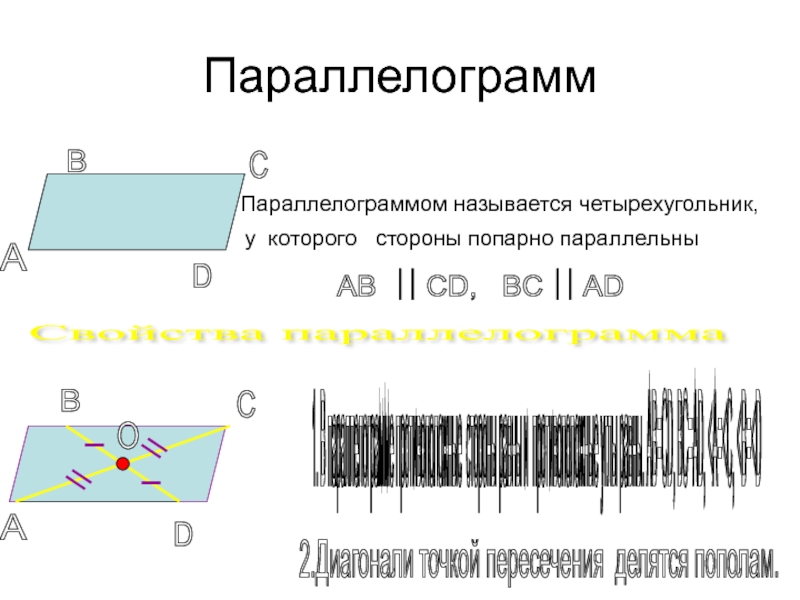
Слайд 7Параллелограмм

Параллелограммом называется четырехугольник,
у которого стороны попарно параллельны

AB CD, BC AD

Свойства параллелограмма

1. В параллелограмме противоположные стороны равны и противоположные углы равны. AB=CD, BC=AD,

2.Диагонали точкой пересечения делятся пополам.

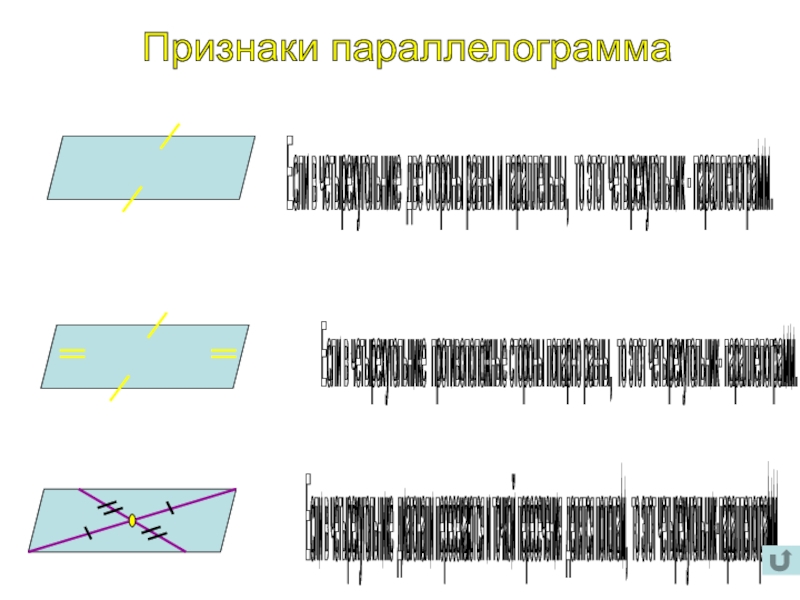
Слайд 8Признаки параллелограмма

Если в четырехугольнике две стороны равны и параллельны, то

этот четырехугольник - параллелограмм.

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник- параллелограмм.

Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник-параллелограмм.

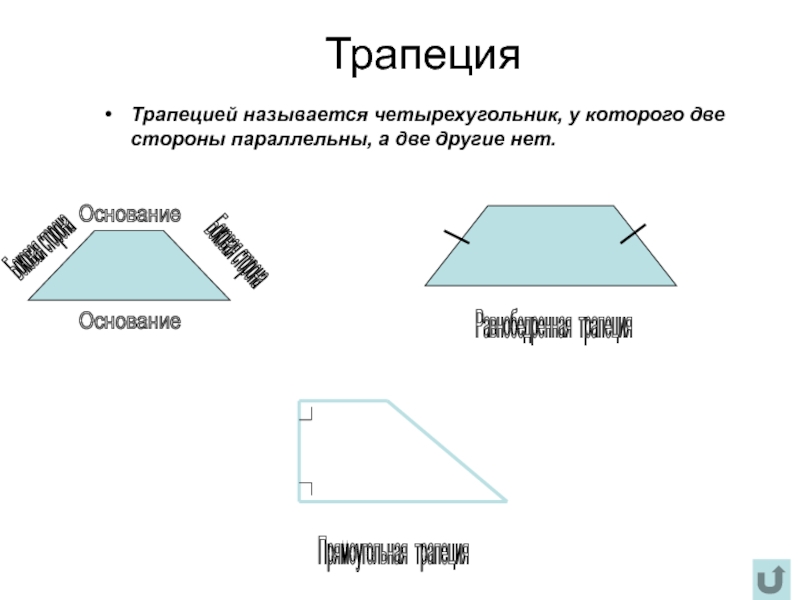
Слайд 9Трапеция
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие

нет.

Основание

Боковая сторона

Равнобедренная трапеция

Прямоугольная трапеция

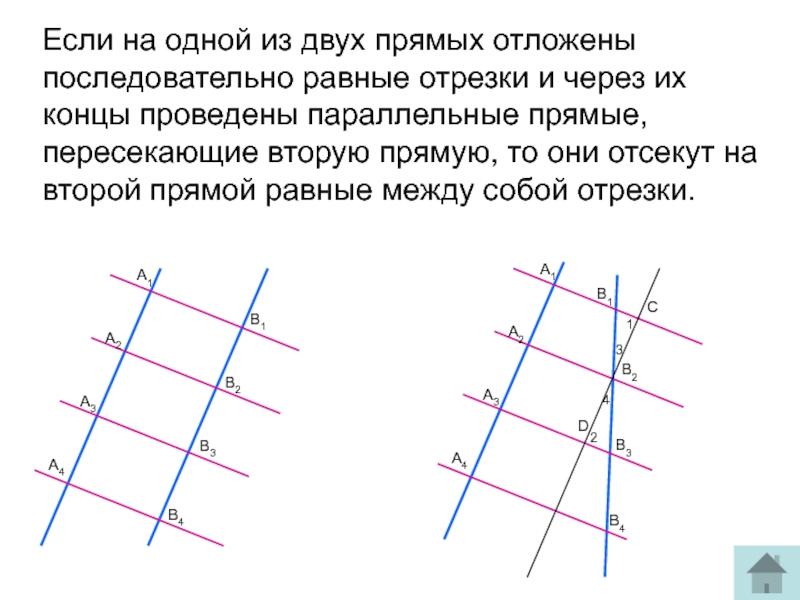
Слайд 10Если на одной из двух прямых отложены последовательно равные отрезки и

через их концы проведены параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

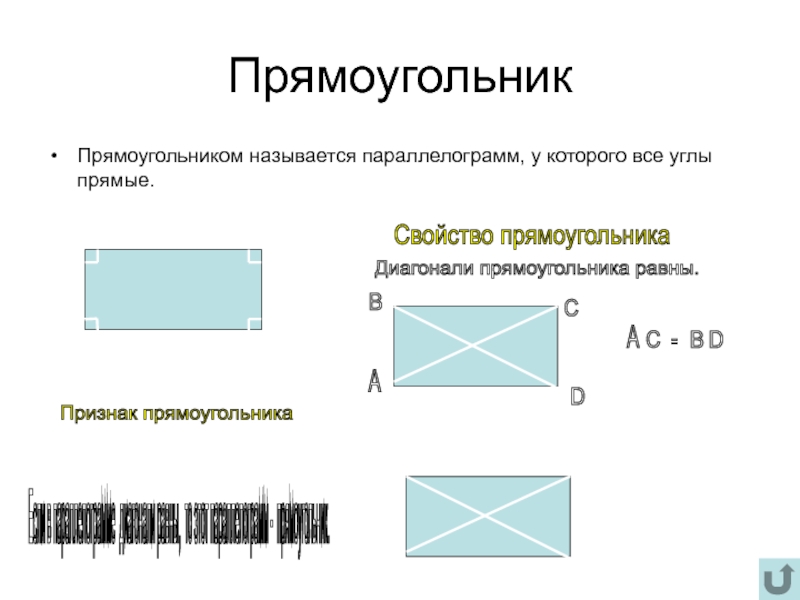
Слайд 11Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые.

Свойство прямоугольника
Диагонали прямоугольника

равны.

Признак прямоугольника

Если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник.

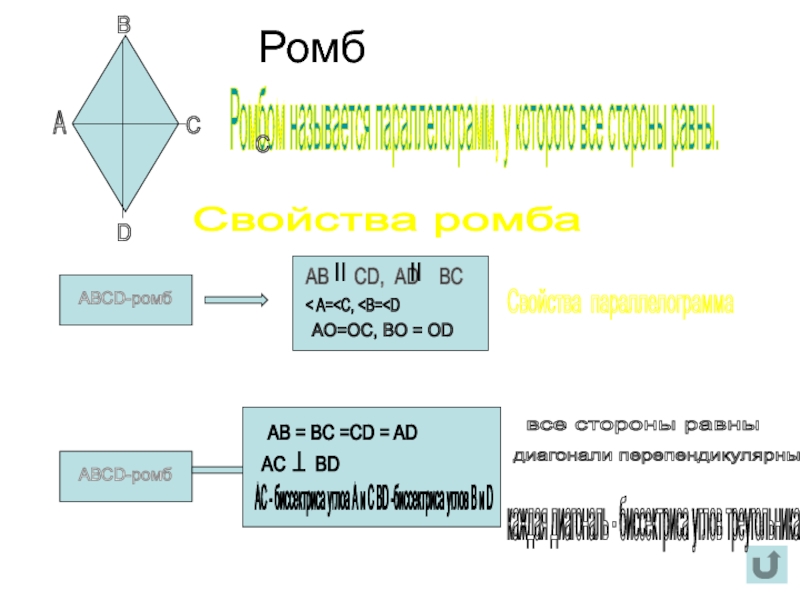
Слайд 12Ромб

Ромбом называется параллелограмм, у которого все стороны равны.
Свойства ромба

АВ

СD, АD ВС

< A=

AO=OC, BO = OD

Свойства параллелограмма

все стороны равны

диагонали перепендикулярны

каждая диагональ - биссектриса углов треугольника

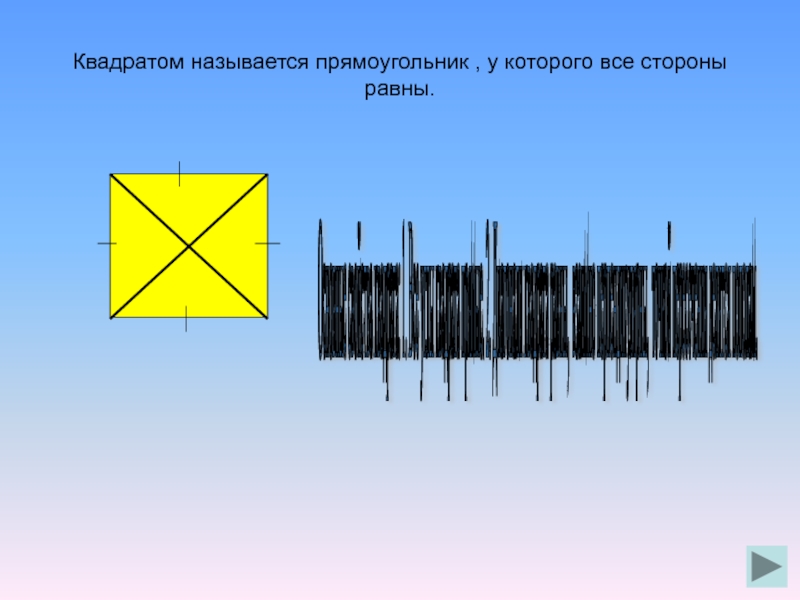
Слайд 13Квадратом называется прямоугольник , у которого все стороны равны.

Основные свойства квадрата:

1. Все углы квадрата прямые. 2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам.

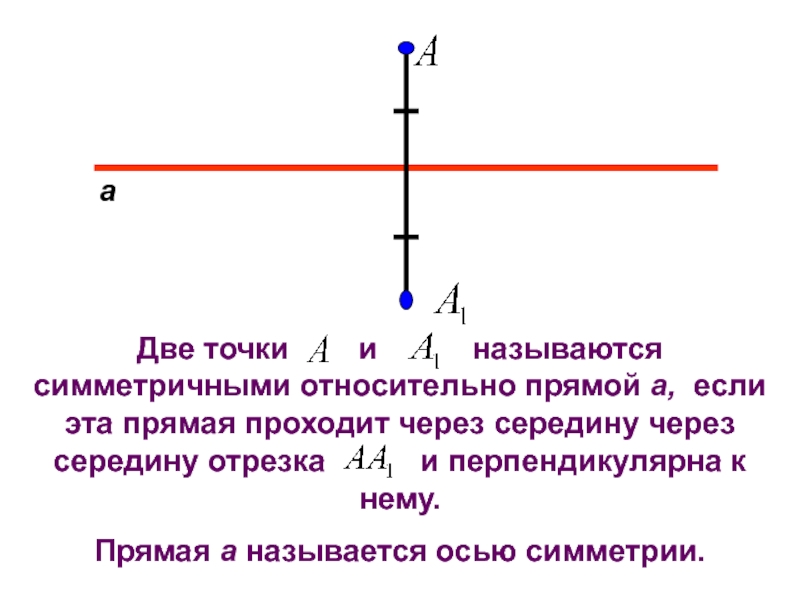
Слайд 14а

Две точки и

называются симметричными относительно прямой а, если эта прямая проходит через середину через середину отрезка и перпендикулярна к нему.
Прямая а называется осью симметрии.

Слайд 15
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры

симметричная ей точка относительно прямой а также принадлежит этой фигуре.
Прямая а называется осью симметрии фигуры.

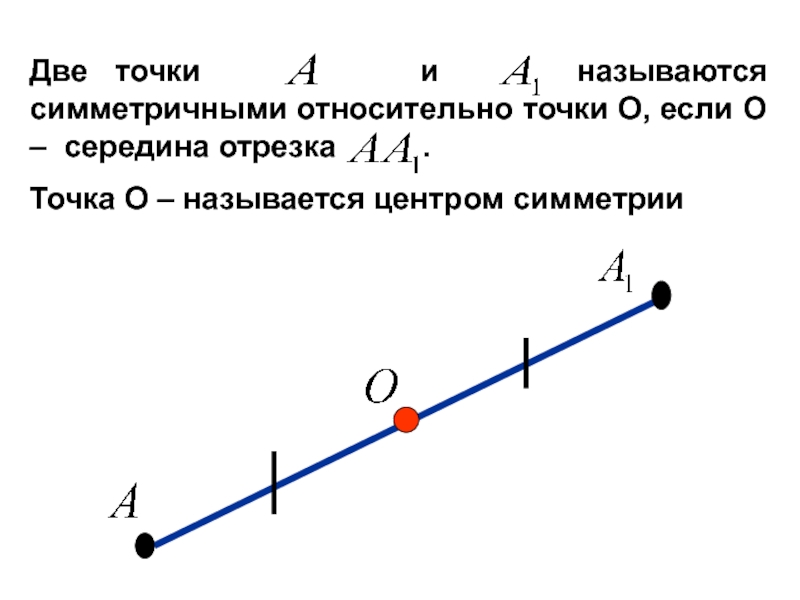
Слайд 16Две точки и называются симметричными относительно

точки О, если О – середина отрезка .
Точка О – называется центром симметрии

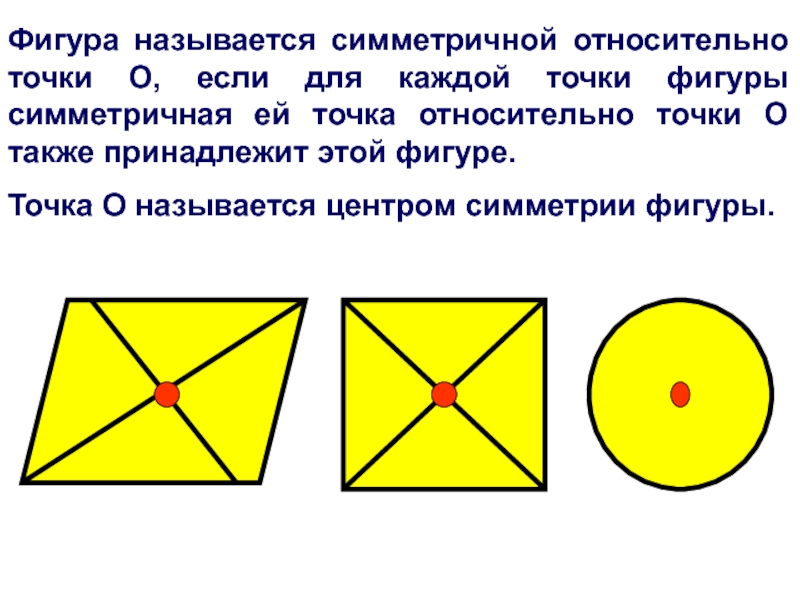
Слайд 17Фигура называется симметричной относительно точки О, если для каждой точки фигуры

симметричная ей точка относительно точки О также принадлежит этой фигуре.
Точка О называется центром симметрии фигуры.

Слайд 18

Людям часто приходилось делить землю по берегам Нила

на участки. Подсчитывать площадь трудно, берега извилисты, границы участка неровные. И люди постепенно научились измерять такие площади, разбивая их на прямоугольные и треугольные участки (17 век до н. э.)

Происхождение науки геометрии.

Для чего нужно было измерять площади?

Слайд 19 Понятие площади. Свойства площадей.
Площадь – положительное число, которое показывает сколько

раз единица измерения или ее часть укладывается в данной фигуре.

Слайд 20

Единицы измерения площадей.
гектар
ар
сотка

Слайд 21 Понятие площади. Свойства площадей.
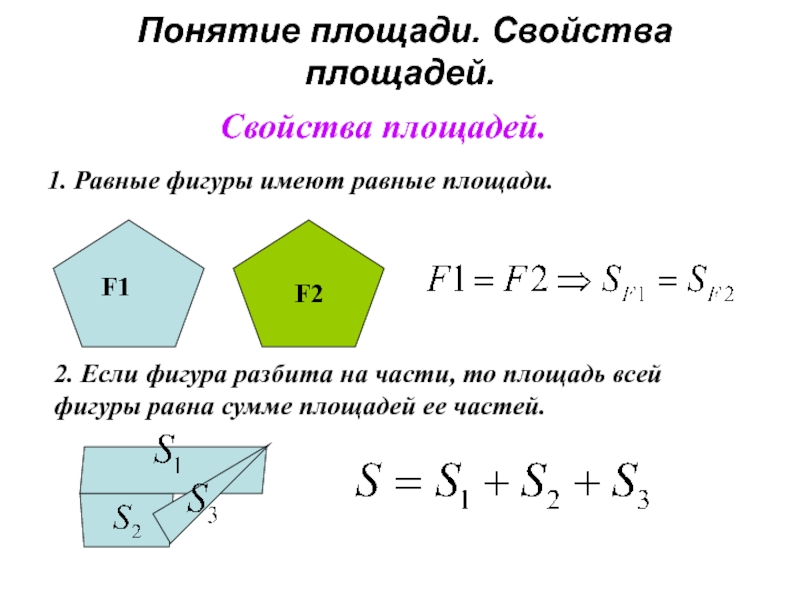
Свойства площадей.
1. Равные фигуры имеют равные площади.

2.

Если фигура разбита на части, то площадь всей фигуры равна сумме площадей ее частей.

Слайд 22 Понятие площади. Свойства площадей.
3. Площадь квадрата равна квадрату его стороны.

Слайд 23Площадь прямоугольника.
Теорема.
Площадь прямоугольника равна произведению смежных сторон.

А
В
С
D

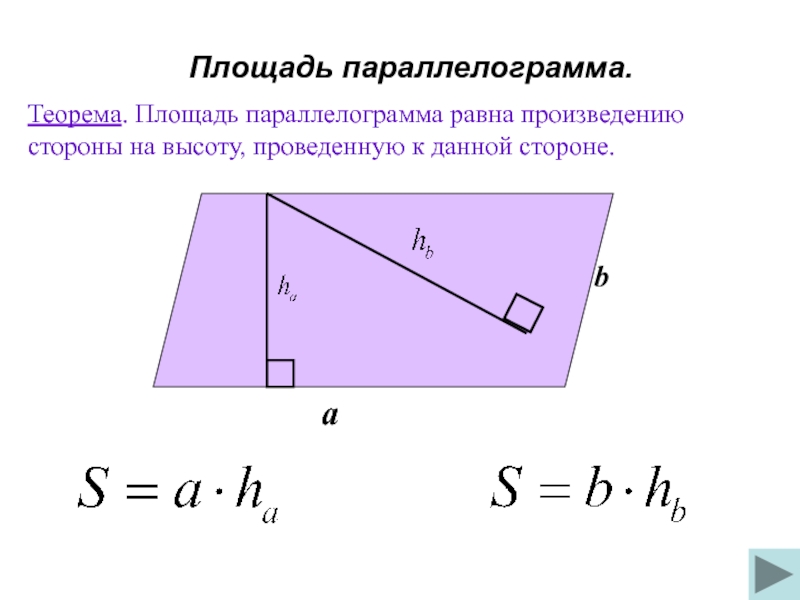
Слайд 24 Площадь параллелограмма.
Теорема. Площадь параллелограмма равна произведению стороны на высоту, проведенную

к данной стороне.

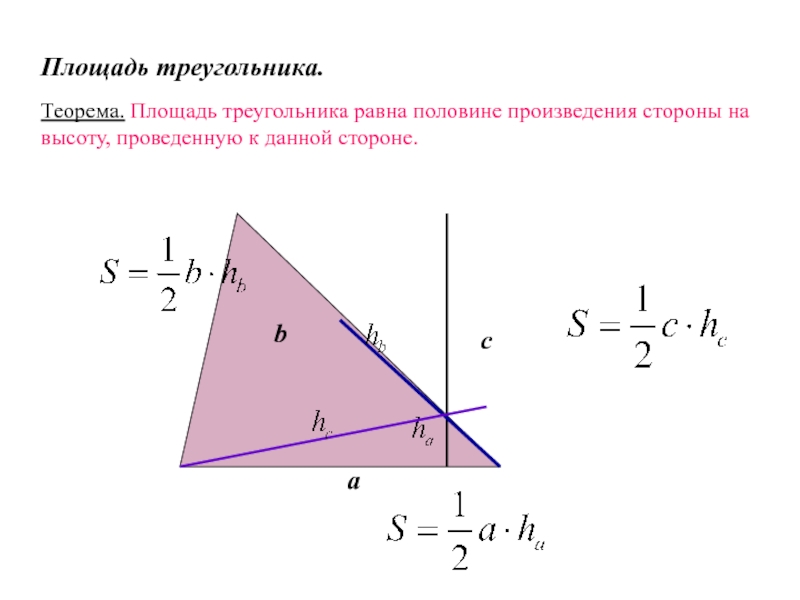
Слайд 25 Площадь треугольника.
Теорема. Площадь треугольника равна половине произведения стороны на высоту,

проведенную к данной стороне.

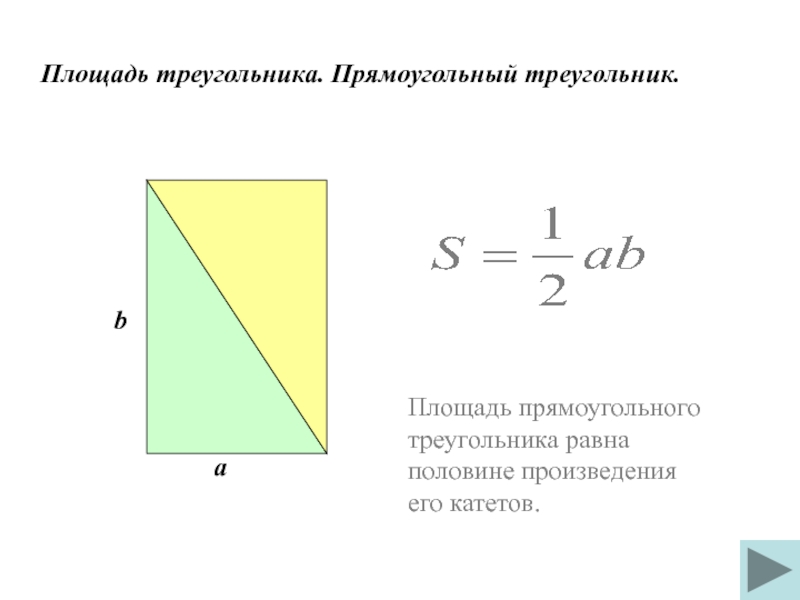
Слайд 26 Площадь треугольника. Прямоугольный треугольник.

а
b

Площадь прямоугольного треугольника равна половине произведения его

катетов.

Слайд 27 Площадь трапеции.
Теорема. Площадь трапеции равна произведению полусуммы ее оснований на

высоту.

Слайд 28В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
c²=a²+b²
С – гипотенуза
a,b

– катеты.

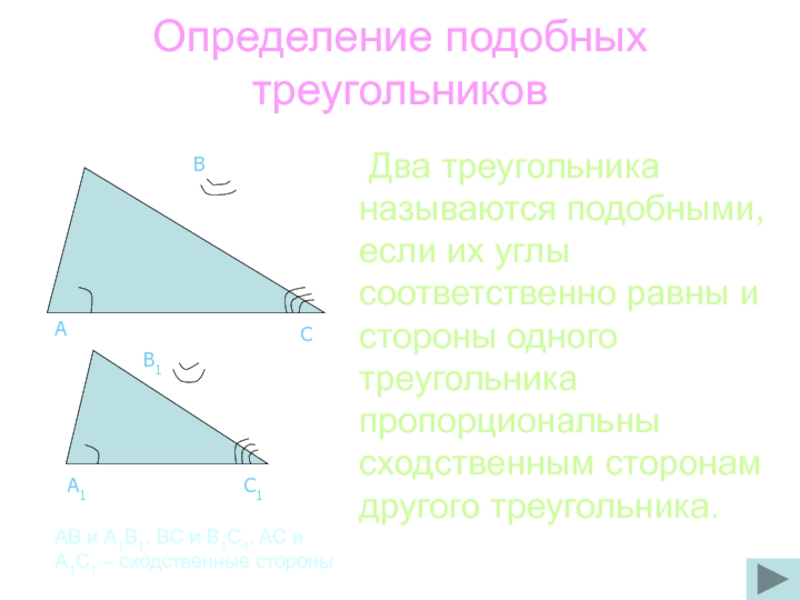
Слайд 29Определение подобных треугольников
Два треугольника называются подобными, если их углы соответственно равны

и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

AB и A1B1, BC и B1C1, AC и A1C1 – сходственные стороны

Слайд 30

A
B
C

A1
B1
C1

Если два угла одного треугольника соответственно равны двум углам другого, то

такие треугольники подобны.

Первый признак подобия треугольников

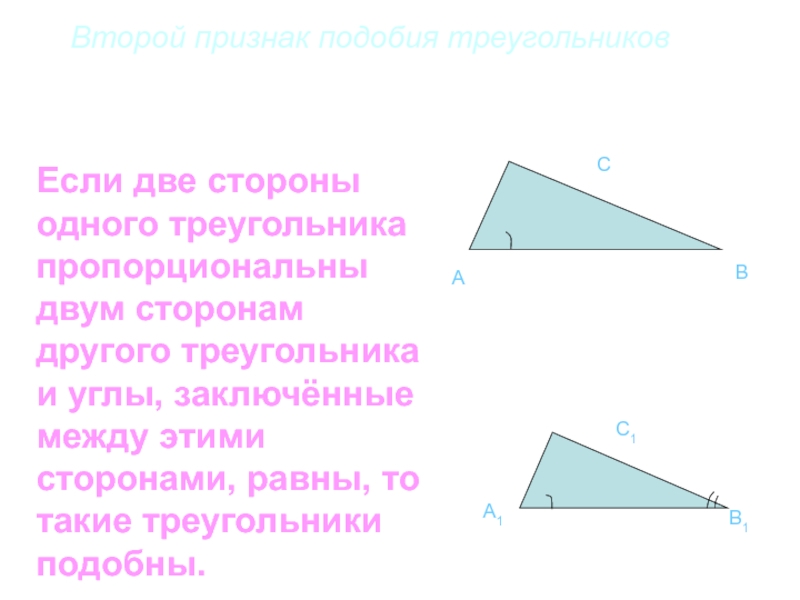
Слайд 31Второй признак подобия треугольников

A
C
A1
C1
B1

B
Если две стороны одного треугольника пропорциональны двум сторонам

другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.

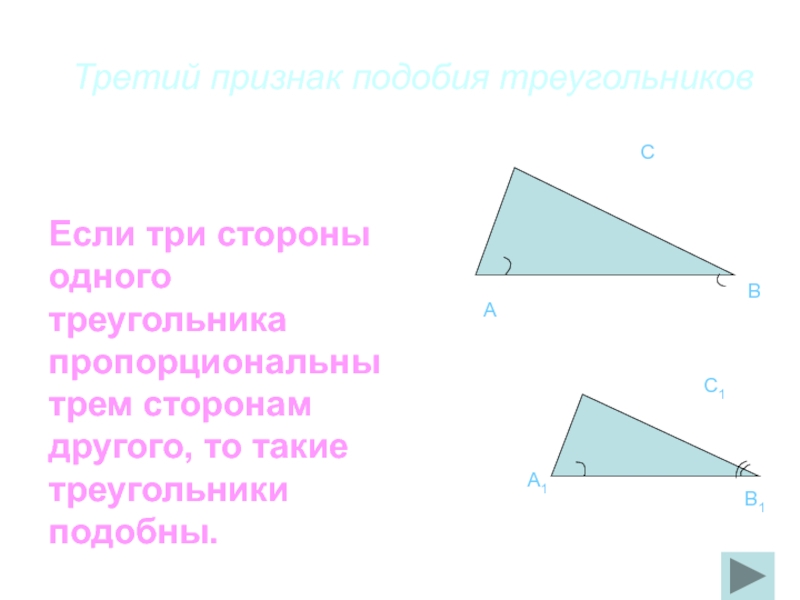
Слайд 32Третий признак подобия треугольников

A
C
B

A1
C1
B1
Если три стороны одного треугольника пропорциональны трем сторонам

другого, то такие треугольники подобны.

Слайд 33
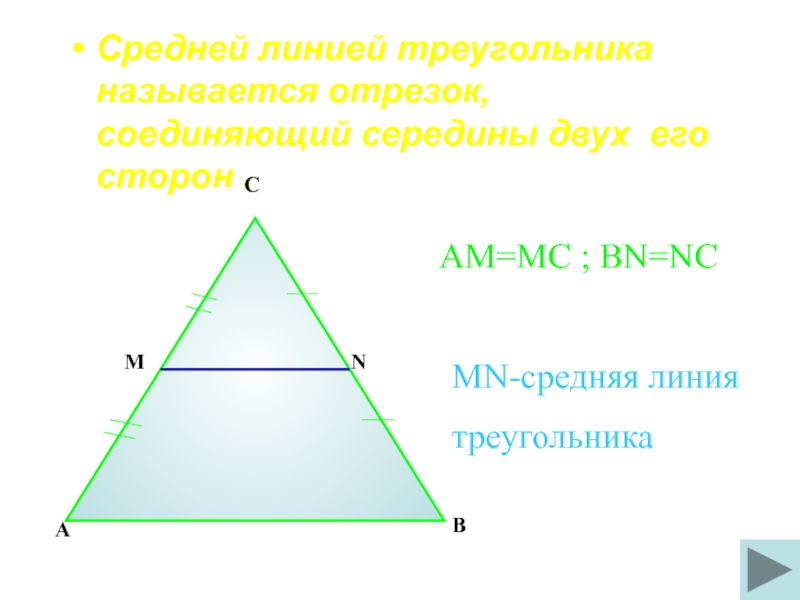
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон .

А
В
С
М
N
AM=MC

; BN=NC

MN-средняя линия
треугольника

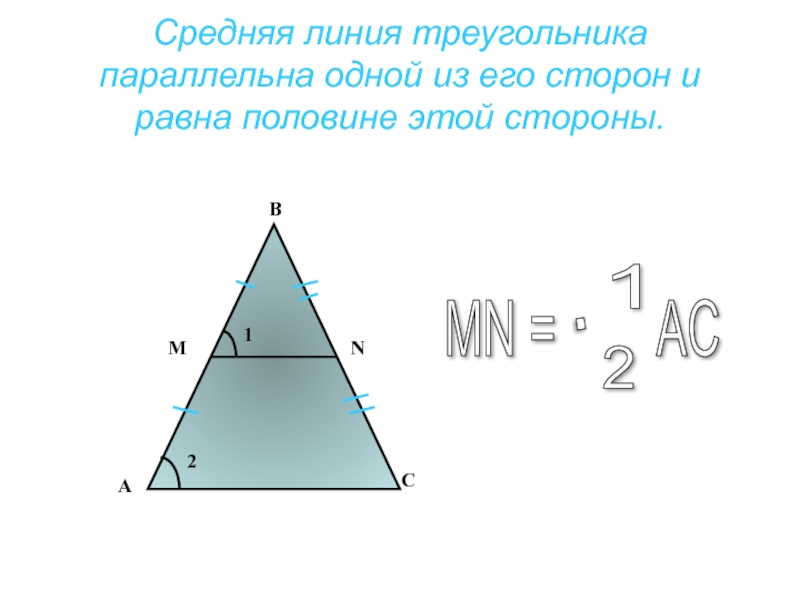
Слайд 34Средняя линия треугольника параллельна одной из его сторон и равна половине

этой стороны.

Слайд 35
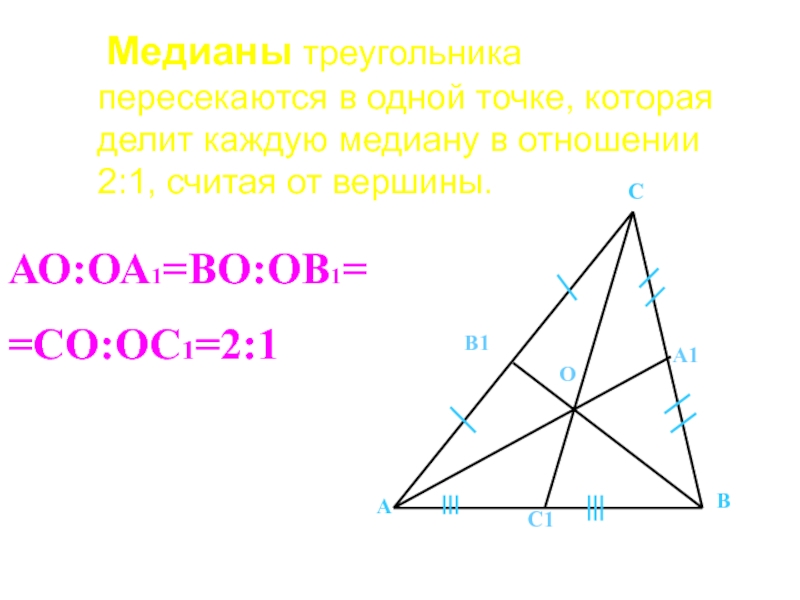
Медианы треугольника пересекаются в одной точке, которая делит каждую

медиану в отношении 2:1, считая от вершины.

С1

В1

А1

АО:ОА1=ВО:ОВ1=
=СО:ОС1=2:1

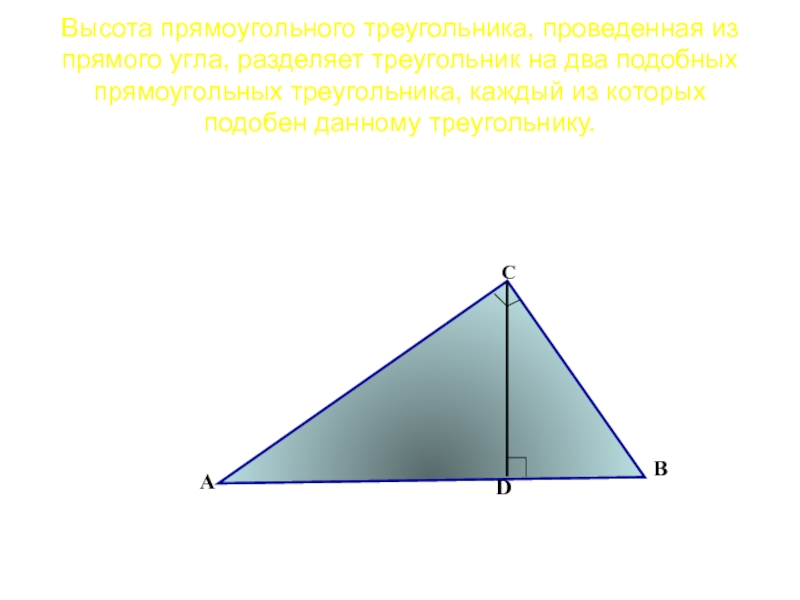
Слайд 36Высота прямоугольного треугольника, проведенная из прямого угла, разделяет треугольник на два

подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Слайд 37
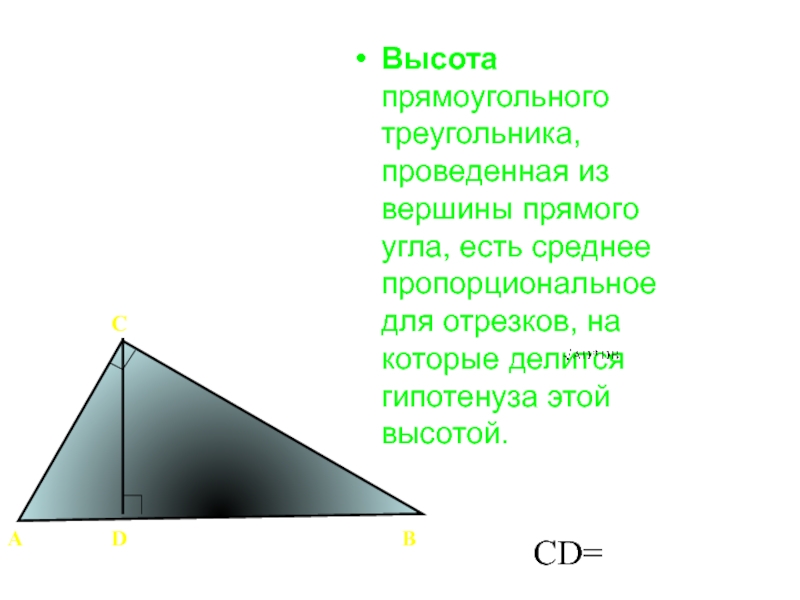
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное

для отрезков, на которые делится гипотенуза этой высотой.

CD=

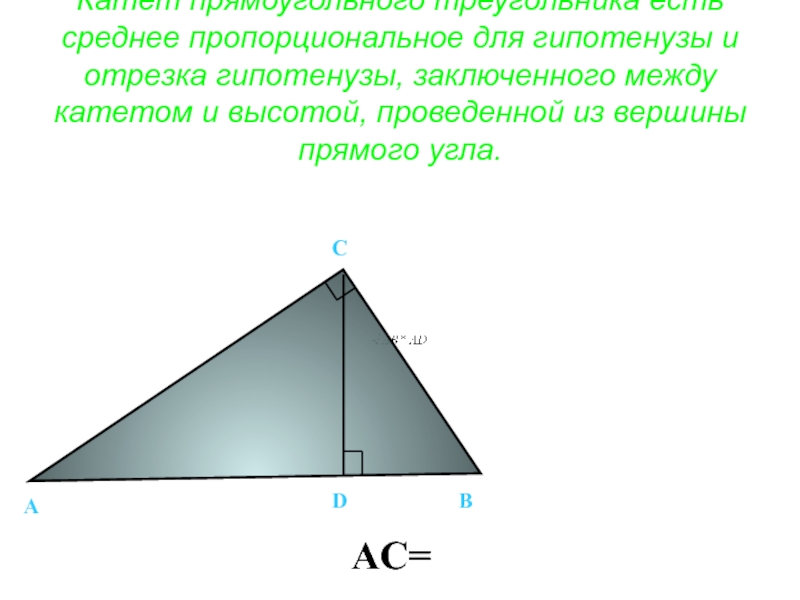
Слайд 38Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы,

заключенного между катетом и высотой, проведенной из вершины прямого угла.

AC=

Слайд 39Соотношения между сторонами и углами прямоугольного треугольника
А
В
С

Слайд 40
АВ – гипотенуза

ВС – катет, противолежащий углу А

АС – катет, прилежащий

углу А

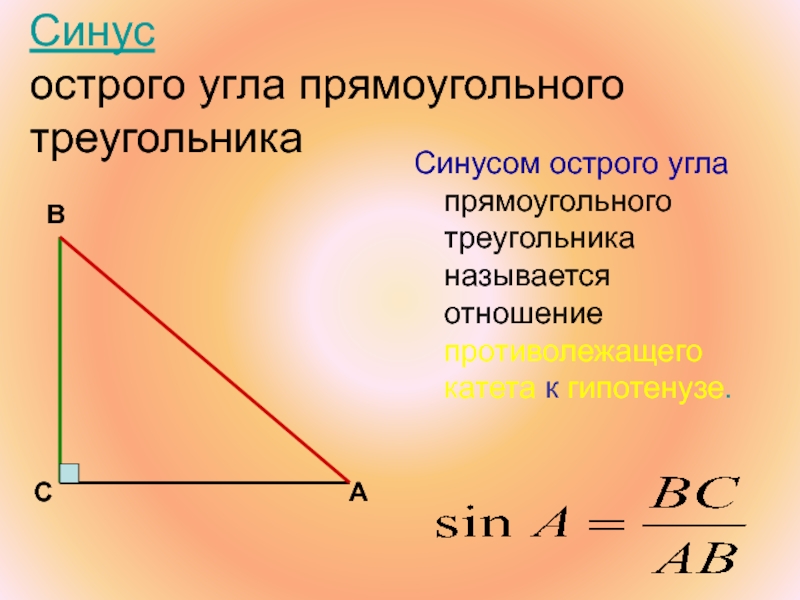
Слайд 41Синус острого угла прямоугольного треугольника
Синусом острого угла прямоугольного треугольника называется отношение противолежащего

катета к гипотенузе.

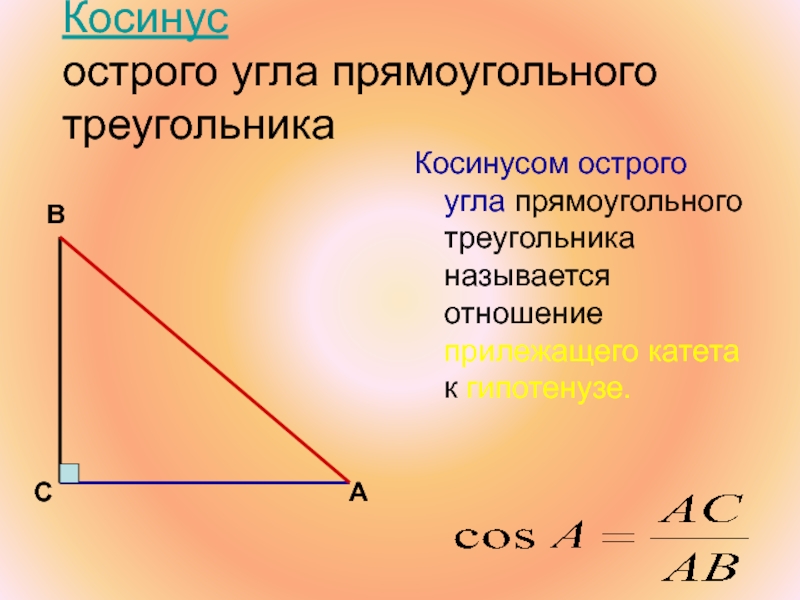
Слайд 42Косинус острого угла прямоугольного треугольника
Косинусом острого угла прямоугольного треугольника называется отношение

прилежащего катета к гипотенузе.

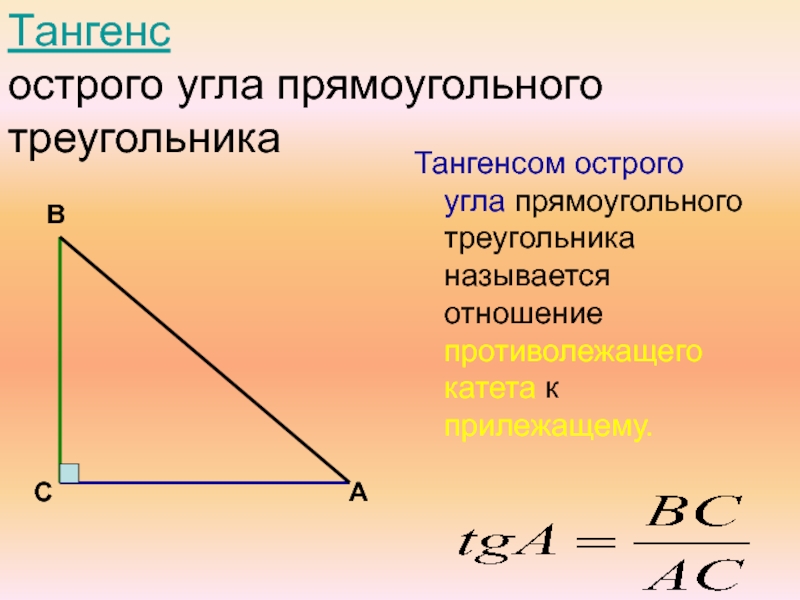
Слайд 43Тангенс острого угла прямоугольного треугольника
Тангенсом острого угла прямоугольного треугольника называется отношение

противолежащего катета к прилежащему.

Слайд 44Тригонометрические тождества
Основное тригонометрическое тождество:

2) Тангенс угла равен отношению синуса к косинусу

этого угла.

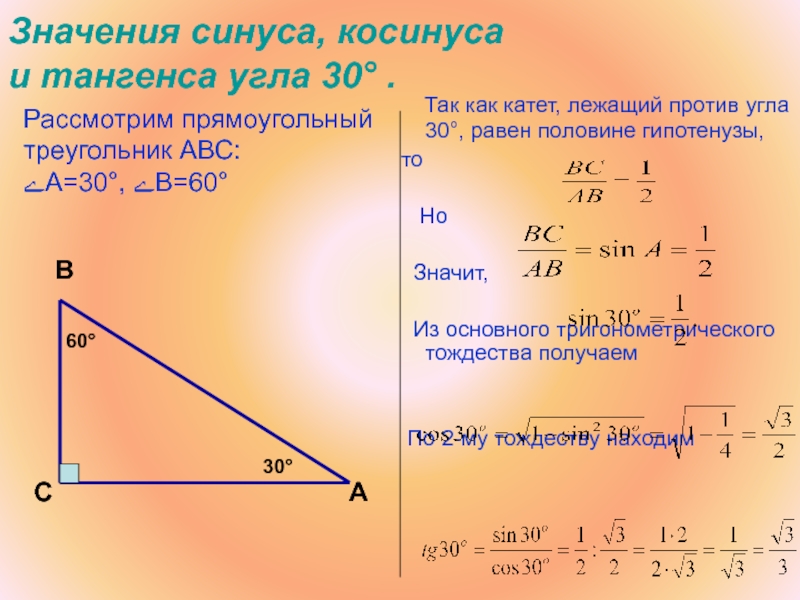
Слайд 45Значения синуса, косинуса и тангенса угла 30° .
Так как

катет, лежащий против угла 30°, равен половине гипотенузы,
то

Но

Значит,

Из основного тригонометрического тождества получаем

По 2-му тождеству находим

30°

Рассмотрим прямоугольный треугольник АВС:
ﮮА=30°, ﮮВ=60°

60°

Слайд 46Значения синуса, косинуса и тангенса угла 60°.
Так как катет,

лежащий против угла 30°, равен половине гипотенузы,
то

Или

Значит,

Из основного тригонометрического тождества получаем

По 2-му тождеству находим

30°

Рассмотрим прямоугольный треугольник АВС:
ﮮА=30°, ﮮВ=60°

60°

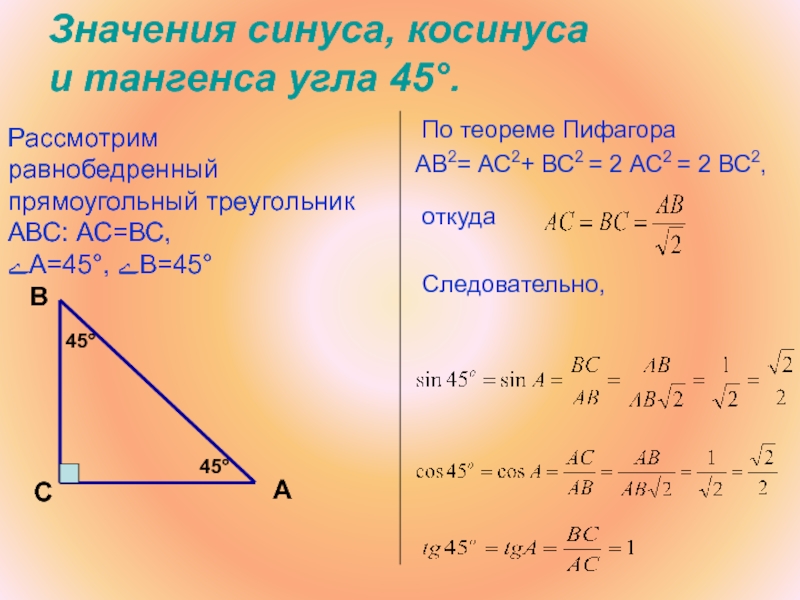
Слайд 47Значения синуса, косинуса и тангенса угла 45°.
По теореме Пифагора

АВ2= АС2+ ВС2 = 2 АС2 = 2 ВС2,

откуда

Следовательно,

45°

Рассмотрим равнобедренный прямоугольный треугольник АВС: АС=ВС,
ﮮА=45°, ﮮВ=45°

45°

Скачать презентацию

Курс геометрии за 8 класс презентация

Содержание

Слайд 1Геометрия 8 класс.

Слайд 3А В С D E F Фигура, составленная из отрезков АВ,

Слайд 4Внутренняя область Внешняя область многоугольника

Слайд 5Многоугольник называется выпуклым, если он лежит по одну сторону от каждой

Слайд 6Четырехугольник Каждый четырехугольник имеет: четыре вершины, четыре стороны, две диагонали. Две

Слайд 7Параллелограмм

Слайд 8Признаки параллелограмма Если в четырехугольнике две стороны равны и параллельны, то

Слайд 9ТрапецияТрапецией называется четырехугольник, у которого две стороны параллельны, а две другие

Слайд 10Если на одной из двух прямых отложены последовательно равные отрезки и

Слайд 11ПрямоугольникПрямоугольником называется параллелограмм, у которого все углы прямые.Свойство прямоугольника Диагонали прямоугольника

Слайд 12РомбРомбом называется параллелограмм, у которого все стороны равны. Свойства ромба АВ

Слайд 13Квадратом называется прямоугольник , у которого все стороны равны.Основные свойства квадрата:

Слайд 14аДве точки и

Слайд 15Фигура называется симметричной относительно прямой а, если для каждой точки фигуры

Слайд 16Две точки и называются симметричными относительно

Слайд 17Фигура называется симметричной относительно точки О, если для каждой точки фигуры

Слайд 18 Людям часто приходилось делить землю по берегам Нила

Слайд 19 Понятие площади. Свойства площадей.Площадь – положительное число, которое показывает сколько

Слайд 20 Единицы измерения площадей.гектарарсотка

Слайд 21 Понятие площади. Свойства площадей.Свойства площадей.1. Равные фигуры имеют равные площади.2.

Слайд 22 Понятие площади. Свойства площадей.3. Площадь квадрата равна квадрату его стороны.

Слайд 23Площадь прямоугольника. Теорема. Площадь прямоугольника равна произведению смежных сторон.АВСD

Слайд 24 Площадь параллелограмма.Теорема. Площадь параллелограмма равна произведению стороны на высоту, проведенную

Слайд 25 Площадь треугольника.Теорема. Площадь треугольника равна половине произведения стороны на высоту,

Слайд 26 Площадь треугольника. Прямоугольный треугольник.аbПлощадь прямоугольного треугольника равна половине произведения его

Слайд 27 Площадь трапеции.Теорема. Площадь трапеции равна произведению полусуммы ее оснований на

Слайд 28В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.c²=a²+b²С – гипотенузаa,b

Слайд 29Определение подобных треугольников Два треугольника называются подобными, если их углы соответственно равны

Слайд 30ABCA1B1C1Если два угла одного треугольника соответственно равны двум углам другого, то

Слайд 31Второй признак подобия треугольниковACA1C1B1BЕсли две стороны одного треугольника пропорциональны двум сторонам

Слайд 32Третий признак подобия треугольниковACBA1C1B1Если три стороны одного треугольника пропорциональны трем сторонам

Слайд 33Средней линией треугольника называется отрезок, соединяющий середины двух его сторон .АВСМNAM=MC