А.С. Пушкин
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
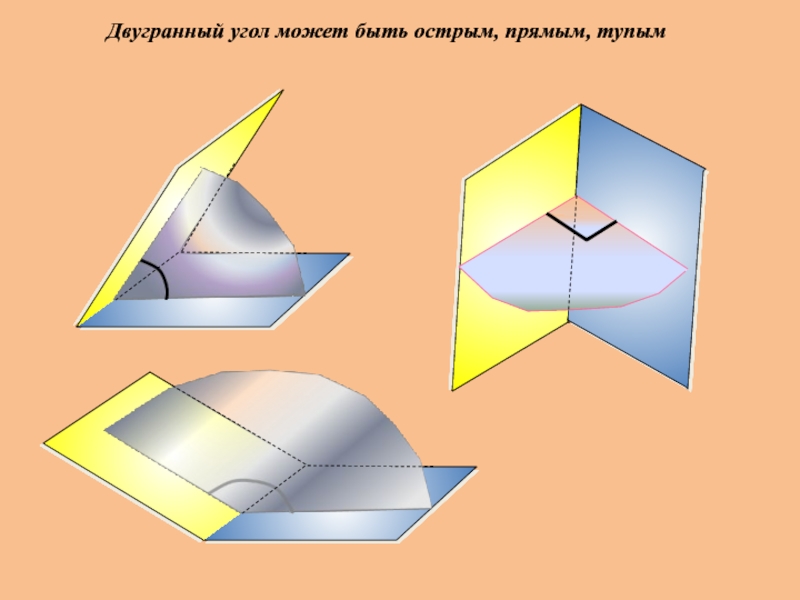
Двугранный угол презентация
Содержание
- 2. Вдохновение есть расположение души к живейшему принятию
- 3. геометрия
- 4. угол
- 5. двугранный
- 7. знакомство с понятиями двугранный угол и его
- 8. Планиметрия Стереометрия Углом на плоскости называется
- 10. Угол
- 11. Угол РОК –
- 12. Все линейные углы двугранного угла
- 15. Построить линейный угол двугранного угла ВАСК.
- 16. Построить линейный угол двугранного угла ВАСК.
- 17. Построить линейный угол двугранного угла ВАСК.
- 18. Построить линейный угол
- 19. Построить линейный угол двугранного угла
- 20. Построить линейный угол двугранного угла ВDСК.
- 21. Построить
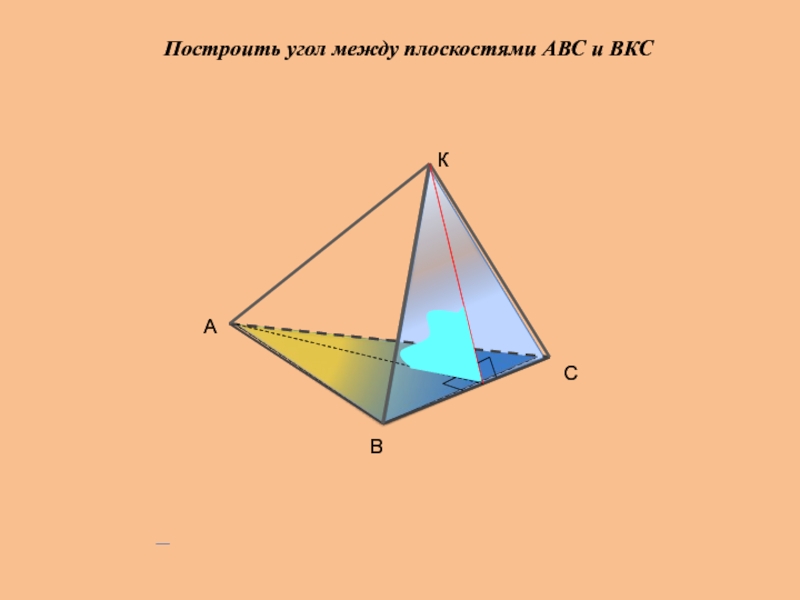
- 22. Построить угол между плоскостями АВС и ВКС
- 23. А1 В1 С1 Д1
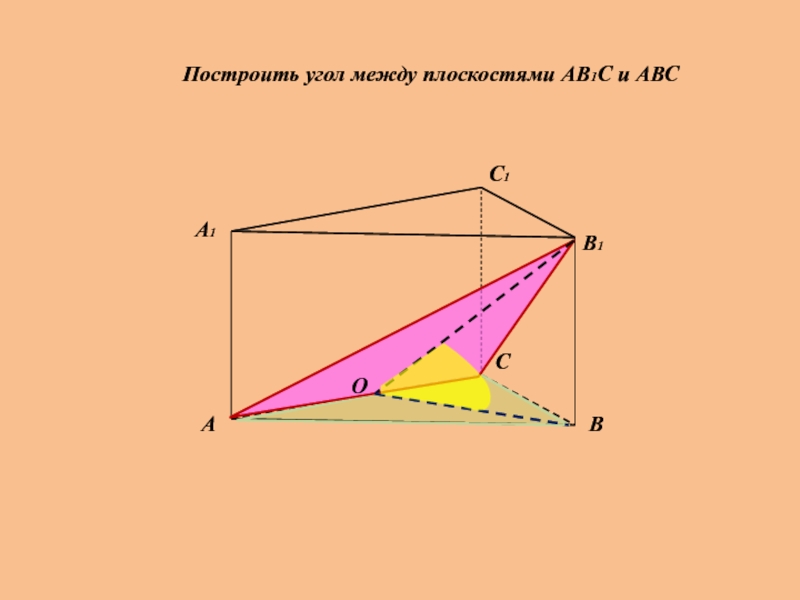
- 24. Построить угол между плоскостями АВ1С и АВС
- 25. А А1 В В1 С С1
- 26. Задача 1: В кубе A…D1
- 27. Задача 1: Ответ: 90o.
- 28. Задача 3: А В С
- 29. Задача 5: Решение: О
- 30. M N А
- 31. Какие знания и умения необходимы при построении
- 33. Интернет – ресурсы http://le-savchen.ucoz.ru/load/3-1-0-168 http://www.uchportal.ru/load/24-1-0-22870 http://nsportal.ru/shkola/geometriya/library/dvugrannyi-ugol
Вдохновение есть расположение души к живейшему принятию впечатлений и соображению понятий, следственно, и объяснению оных. Вдохновение нужно в геометрии, как и в поэзии. А.С. Пушкин
Слайд 2Вдохновение есть расположение души к живейшему принятию впечатлений и соображению понятий,
следственно, и объяснению оных. Вдохновение нужно в геометрии, как и в поэзии.
Слайд 7знакомство с понятиями двугранный угол и его линейный угол, обучение построению
линейного угла данного двугранного угла, развитие навыков построения перпендикуляра к плоскости, применения ТТП, внимания,
воспитание усидчивости, взаимоуважения.
воспитание усидчивости, взаимоуважения.
получить необходимую информацию;
проанализировать полученную информацию;
применить теорию на практике;
заполнить кластер;
оценить свою деятельность.
Слайд 8
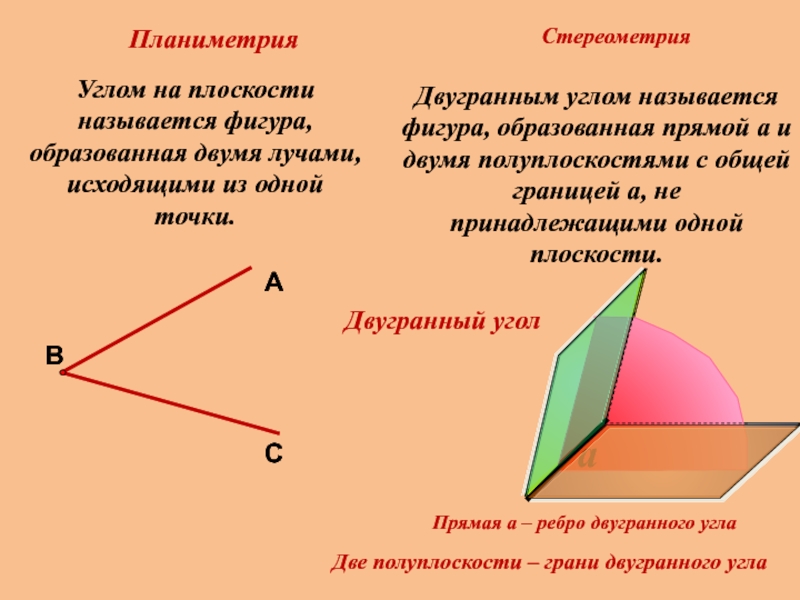
Планиметрия
Стереометрия
Углом на плоскости называется фигура, образованная двумя лучами, исходящими из одной
точки.
Двугранный угол
Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости.
а
Прямая a – ребро двугранного угла
Две полуплоскости – грани двугранного угла
Слайд 10
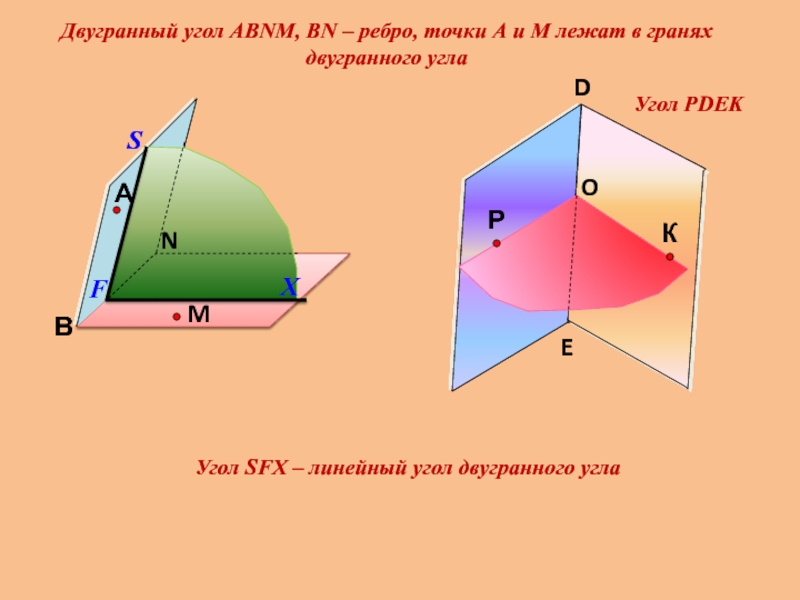
Угол РDEK
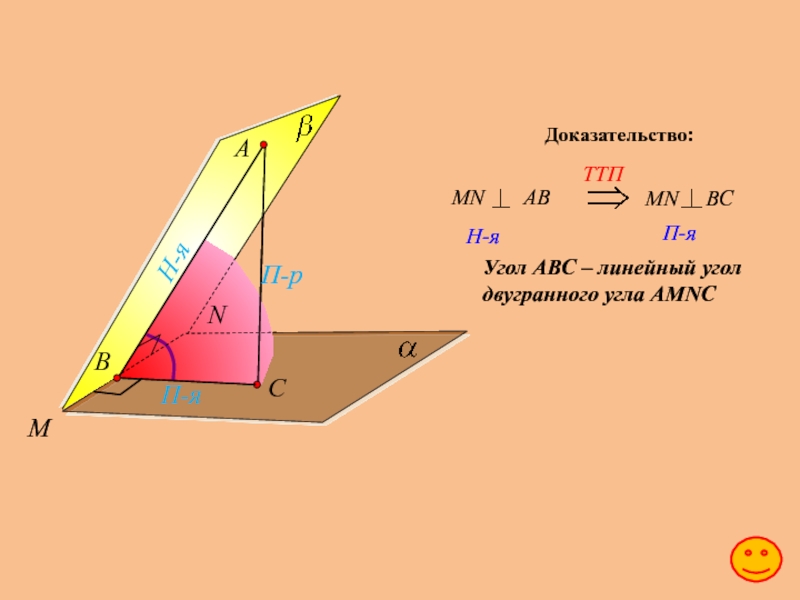
Двугранный угол АВNМ, ВN – ребро, точки А и
М лежат в гранях двугранного угла
А
В
N
Р
M
К
D
E
Угол SFX – линейный угол двугранного угла
Слайд 11
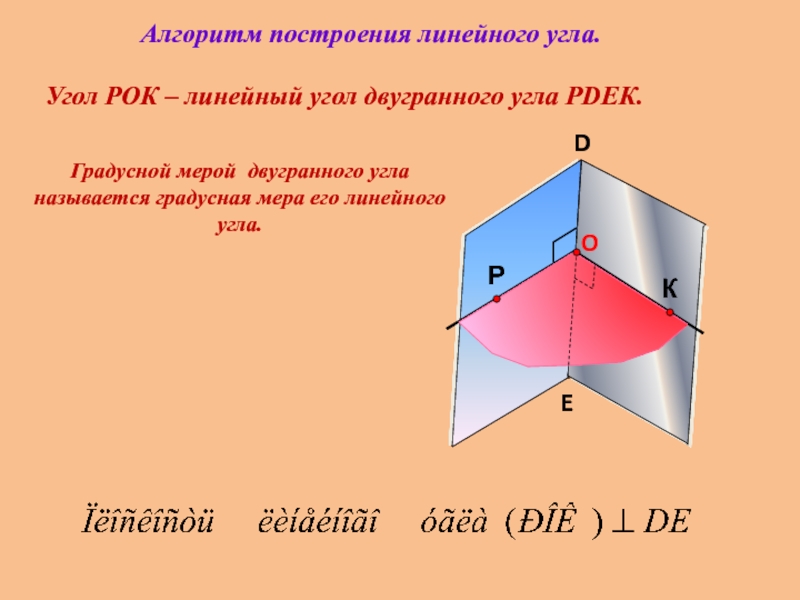
Угол РОК – линейный угол двугранного угла РDEК.
D
E
Градусной мерой двугранного угла
называется градусная мера его линейного угла.
Алгоритм построения линейного угла.
Слайд 12
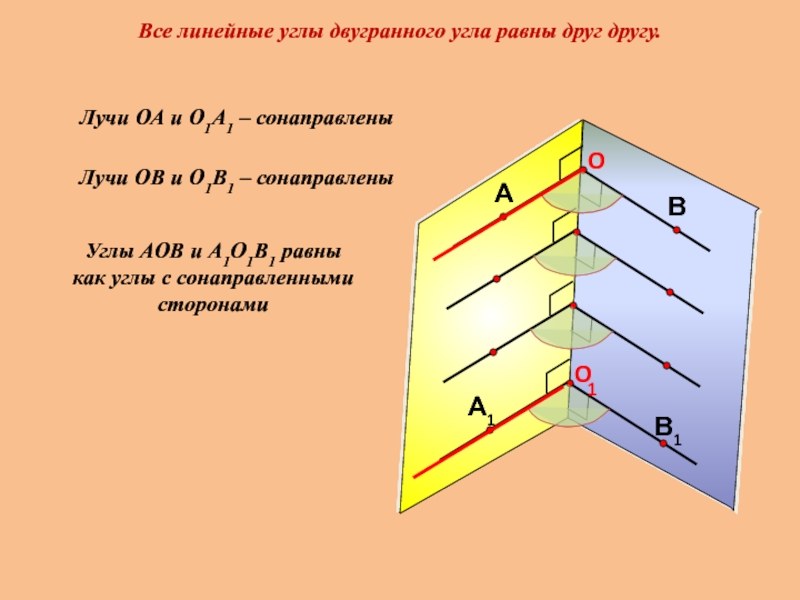
Все линейные углы двугранного угла равны друг другу.
1
Лучи ОА и О1А1
– сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы АОВ и А1О1В1 равны
как углы с сонаправленными сторонами
Слайд 15
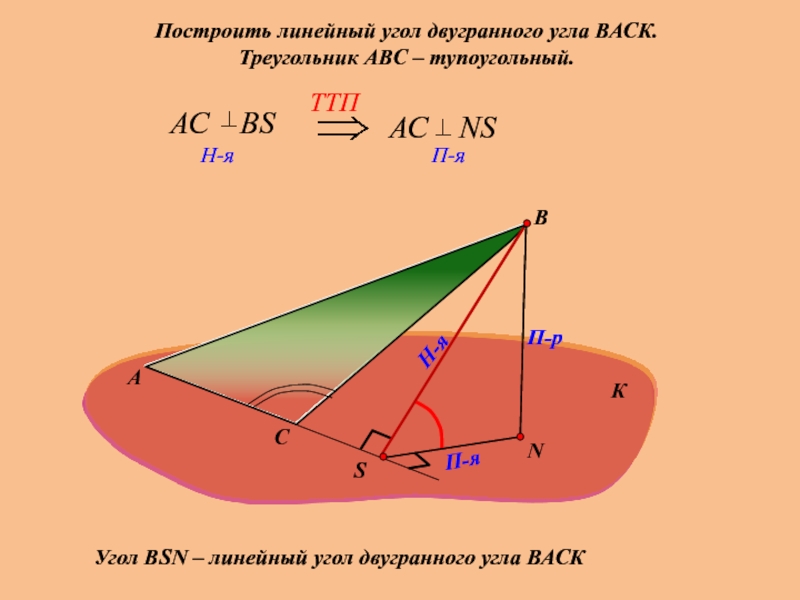
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
А
В
П-р
Н-я
П-я
Угол ВSN –
линейный угол двугранного угла ВАСК
К
С
Слайд 16
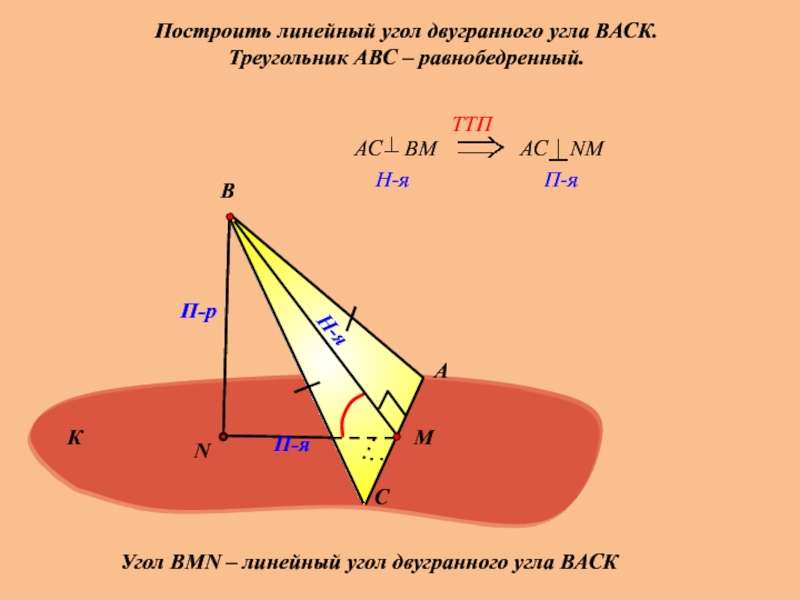
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
А
С
В
П-р
Н-я
П-я
Угол ВMN –
линейный угол двугранного угла ВАСК
К
Слайд 17
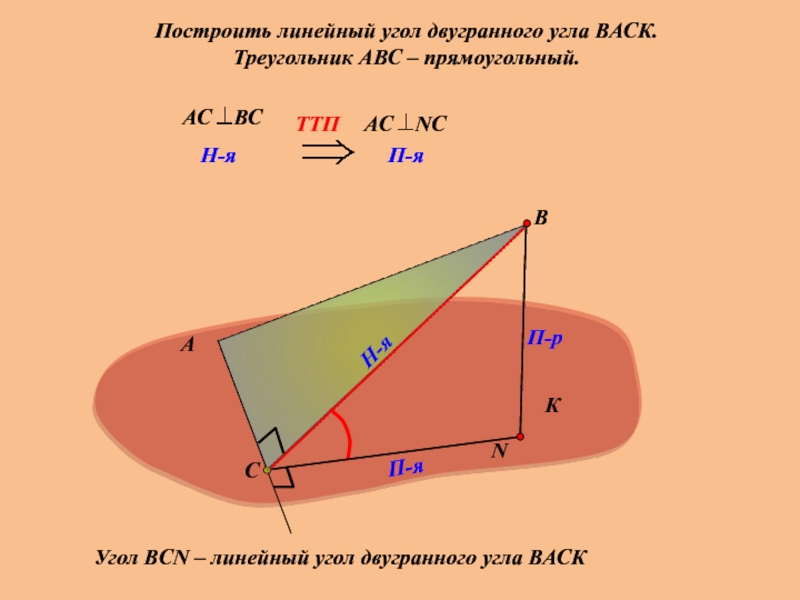
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
А
В
П-р
Н-я
П-я
Угол ВСN –
линейный угол двугранного угла ВАСК
К
С
Слайд 18
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С тупой.
А
В
П-р
П-я
Угол
ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
Слайд 19
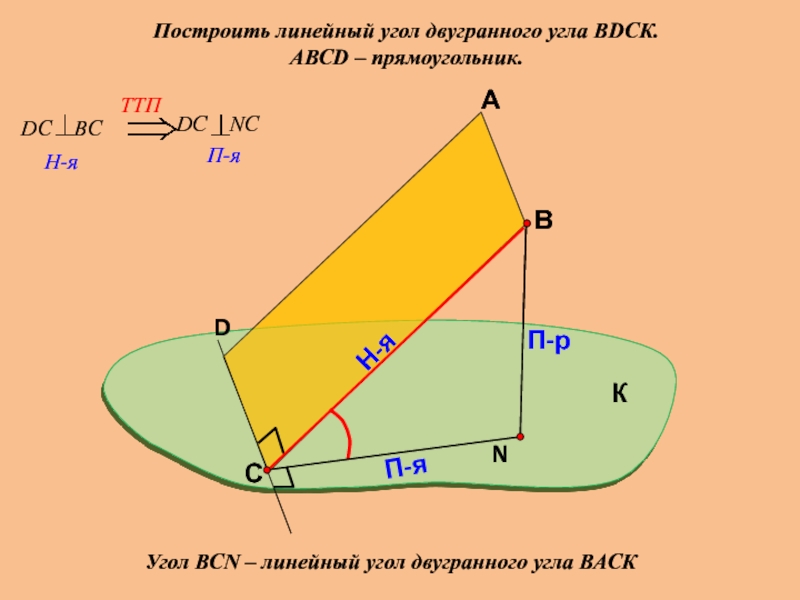
Построить линейный угол двугранного угла ВDСК.
АВСD – прямоугольник.
А
В
П-р
Н-я
П-я
Угол ВСN – линейный
угол двугранного угла ВАСК
К
С
D
Слайд 20
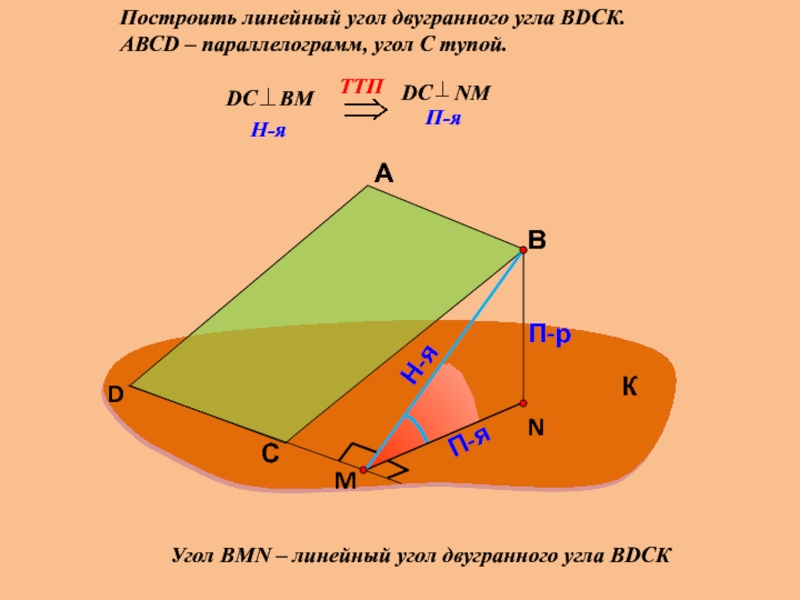
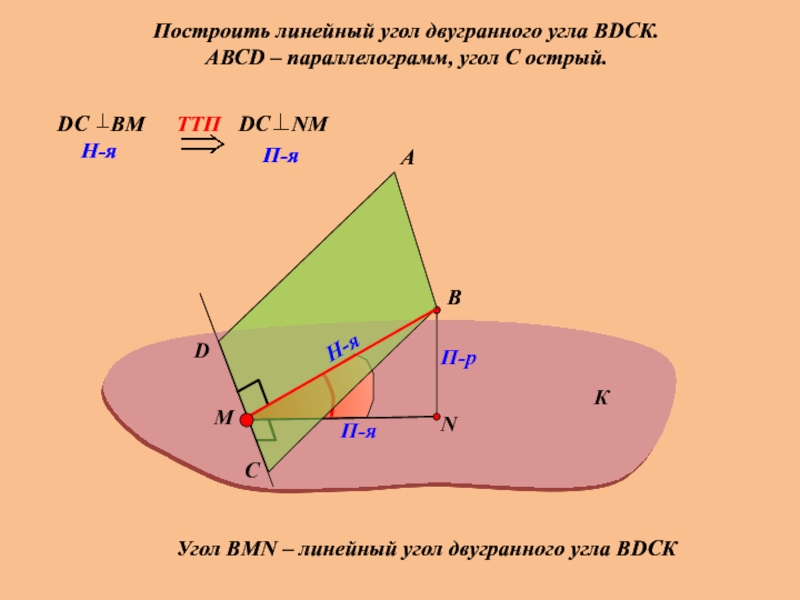
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С острый.
А
В
П-р
П-я
Угол
ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
Слайд 21
Построить линейный угол двугранного угла ВDСК.
АВСD – трапеция, угол С острый.
А
В
П-р
П-я
Угол
ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
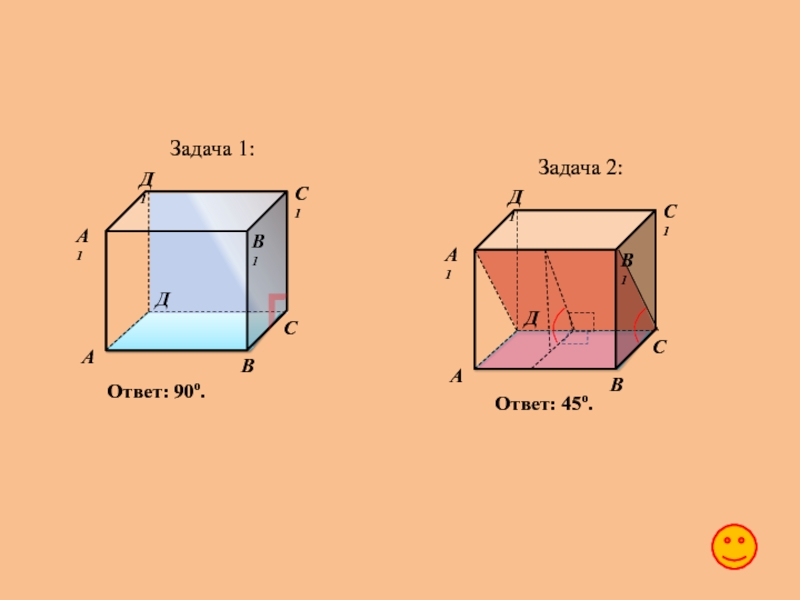
Слайд 26Задача 1:
В кубе A…D1 найдите угол между плоскостями ABC
и CDD1.
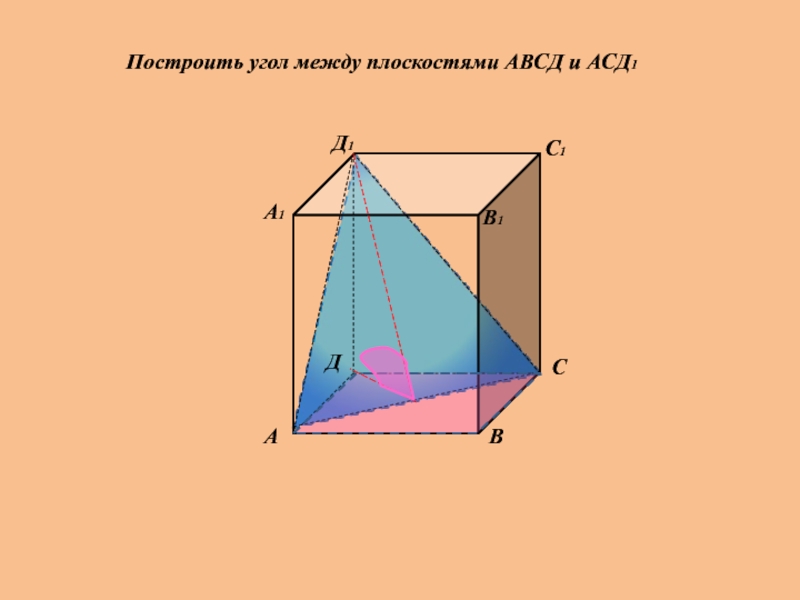
В кубе A…D1 найдите угол между плоскостями ABC и CDA1.
Задача 2:
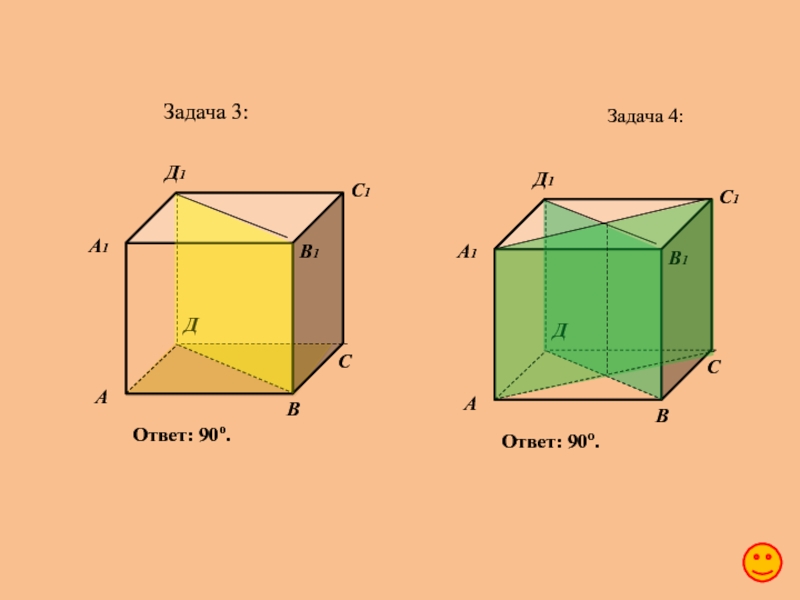
Задача 3:
В кубе A…D1 найдите угол между плоскостями ABC и BDD1.
Задача 4:
В кубе A…D1 найдите угол между плоскостями ACC1 и BDD1.
В кубе A…D1 найдите угол между плоскостями BC1D и BA1D.
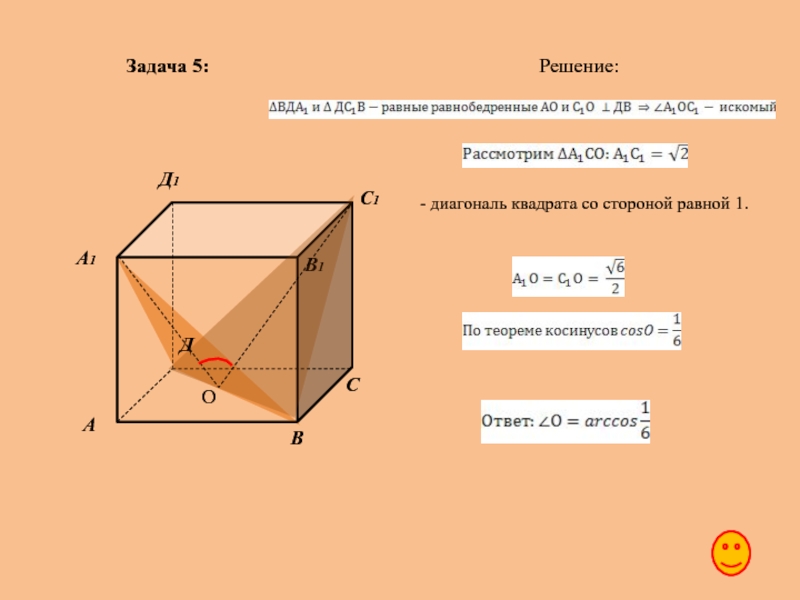
Задача 5:
Задача 6:
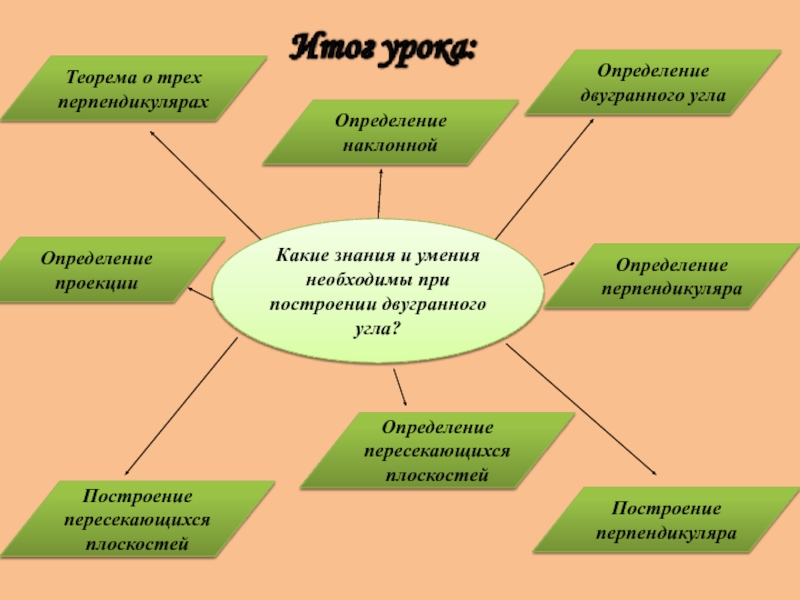
Слайд 31Какие знания и умения необходимы при построении двугранного угла?
Определение двугранного угла
Теорема
о трех перпендикулярах
Построение перпендикуляра
Определение пересекающихся плоскостей
Построение пересекающихся плоскостей
Определение перпендикуляра
Определение наклонной
Определение проекции
Слайд 33 Интернет – ресурсы
http://le-savchen.ucoz.ru/load/3-1-0-168
http://www.uchportal.ru/load/24-1-0-22870
http://nsportal.ru/shkola/geometriya/library/dvugrannyi-ugol
