- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Конечные разности. Первая и вторая интерполяционные формулы Ньютона. Погрешности интерполяции. (Лекция 4) презентация
Содержание
- 1. Конечные разности. Первая и вторая интерполяционные формулы Ньютона. Погрешности интерполяции. (Лекция 4)
- 2. Конечные разности 1–го порядка Если интерполируемая функция
- 3. Конечные разности высших порядков Используя конечные разности
- 4. Таблица конечных разностей
- 5. Конечные разности и степень многочлена По величине
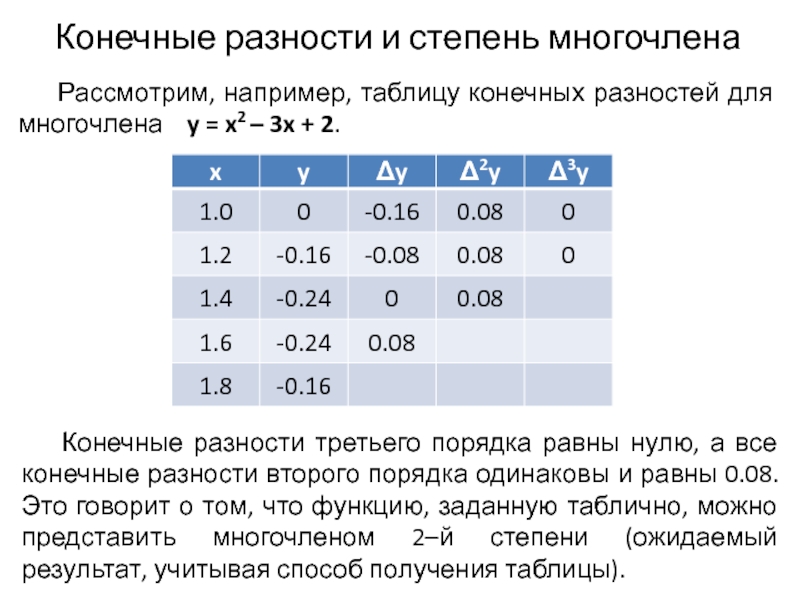
- 6. Конечные разности и степень многочлена Рассмотрим, например,
- 7. Первая интерполяционная формула Ньютона
- 8. Первая интерполяционная формула Ньютона
- 9. Первая интерполяционная формула Ньютона
- 10. Первая интерполяционная формула Ньютона
- 11. Пример использования первой интерполяционной формулы Ньютона Пусть
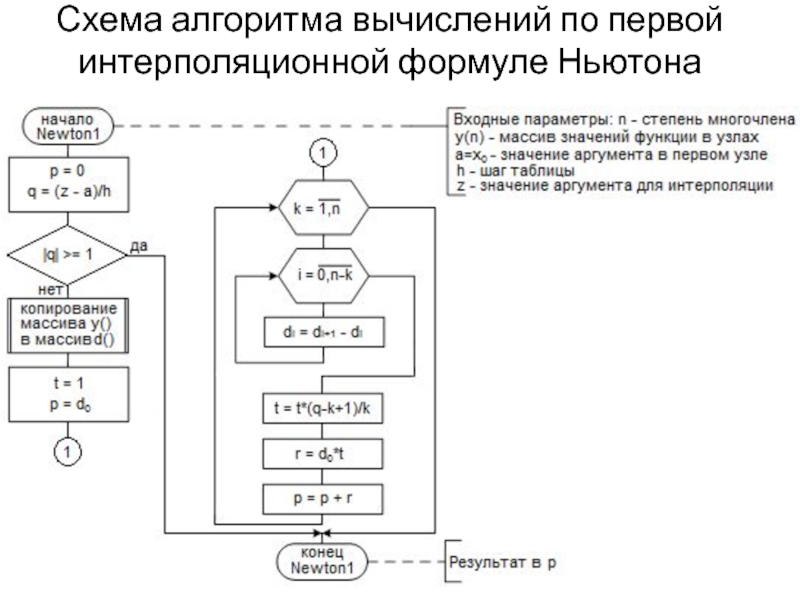
- 12. Схема алгоритма вычислений по первой интерполяционной формуле Ньютона
- 13. Вторая интерполяционная формула Ньютона
- 14. Вторая интерполяционная формула Ньютона
- 15. Вторая интерполяционная формула Ньютона
- 16. Пример использования второй интерполяционной формулы Ньютона Пусть
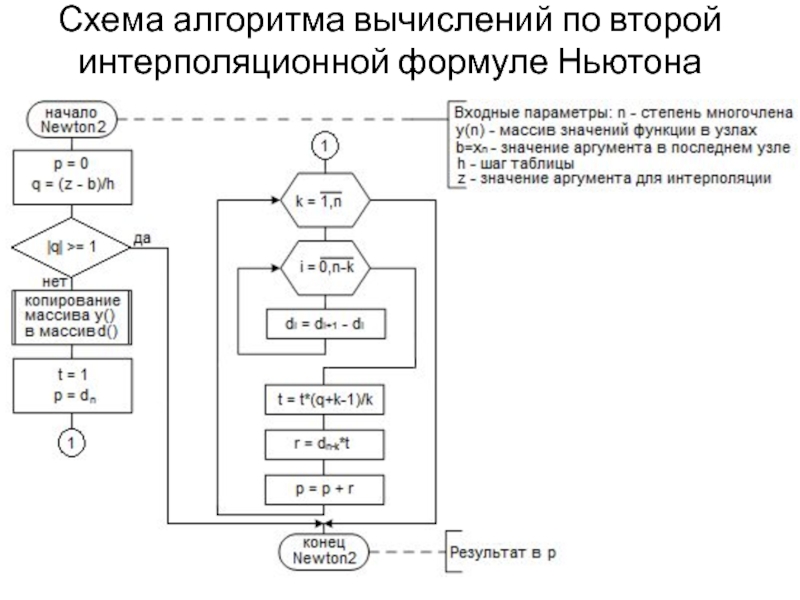
- 17. Схема алгоритма вычислений по второй интерполяционной формуле Ньютона
- 18. Погрешности интерполяции Интерполирующая функция в точках между
- 19. Погрешности интерполяции Тогда
- 20. Выбор узлов интерполяции по формуле Лагранжа При
- 21. Практическая оценка погрешности интерполяции по формуле Лагранжа
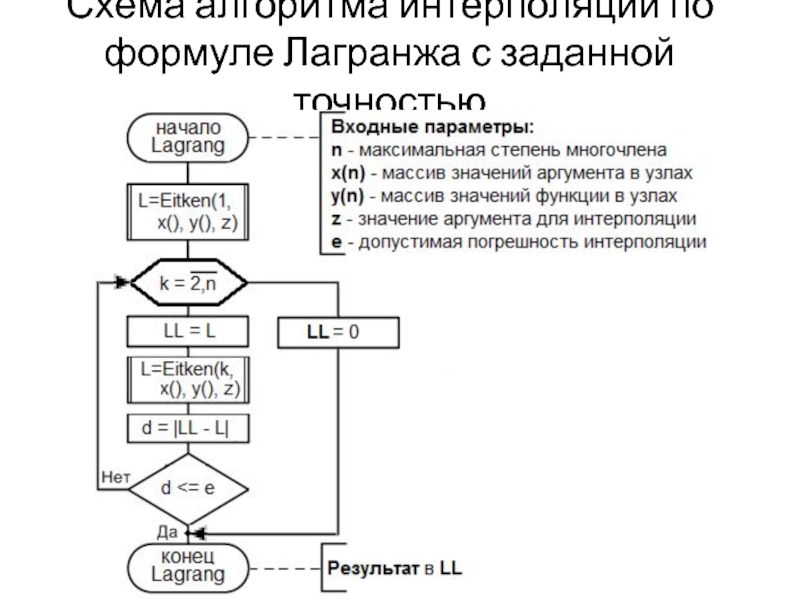
- 22. Схема алгоритма интерполяции по формуле Лагранжа с заданной точностью
- 23. Оценка погрешностей интерполяционных формул Ньютона
- 24. Практическая оценка погрешностей интерполяционных формул Ньютона
- 25. Интерполяция по формулам Ньютона с заданной точностью
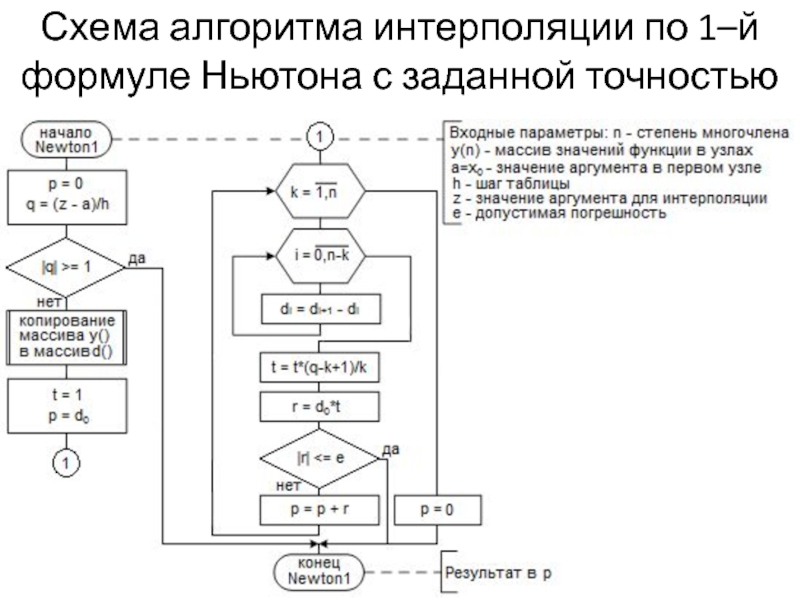
- 26. Схема алгоритма интерполяции по 1–й формуле Ньютона с заданной точностью
Слайд 1Лекция 4
Конечные разности
Первая интерполяционная формула Ньютона
Вторая интерполяционная формула Ньютона
Погрешности интерполяции
Слайд 2Конечные разности 1–го порядка
Если интерполируемая функция y = f(x) задана в
Конечной разностью первого порядка называется разность Δyi = yi+1 - yi, где yi+1= f(xi+h) и yi = f(xi). Для функции, заданной таблично в (n+1) узлах, i = 0, 1, 2, …, n, конечные разности первого порядка могут быть вычислены в точках 0, 1, 2,…, n - 1:
Слайд 3Конечные разности высших порядков
Используя конечные разности первого порядка, можно получить конечные
Конечные разности k-го порядка в узле с номером i могут быть вычислены через разности (k-1)–го порядка:
Любые конечные разности можно вычислить через значения функции в узлах интерполяции, например:
Слайд 5Конечные разности и степень многочлена
По величине конечных разностей можно сделать вывод
Слайд 6Конечные разности и степень многочлена
Рассмотрим, например, таблицу конечных разностей для многочлена
Конечные разности третьего порядка равны нулю, а все конечные разности второго порядка одинаковы и равны 0.08. Это говорит о том, что функцию, заданную таблично, можно представить многочленом 2–й степени (ожидаемый результат, учитывая способ получения таблицы).
Слайд 11Пример использования первой интерполяционной формулы Ньютона
Пусть интерполируемая функция f(x) задана той
Шаг таблицы h = 0.2
q = (x – x0)/h = 0.5
Результат совпадает с значением многочлена y = x2 – 3x + 2, из которого получена таблица
Слайд 16Пример использования второй интерполяционной формулы Ньютона
Пусть интерполируемая функция f(x) задана той
Шаг таблицы h = 0.2
q = (x – xn)/h = -0.5
Результат совпадает с значением многочлена y = x2 – 3x + 2, из которого получена таблица
Слайд 18Погрешности интерполяции
Интерполирующая функция в точках между узлами интерполяции заменяет интерполирующую функцию
f(x) = F(x) + R(x), где R(x) – погрешность интерполяции.
Для оценки погрешности необходимо иметь необходимо иметь определенную информацию об интерполируемой функции f(x). Предположим, что f(x) определена на отрезке [a;b], содержащем все узлы xi, и при x, принадлежащем [a;b], имеет все производные f'(x), f''(x), … f(n+1)(x) до (n+1)–го порядка включительно.
Слайд 20Выбор узлов интерполяции по формуле Лагранжа
При фиксированной степени многочлена:
При последовательном увеличении
x
x0
x1
x2
x3
x4
x5
x*
x
x4
x2
x0
x1
x3
x5
x*
Слайд 25Интерполяция по формулам Ньютона с заданной точностью
Сравнивая эти формулы с формулами
Если задана допустимая погрешность интерполяции ε, то надо последовательно добавлять новые узлы и, соответственно, новые слагаемые, увеличивая степень интерполяционного многочлена до тех пор, пока очередное слагаемое не станет меньше ε.