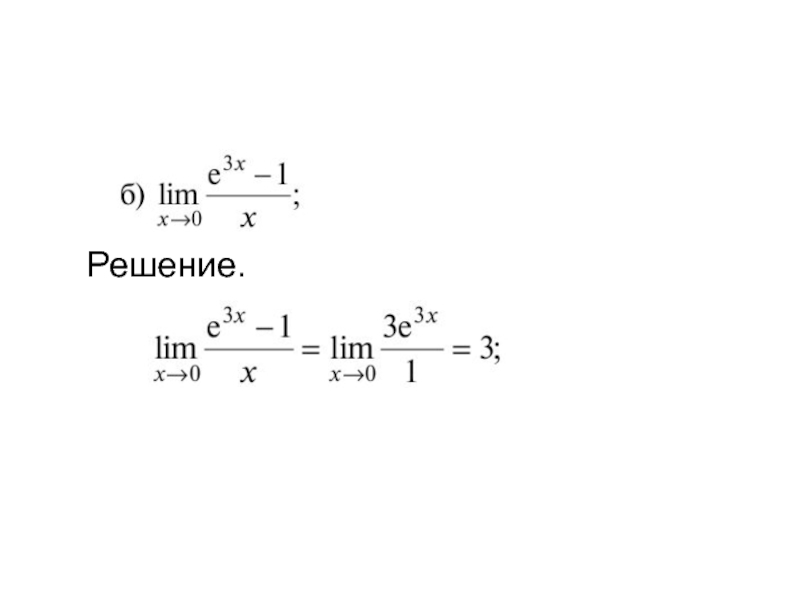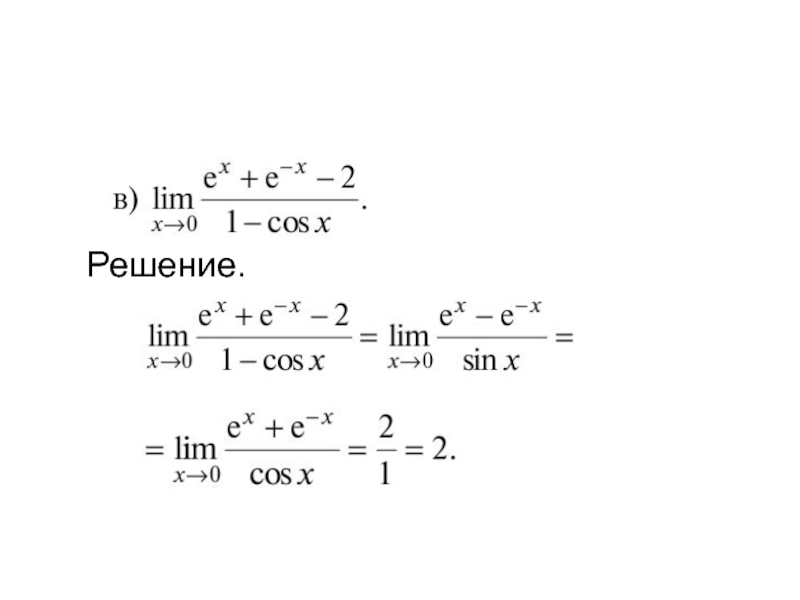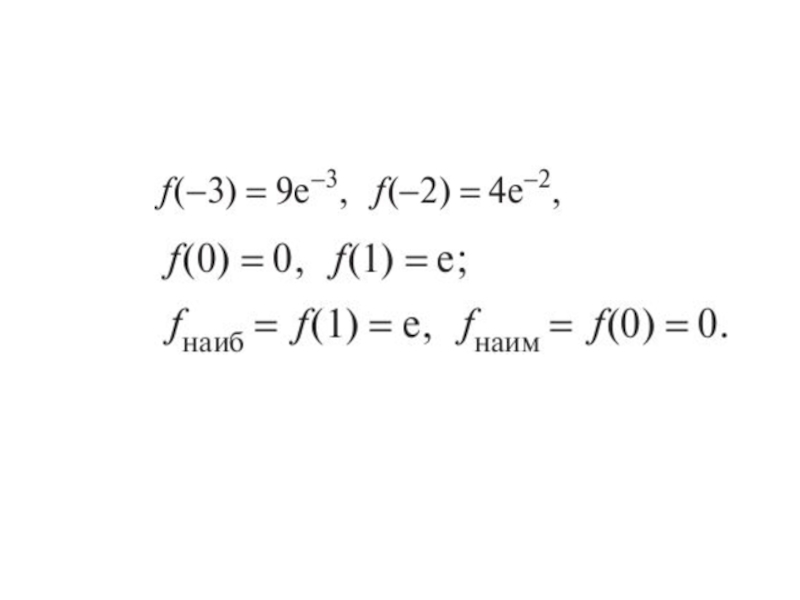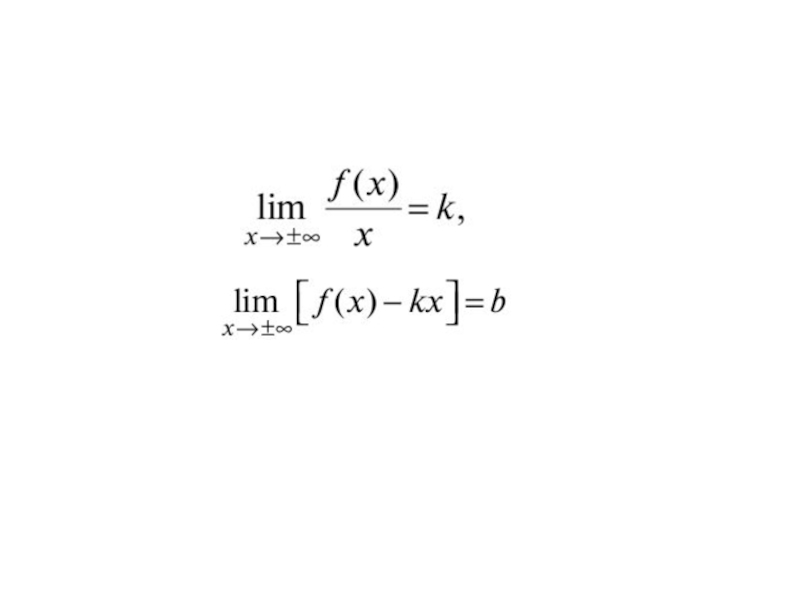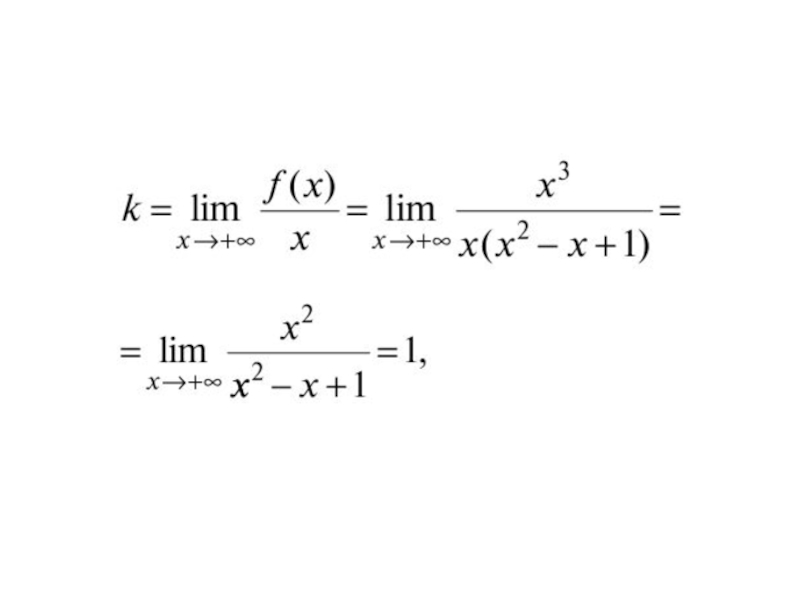- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исследование функций с помощью производной презентация
Содержание
- 1. Исследование функций с помощью производной
- 2. Правило Лопиталя Рассмотрим отношение
- 3. Если существует
- 4. Неопределенность вида
- 5. Пример. Вычислить пределы: Решение.
- 6. Решение.
- 7. Решение.
- 8. Точка
- 9. Общий термин
- 10. Точки, в
- 11. Первое достаточное условие экстремума
- 12. Исследование функции на экстремум с помощью первой
- 13. Пример. Исследовать функцию
- 14. Исследуем знак производной:
- 16. Наибольшее и наименьшее значения функции на отрезке
- 17. Схема для
- 18. Пример.
- 20. Выпуклость и вогнутость графика функции. Точки перегиба
- 22. Если функция
- 23. Точка, отделяющая
- 24. Достаточным условием перегиба
- 25. Асимптоты Прямая линия
- 26. Различают три вида
- 27. Прямая y=b
- 28. Прямая
- 30. Пример.
- 32. Уравнение наклонной асимптоты:
- 33. Пример. Найти
- 34. Найдем наклонную асимптоту:
Слайд 2Правило Лопиталя
Рассмотрим отношение двух функций
Будем говорить, что это отношение при есть неопределенность вида
если
если
Слайд 3
Если существует
то вычисление этого предела называют раскрытием упомянутой неопределенности.
Слайд 4Неопределенность вида
В случае когда функции
стремятся к бесконечности при , также применимо правило Лопиталя.
Справедливо правило Лопиталя и для функций стремящихся к бесконечности при :
Справедливо правило Лопиталя и для функций стремящихся к бесконечности при :
Слайд 8 Точка называется точкой локального
максимума функции f(x), если в некоторой окрестности точки выполняется неравенство
Точка называется точкой локального минимума функции f(x), если в некоторой окрестности точки выполняется неравенство
Точка называется точкой локального минимума функции f(x), если в некоторой окрестности точки выполняется неравенство
Экстремум функции
Слайд 9
Общий термин для локального максимума и локального
минимума – локальный экстремум.
Необходимое условие экстремума дифференцируемой функции: для того чтобы дифференцируемая функция f(x) имела в точке локальный экстремум, необходимо, чтобы в этой точке выполнялось равенство
Необходимое условие экстремума дифференцируемой функции: для того чтобы дифференцируемая функция f(x) имела в точке локальный экстремум, необходимо, чтобы в этой точке выполнялось равенство
Слайд 10
Точки, в которых производная функции обращается в
нуль или не существует, называются критическими (или стационарными).
Слайд 11Первое достаточное условие экстремума
Пусть функция f(x) непрерывна
в некотором интервале, содержащем критическую точку, и дифференцируема во всех точках этого интервала, кроме, может быть, самой точки . Если при переходе через точку производная меняет знак с «плюса» на «минус», то в точке имеется локальный максимум, а если с «минуса» на «плюс», то минимум.
Слайд 12Исследование функции на экстремум с помощью первой производной
1.
Найти производную
2. Найти критические точки.
3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии локальных экстремумов функции.
4. Найти значения функции в точках локального экстремума.
2. Найти критические точки.
3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии локальных экстремумов функции.
4. Найти значения функции в точках локального экстремума.
Слайд 16Наибольшее и наименьшее значения функции на отрезке
Наибольшее
или наименьшее значение функции может достигаться как в точках локального экстремума, так и на концах отрезка.
Слайд 17
Схема для нахождения наибольшего и наименьшего значений
функции на отрезке:
1. Найти производную
2. Найти критические точки.
3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее и наименьшее.
1. Найти производную
2. Найти критические точки.
3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее и наименьшее.
Слайд 18
Пример.
Найти наибольшее
и наименьшее значения функции
на отрезке [ -3, 1].
Решение.
Стационарные точки:
на отрезке [ -3, 1].
Решение.
Стационарные точки:
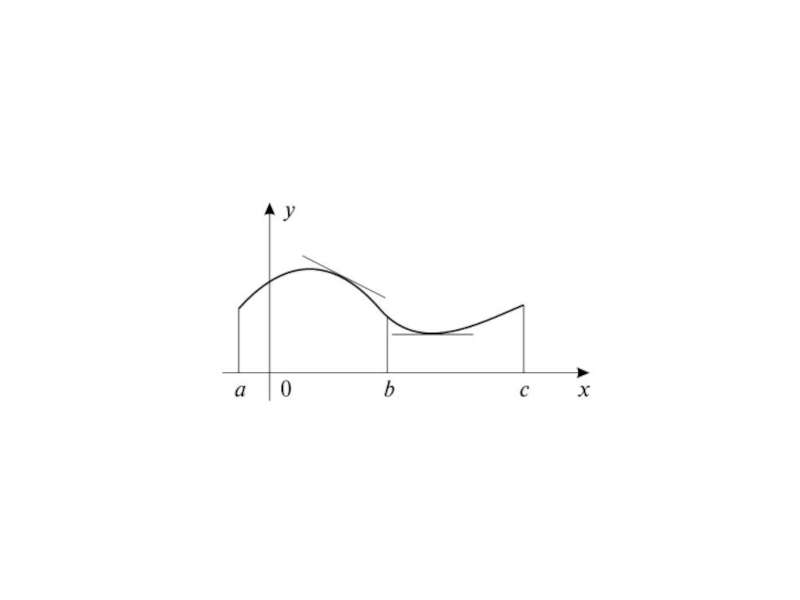
Слайд 20Выпуклость и вогнутость графика функции. Точки перегиба
Кривая
y=f(x) имеет на (a; b) выпуклость, направленную вверх, если все точки кривой лежат ниже любой ее касательной на этом интервале.
Кривая y=f(x) имеет на (b; c) выпуклость, направленную вниз, если все точки кривой лежат выше любой ее касательной на этом интервале.
Кривая y=f(x) имеет на (b; c) выпуклость, направленную вниз, если все точки кривой лежат выше любой ее касательной на этом интервале.
Слайд 22
Если функция y= f(x) имеет на интервале
(a; b) вторую производную и
на (a; b), то график этой функции имеет на (a; b) выпуклость, направленную вниз; если же ,
на (a; b), то график имеет на (a, b) выпуклость, направленную вверх.
на (a; b), то график этой функции имеет на (a; b) выпуклость, направленную вниз; если же ,
на (a; b), то график имеет на (a, b) выпуклость, направленную вверх.
Слайд 23
Точка, отделяющая выпуклую часть кривой от вогнутой,
называется точкой перегиба.
Необходимое условие перегиба в точке для графика функции f(x), имеющей в этой точке непрерывную вторую производную, заключается в том, что
Необходимое условие перегиба в точке для графика функции f(x), имеющей в этой точке непрерывную вторую производную, заключается в том, что
Слайд 24
Достаточным условием перегиба является смена знака второй производной
функции y=f(x) при переходе через точку (т.е.если вторая производная имеет разные знаки слева и справа от , то график функции имеет перегиб при
Слайд 25Асимптоты
Прямая линия называется асимптотой графика функции y
= f(x), если расстояние от точки M, лежащей на графике, до этой прямой стремится к нулю при неограниченном удалении точки M от начала координат.
Слайд 26
Различают три вида асимптот: вертикальные, горизонтальные и наклонные
.
Прямая x=a называется вертикальной асимптотой графика
функции y=f(x), если хотя бы одно из предельных значений или
равно или
Прямая x=a называется вертикальной асимптотой графика
функции y=f(x), если хотя бы одно из предельных значений или
равно или
Слайд 28
Прямая
называется наклонной асимптотой графика функции y=f(x) при
если f(x) можно представить в виде
где при
если f(x) можно представить в виде
где при
Слайд 30
Пример.
Найти наклонную асимптоту
графика функции
Решение.
Уравнение наклонной асимптоты имеет вид:
Решение.
Уравнение наклонной асимптоты имеет вид:
Слайд 33
Пример.
Найти асимптоты графика функции
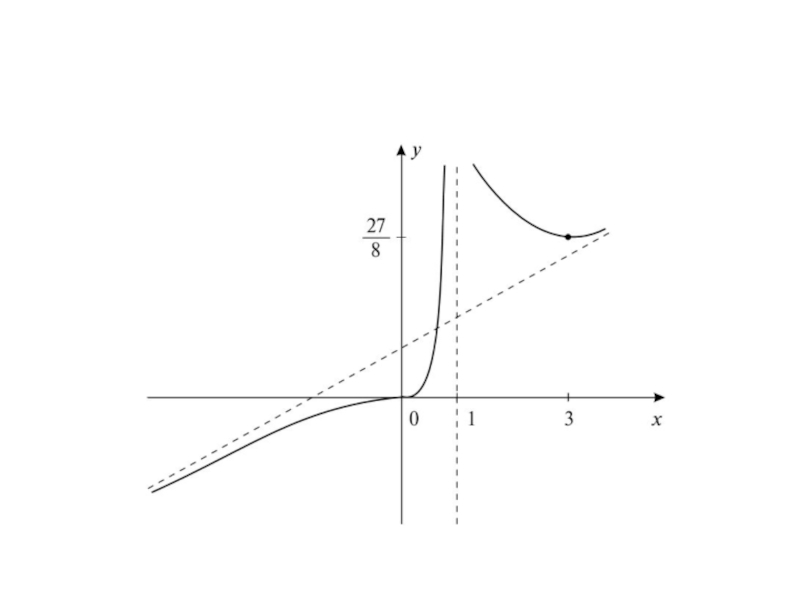
Решение.
x = 1 – вертикальная асимптота.
Горизонтальных асимптот нет.
Горизонтальных асимптот нет.