- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проверка гипотез презентация
Содержание
- 1. Проверка гипотез
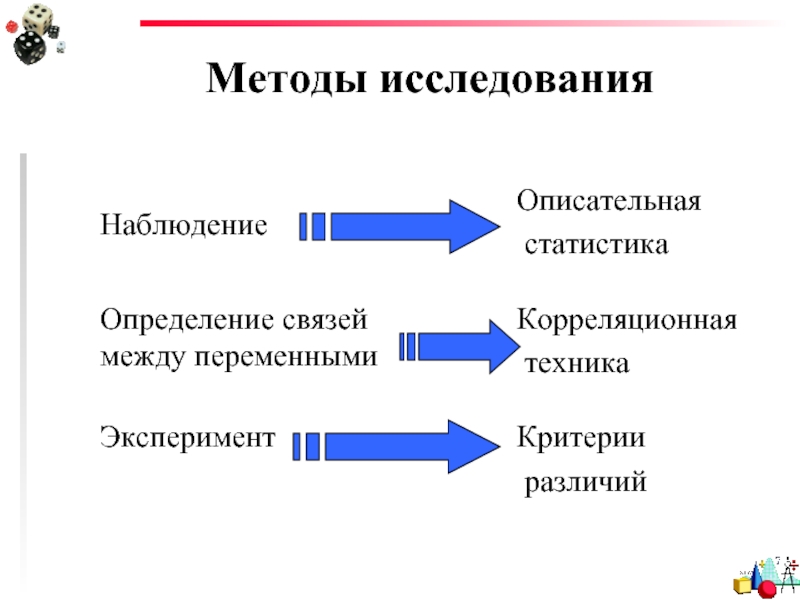
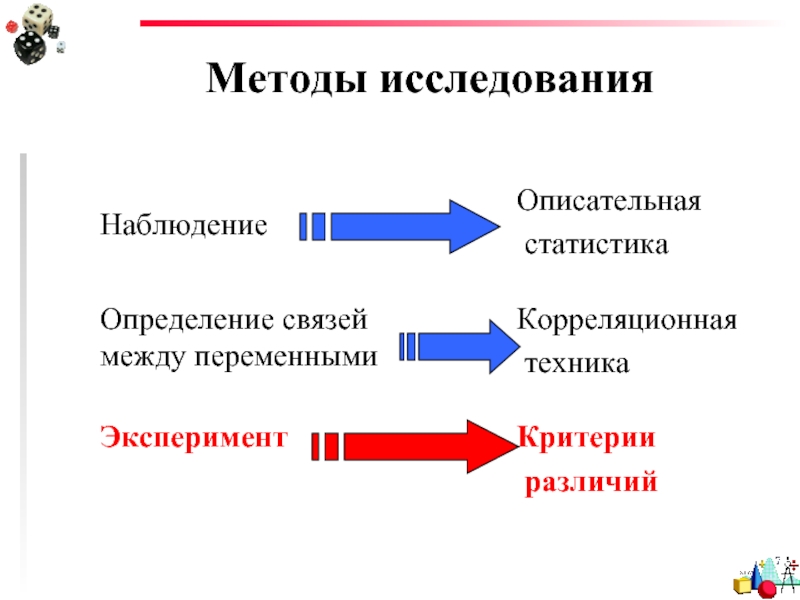
- 2. Методы исследования
- 3. Методы исследования
- 4. Цели Основы эксперимента Логика проверки гипотез Простейшие критерии для проверки гипотез
- 5. Эксперимент Как найти причину? А
- 6. Эксперимент Как найти причину? А
- 7. Логика проверки гипотез Чем реже или необычнее
- 8. Логика проверки гипотез В социальных
- 9. Логика проверки гипотез 1) Если некоторое событие
- 10. Логика проверки гипотез Уровень статистической значимости, установленный
- 11. Логика проверки гипотез Чтобы определить, стоит ли
- 12. Логика проверки гипотез
- 13. Гипотезы Нуль-гипотеза - это гипотеза об отсутствии
- 14. Гипотезы Альтернативная гипотеза (гипотеза исследования, экспериментальная гипотеза,
- 15. Гипотезы Нуль-гипотеза никогда не может быть доказана!
- 16. Гипотезы Когда нуль-гипотеза может быть
- 17. Гипотезы Уровень статистической значимости р представляет собой, таким образом, вероятность неправильного отвержения нуль-гипотезы.
- 18. Альтернативные гипотезы бывают Направленные PQ Ненаправленные P≠Q
- 19. Проверка гипотез осуществляется с помощью
- 20. Случайная величина – это величина, которая в
- 21. Критическое значение гипотезы - это значение
- 22. Критическая область гипотезы - это совокупность
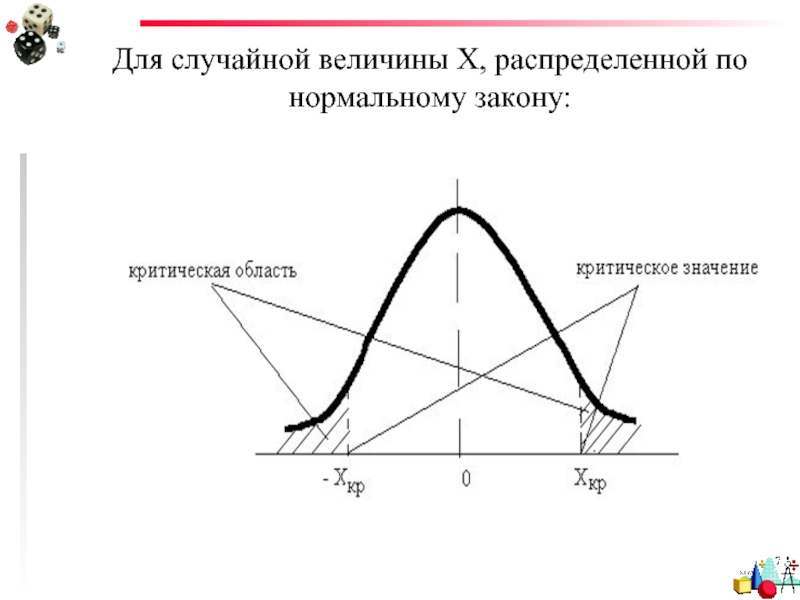
- 23. Для случайной величины Х, распределенной по нормальному закону:
- 24. Направленные гипотезы Для направленных гипотез используется только
- 25. Направленные гипотезы В этом случае уровень статистической
- 26. Ненаправленные гипотезы Для ненаправленных гипотез используется вся критическая область
- 27. Ненаправленные гипотезы В этом случае уровень статистической
- 28. Ошибки I и II рода
- 29. Ошибка первого рода Ошибка, состоящая в том,
- 30. Ошибка второго рода Ошибка, состоящая в том,
- 31. Можем ли мы узнать каким-то образом, что совершаем ошибку I или II рода? Увы! НИКАК!
- 32. Цели Основы эксперимента Логика проверки гипотез
- 33. Полезная литература: К практическому занятию по проверке
- 34. СПАСИБО ЗА ВНИМАНИЕ!
Методы исследования
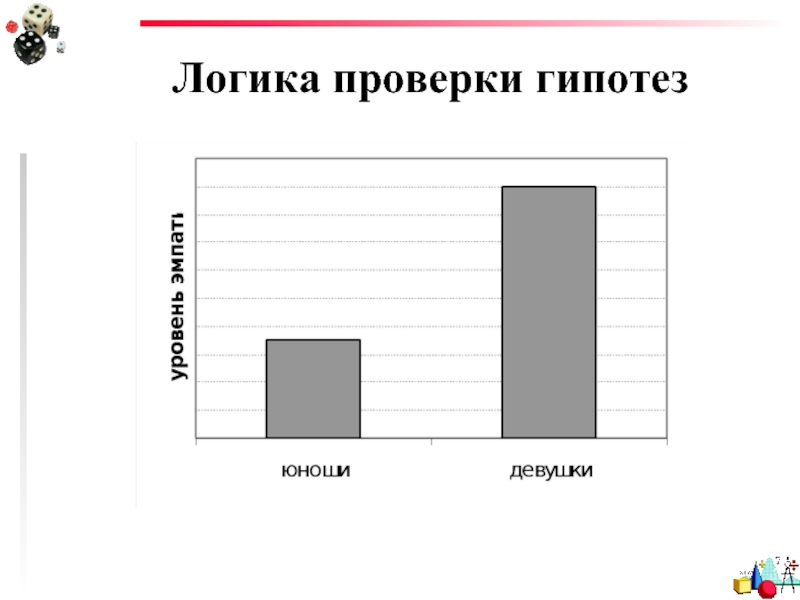
Слайд 7Логика проверки гипотез
Чем реже или необычнее некоторое явление, тем более мы
склонны искать ему объяснение отличное от простой случайности.
Слайд 8Логика проверки гипотез
В социальных науках исследователи согласились, что следующие
два значения будут основанием для допущения действия неслучайного фактора:
Слайд 9Логика проверки гипотез
1) Если некоторое событие происходит случайно в 5% случаев
или еще реже, то предполагается, что это происходит благодаря действию некоторых неслучайных факторов. Это значение называется 5%-м уровнем статистической значимости или уровнем статистической значимости, равным 0,05.
2) Если некоторое событие происходит случайно в 1% случаев или еще реже, то предполагается, что это происходит благодаря действию некоторых неслучайных факторов. Это значение называется 1%-м уровнем статистической значимости или уровнем статистической значимости, равным 0,01.
Слайд 10Логика проверки гипотез
Уровень статистической значимости, установленный исследователями для заключения о действии
неслучайных факторов часто называется уровнем α (или p).
Когда мы говорим о 5% уровне статистической значимости, то р=0,05.
Когда мы говорим об 1% уровне статистической значимости, то р=0,01.
Когда мы говорим о 5% уровне статистической значимости, то р=0,05.
Когда мы говорим об 1% уровне статистической значимости, то р=0,01.
Слайд 11Логика проверки гипотез
Чтобы определить, стоит ли объяснять какое-либо явление действием некоторого
неслучайного фактора, надо найти вероятность того, что это явление произойдет случайно и сравнить с выбранным уровнем статистической значимости.
Слайд 13Гипотезы
Нуль-гипотеза - это гипотеза об отсутствии различий.
Она обычно обозначается H0
и называется нулевой, потому что содержит число 0:
P-Q=0
P-Q=0
Слайд 14Гипотезы
Альтернативная гипотеза (гипотеза исследования, экспериментальная гипотеза, …) - это гипотеза о
значимости различий.
Она обычно обозначается H1.
Она обычно обозначается H1.
Слайд 15Гипотезы
Нуль-гипотеза никогда не может быть доказана!
Альтернативная гипотеза тоже не может быть
доказана прямо!
Но если мы можем отвергнуть нуль-гипотезу, то можем принять альтернативную ей.
Но если мы можем отвергнуть нуль-гипотезу, то можем принять альтернативную ей.
Слайд 16Гипотезы
Когда нуль-гипотеза может быть отвергнута?
Если вы взяли
р=0.05, то вы отвергаете нуль-гипотезу, если данный результат появляется в 5% случаев или реже.
Если вы взяли р=0.01, то вы отвергаете нуль-гипотезу, если данный результат появляется в 1% случаев или реже.
Слайд 17Гипотезы
Уровень статистической значимости р представляет собой, таким образом, вероятность
неправильного отвержения нуль-гипотезы.
Слайд 19
Проверка гипотез
осуществляется с помощью критериев статистической оценки различий
Статистический критерий (критерий)
- это случайная величина, закон распределения которой известен и которая служит для проверки нуль-гипотезы.
Слайд 20Случайная величина – это величина, которая в результате опыта может принимать
то или иное значение, причем неизвестно заранее, какое именно.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значения\ми случайной величины и соответствующими им вероятностями.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значения\ми случайной величины и соответствующими им вероятностями.
Слайд 21 Критическое значение гипотезы - это значение случайной величины, соответствующее ее
уровню значимости и делящее все множество ее значений на две области - критическую и допустимую.
Слайд 22 Критическая область гипотезы - это совокупность значений критерия, при которых
отвергают нуль-гипотезу. Эти значения заключены вне интервала, образованного критическими значениями гипотезы (меньше меньшего и больше большего).
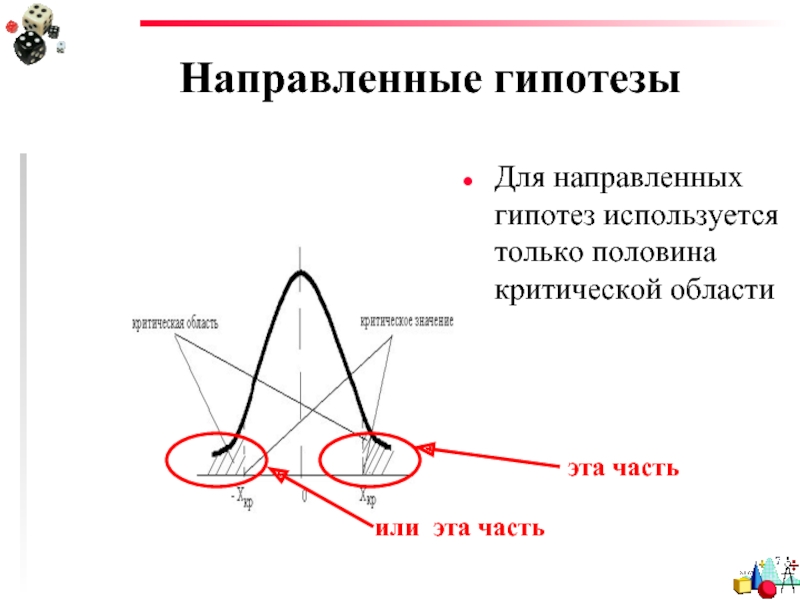
Слайд 24Направленные гипотезы
Для направленных гипотез используется только половина критической области
эта часть
или эта
часть
Слайд 25Направленные гипотезы
В этом случае уровень статистической значимости получается «с одним хвостом»
распределения и называется one-tailed probability value (p value)
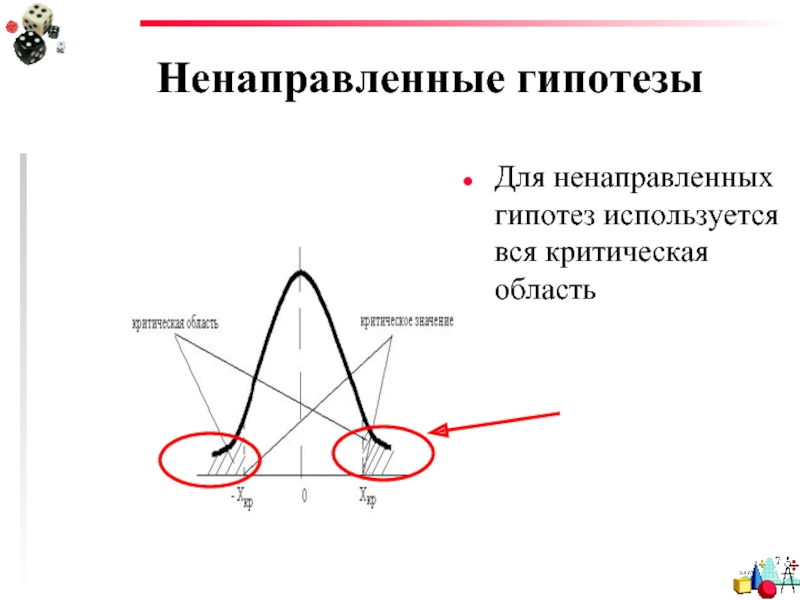
Слайд 27Ненаправленные гипотезы
В этом случае уровень статистической значимости получается «с двумя хвостами»
распределения и называется two-tailed probability value (p value)
Слайд 29Ошибка первого рода
Ошибка, состоящая в том, что мы отклонили нуль-гипотезу, в
то время как она верна, называется
ошибкой I рода.
Вероятность такой ошибки обозначается α (или р).
ошибкой I рода.
Вероятность такой ошибки обозначается α (или р).
Слайд 30Ошибка второго рода
Ошибка, состоящая в том, что мы приняли нуль-гипотезу, в
то время как она неверна, называется ошибкой II рода.
Вероятность такой ошибки обозначается β.
Мощность критерия - это его способность не допустить ошибку II рода. Поэтому
мощность=1-β.
Мощность критерия определяется эмпирическим путем.
Вероятность такой ошибки обозначается β.
Мощность критерия - это его способность не допустить ошибку II рода. Поэтому
мощность=1-β.
Мощность критерия определяется эмпирическим путем.
Слайд 33Полезная литература:
К практическому занятию по проверке гипотез прочитать:
Сивуха С.В., Козяк А.А.
О реформе статистического вывода в психологии// Психология. Журнал высшей школы экономики. Том 6, № 4 (2009).
(есть в эл.виде в папке «Дополнительная литература»)
(есть в эл.виде в папке «Дополнительная литература»)
