- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Равенство фигур. Сравнение отрезков и углов. Биссектриса угла. (7 класс) презентация
Содержание
- 1. Равенство фигур. Сравнение отрезков и углов. Биссектриса угла. (7 класс)
- 2. Сравнение фигур с помощью наложения Ф2 Ф2
- 3. Сравнение отрезков А В С D
- 4. C A B О Решение задач. №
- 5. Середина отрезка А В
- 6. Решение задач. № 19 А В О
- 7. В М А Совместились вершины В
- 8. В М А Совместились вершины
- 9. В М А Совместились вершины
- 10. Сравнение углов А О В С
- 11. Решение задач. № 21. Дано: ОС
- 12. В М А
- 13. Решение задач. № 22. h
Слайд 1Л.С. Атанасян Геометрия 7 класс.
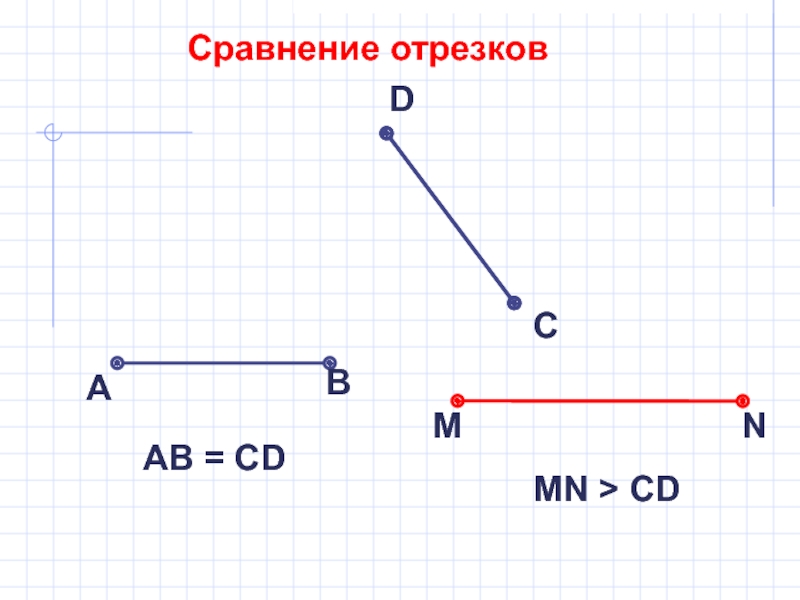
Равенство фигур. Сравнение отрезков.
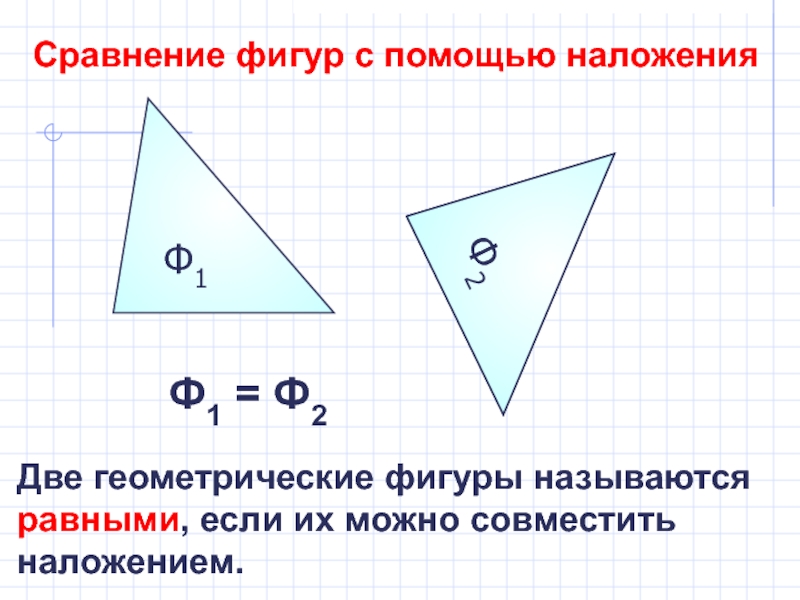
Слайд 2Сравнение фигур с помощью наложения
Ф2
Ф2
Ф1
Ф1 = Ф2
Две геометрические фигуры называются равными,
Слайд 4C
A
B
О
Решение задач. № 18
D
Дано: OD – луч,
Сравнить: ОВ и ОА;
Решение.
Т.к. точка В лежит на отрезке ОА, то отрезок ОВ является частью отрезка ОА. Значит, ОВ < OA.
Т.к. точка А лежит на отрезке ОС, то отрезок ОА является частью отрезка ОС. Значит, ОА < OС.
Т.к. точка В лежит на отрезке ОС, то отрезок ОВ является частью отрезка ОС. Значит, ОВ < OС.
Слайд 5
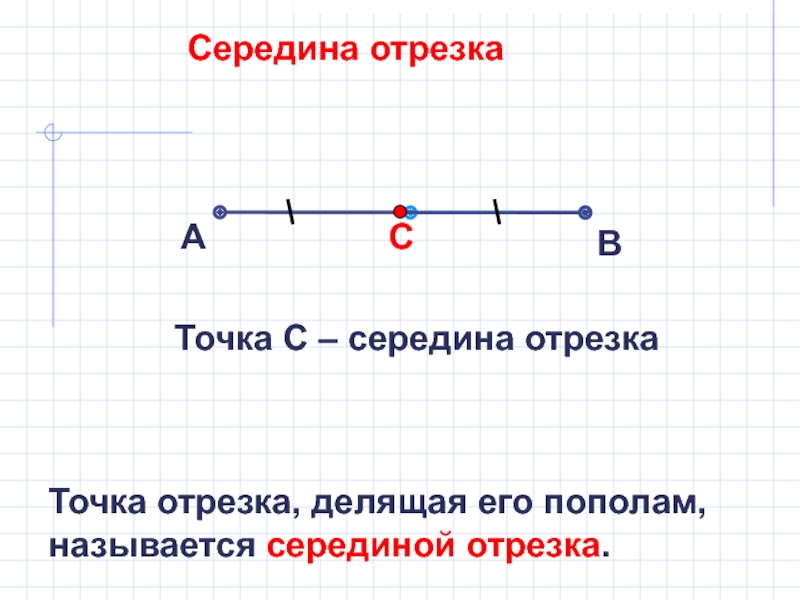
Середина отрезка
А
В
Точка С – середина отрезка
Точка отрезка, делящая его пополам,
Слайд 6Решение задач. № 19
А
В
О
Дано: АВ – отрезок,
О – середина АВ
Можно ли
а) ОА и ОВ; б) ОА и АВ.
Решение.
а) Т.к. О – середина АВ, то ОА = ОВ.
Значит, отрезки ОА и ОВ можно совместить наложением.
б) Т.к. точка О лежит на отрезке АВ, то отрезок АО является частью отрезка АВ. Значит, ОА < АВ.
Следовательно, отрезки ОА и ОВ нельзя совместить наложением.
Слайд 7
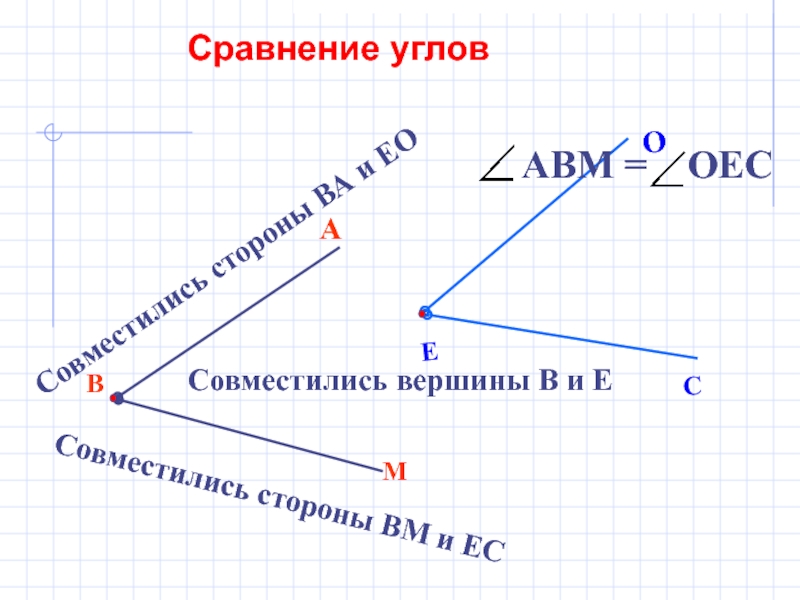
В
М
А
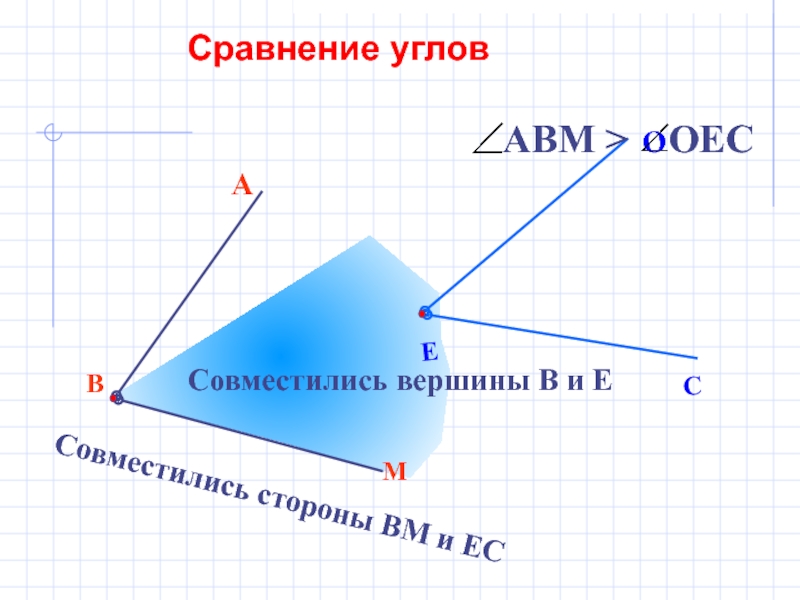
Совместились вершины В и Е
Совместились стороны ВА и ЕО
Совместились стороны ВМ
Сравнение углов
Слайд 10Сравнение углов
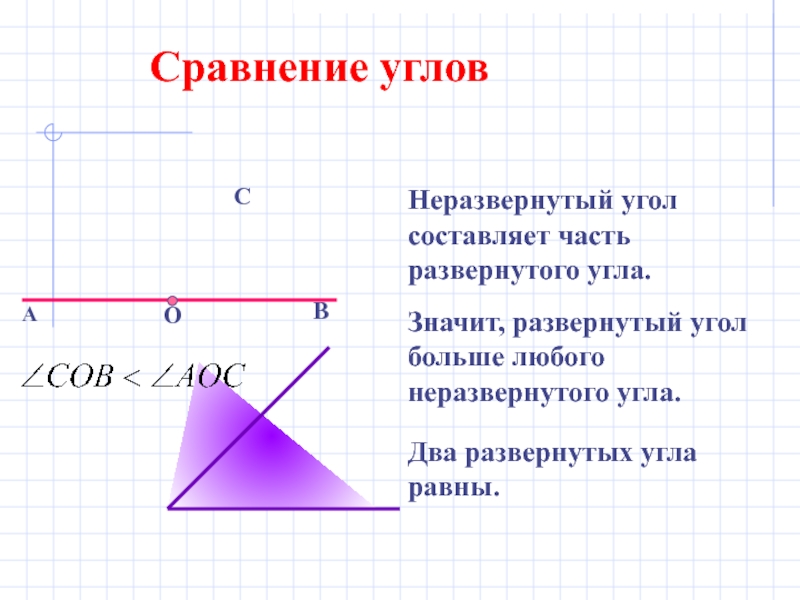
А
О
В
С
Неразвернутый угол составляет часть развернутого угла.
Значит, развернутый угол больше любого
Два развернутых угла равны.
Слайд 11Решение задач. № 21.
Дано:
ОС – луч, лежит внутри
Сравнить:
А
О
В
С
Решение.
Т.к. луч
Значит, угол АОВ больше угла АОС.
Слайд 12
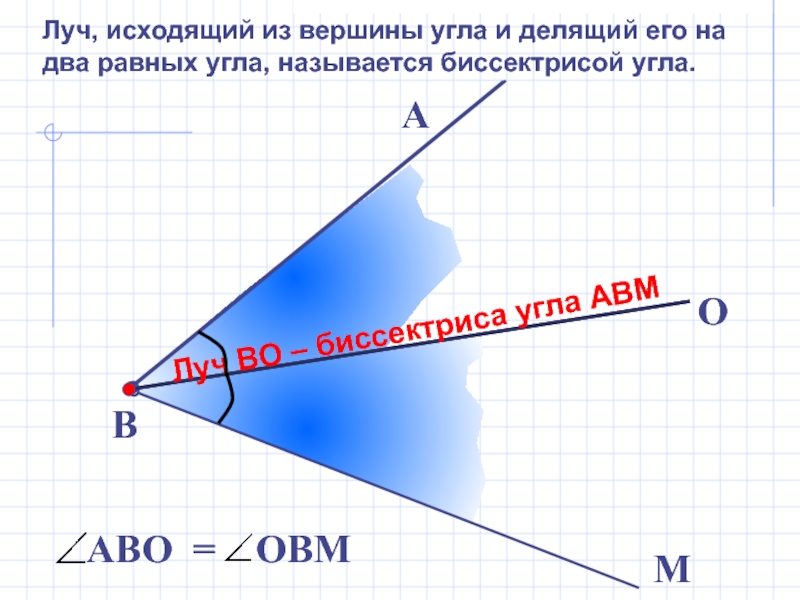
В
М
А
O
Луч ВО – биссектриса угла АВМ
Луч, исходящий из вершины угла и
Слайд 13Решение задач. № 22.
h
k
l
Дано:
Луч l - биссектриса
Можно ли совместить наложением:
Решение.
а)
Значит, эти углы hl и lk можно совместить наложением
б) Луч l проходит внутри угла hk,
значит, угол hl составляет часть угла hk,
Углы hl и hk нельзя совместить наложением