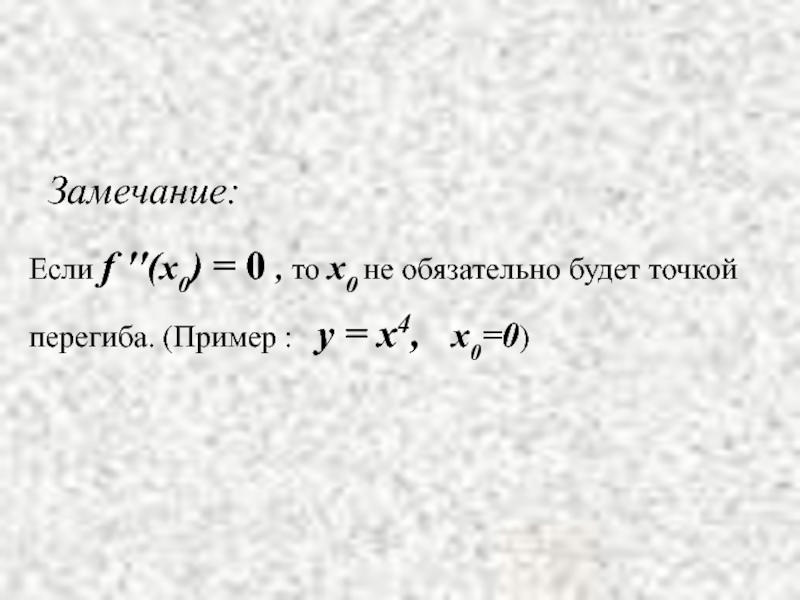- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исследование функций с помощью производной презентация
Содержание
- 1. Исследование функций с помощью производной
- 2. Лекция 1 2. Экстремум функции. Необходимое
- 3. 6. Точки перегиба. 8. Общая схема
- 4. Для того чтобы дифференцируемая на (а,в)
- 5. Локальные максимумы и минимумы функции называется её
- 7. Геометрический смысл теоремы Если в
- 8. Пример, иллюстрирующий необходимость условия: f(x)=x3;
- 9. Следствия. Если f(x) дифференцируема на (a,b), то
- 10. Точка x0 является точкой экстремума f(x), если
- 11. Пример. x y f(x)= |x|; В
- 12. Пусть f(x) непрерывна на (a,b) и
- 13. 4. По характеру смены знака f '(x)
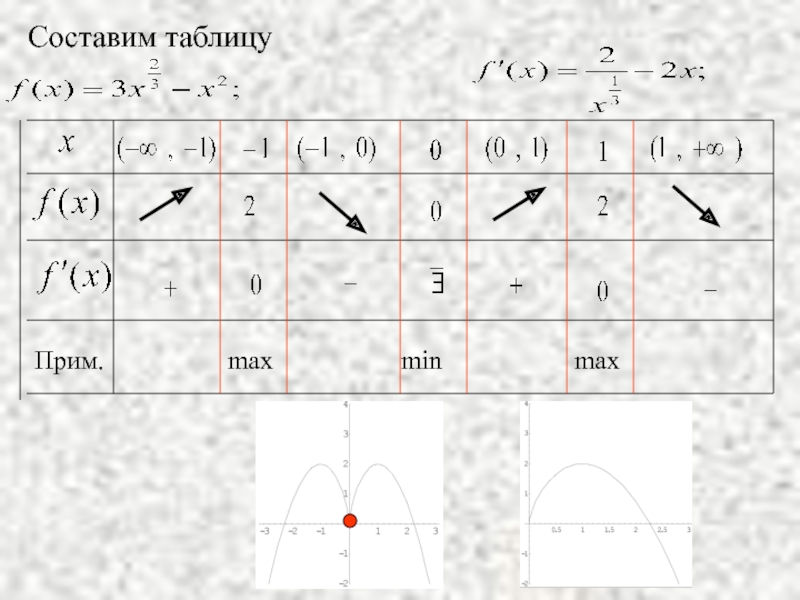
- 14. Прим. max min max Составим таблицу
- 15. Тогда: с - точка локального минимума
- 16. Доказательство:
- 17. Пусть f(x) имеет в критической точке x=c
- 18. Пример. a - точка локального минимума.
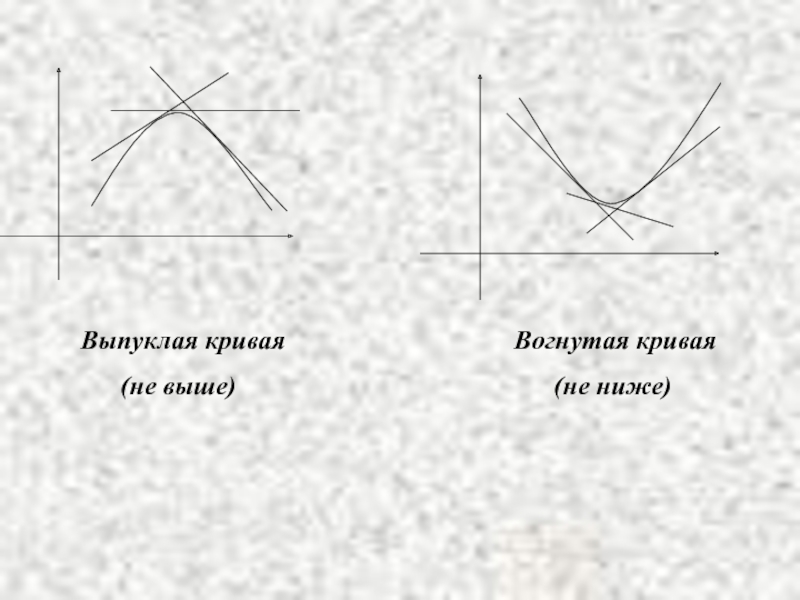
- 20. Выпуклая кривая (не выше) Вогнутая кривая (не ниже)
- 21. Если во всех точках (a,b) f
- 23. Если точка x0 является точкой
- 24. Если f ''(x0) = 0 ,
- 25. Если f ''(x) меняет знак при переходе
- 27. Замечание. Пример.
- 29. необходимо и достаточно существование пределов:
- 30. Замечание. Точно так же определяется наклонная
- 31. 2)
- 33. Исследование функции f(x) состоит из трёх этапов.
- 34. 3. Асимптоты. 4. Точки пересечения с
- 35. V. Построение Графика. Вначале проводятся асимптоты,
- 36. 2. Функция общего вида.
- 37. Прим. max перегиб
- 40. 2) В критических точках вычисляют значения функции.
Слайд 2
Лекция 1
2. Экстремум функции. Необходимое условие
существования экстремума.
3. Первый достаточный
4. Общая схема отыскания экстремума.
Условие монотонности функции.
Исследование функций с помощью производной.
Слайд 3
6. Точки перегиба.
8. Общая схема построения графика.
5. Исследование на экстремум
производных высших порядков.
9. Отыскание наибольшего и наименьшего значения функции на отрезке.
7. Асимптоты .
Слайд 4Для того чтобы дифференцируемая на (а,в)
функция f(x) не убывала (не
необходимо и достаточно, чтобы её производная
f '(x) на этом интервале была неотрицательной
(неположительной).
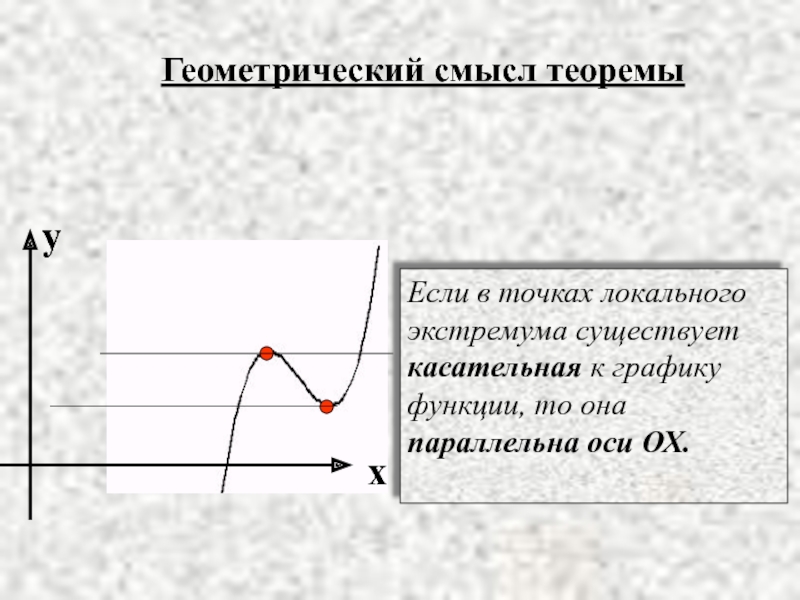
Слайд 7Геометрический смысл теоремы
Если в точках локального
экстремума существует
касательная к графику
функции,
параллельна оси ОХ.
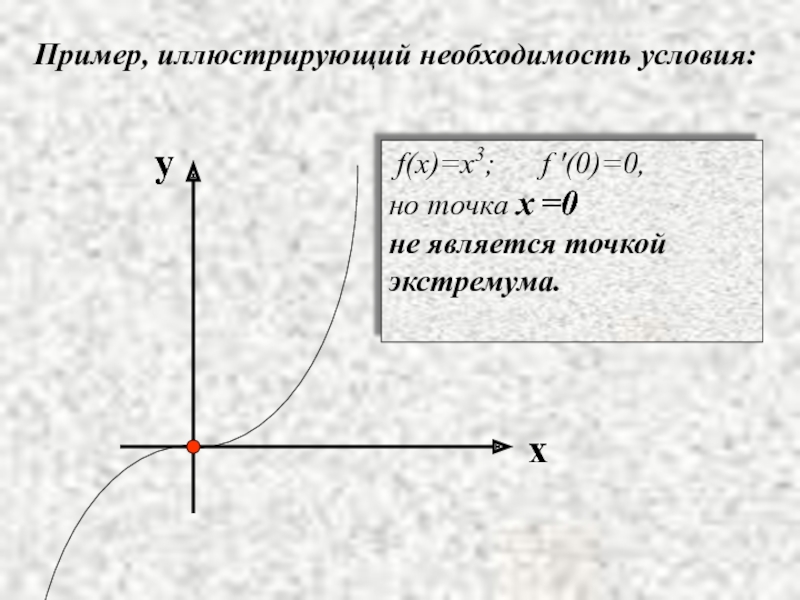
Слайд 8Пример, иллюстрирующий необходимость условия:
f(x)=x3; f '(0)=0,
но точка
не является точкой экстремума.
Слайд 9Следствия.
Если f(x) дифференцируема на (a,b), то она может
иметь
f(x) может иметь экстремумы и в точках, где
производная не существует, или равна бесконечности.
локальный минимум
локальный максимум
Точки, в которых производная равна нулю, бесконечности, или не существует называются критическими точками .
Слайд 10Точка x0 является точкой экстремума f(x), если её производная f '(x)
эту точку.
При смене знака с + на - в точке x0- максимум,
при смене знака с - на + в точке x0- минимум.
Если производная f '(x) не меняет знака при переходе через точку x0 , то экстремума в этой точке нет.
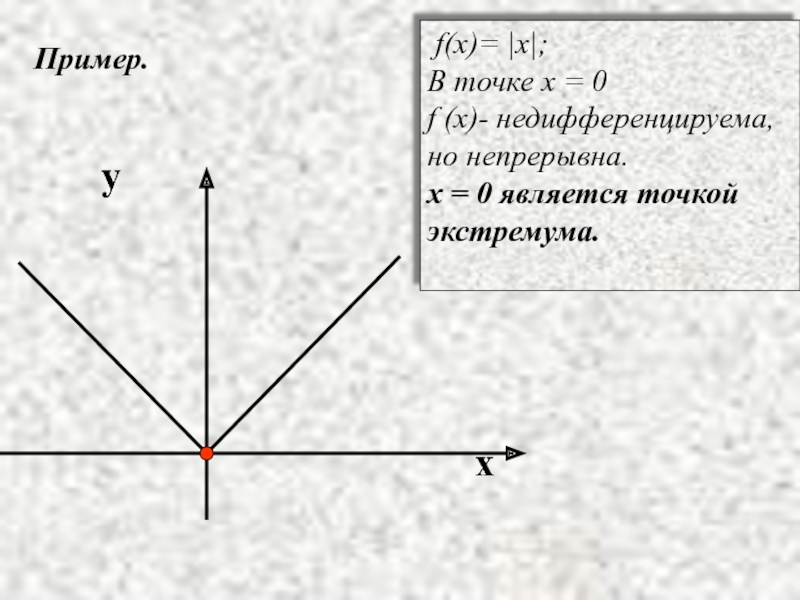
Слайд 11Пример.
x
y
f(x)= |x|;
В точке x = 0
f (x)- недифференцируема,
но непрерывна.
x
Слайд 12Пусть f(x) непрерывна на (a,b) и дифференцируема всюду за исключением
1.Находим точки x1 ,x2 , …, xn возможного экстремума (критические точки) – в них производная либо равна нулю, либо не cуществует, либо равна бесконечности.
2. Разбиваем (a,b) на интервалы монотонности
(a , x1 ) , (x1 , x2 ) , …, (xn , b),
в каждом из которых производная f '(x) сохраняет знак.
3. Определяем знак f '(x) в каждом из этих интервалов.
Слайд 134. По характеру смены знака f '(x) при переходе через
min) , либо его отсутствие.
Пример.
Слайд 15Тогда:
с - точка локального минимума
1) если f ''(c) > 0,
2) если f ''(c) < 0, то
с - точка локального максимума
Слайд 17Пусть f(x) имеет в критической точке x=c отличную от нуля
а все производные более низкого порядка при этом
равны нулю:
Тогда:
с - точка локального минимума
1) если f (2n) (c) > 0, то
с - точка локального максимума
f ' (c) = f ''(c) = … = f (2n-1) (c) = 0,
2) если f (2n) (c) < 0, то
3) если же первая отличная от нуля производная будет нечётная, то экстремума в такой критической точке нет.
Слайд 21Если во всех точках (a,b) f ''(x) < 0,то график
Пример.
График f (x) - выпуклая линия
Если во всех точках (a,b) f ''(x) > 0,то график f (x)
на (a,b) является вогнутым.
Слайд 23 Если точка x0 является точкой перегиба графика
функции y=f(x)
f ''(x0) не существует.
Слайд 24 Если f ''(x0) = 0 , то x0 не обязательно
перегиба. (Пример : y = x4, x0=0)
Замечание:
Слайд 25Если f ''(x) меняет знак при переходе через точку x0,
то эта
если f ''(x) не меняет знак при переходе через точку x0,
то в этой точке перегиба нет.
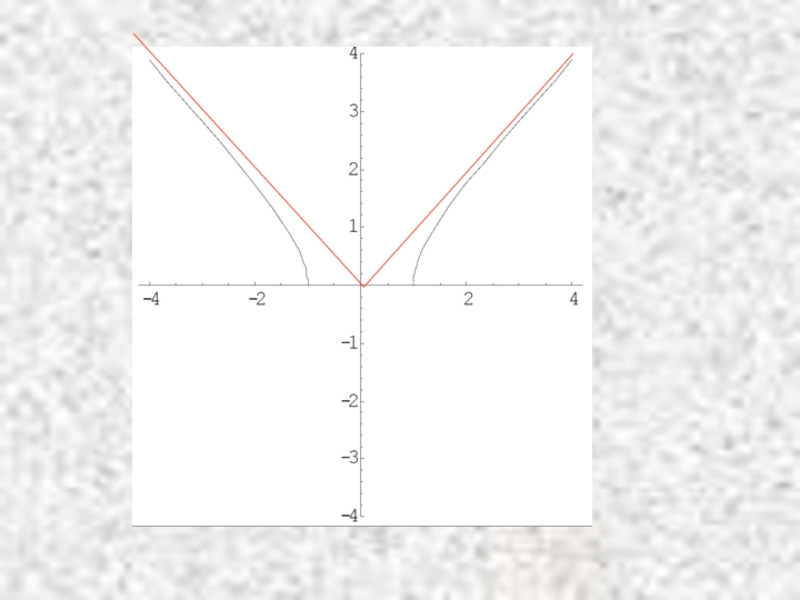
Слайд 30Замечание.
Точно так же определяется наклонная асимптота и
формулируется критерий
Пример.
Найти асимптоты функции
Решение.
Функция непрерывна в любой точке области определения ⇒
Вертикальных асимптот нет!
Слайд 33Исследование функции f(x) состоит из трёх этапов.
1. Область определения.
I. Информация
2. Чётность
или
периодичность
сужение области изменения x для дальнейшего исследования.
Слайд 343. Асимптоты.
4. Точки пересечения с осями координат.
II. Информация из
( Исследование на экстремум)
III. Информация из вида f ''(x).
(Нахождение точек перегиба)
IV. Таблица.
Слайд 35V. Построение Графика.
Вначале проводятся асимптоты, ставятся опорные точки, найденные на
Пример.
Слайд 402) В критических точках вычисляют значения функции.
3) Вычисляют значения функции на
4) Из всех вычисленных значений функции выбирают наибольшее и наименьшее.