- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исследование функций методами дифференциального исчисления. Условие постоянства функции презентация
Содержание
- 1. Исследование функций методами дифференциального исчисления. Условие постоянства функции
- 2. Теорема 1. Для того, чтобы функция Теорема
- 3. Доказательство. Необходимость. Достаточность. Теорема Лагранжа (§9)
- 4. п.2. Монотонность функции. Теорема 2. (Достаточное условие
- 5. Доказательство. Теорема Лагранжа §9 функция
- 6. Самостоятельно: доказать теорему в случае убывания функции.
- 7. п.3. Локальный экстремум. Точка называется
- 8. Точки локального максимума и локального минимума называются
- 9. Доказательство. ─ точка локального максимума
- 10. Самостоятельно: доказать теорему в случае точки локального минимума.
- 11. Замечание 1. Необходимое условие не является достаточным.
- 12. Замечание 1. Функция может иметь экстремум в
- 13. Пример. x O y ─ точка локального минимума
- 14. Теорема 4. (Первое достаточное условие локального экстремума)
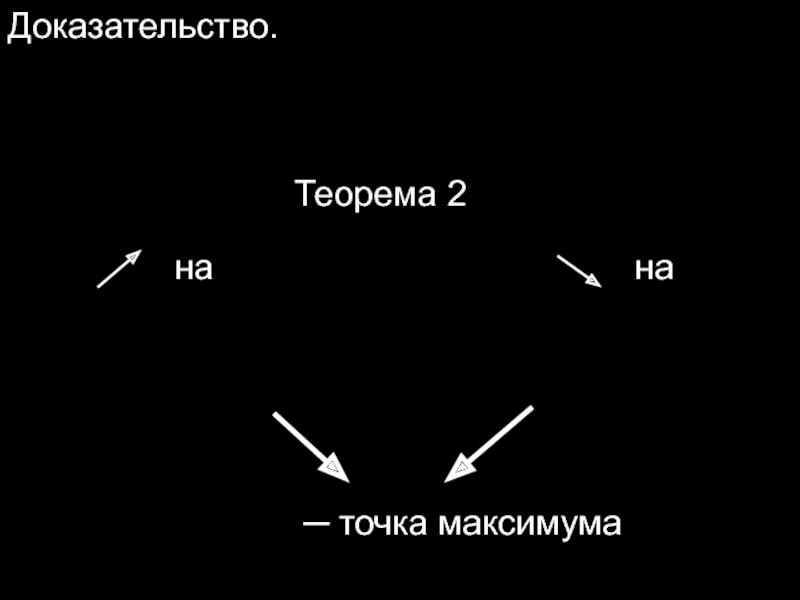
- 15. Доказательство. Теорема 2 на на ─ точка максимума
- 16. x O y
- 17. Самостоятельно: доказать теорему в случае точки минимума.
- 18. Теорема 5. (Второе достаточное условие локального экстремума)
- 19. Доказательство. Теорема 4 ─ точка минимума
- 20. Самостоятельно: доказать теорему в случае точки максимума.
- 21. п.4. Наибольшее и наименьшее значение функции на
- 22. Алгоритм поиска наибольшего и наименьшего значения функции
- 23. п.5. Выпуклость (вогнутость) графика функции. Пусть Тогда
- 24. Функция
- 25. Функция
- 26. Теорема 6. (Достаточное условие выпуклости) Пусть Тогда
- 27. Доказательство. §10 п.2
- 28. Самостоятельно: доказать теорему в случае выпуклой функции.
- 29. п.6. Точки перегиба. Точкой перегиба графика непрерывной
- 30. Теорема 7. (Необходимое условие точки перегиба) Пусть
- 31. Замечание 3. Необходимое условие не является достаточным. Пример. x O y не является точкой перегиба.
- 32. Замечание 4. Точки перегиба ─ это точки экстремума первой производной функции.
- 33. Теорема 8. (Достаточное условие точки перегиба) Если
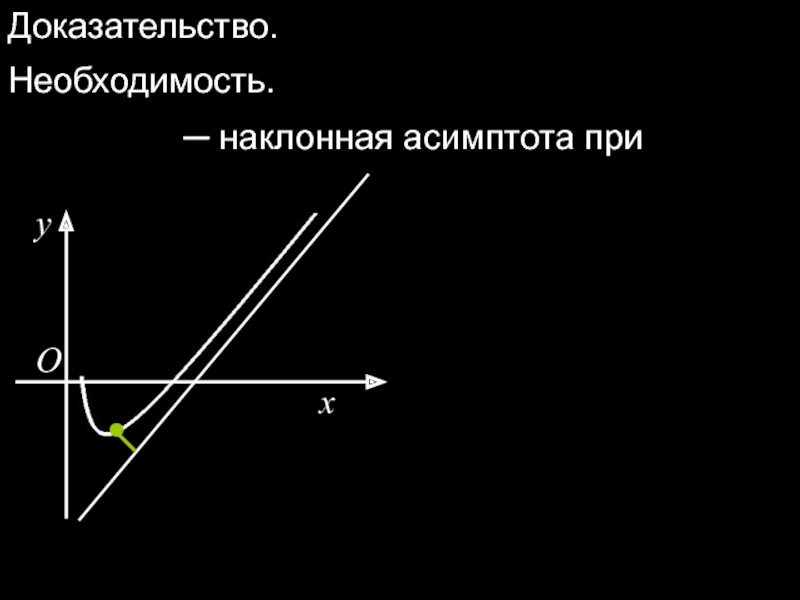
- 34. п.7. Асимптоты. Асимптотой кривой называется прямая,
- 35. Прямая является
- 36. Прямая является
- 37. Уравнение наклонной асимптоты: Теорема 9. Для того,
- 38. Доказательство. Необходимость. ─ наклонная асимптота при x O y
- 39. Теорема 2 §6 ─ БМФ при
- 40. Достаточность. Теорема 2 §6 ─ БМФ при ─ наклонная асимптота
Слайд 1§19. Исследование функций методами дифференциального исчисления
п.1. Условие постоянства функции.
Слайд 2Теорема 1. Для того, чтобы функция
Теорема 1. Для того, чтобы функция
Теорема 1. Для того, чтобы функция дифференцируемая на X, была постоянной на X, необходимо и достаточно, чтобы
Слайд 4п.2. Монотонность функции.
Теорема 2. (Достаточное условие монотонности)
Пусть
Тогда
функция
функция возрастает (убывает) на интервале
Слайд 7п.3. Локальный экстремум.
Точка называется точкой локального максимума функции
Точка называется точкой локального максимума функции , если существует некоторая окрестность точки
Точка называется точкой локального максимума функции , если существует некоторая окрестность точки такая, что для всех из этой окрестности выполняется неравенство
Самостоятельно: определить точку локального минимума.
Слайд 8Точки локального максимума и локального минимума называются точками локального экстремума.
Теорема 3.
Пусть
Тогда
функция дифференцируема,
─ точка локального экстремума.
Слайд 11Замечание 1. Необходимое условие не является достаточным.
Пример.
x
O
y
не является точкой локального экстремума
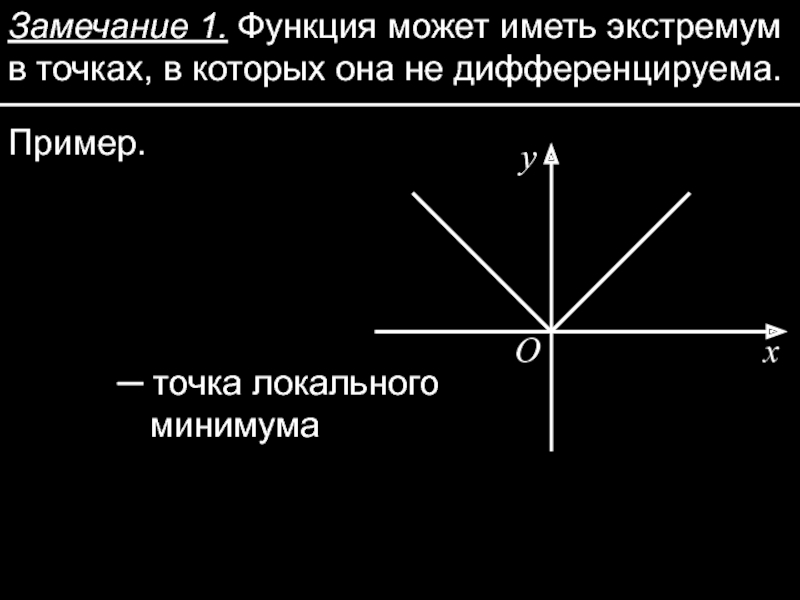
Слайд 12Замечание 1. Функция может иметь экстремум в точках, в которых она
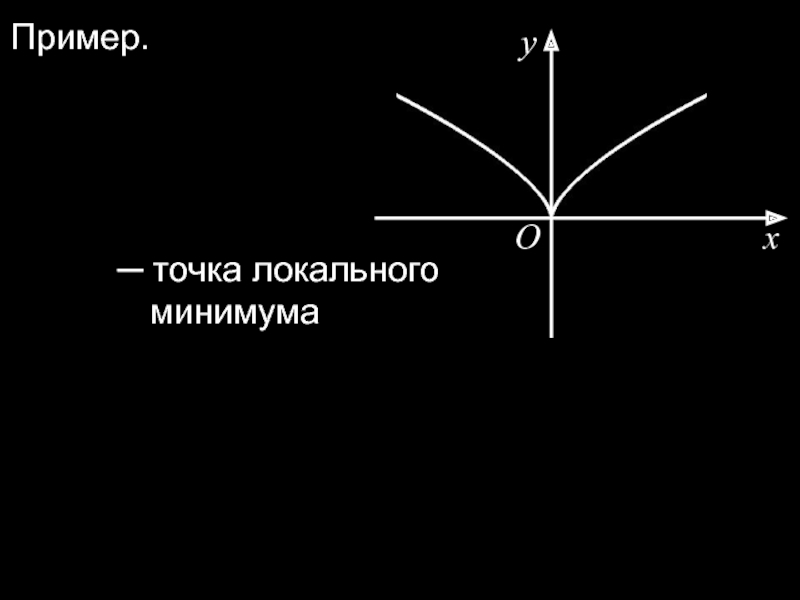
Пример.
x
O
y
─ точка локального минимума
Слайд 14Теорема 4. (Первое достаточное условие локального экстремума)
Если при переходе через точку
Если при переходе через точку производная дифференцируемой функции меняет знак с плюса на минус, то ─ точка максимума,
Если при переходе через точку производная дифференцируемой функции меняет знак с плюса на минус, то ─ точка максимума, а если с минуса на плюс, то ─ точка минимума.
Слайд 18Теорема 5. (Второе достаточное условие локального экстремума)
Пусть
Тогда,
если
если , то ─ точка минимума.
Слайд 21п.4. Наибольшее и наименьшее значение функции на отрезке.
Пусть функция
По теореме Вейерштрасса она достигает на этом отрезке своего наибольшего и наименьшего значения.
Эти значения функция может принимать либо во внутренней точке отрезка, либо на его границе.
Слайд 22Алгоритм поиска наибольшего и наименьшего значения функции
1. Найти критические точки (точки,
2. Вычислить значения функции в найденных критических точках и на концах отрезка.
3. Среди вычисленных значений выбрать наибольшее и наименьшее.
Слайд 23п.5. Выпуклость (вогнутость) графика функции.
Пусть
Тогда
функция
в каждой точке ее графика существует касательная.
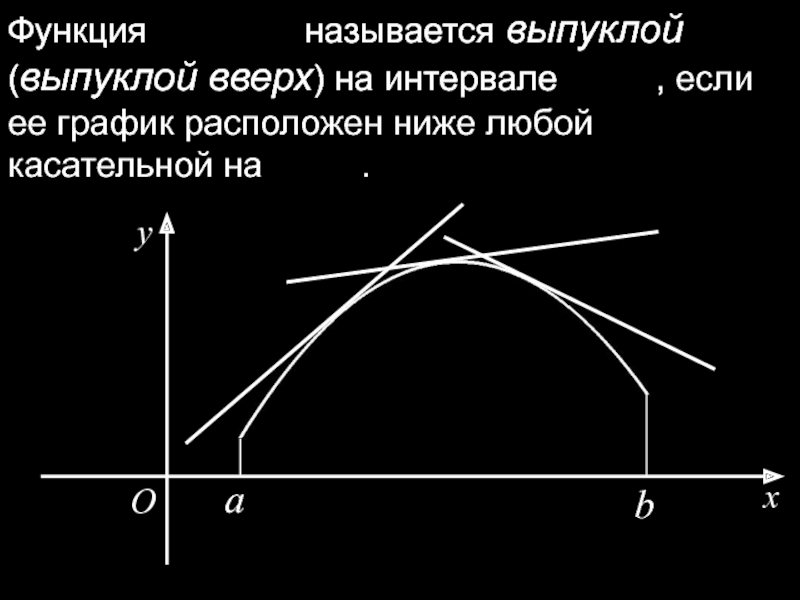
Слайд 24Функция называется выпуклой (выпуклой
Функция называется выпуклой (выпуклой вверх) на интервале , если ее график расположен ниже любой касательной на .
x
O
y
a
b
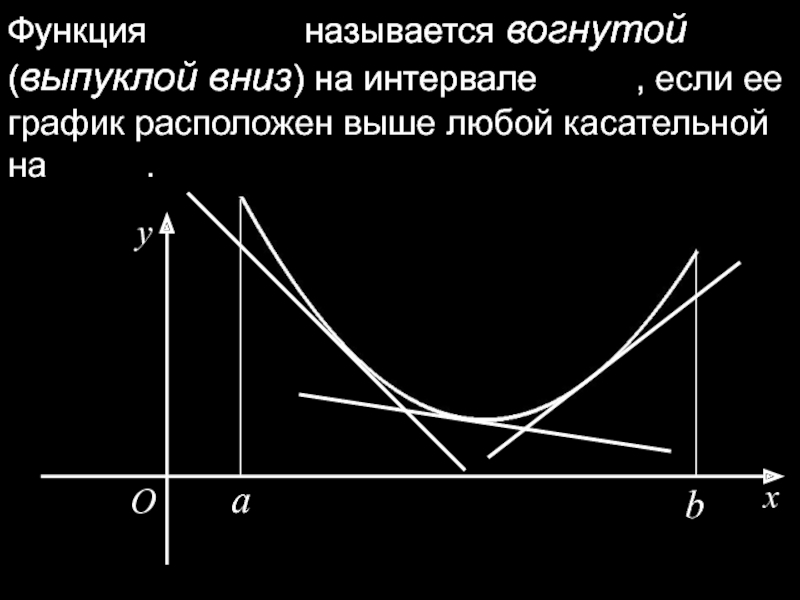
Слайд 25Функция называется вогнутой (выпуклой
Функция называется вогнутой (выпуклой вниз) на интервале , если ее график расположен выше любой касательной на .
x
O
y
a
b
Слайд 26Теорема 6. (Достаточное условие выпуклости)
Пусть
Тогда
функция
функция выпукла (вогнута) на интервале
Слайд 29п.6. Точки перегиба.
Точкой перегиба графика непрерывной функции называется точка,
Точкой перегиба
Слайд 30Теорема 7. (Необходимое условие точки перегиба)
Пусть
Тогда
функция
─ точка перегиба.
Слайд 31Замечание 3. Необходимое условие не является достаточным.
Пример.
x
O
y
не является точкой перегиба.
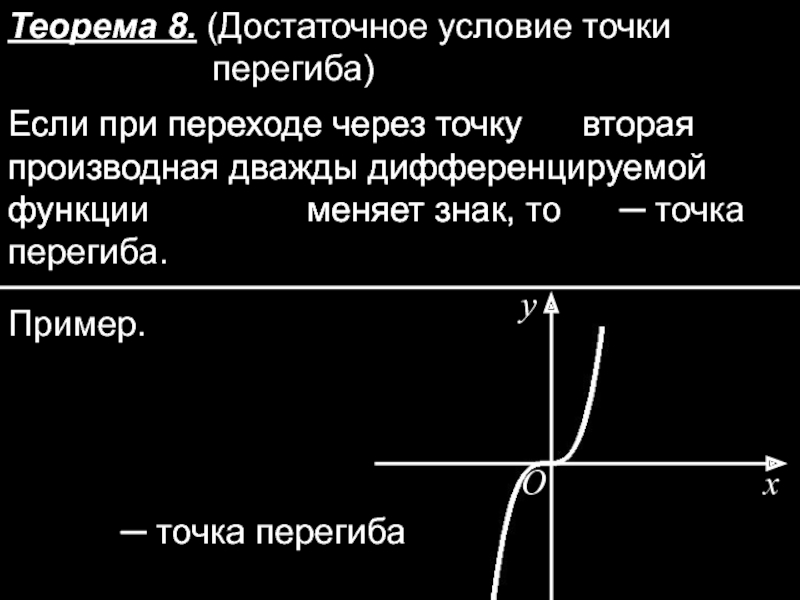
Слайд 33Теорема 8. (Достаточное условие точки перегиба)
Если при переходе через точку
Если при переходе через точку вторая производная дважды дифференцируемой функции меняет знак, то ─ точка перегиба.
Пример.
x
O
y
─ точка перегиба
Слайд 34п.7. Асимптоты.
Асимптотой кривой называется прямая,
Асимптотой кривой называется прямая, расстояние до
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.
Слайд 35Прямая является вертикальной асимптотой графика функции
Прямая является вертикальной асимптотой графика функции , если хотя бы один из односторонних пределов функции в этой точке равен .
Пример.
─ вертикальная асимптота
x
O
y
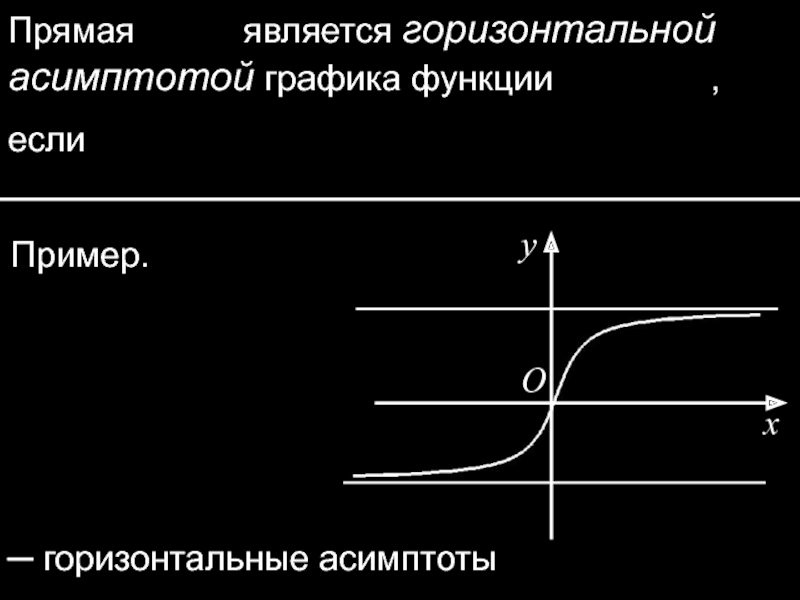
Слайд 36Прямая является горизонтальной асимптотой графика функции
Пример.
─ горизонтальные асимптоты
x
O
y
если
Слайд 37Уравнение наклонной асимптоты:
Теорема 9. Для того, чтобы график функции
необходимо и достаточно, чтобы существовали конечные пределы