Элементы аналитической геометрии презентация

Содержание

1. Элементы аналитической геометрии
2. Линии на плоскости
3. Линии на плоскости
4. Линии на плоскости
5. Линии на плоскости
6. Линии на плоскости
7. Линии на плоскости
8. Линии на плоскости
9. Линии на плоскости
10. Линии на плоскости
11. Линии на плоскости
12. Линии и поверхности в пространстве
13. Линии и поверхности в пространстве
14. Линии и поверхности в пространстве
15. Линии и поверхности в пространстве
16. Линии и поверхности в пространстве
17. Линии и поверхности в пространстве
18. Линии и поверхности в пространстве
19. Линии и поверхности в пространстве
20. Линии и поверхности в пространстве
21. Линии и поверхности в пространстве
22. Линии и поверхности в пространстве
23. Линии и поверхности в пространстве

Линии на плоскости Уравнением линии на плоскости ОХУ называется такое уравнение F(x,y)=0, которому удовлетворяют координаты х и у в каждой точке линии и не удовлетворяют координаты

Главная
Математика
Элементы аналитической геометрии

Слайд 1

Элементы аналитической геометрии

Линии на плоскости
Окружность. Эллипс. Гипербола. Парабола
Линии

и поверхности в пространстве
Цилиндрические поверхности. Поверхности вращения.

Слайд 2
Линии на плоскости

Уравнением линии на плоскости ОХУ называется
такое уравнение F(x,y)=0, которому

удовлетворяют
координаты х и у в каждой точке линии и не
удовлетворяют координаты любой точки, не
лежащей на этой линии

Определение

Всякое уравнение первой степени относительно х
и у вида Ax+By+C=0, где A, B, C – постоянные
коэффициенты, причем определяет на
плоскости некоторую прямую

Слайд 3

Линии на плоскости

Рассмотрим произвольную точку M(x, y).
Точка

тогда и только тогда, когда

общее уравнение прямой на
плоскости

Рассмотрим прямую и точку .

Слайд 4

Линии на плоскости

Кривой второго порядка называется линия,
определяемая уравнением второй степени

относительно текущих координат

Определение

Все коэффициенты действительные числа,
причем хотя бы одно из чисел A,B,C отлично от
нуля

Слайд 5
Линии на плоскости

Окружностью называется множество точек
плоскости, находящихся на одинаковом
расстоянии,

называемом радиусом, от
фиксированной точки, называемой центром
окружности

Определение

УРАВНЕНИЕ ОКРУЖНОСТИ

- центр окружности

- радиус окружности

Слайд 6
Линии на плоскости

Эллипсом называется множество точек плоскости,
сумма расстояний от которых до

двух данных
точек и , называемых фокусами, есть
величина постоянная, причем эта постоянная
больше расстояния между фокусами

Определение

Слайд 7
Линии на плоскости

УРАВНЕНИЕ ЭЛЛИПСА
Если фокусы эллипса располагаются в точках

, то каноническое уравнение эллипса имеет вид

Числа a>0, b >0 называются большой и малой полуосями эллипса, причем .

Слайд 8
Линии на плоскости

Гиперболой называется множество точек
плоскости, абсолютная величина разности
расстояний

от которых до двух данных точек
и , называемых фокусами, есть величина
постоянная, причем эта постоянная меньше
расстояния между фокусами

Определение

Слайд 9
Линии на плоскости

УРАВНЕНИЕ ГИПЕРБОЛЫ
Если фокусы гиперболы располагаются в точках

, то каноническое уравнение гиперболы имеет вид

, где

Слайд 10
Линии на плоскости

Параболой называется множество точек
плоскости, равноудаленных от данной точки

F,
называемой фокусом, и данной прямой m,
называемой директрисой

Определение

Слайд 11
Линии на плоскости

УРАВНЕНИЕ ПАРАБОЛЫ
Если прямая m:

, а ,

то каноническое уравнение параболы имеет вид

, где

Слайд 12
Линии и поверхности в пространстве

Уравнением поверхности в прямоугольной системе
координат OXYZ называется

такое уравнение
F(x,y,z)=0, которому удовлетворяют координаты
любой точки, принадлежащей поверхности, и не
удовлетворяют координаты любой точки, не
принадлежащей поверхности

Определение

Всякое линейное уравнение с тремя переменными
вида Ax+By+Cz+D=0, где A, B, C, D – постоянные
коэффициенты, причем определяет
в пространстве некоторую плоскость

Слайд 13
Линии и поверхности в пространстве

Рассмотрим плоскость .
общее уравнение

плоскости
в пространстве

Слайд 14
Линии и поверхности в пространстве

Общее уравнение прямой в пространстве
Прямая в пространстве

может быть задана
уравнениями двух плоскостей, пересекающихся по этой прямой, то есть в виде системы

Слайд 15
Линии и поверхности в пространстве

каноническое уравнение
прямой в пространстве
Каноническое уравнение прямой

в пространстве

Слайд 16

Линии и поверхности в пространстве

Поверхность, образованная движением прямой L,
которая перемещается в

пространстве, сохраняя
постоянное направление и пересекая каждый раз
некоторую кривую К, называется цилиндрической
поверхностью или цилиндром.

Цилиндрические поверхности

Определение

кривая К – направляющая цилиндра
прямая L – образующая цилиндра

Слайд 17
Линии и поверхности в пространстве

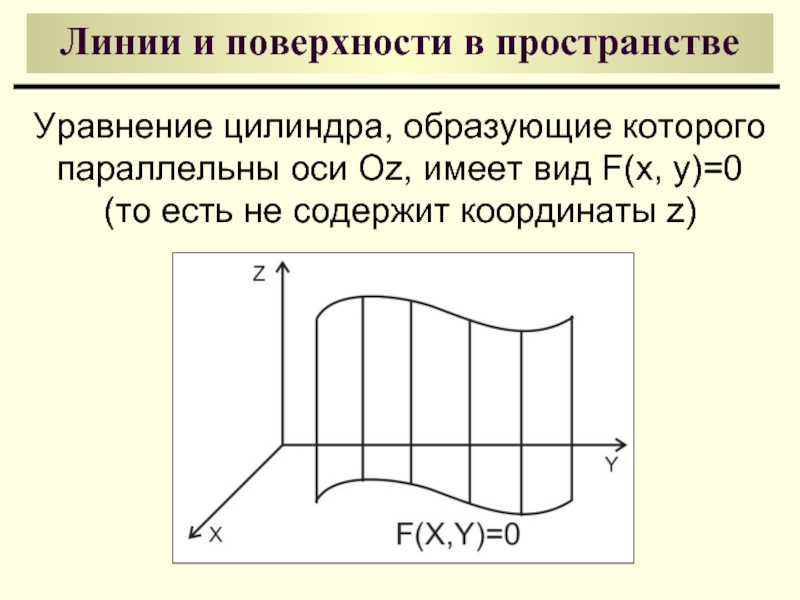
Уравнение цилиндра, образующие которого
параллельны оси Оz, имеет

вид F(x, y)=0
(то есть не содержит координаты z)

Слайд 18
Линии и поверхности в пространстве

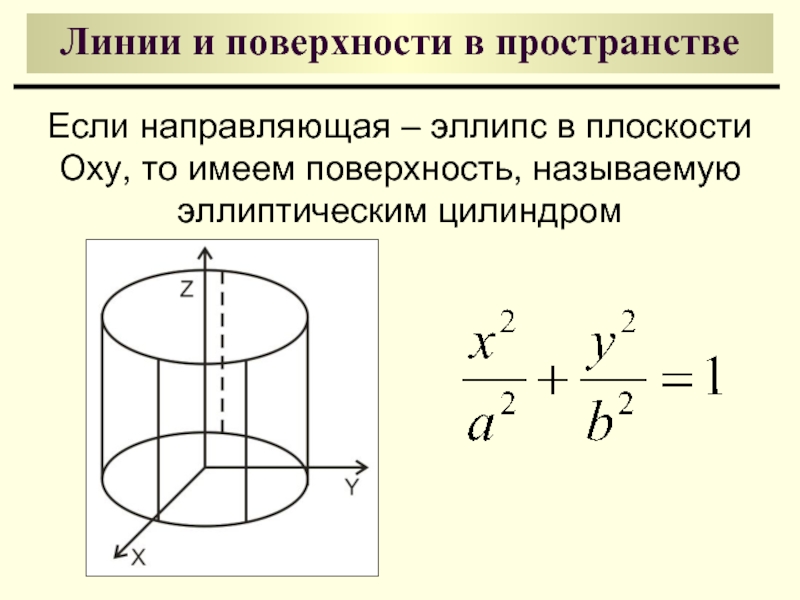
Если направляющая – эллипс в плоскости Oxy,

то имеем поверхность, называемую эллиптическим цилиндром

Слайд 19
Линии и поверхности в пространстве

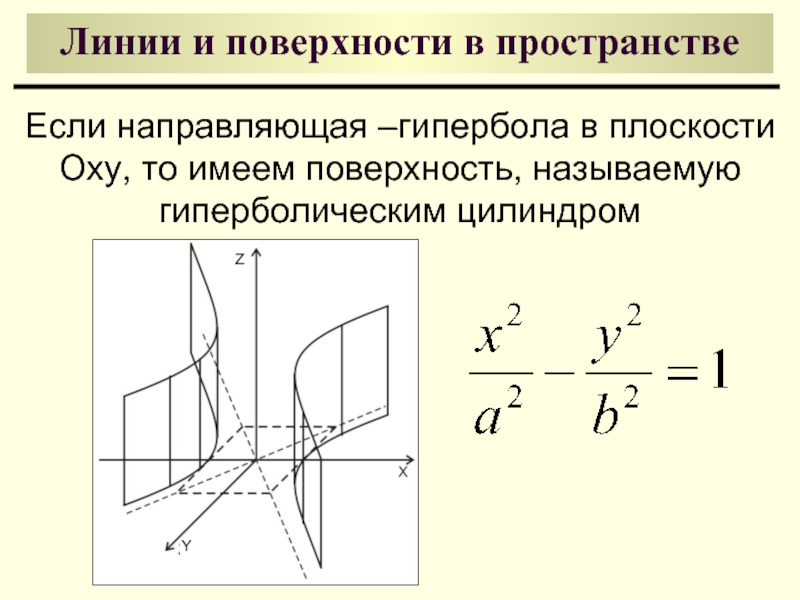
Если направляющая –гипербола в плоскости Oxy, то

имеем поверхность, называемую гиперболическим цилиндром

Слайд 20
Линии и поверхности в пространстве

Поверхность, образованная вращением некоторой
плоской кривой вокруг оси,

лежащей в ее
плоскости называется поверхностью вращения

Поверхности вращения

Определение

Слайд 21
Линии и поверхности в пространстве

Пусть некоторая кривая L лежит в плоскости

Oyz. Уравнение этой кривой имеет вид:

Поверхность, образованная вращением кривой L вокруг оси Oz, имеет вид:

Слайд 22
Линии и поверхности в пространстве

Если вращать кривую, заданную уравнением
- вокруг

оси Ox, то поверхность задается уравнением

- вокруг оси Oy, то поверхность задается уравнением

Слайд 23
Линии и поверхности в пространстве

- эллипсоид вращения
- параболоид вращения
Примеры:
Oz - ось

вращения

Скачать презентацию

Элементы аналитической геометрии презентация

Содержание

Слайд 1

Элементы аналитической геометрии

Линии на плоскости
Окружность. Эллипс. Гипербола. Парабола
Линии

Слайд 2
Линии на плоскости

Уравнением линии на плоскости ОХУ называется
такое уравнение F(x,y)=0, которому

Слайд 3

Линии на плоскости

Рассмотрим произвольную точку M(x, y).
Точка

Слайд 4

Линии на плоскости

Кривой второго порядка называется линия,
определяемая уравнением второй степени

Слайд 5
Линии на плоскости

Окружностью называется множество точек
плоскости, находящихся на одинаковом
расстоянии,

Слайд 6
Линии на плоскости

Эллипсом называется множество точек плоскости,
сумма расстояний от которых до

Слайд 7
Линии на плоскости

УРАВНЕНИЕ ЭЛЛИПСА
Если фокусы эллипса располагаются в точках

Слайд 8
Линии на плоскости

Гиперболой называется множество точек
плоскости, абсолютная величина разности
расстояний

Слайд 9
Линии на плоскости

УРАВНЕНИЕ ГИПЕРБОЛЫ
Если фокусы гиперболы располагаются в точках

Слайд 10
Линии на плоскости

Параболой называется множество точек
плоскости, равноудаленных от данной точки

Слайд 11
Линии на плоскости

УРАВНЕНИЕ ПАРАБОЛЫ
Если прямая m:

Слайд 12
Линии и поверхности в пространстве

Уравнением поверхности в прямоугольной системе
координат OXYZ называется

Слайд 13
Линии и поверхности в пространстве

Рассмотрим плоскость .
общее уравнение

Слайд 14
Линии и поверхности в пространстве

Общее уравнение прямой в пространстве
Прямая в пространстве

Слайд 15
Линии и поверхности в пространстве

каноническое уравнение
прямой в пространстве
Каноническое уравнение прямой

Слайд 16

Линии и поверхности в пространстве

Поверхность, образованная движением прямой L,
которая перемещается в

Слайд 17
Линии и поверхности в пространстве

Уравнение цилиндра, образующие которого
параллельны оси Оz, имеет

Слайд 18
Линии и поверхности в пространстве

Если направляющая – эллипс в плоскости Oxy,

Слайд 19
Линии и поверхности в пространстве

Если направляющая –гипербола в плоскости Oxy, то

Слайд 20
Линии и поверхности в пространстве

Поверхность, образованная вращением некоторой
плоской кривой вокруг оси,

Слайд 21
Линии и поверхности в пространстве

Пусть некоторая кривая L лежит в плоскости

Слайд 22
Линии и поверхности в пространстве

Если вращать кривую, заданную уравнением
- вокруг

Слайд 23
Линии и поверхности в пространстве

- эллипсоид вращения
- параболоид вращения
Примеры:
Oz - ось

Обратная связь

Что такое ThePresentation.ru?

Элементы аналитической геометрии презентация

Содержание

Слайд 1Элементы аналитической геометрии Линии на плоскости Окружность. Эллипс. Гипербола. Парабола Линии

Слайд 2Линии на плоскостиУравнением линии на плоскости ОХУ называетсятакое уравнение F(x,y)=0, которому

Слайд 3Линии на плоскостиРассмотрим произвольную точку M(x, y). Точка

Слайд 4Линии на плоскостиКривой второго порядка называется линия, определяемая уравнением второй степени

Слайд 5Линии на плоскостиОкружностью называется множество точек плоскости, находящихся на одинаковом расстоянии,

Слайд 6Линии на плоскостиЭллипсом называется множество точек плоскости,сумма расстояний от которых до

Слайд 7Линии на плоскостиУРАВНЕНИЕ ЭЛЛИПСАЕсли фокусы эллипса располагаются в точках

Слайд 8Линии на плоскостиГиперболой называется множество точек плоскости, абсолютная величина разности расстояний

Слайд 9Линии на плоскостиУРАВНЕНИЕ ГИПЕРБОЛЫЕсли фокусы гиперболы располагаются в точках

Слайд 10Линии на плоскостиПараболой называется множество точек плоскости, равноудаленных от данной точки

Слайд 11Линии на плоскостиУРАВНЕНИЕ ПАРАБОЛЫЕсли прямая m:

Слайд 12Линии и поверхности в пространствеУравнением поверхности в прямоугольной системекоординат OXYZ называется

Слайд 13Линии и поверхности в пространствеРассмотрим плоскость .общее уравнение

Слайд 14Линии и поверхности в пространствеОбщее уравнение прямой в пространствеПрямая в пространстве

Слайд 15Линии и поверхности в пространстве каноническое уравнениепрямой в пространствеКаноническое уравнение прямой

Слайд 16Линии и поверхности в пространствеПоверхность, образованная движением прямой L,которая перемещается в

Слайд 17Линии и поверхности в пространствеУравнение цилиндра, образующие которогопараллельны оси Оz, имеет

Слайд 18Линии и поверхности в пространствеЕсли направляющая – эллипс в плоскости Oxy,

Слайд 19Линии и поверхности в пространствеЕсли направляющая –гипербола в плоскости Oxy, то

Слайд 20Линии и поверхности в пространствеПоверхность, образованная вращением некоторойплоской кривой вокруг оси,

Слайд 21Линии и поверхности в пространствеПусть некоторая кривая L лежит в плоскости

Слайд 22Линии и поверхности в пространствеЕсли вращать кривую, заданную уравнением - вокруг

Слайд 23Линии и поверхности в пространстве- эллипсоид вращения- параболоид вращенияПримеры:Oz - ось

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1

Элементы аналитической геометрии

Линии на плоскости
Окружность. Эллипс. Гипербола. Парабола
Линии

Слайд 2
Линии на плоскости

Уравнением линии на плоскости ОХУ называется
такое уравнение F(x,y)=0, которому

Слайд 3

Линии на плоскости

Рассмотрим произвольную точку M(x, y).
Точка

Слайд 4

Линии на плоскости

Кривой второго порядка называется линия,
определяемая уравнением второй степени

Слайд 5
Линии на плоскости

Окружностью называется множество точек
плоскости, находящихся на одинаковом
расстоянии,

Слайд 6
Линии на плоскости

Эллипсом называется множество точек плоскости,
сумма расстояний от которых до

Слайд 7
Линии на плоскости

УРАВНЕНИЕ ЭЛЛИПСА
Если фокусы эллипса располагаются в точках

Слайд 8
Линии на плоскости

Гиперболой называется множество точек
плоскости, абсолютная величина разности
расстояний

Слайд 9
Линии на плоскости

УРАВНЕНИЕ ГИПЕРБОЛЫ
Если фокусы гиперболы располагаются в точках

Слайд 10
Линии на плоскости

Параболой называется множество точек
плоскости, равноудаленных от данной точки

Слайд 11
Линии на плоскости

УРАВНЕНИЕ ПАРАБОЛЫ
Если прямая m:

Слайд 12
Линии и поверхности в пространстве

Уравнением поверхности в прямоугольной системе
координат OXYZ называется

Слайд 13
Линии и поверхности в пространстве

Рассмотрим плоскость .
общее уравнение

Слайд 14
Линии и поверхности в пространстве

Общее уравнение прямой в пространстве
Прямая в пространстве

Слайд 15
Линии и поверхности в пространстве

каноническое уравнение
прямой в пространстве
Каноническое уравнение прямой

Слайд 16

Линии и поверхности в пространстве

Поверхность, образованная движением прямой L,
которая перемещается в

Слайд 17
Линии и поверхности в пространстве

Уравнение цилиндра, образующие которого
параллельны оси Оz, имеет

Слайд 18
Линии и поверхности в пространстве

Если направляющая – эллипс в плоскости Oxy,

Слайд 19
Линии и поверхности в пространстве

Если направляющая –гипербола в плоскости Oxy, то

Слайд 20
Линии и поверхности в пространстве

Поверхность, образованная вращением некоторой
плоской кривой вокруг оси,

Слайд 21
Линии и поверхности в пространстве

Пусть некоторая кривая L лежит в плоскости

Слайд 22
Линии и поверхности в пространстве

Если вращать кривую, заданную уравнением
- вокруг

Слайд 23
Линии и поверхности в пространстве

- эллипсоид вращения
- параболоид вращения
Примеры:
Oz - ось