- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
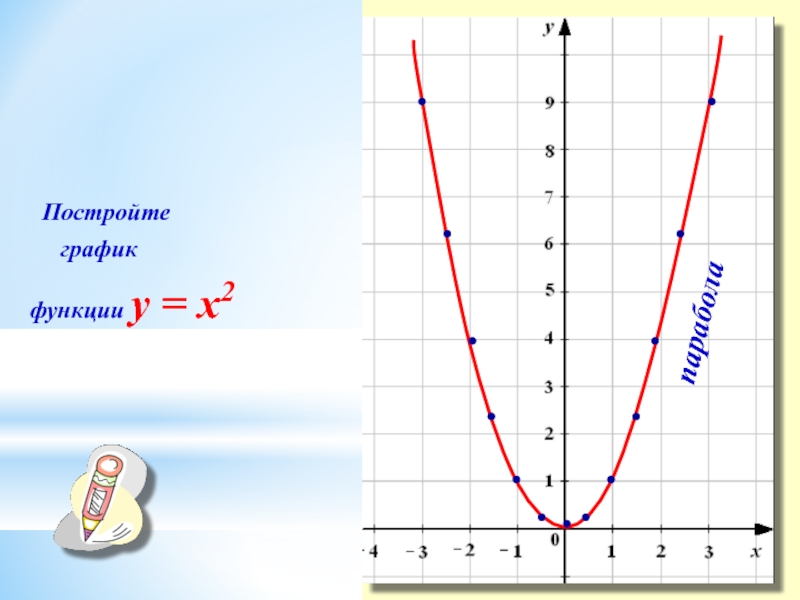
Функция y = x2 и её график презентация
Содержание
- 1. Функция y = x2 и её график
- 2. Назовите координаты точек, симметричных данным точкам
- 3.
- 4. На графике видно, что ось OY делит
- 5.
- 6. График функции y = x 2 + 3 —
- 7. Найдите значение функции
- 9. Постройте графики функций: 1).У=2Х+3 2).У=-2Х-1; 3).
- 10. Тема: Функция y = x2 Математическое исследование
- 11. Постройте
- 12. Алгоритм построения параболы.. 1.Заполнить таблицу значений
- 13. Перевал Парабола Невероятно, но факт!
- 14. Траектория камня, брошенного под углом
- 15. Свойства функции y = x2
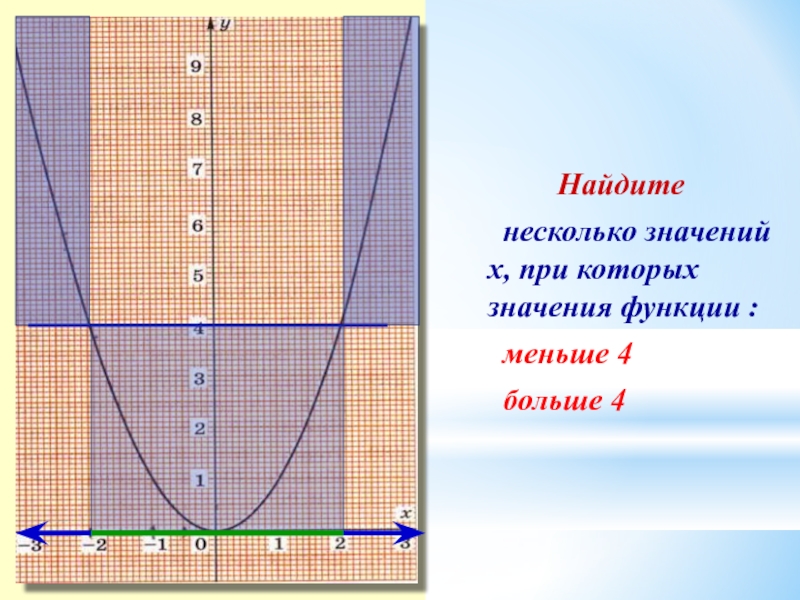
- 16. Область определения функции
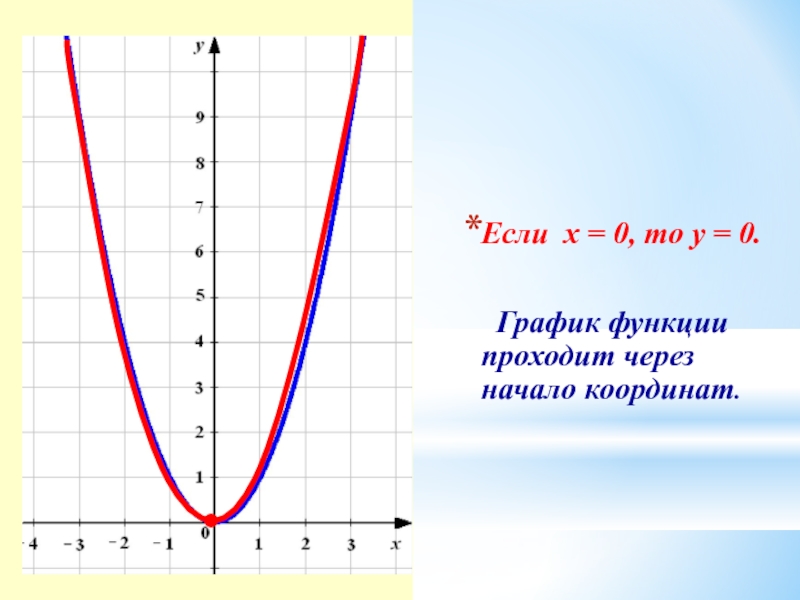
- 17. Если х = 0, то
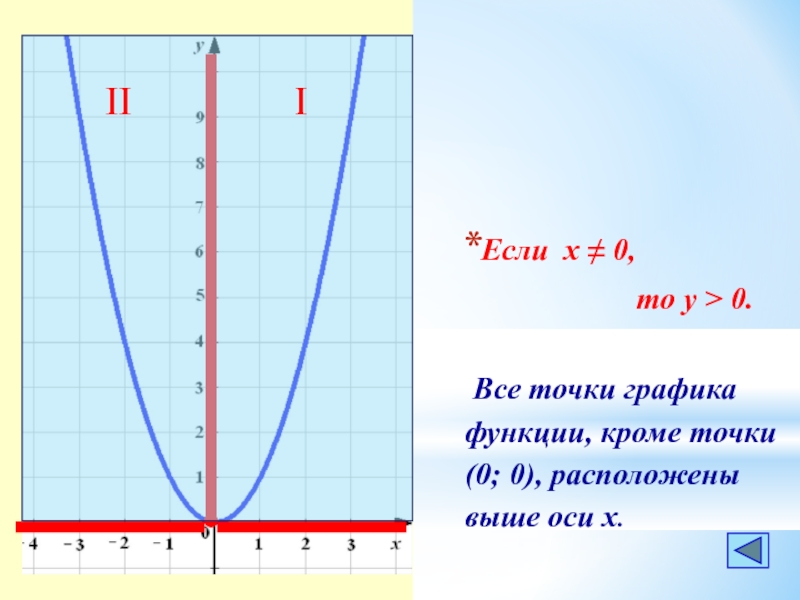
- 18. Если х ≠ 0,
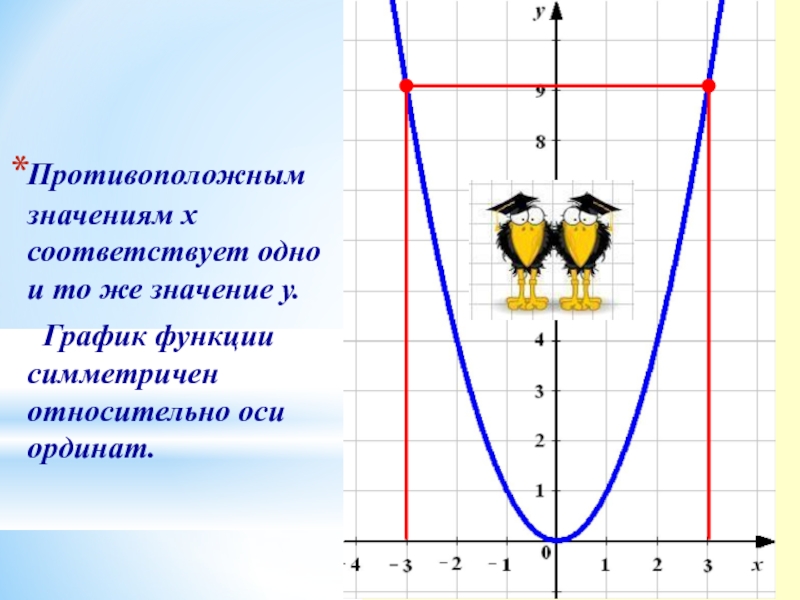
- 19. Противоположным значениям х соответствует одно
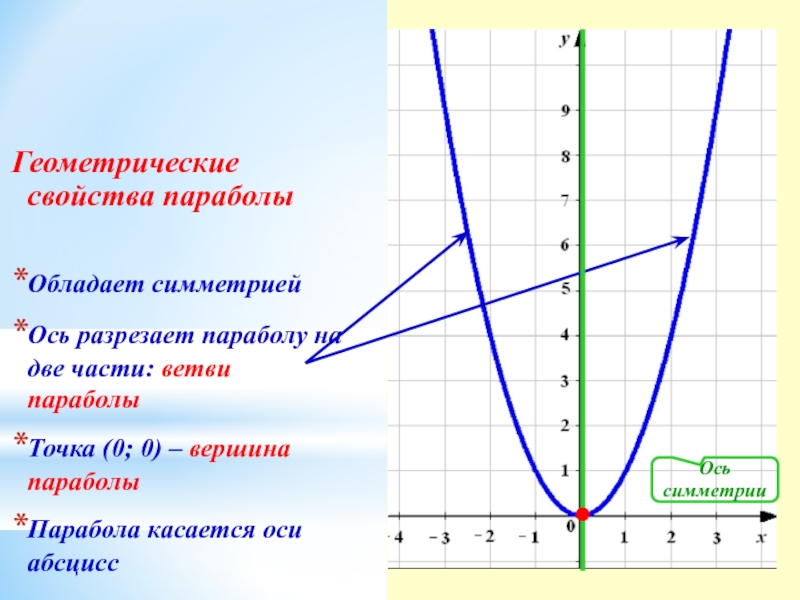
- 20. Геометрические свойства параболы Обладает симметрией
- 21. «Знание – орудие,
- 22. постройте в одной системе координат
- 24. При каких значениях а точка Р(а; 64)
- 25. Алгоритм решения уравнения графическим способом 1.
- 26. Удачи вам!
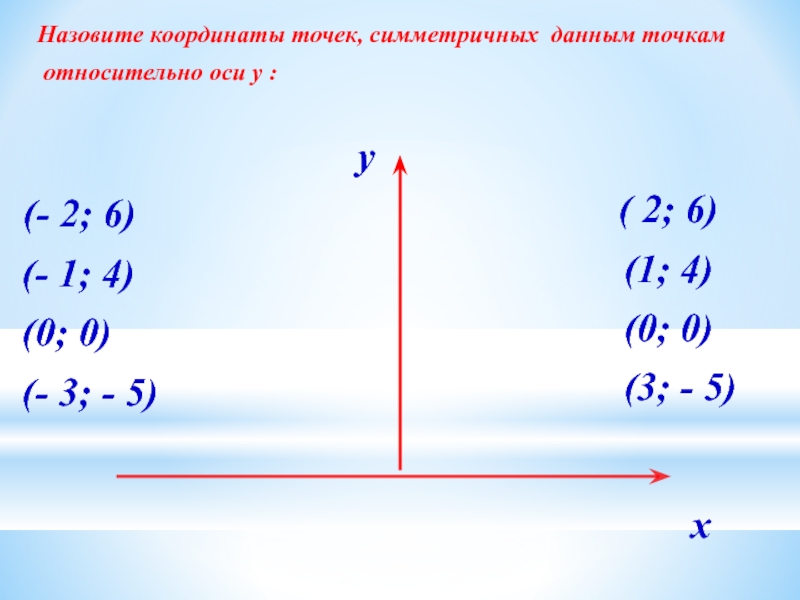
Слайд 2 Назовите координаты точек, симметричных данным точкам относительно оси y :
(- 1; 4)
(0; 0)
(- 3; - 5)
( 2; 6)
(1; 4)
(0; 0)
(3; - 5)
y
х
Слайд 4 На графике видно, что ось OY делит параболу на симметричные левую и
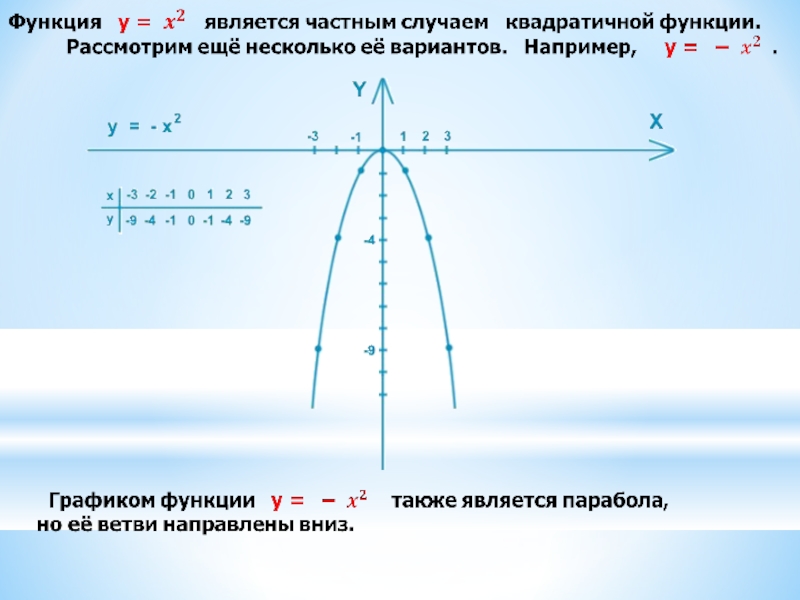
Слайд 6График функции y = x 2 + 3 — такая же парабола, но
Слайд 12Алгоритм построения параболы..
1.Заполнить таблицу значений Х и У.
2.Отметить в координатной плоскости
3.Соедините эти точки плавной линией.
Слайд 14 Траектория камня, брошенного под углом к горизонту, будет лететь
Знаете ли вы?
Слайд 16
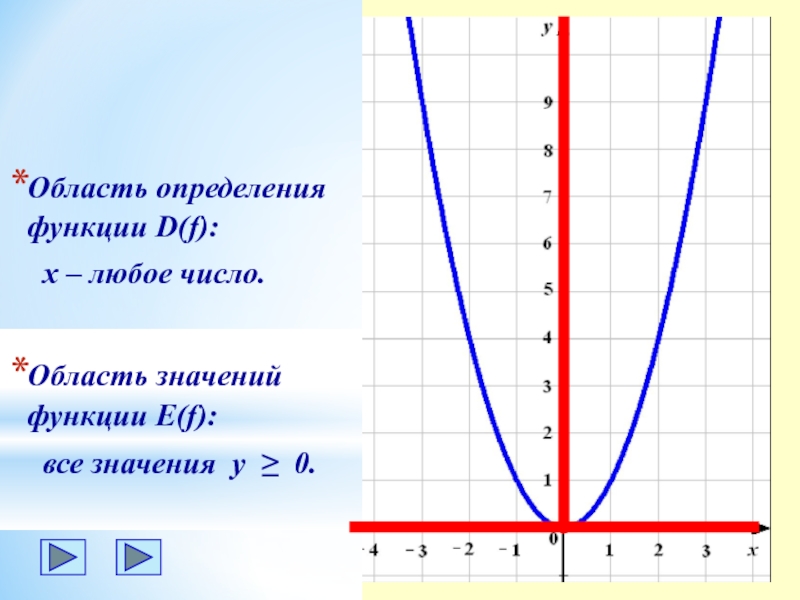
Область определения функции D(f):
х – любое число.
Область значений
все значения у ≥ 0.
Слайд 18
Если х ≠ 0,
Все точки графика
функции, кроме точки
(0; 0), расположены
выше оси х.
I
II
Слайд 19
Противоположным значениям х соответствует одно и то же значение у.
Слайд 20
Геометрические свойства параболы
Обладает симметрией
Ось разрезает параболу на две части: ветви параболы
Точка
Парабола касается оси абсцисс
Ось симметрии
Слайд 21«Знание – орудие,
Л. Н. Толстой
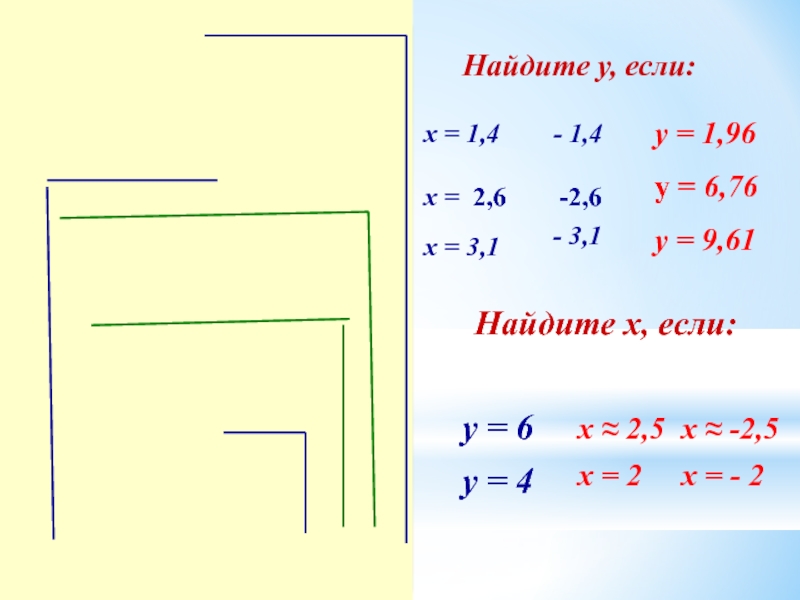
Найдите у, если:
х = 1,4
х = 2,6 -2,6
х = 3,1
у = 6
у = 4
Найдите х, если:
- 1,4
- 3,1
х ≈ -2,5
х = - 2
у = 1,96
у = 6,76
у = 9,61
х ≈ 2,5
х = 2
Слайд 22
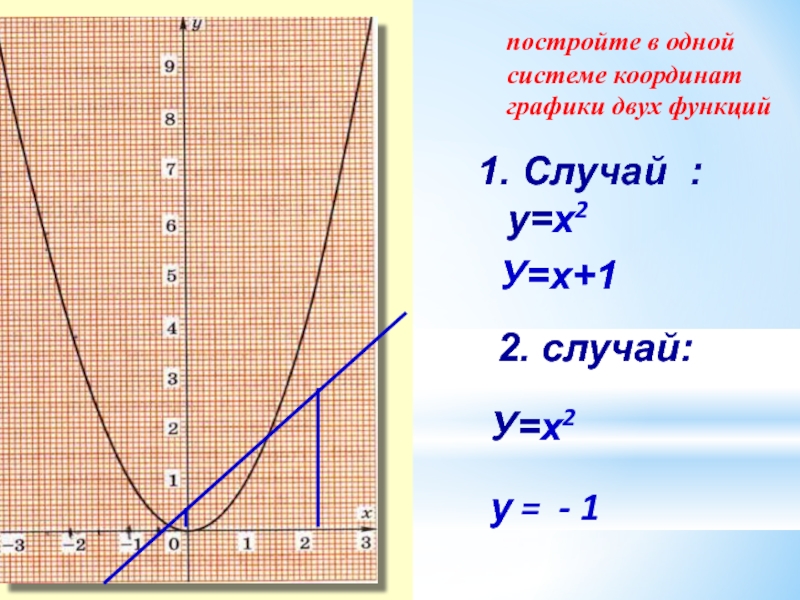
постройте в одной системе координат графики двух функций
1. Случай : у=х2
У=х+1
2. случай:
У=х2
у = - 1
Слайд 24При каких значениях а точка Р(а; 64) принадлежит графику функции у
Принадлежит ли графику функции у = х2 точка:
Не выполняя вычислений, определите, какие из точек не принадлежат графику функции у = х2:
P(-18; 324)
R(-99; -9081)
S(17; 279)
(-1; 1)
(0; 8)
(-2; 4)
(3; -9)
(1,8; 3,24)
(16; 0)
а = 8; а = - 8
принадлежит
не принадлежит
не принадлежит
Слайд 25Алгоритм решения уравнения графическим способом
1. Построить в одной системе координат
2. Найти абсциссы точек пересечения графиков. Это и будут корни уравнения.
3. Если точек пересечения нет, значит, уравнение не имеет корней