- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формализованное представление ЭА при автоматизированном проектировании презентация
Содержание
- 1. Формализованное представление ЭА при автоматизированном проектировании
- 3. 1. Матрица смежности Если задан граф G(X,
- 4. 1. Матрица смежности. Пример
- 5. 2. Матрица весовых соотношений строятся аналогично матрицам
- 6. 3. Матрица длин Это квадратная матрица (Lij – длина ребра):
- 7. 4. Матрица инцидентности Представляет собой прямоугольную матрицу.
- 8. 4. Матрица инцидентности. Пример
- 9. 5. Матрица смежности ребер Эта матрица, элементы которой образуются по правилу
- 10. 5. Матрица смежности ребер. Пример
- 12. Любую схему можно представить как некоторое подмножество
- 13. Электрическую схему задают также в виде матрицы
- 14. Тогда любую схему можно задать в виде
- 15. Граф вида G задается обычно в виде
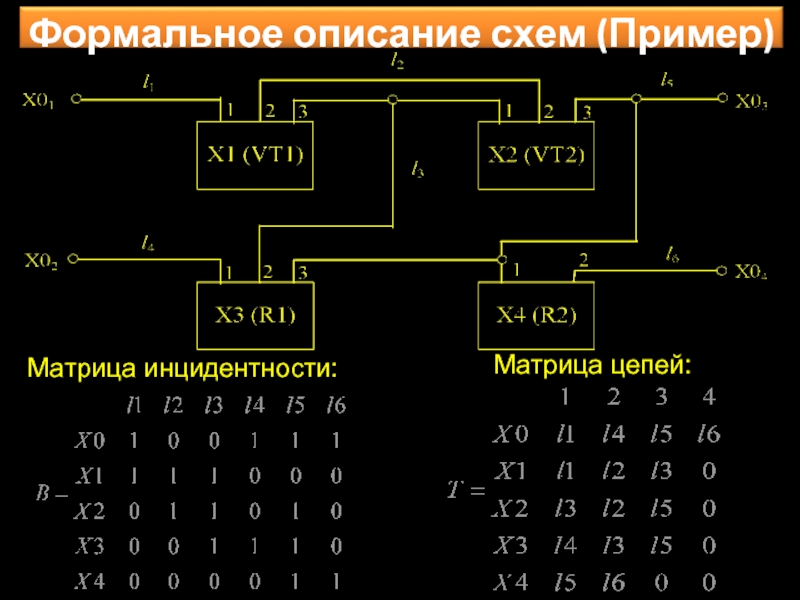
- 17. Матрица инцидентности: Матрица цепей:
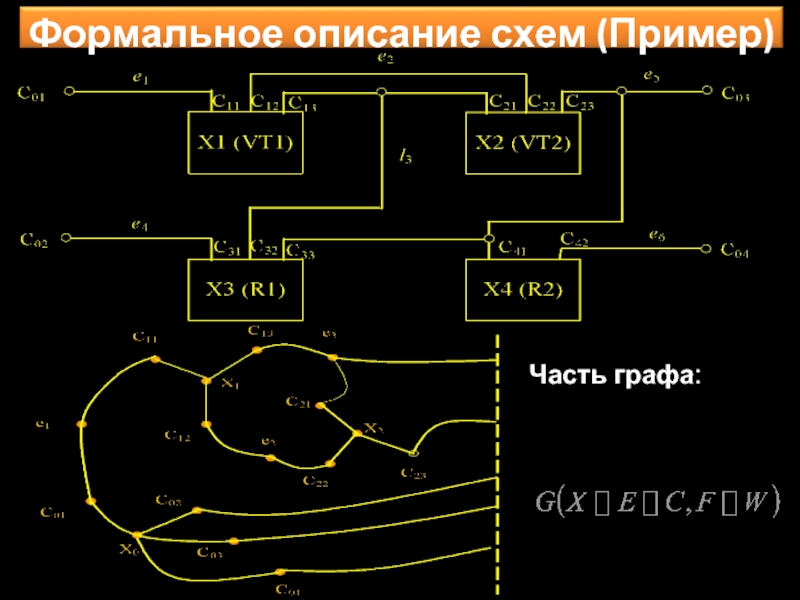
- 18. Часть графа:
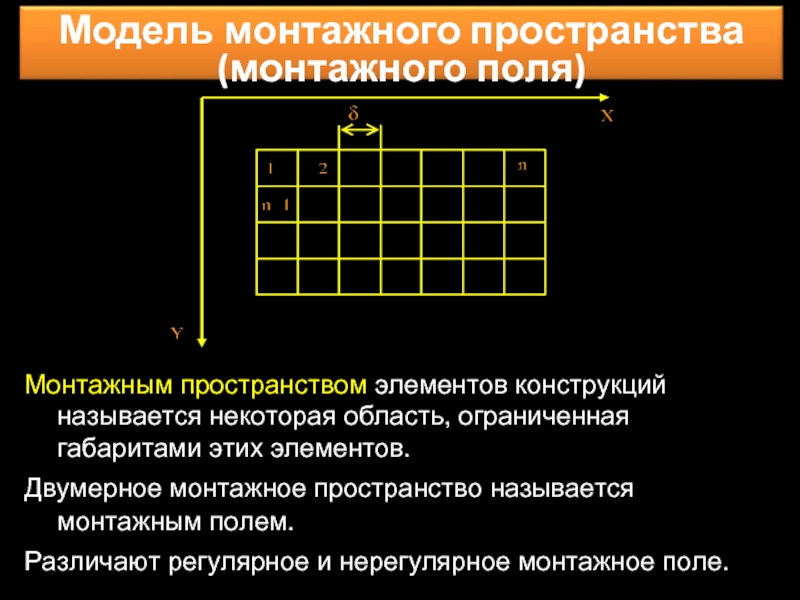
- 21. Монтажным пространством элементов конструкций называется некоторая область,
- 22. Минимальный размер ячейки где h – ширина
- 23. Машинный эквивалент дискретного монтажного поля - двумерный
- 24. Аналогично можно поставить в соответствие каждой ячейке
- 25. Вопросы по прочитанному материалу?
- 26. Спасибо за внимание!
Слайд 11 Описание графов с помощью матриц
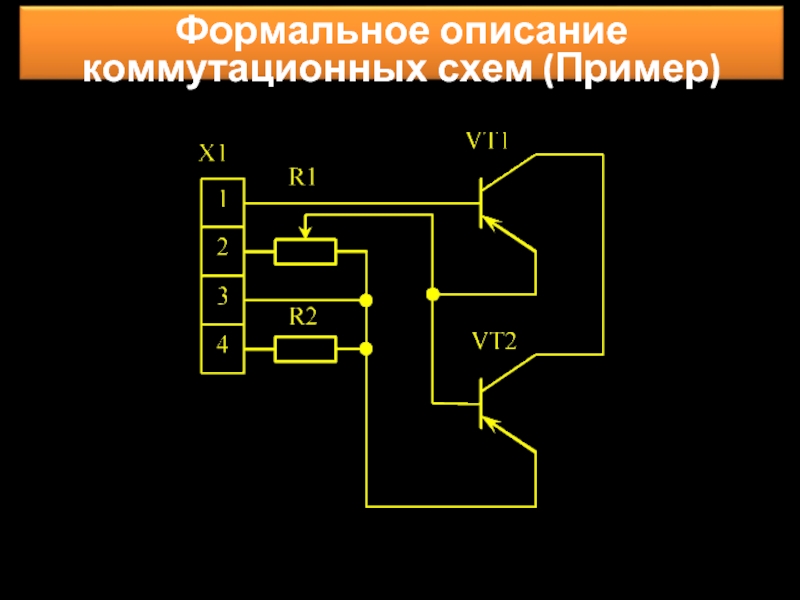
2 Формальное описание коммутационных схем
3 Основная
Слайд 31. Матрица смежности
Если задан граф G(X, U), то ему можно поставить
Слайд 52. Матрица весовых соотношений
строятся аналогично матрицам смежности, но значения их элементов
Слайд 74. Матрица инцидентности
Представляет собой прямоугольную матрицу. Строки матрицы соответствуют вершинам, а
Слайд 12Любую схему можно представить как некоторое подмножество элементов XL:
соединенных между собой
Представляя гиперграф H (X, E) матрицей инцидентности B получаем удобную форму представления схемы в памяти компьютера.
Слайд 13Электрическую схему задают также в виде матрицы цепей:
Каждый элемент схемы имеет
Слайд 14Тогда любую схему можно задать в виде графа:
F – определяет принадлежность
W - задаются вхождением контакта из множества С в цепи Е.
Слайд 15Граф вида G задается обычно в виде трехмерной матрицы А, которую
Слайд 21Монтажным пространством элементов конструкций называется некоторая область, ограниченная габаритами этих элементов.
Двумерное
Различают регулярное и нерегулярное монтажное поле.
Слайд 22Минимальный размер ячейки
где h – ширина проводника, s – минимальное расстояние
Общее число дискретных ячеек:
Место любого i-го дискрета на монтажном поле однозначно может быть указано его координатами (xi, yi) в системе дискретных координат, либо индексом I
дискрет → код
Слайд 23Машинный эквивалент дискретного монтажного поля - двумерный массив B (X,Y), значения
либо одномерный массив B(I).
→ 0 ⇒ возрастает класс точности ПП
Слайд 24Аналогично можно поставить в соответствие каждой ячейке вершину графа, тогда модель
Модель монтажного пространства описывается также матрицей расстояний (Lij – длина ребра):