гипотез
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы теории вероятностей и статистики. Решение задач на проверку статистических гипотез презентация
Содержание
- 1. Элементы теории вероятностей и статистики. Решение задач на проверку статистических гипотез
- 2. 1) 2) I)
- 4. II) III)
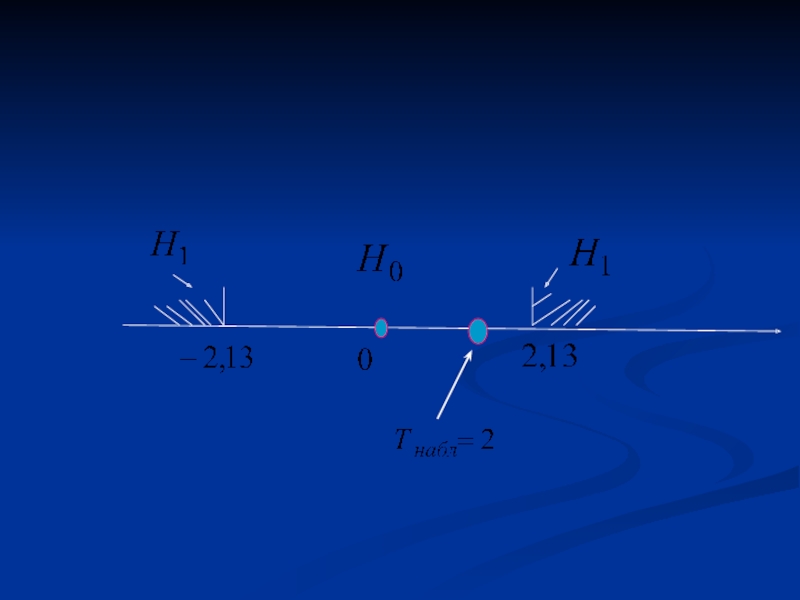
- 5. Задача №1 Проверить гипотезы: Решение: 1.
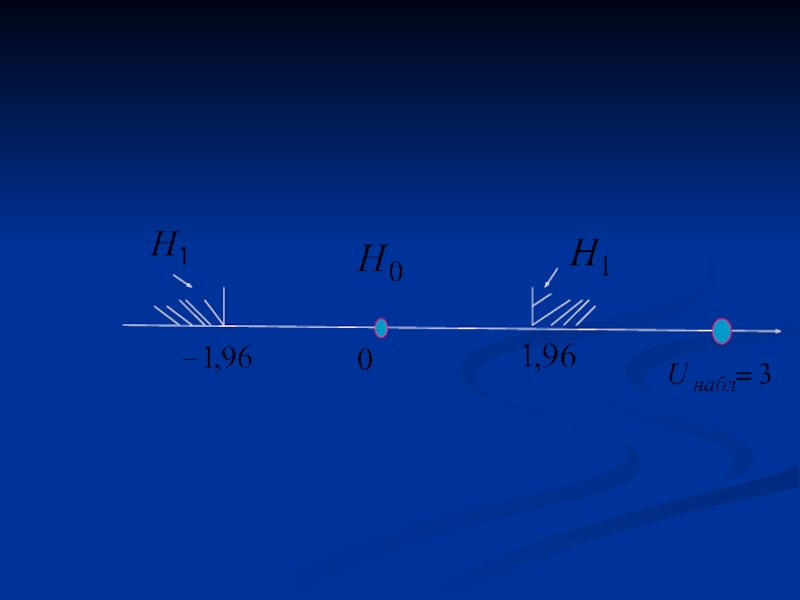
- 7. Задача №1 3. Принятие решения
- 10. Задача №1 5. Принятие решения
- 12. 7. Принятие решения
- 13. Проверка гипотезы о мат. ожидании нормальной СВ при неизвестной дисперсии 1) 2) 3)
- 14. 4) Проверка гипотезы о мат. ожидании нормальной СВ при неизвестной дисперсии 5)
- 15. Задача №2 Проверить гипотезы: Решение: 1.
- 17. 3. Принятие решения
- 20. 5. Принятие решения
- 21. Проверка гипотезы о величине дисперсии нормальной СВ
- 22. Проверка гипотезы о величине дисперсии нормальной СВ
- 23. Проверка гипотезы о величине дисперсии нормальной СВ
- 24. Проверка гипотезы о величине дисперсии нормальной СВ 5)
- 25. Задача №3 Проверить гипотезы: Решение: 1.
- 27. 3. Принятие решения
- 28. Проверка гипотезы о равенстве мат. ожиданий двух нормальных СВ (известные дисперсии) 3) 2) 1)
- 29. Проверка гипотезы о равенстве мат. ожиданий двух нормальных СВ (известные дисперсии) 4)
- 30. Проверка гипотезы о равенстве мат. ожиданий двух нормальных СВ (известные дисперсии) 5)
- 31. Проверка гипотезы о равенстве мат. ожиданий двух нормальных СВ (известные дисперсии) 5)
- 32. Задача №4 Проверить гипотезу: Решение: 1. Вычисляем
- 34. 3. Принятие решения
- 35. Проверка гипотезы о равенстве мат. ожиданий двух нормальных СВ (дисперсии неизвестны) 1) 2) 3)
- 36. Проверка гипотезы о равенстве мат. ожиданий двух нормальных СВ (дисперсии неизвестны) 4)
- 37. Проверка гипотезы о равенстве мат. ожиданий двух нормальных СВ (дисперсии неизвестны) 5)
- 38. Проверка гипотезы о равенстве мат. ожиданий двух нормальных СВ (дисперсии неизвестны) 6)
- 39. Задача №5 Решение: 1. Проводим правостороннюю роверку
- 41. 4. Принятие решения
- 42. Проверка гипотезы о равенстве дисперсий двух нормальных СВ (дисп. неизв.) 1) 2) 3)
- 43. Проверка гипотезы о равенстве дисперсий двух нормальных СВ 4)
- 44. Задача №6 Проверить гипотезы: Решение: 1.
- 46. 3. Принятие решения
Слайд 5
Задача №1
Проверить гипотезы:
Решение:
1. Вычисляем набл. значение стат. критерия
n=100, X~N(m,
5),
Слайд 15
Задача №2
Проверить гипотезы:
Решение:
1. Вычисляем набл. значение стат. критерия
n=16, X~N(m,
σ),
Слайд 21Проверка гипотезы о величине дисперсии нормальной СВ
Проверка гипотезы о величине дисперсии
нормальной СВ
1)
2)
3)
Слайд 23Проверка гипотезы о величине дисперсии нормальной СВ
Проверка гипотезы о величине дисперсии
нормальной СВ
Проверка гипотезы о величине дисперсии нормальной СВ
Проверка гипотезы о величине дисперсии нормальной СВ
4)
Слайд 25
Задача №3
Проверить гипотезы:
Решение:
1. Вычисляем набл. значение стат. критерия
N=25, X~N(m,
σ),
Слайд 39Задача №5
Решение:
1. Проводим правостороннюю роверку
n=10, k=16
2. Вычисляем набл.
значение стат. критерия