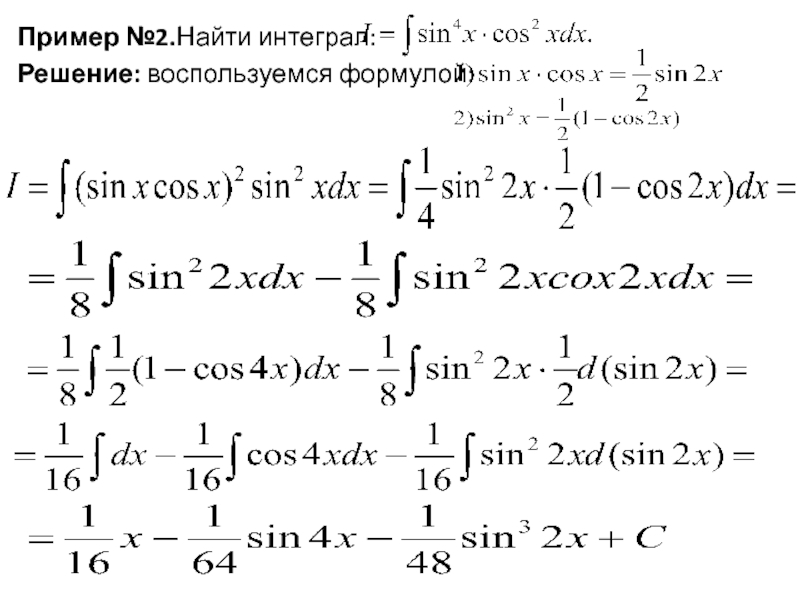интегралами от квадратичных иррациональностей.Их можно найти следующим образом: под радикалом выделить полный квадрат:
и сделать подстановку
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интегрирование иррациональных функций презентация
Содержание
- 1. Интегрирование иррациональных функций
- 2. При этом первые два интеграла приводятся к
- 3. Пример №2.Найти интеграл : Решение:
- 4. Интегрирование тригонометрических функций Интегралы вида Находятся с помощью формул:
- 5. Пример №1. Найти интеграл: Решение:Воспользуемся формулой Получим: Тогда
- 6. Пример№2.
- 7. Пример№3. Найти интеграл: Решение:
- 8. Интегралы типа Для
- 9. Пример№1. Найти интеграл: Решение: Применим
- 10. Пример №2.Найти интеграл: Решение: воспользуемся формулой:
- 11. Пример №3.
- 12. Универсальная тригонометрическая подстановка Рассмотрим некоторые случаи нахождения
- 13. Действительно,
- 14. На практике применяют
- 15. Пример: Найти интеграл Решение: Сделаем универсальную
Слайд 1Интегрирование иррациональных функций
Квадратичные иррациональности
Рассмотрим некоторые типы интегралов,содержащих иррациональные функции.
Интегралы типа
Называют неопределенными
Слайд 2При этом первые два интеграла приводятся к табличным, а третий –
к сумме двух табличных интегралов.
Пример№1. Найти интеграл:
Решение: Так как
Пример№1. Найти интеграл:
Решение: Так как
Слайд 8 Интегралы типа
Для нахождения таких интегралов используются следующие
приемы:
Подстановка если целое положительное нечетное число;
Подстановка если целое положительное нечетное число;
Формулы понижения порядка:
Если целые неотрицательные четные числа;
4)Подстановка если есть четное отрицательное целое число.
Подстановка если целое положительное нечетное число;
Подстановка если целое положительное нечетное число;
Формулы понижения порядка:
Если целые неотрицательные четные числа;
4)Подстановка если есть четное отрицательное целое число.
Слайд 12Универсальная тригонометрическая подстановка
Рассмотрим некоторые случаи нахождения интеграла от тригонометрическихфункций.Функцию с переменными
и ,над которыми выполняются рациональные действия (сложения,вычитание,умножение иделение)
Принято обозначать знак рациональной функции.
Вычисление неопределённых интегралов типа
Сводится к вычислению интегралов от рациональной функции подстановкой ,которая называется универсальной
Принято обозначать знак рациональной функции.
Вычисление неопределённых интегралов типа
Сводится к вычислению интегралов от рациональной функции подстановкой ,которая называется универсальной
Слайд 13Действительно,
Поэтому
Где рациональная функция
от .Обычно этот способ весьма громоздкий,зато всегда приводит к результату.
Слайд 14
На практике применяют и другие,более простые подстановки,
в зависимости
от свойств ( и вида) подынтегральной функции.В частности,удобны следующие правила:
1)Если функция нечётна относительно
Т.е ,то подстановка
рационализирует интеграл;
2)Если функция нечётна относительно
Т.е. ,то делается подстановка
3)Если функция четна относительно
,то интеграл рационализируется подстановкой .Такая же подстановка применяется,если интеграл имеет вид
1)Если функция нечётна относительно
Т.е ,то подстановка
рационализирует интеграл;
2)Если функция нечётна относительно
Т.е. ,то делается подстановка
3)Если функция четна относительно
,то интеграл рационализируется подстановкой .Такая же подстановка применяется,если интеграл имеет вид