- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи С4. Как находить высоты и биссектрисы треугольника презентация
Содержание
- 1. Задачи С4. Как находить высоты и биссектрисы треугольника
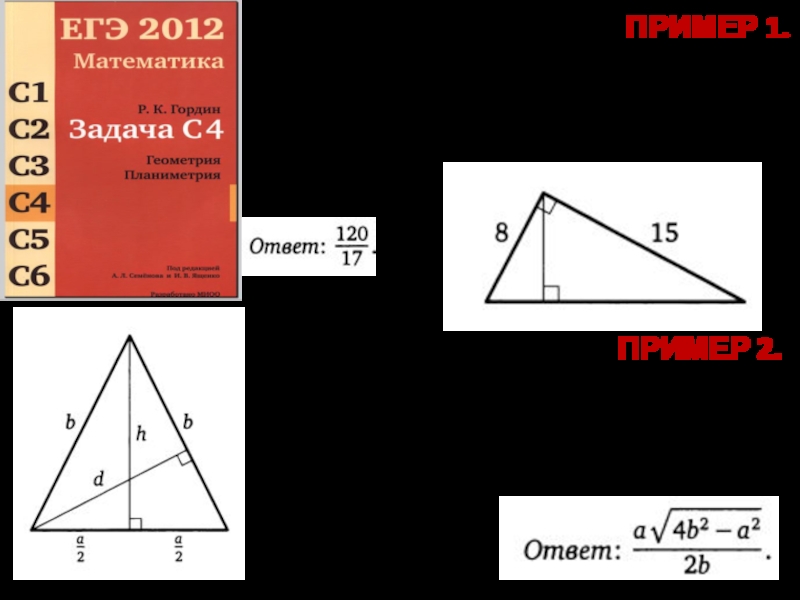
- 2. ПРИМЕР 1. Катеты прямоугольного треугольника равны
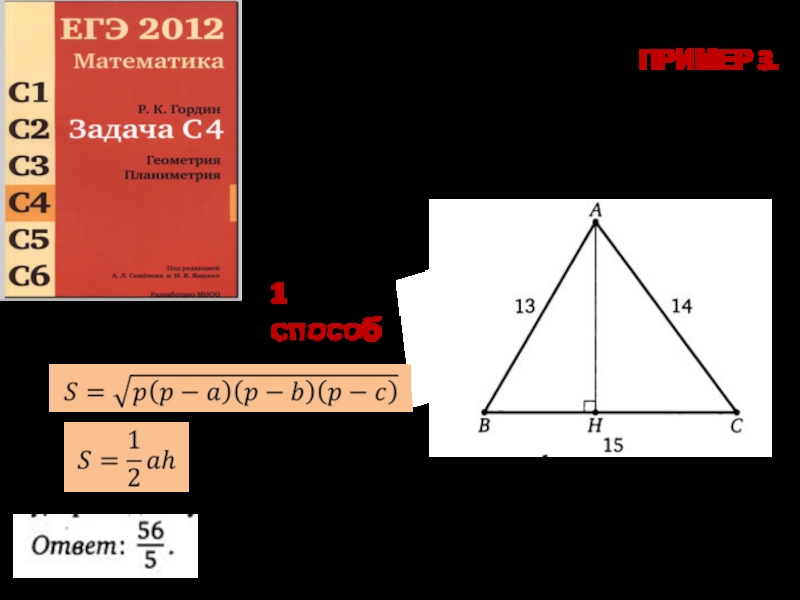
- 3. ПРИМЕР 3. Дан треугольник со сторонами 13,14,15.
- 4. ПРИМЕР 3. Дан треугольник со сторонами 13,14,15.
- 5. ПРИМЕР 3. Дан треугольник со сторонами 13,14,15.
- 6. Задача 5 из диагностической работы Две стороны
- 7. Задача 5 из диагностической работы Две стороны
- 8. Задача 5 из диагностической работы Две стороны
- 9. Задача 5 из диагностической работы Две стороны
- 10. Задача 5 из диагностической работы Две стороны
- 11. ПРИМЕР 4. Стороны треугольника
- 12. ПРИМЕР 5. Вычислите биссектрису треугольника ABC, проведённую
- 13. ПРИМЕР 5. Вычислите биссектрису треугольника ABC, проведённую
- 14. Утверждение. Квадрат биссектрисы треугольника равен произведению сторон,
- 15. ПРИМЕР 5. Вычислите биссектрису треугольника ABC, проведённую
- 16. 8 подготовительных задач 5.1. Катет и
- 17. 8 подготовительных задач 5.4. Стороны треугольника
- 18. 8 подготовительных задач 5.7. В треугольнике
Слайд 2ПРИМЕР 1. Катеты прямоугольного треугольника равны 15 и 8. Найдите высоту,
ПРИМЕР 2.
Дан треугольник со сторонами а, b и b. Найдите высоту, опущенную на сторону, равную Ь.
Слайд 3ПРИМЕР 3. Дан треугольник со сторонами 13,14,15. Найдите высоту, проведённую к большей
«площадной» подход
1 способ
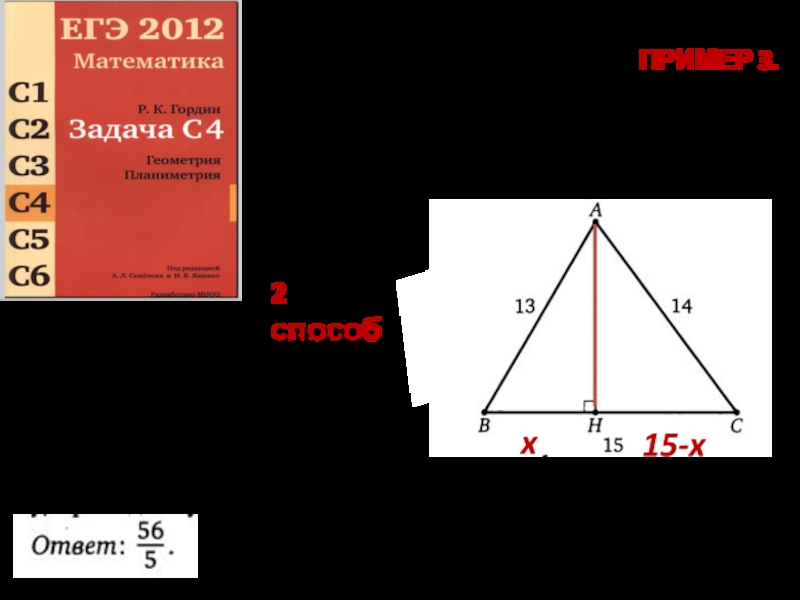
Слайд 4ПРИМЕР 3. Дан треугольник со сторонами 13,14,15. Найдите высоту, проведённую к большей
Уравнение на основе теоремы Пифагора
2 способ
x
15-x
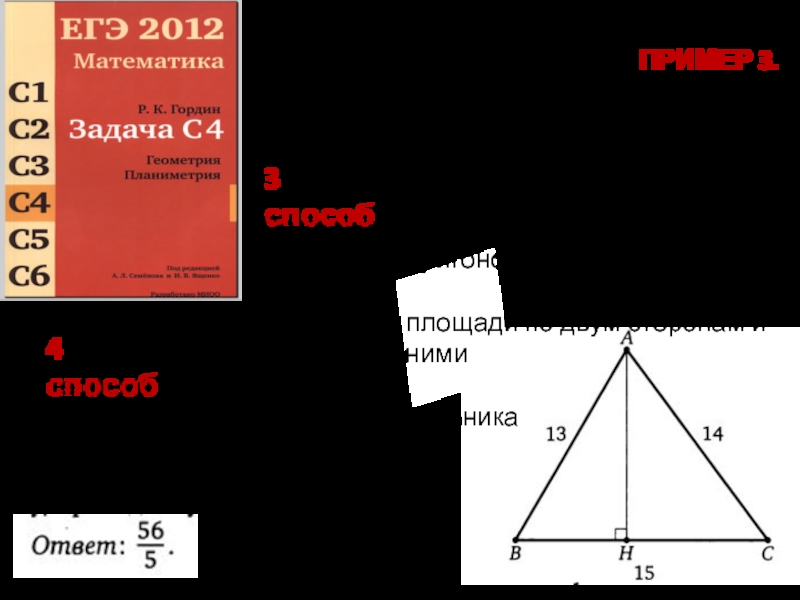
Слайд 5ПРИМЕР 3. Дан треугольник со сторонами 13,14,15. Найдите высоту, проведённую к большей
По теореме косинусов
+ основное тригонометрическое тождество
+ формула площади по двум сторонам и углу между ними
3 способ
По теореме косинусов
+ решение прямоугольного треугольника АВН
4 способ
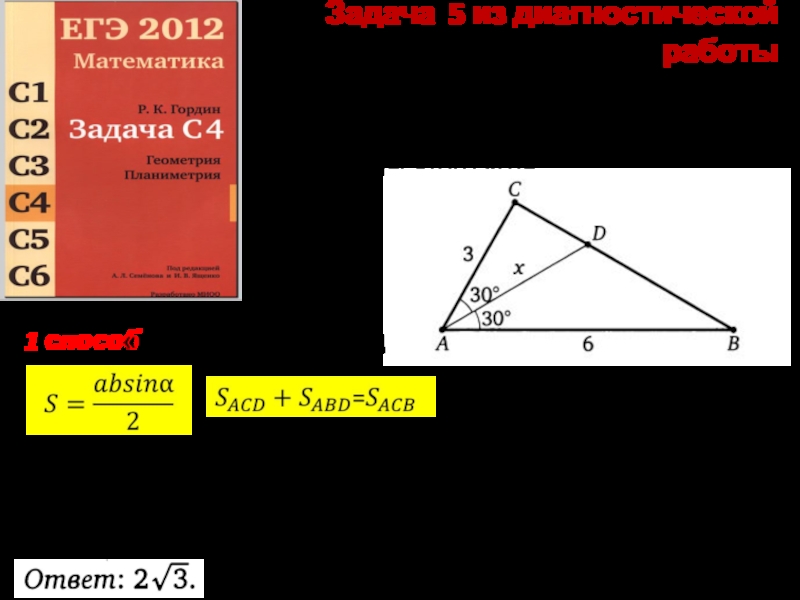
Слайд 6Задача 5 из диагностической работы
Две стороны треугольника равны 3 и 6,
1 способ
«площадной» подход
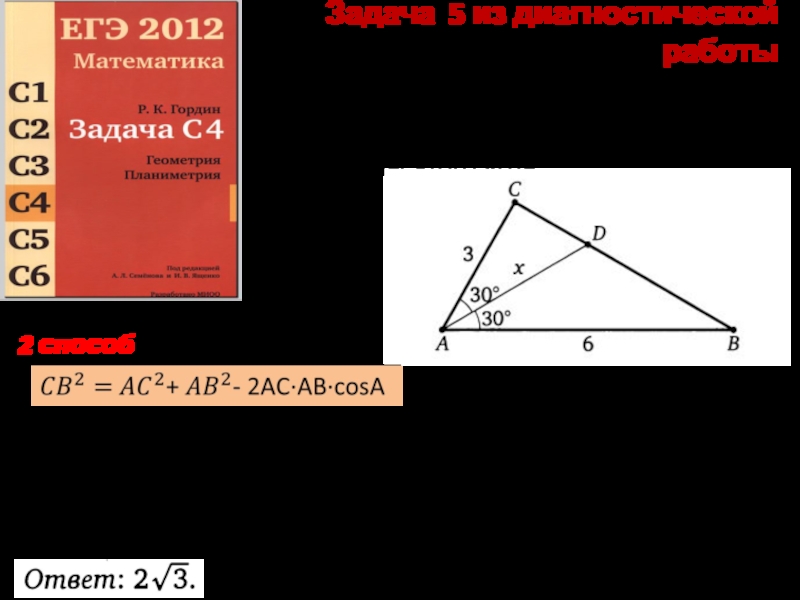
Слайд 7Задача 5 из диагностической работы
Две стороны треугольника равны 3 и 6,
∆ABC- прямоугольный => ∆ADC- прямоугольный
2 способ
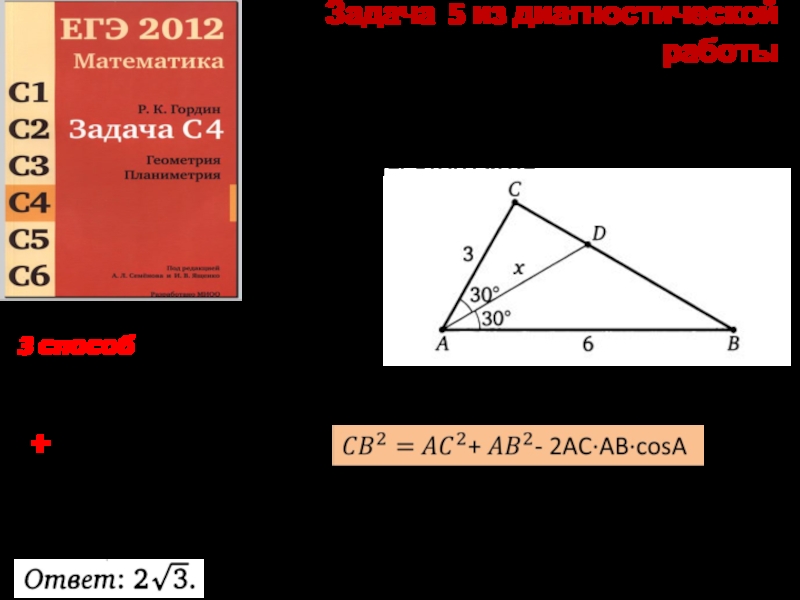
Слайд 8Задача 5 из диагностической работы
Две стороны треугольника равны 3 и 6,
CD:DB=AC:AB - свойство биссектрисы треугольника
+ теорема косинусов
3 способ
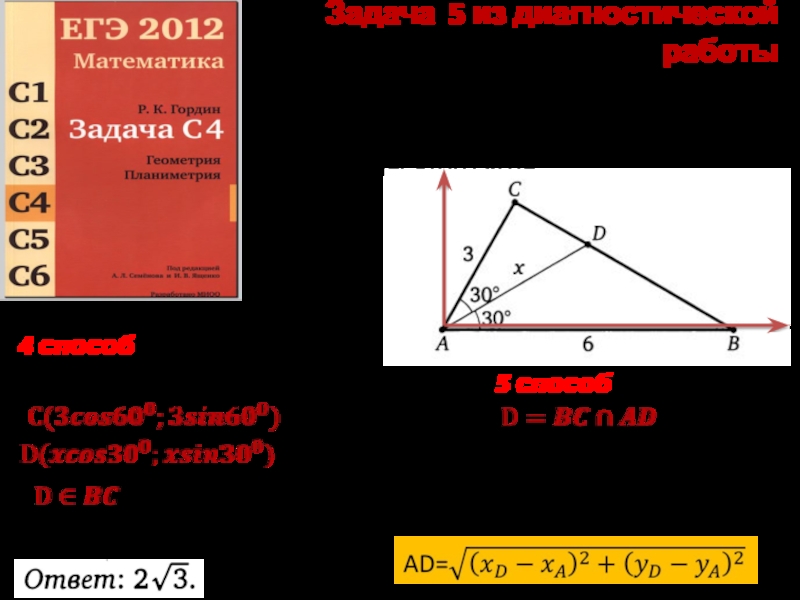
Слайд 9Задача 5 из диагностической работы
Две стороны треугольника равны 3 и 6,
Метод координат + уравнение прямой
4 способ
5 способ
Уравнение прямой ВС по координатам двух точек
Уравнение прямой AD по началу координат и угловому коэффициенту
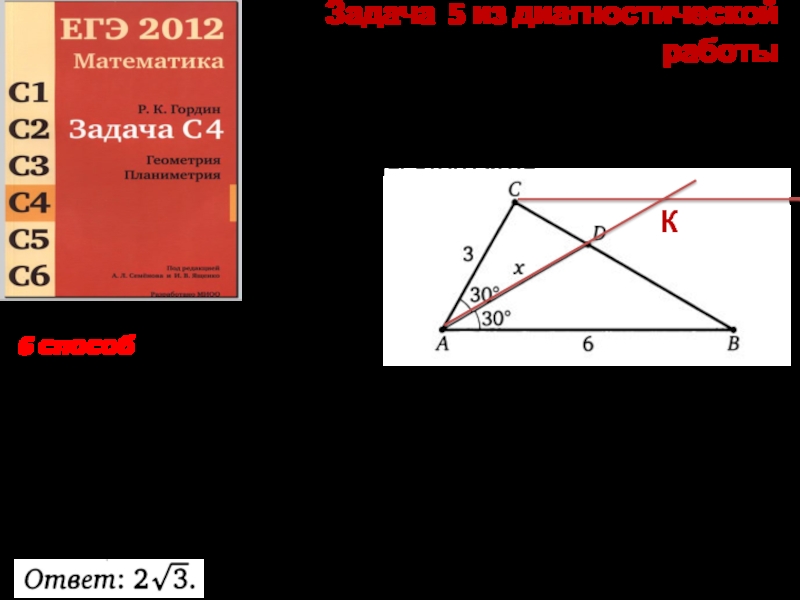
Слайд 10Задача 5 из диагностической работы
Две стороны треугольника равны 3 и 6,
дополнительные построения + подобие треугольников
6 способ
К
1. ∆ACK- равнобедренный => AK
2. ∆CDK~ ∆ADB, k=0,5 => AD
Слайд 11ПРИМЕР 4.
Стороны треугольника равны а и Ь, а угол
Слайд 12ПРИМЕР 5. Вычислите биссектрису треугольника ABC, проведённую из вершины А, если ВС
Ответ:
10
18
Свойство биссектрисы + теорема косинусов
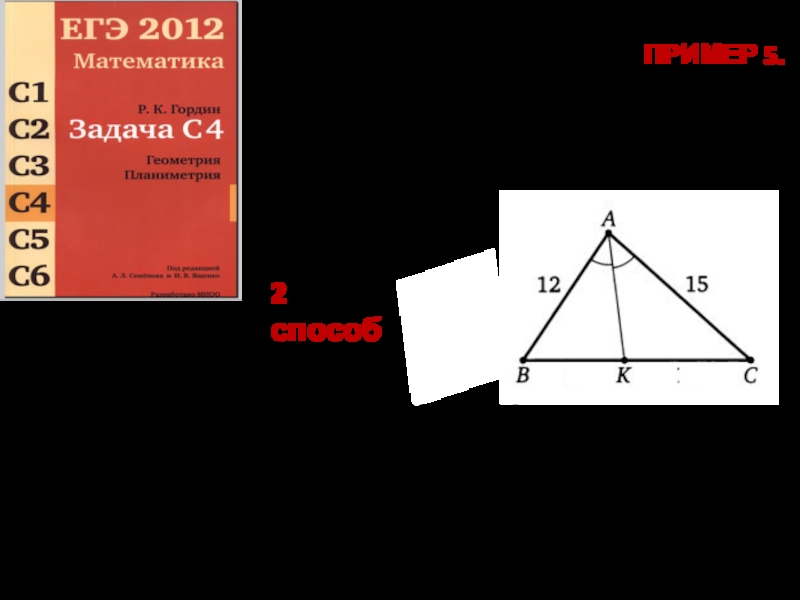
Слайд 13ПРИМЕР 5. Вычислите биссектрису треугольника ABC, проведённую из вершины А, если ВС
Ответ:
10
18
2 способ
по формуле для квадрата биссектрисы.
Утверждение. Квадрат биссектрисы треугольника равен произведению сторон, её заключающих, без произведения отрезков третьей стороны, на которые она разделена биссектрисой.
Слайд 14Утверждение. Квадрат биссектрисы треугольника равен произведению сторон, её заключающих, без произведения
Слайд 15ПРИМЕР 5. Вычислите биссектрису треугольника ABC, проведённую из вершины А, если ВС
Ответ:
10
18
ВК=12/27 от 18; BK= 8.
СК = ВС — ВК = 18 — 8 = 10.
По формуле для квадрата биссектрисы треугольника
находим, что
АК² =АВ·АС-ВК·СК= 12·15-8·10 = 180-80= 100.
2 способ
Слайд 168 подготовительных задач 5.1. Катет и гипотенуза прямоугольного треугольника равны 12 и
Слайд 178 подготовительных задач 5.4. Стороны треугольника равны 10,17 и 21. Найдите высоту
Слайд 188 подготовительных задач 5.7. В треугольнике ABC известно, что АВ = 8,
