- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Экономика как объект математического моделирования презентация
Содержание
- 1. Экономика как объект математического моделирования
- 2. ЛИТЕРАТУРА Васин А. А., Краснощеков П. С.,
- 3. В экономике действуют устойчивые количественные закономерности, поэтому возможно их формализованное математическое описание.
- 4. Объект изучения учебной дисциплины — экономика и
- 5. Особенности экономики как объекта моделирования
- 6. Таким образом, для выработки правильных экономических решений
- 7. Что такое экономико-математическая модель? Это упрощенное формальное
- 8. Элементы моделирования Экономическая система: размещает ресурсы, производит
- 9. Этапы построения модели Формулируются предмет и цели
- 10. Для построения модели нужно определить экзогенные
- 11. Классы экономико-математических моделей По уровню обобщения Макроэкономические
- 12. Макромодели отражают функционирование и развитие
- 13. По уровню абстракции Теоретические – позволяют изучить
- 14. Прикладные – дают возможность оценить параметры функционирования
- 15. Модели равновесные и роста Равновесные – дескриптивные
- 16. Модели роста – предназначены для определения того
- 17. По учету фактора времени. Статические – описывают
- 18. По учету фактора случайности. Детерминированные –
- 19. Методы оптимизации Во всех сферах человеческой деятельности
- 20. Существует два принципа выбора ВОЛЕВОЙ и
- 21. Вариант, для которого принятый критерий является наилучшим,
- 22. Виды задач оптимизации В общем случае
- 23. Суть такой постановки заключается в следующем: необходимо
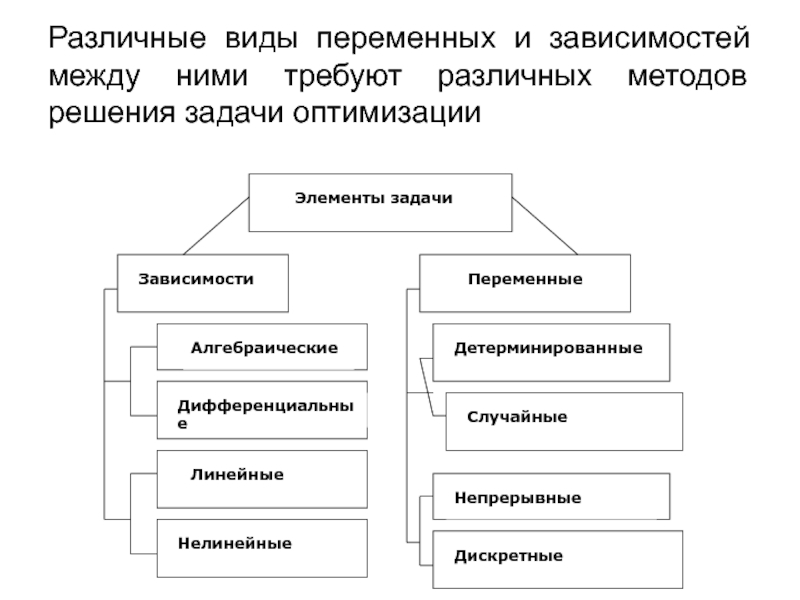
- 24. Различные виды переменных и зависимостей между ними требуют различных методов решения задачи оптимизации
- 25. Зависимости между переменными входят в ограничения и
- 26. Линейными называются такие зависимости, в которых переменные
- 27. Переменные можно подразделить на непрерывные и дискретные,
- 28. Важным видом дискретных переменных являются булевы переменные,
- 29. Задачи оптимизации, в которых переменные могут быть
- 30. Задачи оптимизации, в которые входят случайные
Слайд 2ЛИТЕРАТУРА
Васин А. А., Краснощеков П. С., Морозов В. В. Исследование операций, учеб.
пособие для студентов вузов , 2008
Балдин К. В., Башлыков В. Н., Рокосуев А. В. Математические методы и модели в экономике. УчебникФлинта (базовая коллекция), 2011
Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: Издат. “ДИС”, 2000.
Вентцель Е.С. Исследование операций. Задачи, принципы, методология._ М.: Высш.шк., 2001._208 с.
Исследование операций в экономике. /Под ред. Н.Ш. Кремера. – М.: Банки и бирижи. Издат. Объединение ЮНИТИ, 1997.
Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. – М.: Высшая школа, 1976.
Монахов В.М., Беляева В.С., Краснер Н.Я. Методы оптимизации. – М.: Просвещение, 1978.
Шелобаев С.И. Математические методы и модели. – М.: ЮНИТИ, 2000.
Балдин К. В., Башлыков В. Н., Рокосуев А. В. Математические методы и модели в экономике. УчебникФлинта (базовая коллекция), 2011
Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: Издат. “ДИС”, 2000.
Вентцель Е.С. Исследование операций. Задачи, принципы, методология._ М.: Высш.шк., 2001._208 с.
Исследование операций в экономике. /Под ред. Н.Ш. Кремера. – М.: Банки и бирижи. Издат. Объединение ЮНИТИ, 1997.
Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. – М.: Высшая школа, 1976.
Монахов В.М., Беляева В.С., Краснер Н.Я. Методы оптимизации. – М.: Просвещение, 1978.
Шелобаев С.И. Математические методы и модели. – М.: ЮНИТИ, 2000.
Слайд 3В экономике действуют устойчивые количественные закономерности, поэтому возможно их формализованное математическое
описание.
Слайд 4Объект изучения учебной дисциплины — экономика и ее подразделения.
Предмет — математические
модели экономических объектов.
Метод— системный анализ экономики как сложной динамической системы.
Метод— системный анализ экономики как сложной динамической системы.
Слайд 5 Особенности экономики как объекта моделирования
В экономике невозможны модели подобные
техническим, т.к. нельзя построить точную копию, экономики и на этой копии отрабатывать варианты экономической политики.
В экономике ограничены возможности экспериментов, поскольку все ее части жестко взаимосвязаны друг с другом.
остается — прошлый опыт и математическое моделирование.
В экономике ограничены возможности экспериментов, поскольку все ее части жестко взаимосвязаны друг с другом.
остается — прошлый опыт и математическое моделирование.
Слайд 6Таким образом, для выработки правильных экономических решений необходим учет всего прошлого
опыта
и результатов, полученных в расчетах по математическим моделям.
и результатов, полученных в расчетах по математическим моделям.
Слайд 7Что такое экономико-математическая модель?
Это упрощенное формальное описание экономических явлений.
Математическая модель экономического
объекта это его отображение в виде совокупности уравнений, неравенств, логических отношений, графиков.
Модели позволяют выявить особенности функционирования экономического объекта и на этой основе предсказать поведение объекта в будущем при изменении параметров.
Модели позволяют выявить особенности функционирования экономического объекта и на этой основе предсказать поведение объекта в будущем при изменении параметров.
Слайд 8Элементы моделирования
Экономическая система: размещает ресурсы, производит продукцию, распределяет предметы потребления и
осуществляет накопление.
Надсистема национальной экономики — природа, мировая экономика и общество.
Главные подсистемы экономики — производственная и финансово-кредитная.
Надсистема национальной экономики — природа, мировая экономика и общество.
Главные подсистемы экономики — производственная и финансово-кредитная.
Слайд 9Этапы построения модели
Формулируются предмет и цели исследования.
В экономической системе выделяются структурные
или функциональные элементы, соответствующие данной цели.
Выявляются наиболее важные качественные характеристики этих элементов.
Словесно, качественно описываются взаимосвязи между элементами.
Вводятся символические обозначения для характеристик экономического объекта и формулируются взаимосвязи между ними
Выявляются наиболее важные качественные характеристики этих элементов.
Словесно, качественно описываются взаимосвязи между элементами.
Вводятся символические обозначения для характеристик экономического объекта и формулируются взаимосвязи между ними
Слайд 10
Для построения модели нужно определить экзогенные и эндогенные переменные и параметры.
Экзогенные переменные – задаются вне модели, т.е. известны к моменту расчетов.
Эндогенные переменные – определяются в ходе расчетов по модели.
Параметры – коэффициенты уравнений
Проводятся расчеты по модели и анализируются полученные результаты.
Слайд 11Классы экономико-математических моделей
По уровню обобщения
Макроэкономические – описывают экономику как единое целое,
связывают укрупненные показатели: ВВП, потребление, инвестиции, занятость…
Микроэкономические –описывают взаимодействие структурных и функциональных составляющих экономики.
Микроэкономические –описывают взаимодействие структурных и функциональных составляющих экономики.
Слайд 12
Макромодели отражают функционирование и развитие всей экономической системы или ее
достаточно крупных подсистем.
Микромодели — функционирование хозяйственных единиц и их объединений.
В макромоделях хозяйственные ячейки считаются неделимыми;
В микромоделях хозяйственная единица может рассматриваться как сложная система.
Микромодели — функционирование хозяйственных единиц и их объединений.
В макромоделях хозяйственные ячейки считаются неделимыми;
В микромоделях хозяйственная единица может рассматриваться как сложная система.
Слайд 13По уровню абстракции
Теоретические – позволяют изучить общие свойства экономики путем вывода
из формальных предпосылок.
Используются для изучения общих свойств экономики и ее элементов (модели спроса и предложения)
Используются для изучения общих свойств экономики и ее элементов (модели спроса и предложения)
Слайд 14Прикладные – дают возможность оценить параметры функционирования конкретного экономического объекта и
выработать рекомендации по принятию решений.
Используются для оценки параметров конкретных экономических объектов.
Сюда относятся эконометрические модели, применяющие методы математической статистики.
Используются для оценки параметров конкретных экономических объектов.
Сюда относятся эконометрические модели, применяющие методы математической статистики.
Слайд 15Модели равновесные и роста
Равновесные – дескриптивные (описательные) модели. Они описывают такое
сотояние экономики, когда результирующая всех сил, стремящихся вывести экономику из этого состояния равна нулю.
Пример - модель Леонтьева (затраты-выпуск),
Пример - модель Леонтьева (затраты-выпуск),
Слайд 16Модели роста – предназначены для определения того как должна развиваться экономика
при определенных критериях.
Пример – Модель Солоу, Самуэльсона-Хикса
Пример – Модель Солоу, Самуэльсона-Хикса
Слайд 17По учету фактора времени.
Статические – описывают состояние объекта в конкретный момент
или период времени.
Динамические – включают взаимосвязи переменных во времени. Обычно используют аппарат дифференциальных уравнения.
Динамические – включают взаимосвязи переменных во времени. Обычно используют аппарат дифференциальных уравнения.
Слайд 18По учету фактора случайности.
Детерминированные – предполагают жесткие функциональные связи между
переменными модели.
Стохастические – допускают случайные воздействия на показатели и используют теорию вероятностей и математическую статистику.
Стохастические – допускают случайные воздействия на показатели и используют теорию вероятностей и математическую статистику.
Слайд 19Методы оптимизации
Во всех сферах человеческой деятельности большое место занимает принятие решений.
Для этого необходимо выполнить 2 условия:
Должно быть не менее 2-х вариантов.
Определен принцип выбора варианта из числа возможных.
Слайд 20
Существует два принципа выбора ВОЛЕВОЙ и КРИТЕРИАЛЬНЫЙ
Волевой выбор используется при отсутствии
количественных мер оценки вариантов, он является единственно возможным.
Критериальный выбор заключается в том, что принимается некоторый критерий и сравниваются возможные варианты по этому критерию.
Критериальный выбор заключается в том, что принимается некоторый критерий и сравниваются возможные варианты по этому критерию.
Слайд 21Вариант, для которого принятый критерий является наилучшим, называется оптимальным, и решение
– также называется оптимальным.
Задача принятия наилучшего решения – задача оптимизации.
Критерий оптимизации называют целевой функцией
Задача принятия наилучшего решения – задача оптимизации.
Критерий оптимизации называют целевой функцией
Слайд 22 Виды задач оптимизации
В общем случае задача оптимизации может быть записана
следующим образом:
F=f(xj)→max (min);
gi(xj)≤bi(i=1,m); (1)
dj≤xj≤Dj (j=1,n)
Система (1) представляет собой общий случай математической постановки задачи оптимизации. Она включает целевую функцию F, ограничения gi(xj)≤bi, и граничные условия dj≤xj≤Dj
F=f(xj)→max (min);
gi(xj)≤bi(i=1,m); (1)
dj≤xj≤Dj (j=1,n)
Система (1) представляет собой общий случай математической постановки задачи оптимизации. Она включает целевую функцию F, ограничения gi(xj)≤bi, и граничные условия dj≤xj≤Dj
Слайд 23Суть такой постановки заключается в следующем: необходимо определить такие значения xj,
которые находясь в граничных условиях dj≤xj≤Dj удовлетворяли бы ограничениям gi(xj)≤bi и при этом придавали бы целевой функции F=f(xj) искомое оптимальное значение.
В каждом конкретном случае система (1) определяется видом переменных xj и зависимостей f(xj) и gi(xj).
В каждом конкретном случае система (1) определяется видом переменных xj и зависимостей f(xj) и gi(xj).
Слайд 24Различные виды переменных и зависимостей между ними требуют различных методов решения
задачи оптимизации
Слайд 25Зависимости между переменными входят в ограничения и в целевую функцию.
По
виду действий над переменными зависимости могут быть алгебраическими и дифференциальными.
Задачи, содержащие дифференциальные зависимости в функции времени, называются задачами оптимального управления или – динамической оптимизации.
Задачи, содержащие дифференциальные зависимости в функции времени, называются задачами оптимального управления или – динамической оптимизации.
Слайд 26Линейными называются такие зависимости, в которых переменные находятся в первой степени.
Задачи
оптимизации, содержащие линейные алгебраические зависимости в целевой функции и ограничениях, являются задачами Линейного программирования.
Если в задаче оптимизации есть хотя бы одно нелинейное ограничение или целевая функция представляют собой нелинейную зависимость, задача является задачей Нелинейного программирования.
Если в задаче оптимизации есть хотя бы одно нелинейное ограничение или целевая функция представляют собой нелинейную зависимость, задача является задачей Нелинейного программирования.
Слайд 27Переменные можно подразделить на непрерывные и дискретные, детерминированные и случайные.
Если
величины в заданном интервале граничных условий могут принимать любые промежуточные значения, они называются непрерывными.
Примером непрерывных переменных может служить производительность, стоимость и т.д.
Если переменные в заданном интервале могут принимать лишь определенные значения, они называются дискретными.
Примером непрерывных переменных может служить производительность, стоимость и т.д.
Если переменные в заданном интервале могут принимать лишь определенные значения, они называются дискретными.
Слайд 28Важным видом дискретных переменных являются булевы переменные, они могут принимать только
два значения 0 или1.
С помощью булевых переменных можно решать логические, комбинационные и ряд других специфических задач.
Дискретные переменные могут быть целочисленными (принимают только целые значения), например, диаметр трубы должен соответствовать ГОСТУ и быть равным одному из заданных размеров: 100, 150, 200, 250 мм и т.д.
С помощью булевых переменных можно решать логические, комбинационные и ряд других специфических задач.
Дискретные переменные могут быть целочисленными (принимают только целые значения), например, диаметр трубы должен соответствовать ГОСТУ и быть равным одному из заданных размеров: 100, 150, 200, 250 мм и т.д.
Слайд 29Задачи оптимизации, в которых переменные могут быть только дискретными, называют задачами
дискретного или целочисленного программирования (ЦП).
Если в задаче часть переменных должна быть целочисленной, а остальные могут принимать непрерывные значения, то такая задача называется задачей частично-целочисленного программирования (ЧЦП).
Если в задаче часть переменных должна быть целочисленной, а остальные могут принимать непрерывные значения, то такая задача называется задачей частично-целочисленного программирования (ЧЦП).
Слайд 30 Задачи оптимизации, в которые входят случайные величины, задачами стохастического программирования
(СТП).
Все рассмотренные классы задач относятся к задачам математического программирования.
Все рассмотренные классы задач относятся к задачам математического программирования.