- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Эконометрика. Элементы теории вероятностей и математической статистики. (Тема 1) презентация
Содержание
- 1. Эконометрика. Элементы теории вероятностей и математической статистики. (Тема 1)
- 2. Литература Эконометрика. Книга 1, Ч.1,2: учебник. /
- 3. Тема 1. Введение. Элементы теории вероятностей и
- 4. 1. Случайные величины и их числовые характеристики.
- 5. 1. Случайные величины и их числовые характеристики.
- 6. 1. Случайные величины и их числовые характеристики.
- 7. 2. Функция распределения случайной величины. Непрерывные случайные
- 8. 2. Функция распределения случайной величины. Непрерывные случайные
- 9. 2. Функция распределения случайной величины. Непрерывные случайные
- 10. 3. Некоторые распределения случайных величин.
- 11. 3. Некоторые распределения случайных величин. 1) Дискретная
- 12. 3. Некоторые распределения случайных величин. 3) Непрерывная
- 13. 4. Многомерные случайные величины. Условные законы распределения.
- 14. 4. Многомерные случайные величины. Условные законы распределения.
- 15. 4. Многомерные случайные величины. Условные законы распределения.
- 16. 5. Двумерный (n-мерный) нормальный закон распределения. Сл.
- 17. 6. Закон больших чисел и предельные теоремы.
- 18. 6. Закон больших чисел и предельные теоремы.
- 19. 7. Точечные и интервальные оценки параметров. Оценкой
- 20. 7. Точечные и интервальные оценки параметров. Оценка
- 21. 7. Точечные и интервальные оценки параметров. Пример
- 22. 8. Проверка (тестирование) статистических гипотез Последовательность тестирования
- 23. 8. Проверка (тестирование) статистических гипотез Критическая область
- 24. 8. Проверка (тестирование) статистических гипотез Поэтому критическую
- 25. Вопросы изученные в Теме 1: 32 Случайные
Слайд 2Литература
Эконометрика. Книга 1, Ч.1,2: учебник. / Носко В.П. — М.: Издательский
Эконометрика. Книга 2, Ч.3,4: учебник. / Носко В.П. — М.: Издательский дом «Дело» РАНХиГС, 2011. — 576 с. - [Электронный ресурс] – Режим доступа: http://www.twirpx.com/file/721946/
Эконометрика: учебник/ [К. В. Балдин и др.]; под ред. В. Б. Уткина. - 2-е изд. - М.: Дашков и К, 2011. - 562 с.
Эконометрика: учеб. для вузов по специальности "Математические методы в экономике" / В. А. Валентинов. - 2-е изд. - М. : Дашков и К°, 2010. - 445 с. - [Электронный ресурс] – Режим доступа: http://library.pgups.ru/
Эконометрика: Учебник. / Н. Ш. Кремер, Б. А. Путко — М.: ЮНИТИ-ДАНА — 3-е издание, перераб. и доп. — 2010. — 328 с. - [Электронный ресурс] – Режим доступа: http://www.twirpx.com/file/1482079/
Эконометрика: учеб. для вузов по спец. 080601 "Статистика" и другим междисциплинар. спец.: учеб./ ред.: И. И. Елисеева [и др.]. - М.: Проспект, 2010. - 288 с.
Гореева Н.М., Демидова Л.Н, Клизогуб Л.М. и др. Эконометрика в схемах и таблицах. Учебное пособие под ред. д-ра экон. наук, проф. С. А. Орехова. - М.: Эксмо, 2008 - 224с. - [Электронный ресурс] – Режим доступа: http://www.twirpx.com/file/240925/
Эконометрика: учеб. пособие/ А. Н. Мардас; ПГУПС. - СПб.: ПГУПС, 2007. - 176 с.
Слайд 3Тема 1. Введение. Элементы теории вероятностей и математической статистики.
Случайные величины и
Функция распределения случайной величины. Непрерывные случайные величины.
Некоторые распределения случайных величин.
Многомерные случайные величины. Условные законы распределения.
Двумерный (n-мерный) нормальный закон распределения.
Закон больших чисел и предельные теоремы.
Точечные и интервальные оценки параметров.
Проверка (тестирование) статистических гипотез
Слайд 41. Случайные величины и их числовые характеристики.
Вероятность события А:
Р(А)= m/n,
где m - число случаев, благоприятствующих событию А, n - общее число случаев.
Статистическая вероятность Р*(А) - относительная частота (частость) W(А) появления события А в n произведенных испытаниях.
Cлучайная величина (сл. в.) - переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно - заранее не известно).
Дискретная сл. в.: множество возможных значений конечно или счетно (пример - число произведенных выстрелов до первого попадания).
Непрерывная сл. в.: множество возможных значений бесконечно и несчетно (пример - дальность полета артиллерийского снаряда).
Закон распределения сл. в. – всякое соотношение, устанавливающее связь между возможными значениями сл. в. xi и соответствующими им вероятностями pi.
Две случайные величины независимые, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина.
Слайд 51. Случайные величины и их числовые характеристики.
Закон распределения дискретной сл. в.:
при этом:
Числовые характеристики сл. в. - числа, в сжатой форме выражающие наиболее существенные черты распределения сл. в. (основные: математическое ожидание, дисперсия, среднее квадратическое отклонение).
Математическое ожидание (среднее значение) М(Х) дискретной сл. в. Х:
Слайд 61. Случайные величины и их числовые характеристики.
Дисперсия D(X) сл. в. Х
Для дискретной сл. в. Х:
Среднее квадратическое отклонение (стандартное отклонение или стандарт) сл. в. Х:
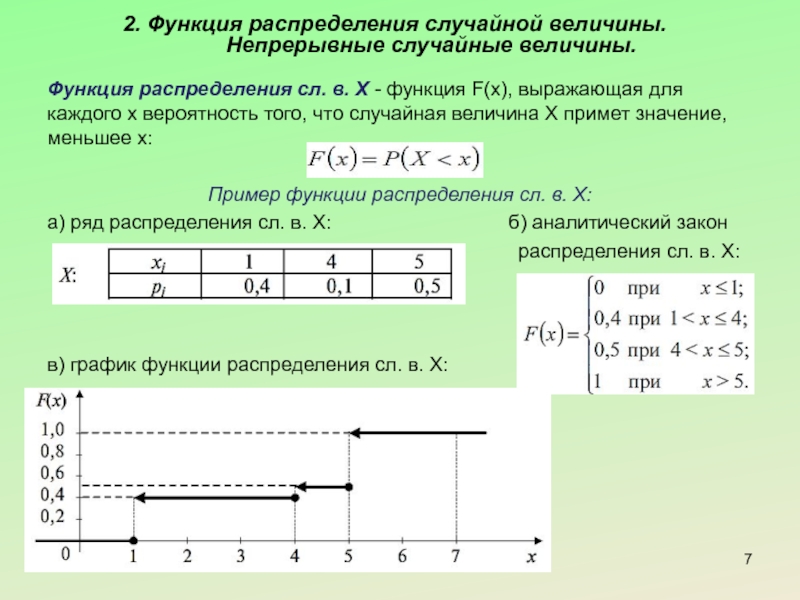
Слайд 72. Функция распределения случайной величины. Непрерывные случайные величины.
Функция распределения сл. в.
Пример функции распределения сл. в. X:
а) ряд распределения сл. в. X: б) аналитический закон
распределения сл. в. X:
в) график функции распределения сл. в. X:
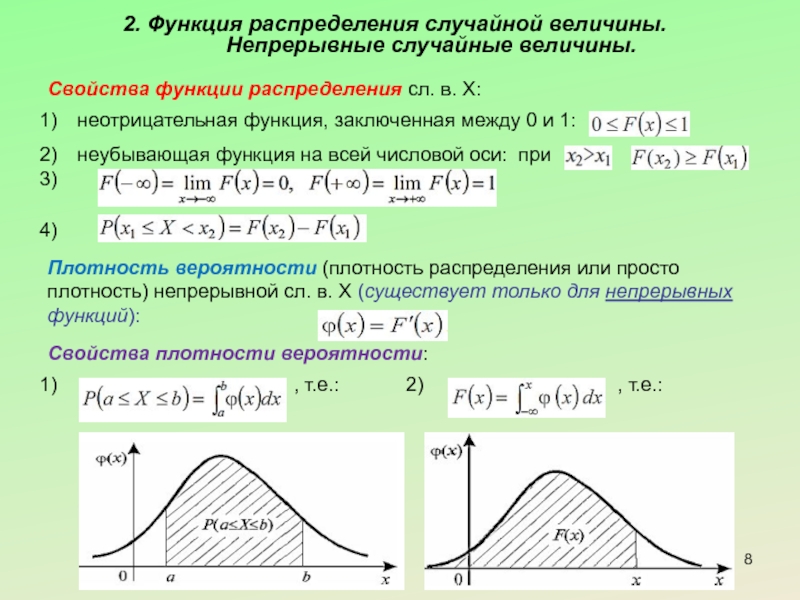
Слайд 82. Функция распределения случайной величины. Непрерывные случайные величины.
Свойства функции распределения сл.
неотрицательная функция, заключенная между 0 и 1:
неубывающая функция на всей числовой оси: при
Плотность вероятности (плотность распределения или просто плотность) непрерывной сл. в. X (существует только для непрерывных функций):
Свойства плотности вероятности:
, т.е.: 2) , т.е.:
Слайд 92. Функция распределения случайной величины. Непрерывные случайные величины.
3) неотрицательная функция:
Для непрерывной сл. в. Х:
(если интеграл абсолютно сходится);
или
(если интегралы сходятся)
Квантиль уровня q (q-квантиль) – такое значение xq сл. в., при котором функция ее распределения принимает значение, равное q, т. е.:
и q%-ая точка – это квантиль х1–q
Числовые характеристики сл. в.: начальные vk и центральные μk моменты k-го порядка для дискретных и непрерывных сл. в.:
( M(X) – начальный момент 1-го порядка, D(X) – центральный момент 2-го порядка )
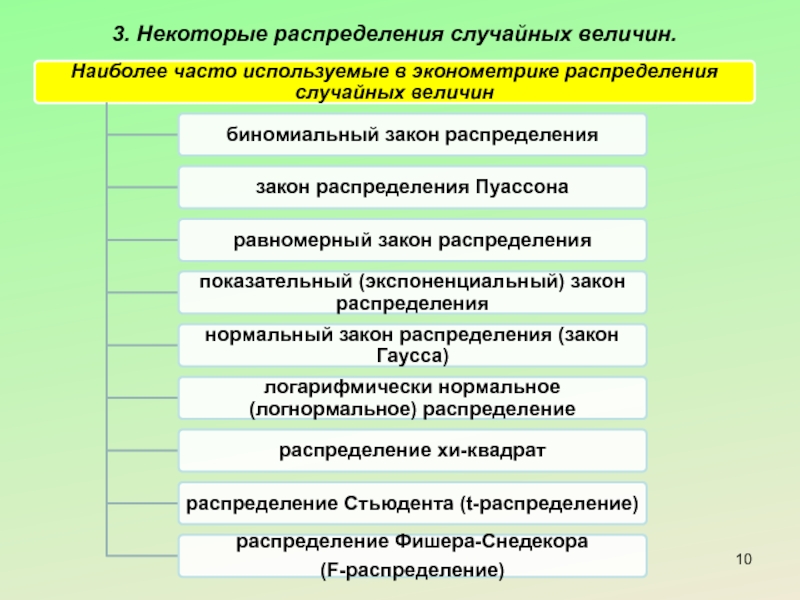
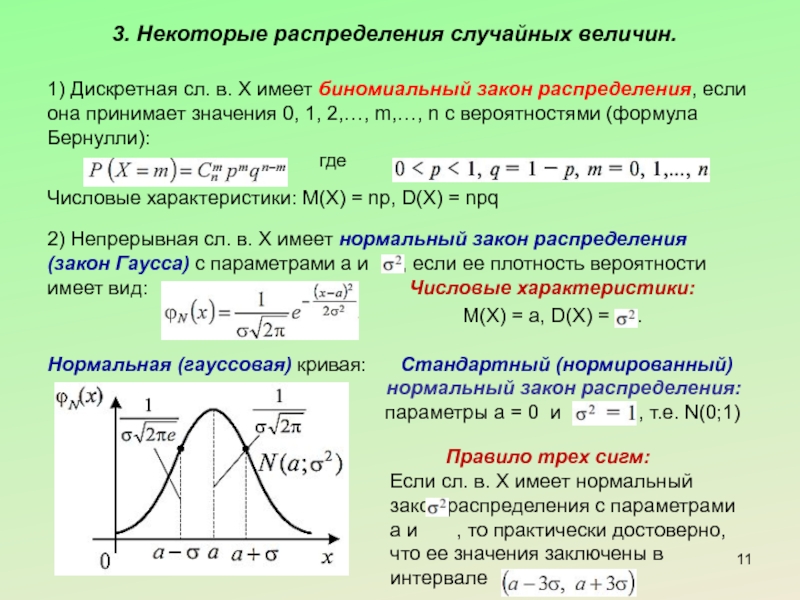
Слайд 113. Некоторые распределения случайных величин.
1) Дискретная сл. в. Х имеет биномиальный
где
Числовые характеристики: M(X) = np, D(X) = npq
2) Непрерывная сл. в. Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и , если ее плотность вероятности имеет вид: Числовые характеристики:
M(X) = a, D(X) = .
Нормальная (гауссовая) кривая: Стандартный (нормированный)
нормальный закон распределения:
параметры а = 0 и , т.е. N(0;1)
Правило трех сигм:
Если сл. в. Х имеет нормальный закон распределения с параметрами a и , то практически достоверно, что ее значения заключены в интервале
Слайд 123. Некоторые распределения случайных величин.
3) Непрерывная сл. в. Х имеет логарифмически
4) Распределение хи-квадрат с k степенями свободы - распределение суммы квадратов k независимых сл. в., распределенных по стандартному нормальному закону, т.е.:
5) Распределение Стьюдента (t-распределение) – распред-ие сл. в. t:
При t-распределение приближается к нормальному.
6) Распределение Фишера-Снедекора (F-распред.) – распред. сл. в. F:
Слайд 134. Многомерные случайные величины. Условные законы распределения.
Многомерная (n-мерная) сл. величина (система
(пример: многомерная случайная величина, характеризующая погоду в данном месте в определенное время суток: X1 – температура, X2 – скорость ветра, X3 – влажность, X4 - давление и т.д.).
Функция распределения n-мерной сл. величины (Х1,Х2,…, Xn) - функция F(x1,x2,…,xn), выражающая вероятность совместного выполнения n неравенств Х1
Для n=2 (двумерный случай):
Свойства F(x,y) аналогичны одномерному случаю F(x)
Плотность вероятности непрерывной двумерной сл. величины (X,Y) – вторая смешанная производная от F(x,y):
Свойства аналогичны свойствам одномерного случая
Слайд 144. Многомерные случайные величины. Условные законы распределения.
Условный закон распределения одной из
Условные плотности вероятности двумерной сл. величины (X, Y):
или
Числовые характеристики условных распределений: условные математические ожидания Мх(Y) и Му(Х) и условные дисперсии Dx(Y) и Dy(X) (находятся по обычным формулам математического ожидания и дисперсии, вместо вероятностей событий или плотностей вероятности используются условные вероятности или условные плотности вероятности).
Условное математическое ожидание случайной величины Y при Х=х, т. е. Мх(Y), есть функция от х, называемая функцией регрессии или просто регрессией Y по Х. График Мх(Y) - линия регрессии (кривая регрессии) Y по Х (аналогично для Мy(X))
Если случайные величины X и Y независимы, то
Слайд 154. Многомерные случайные величины. Условные законы распределения.
Зависимость между 2 сл. величинами
Ковариация Cov(X,Y) сл. величин X и Y - математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е.: где
Cov(X,Y) характеризует как степень зависимости сл. величин, так и их рассеяние вокруг точки (ax, ay).
Коэффициент корреляции 2 сл. величин - отношение их ковариации к произведению средних квадратических отклонений этих величин:
характеризует тесноту линейной зависимости
между случайными величинами
Свойства коэффициента корреляции:
Слайд 165. Двумерный (n-мерный) нормальный закон распределения.
Сл. величина (сл. вектор) (Х, Y)
,
числовые характеристики:
при этом одномерные сл. величины X и Y распределены нормально с параметрами соответственно
Условный закон распределения Y по Х - также нормальный с числовыми характеристиками (аналогично для My(X)):
т.е. линия регрессии Mx(Y) нормально распределенных случайных величин - прямая линия (нормальная регрессия Y по Х всегда линейна)
Понятие двумерного (n = 2) нормального закона обобщается для любого натурального n:
Слайд 176. Закон больших чисел и предельные теоремы.
1) Закон больших чисел (в
(т.е., при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности).
2) Теорема Чебышева. Если дисперсии n независимых сл. величин X1,X2,…,Xn ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая сл. величин сходится по вероятности к средней арифметической их математических ожиданий a1, a2,…,an, т. е.:
или
Слайд 186. Закон больших чисел и предельные теоремы.
3) Теорема Бернулли. Частость события
или
4) Согласно теореме Ляпунова, если независимые сл. величины Х1,Х2,…,Xn имеют конечные математические ожидания и дисперсии, по своему значению ни одна из этих сл. величин резко не выделяется среди остальных, то при закон распределения их суммы
неограниченно приближается к нормальному.
В частности, если Х1,Х2,…,Xn одинаково распределены, то закон распределения их суммы при неограниченно
приближается к нормальному.
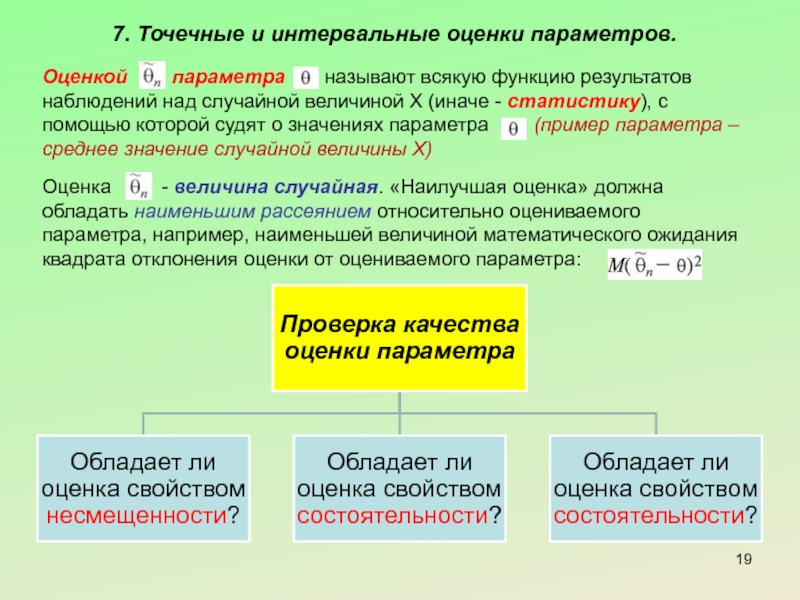
Слайд 197. Точечные и интервальные оценки параметров.
Оценкой параметра
Оценка - величина случайная. «Наилучшая оценка» должна обладать наименьшим рассеянием относительно оцениваемого параметра, например, наименьшей величиной математического ожидания квадрата отклонения оценки от оцениваемого параметра:
Слайд 207. Точечные и интервальные оценки параметров.
Оценка параметра
В противном случае оценка называется смещенной (присутствует систематическая ошибка).
Оценка параметра называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру: или
Несмещенная оценка параметра называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра, вычисленных по выборкам одного и того же объема n.
Для нахождения точечных и интервальных оценок параметров (характеристик) генеральной совокупности используется ряд основных методов:
метод моментов;
метод максимального правдоподобия.
Слайд 217. Точечные и интервальные оценки параметров.
Пример точечных оценок параметров распределения сл.
- выборочная средняя - несмещенная, состоятельная
и эффективная (для нормально распределенной генеральной
совокупности) оценка математического ожидания а сл. в. X
- выборочная дисперсия - смещенная, но
состоятельная оценка дисперсии
- исправленная выборочная дисперсия –
несмещенная и состоятельная оценка дисперсии
Интервальной оценкой параметра называется числовой интервал
который с заданной вероятностью накрывает неизвестное значение параметра
Интервал называется доверительным, а вероятность - доверительной вероятностью или надежностью оценки
Пример интервальных оценок: доверительные интервалы для генеральной средней, для генеральной дисперсии на уровне значимости
Слайд 228. Проверка (тестирование) статистических гипотез
Последовательность тестирования статистической гипотезы:
используется специально составленная выборочная
по этому выборочному распределению определяется критическое значение такое, что если гипотеза Н0 верна, то вероятность мала; так что в условиях данного исследования событие можно считать практически невозможным;
если обнаруживается отклонение , то гипотеза Н0 отвергается, появление значения считается совместимым с гипотезой Н0, которая принимается (не отвергается).
Правило, по которому гипотеза Н0 отвергается или принимается, называется статистическим критерием или статистическим тестом.
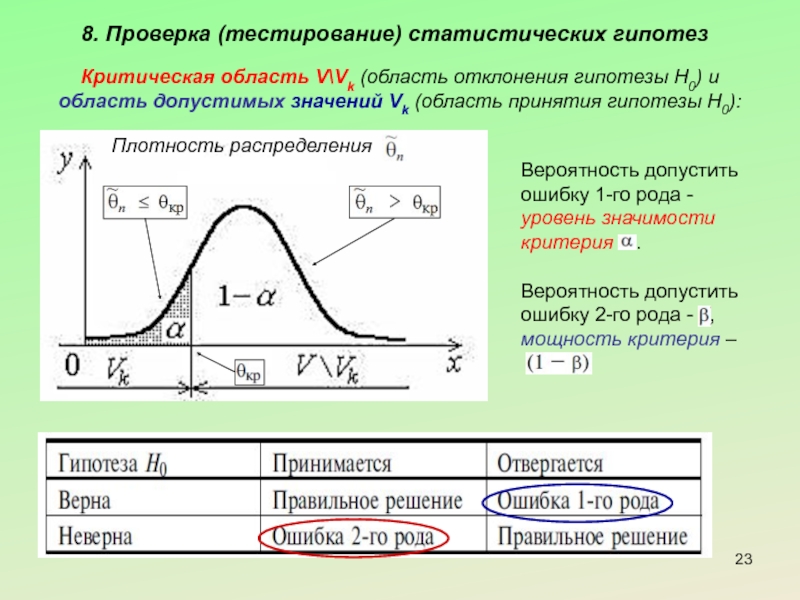
Слайд 238. Проверка (тестирование) статистических гипотез
Критическая область V\Vk (область отклонения гипотезы H0)
область допустимых значений Vk (область принятия гипотезы H0):
Плотность распределения
Вероятность допустить ошибку 1-го рода - уровень значимости
критерия .
Вероятность допустить ошибку 2-го рода - ,
мощность критерия –
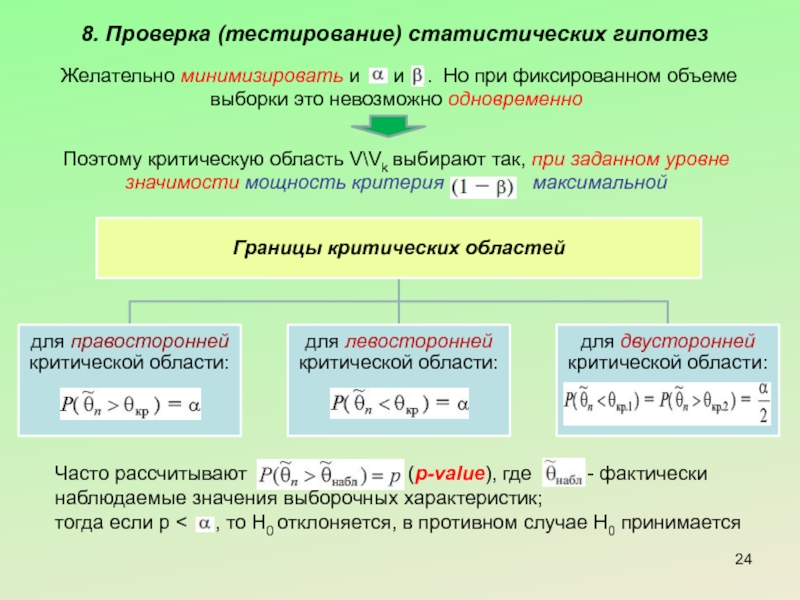
Слайд 248. Проверка (тестирование) статистических гипотез
Поэтому критическую область V\Vk выбирают так, при
Желательно минимизировать и и . Но при фиксированном объеме выборки это невозможно одновременно
Часто рассчитывают (p-value), где - фактически наблюдаемые значения выборочных характеристик;
тогда если p < , то H0 отклоняется, в противном случае H0 принимается
Слайд 25Вопросы изученные в Теме 1:
32
Случайные величины и их числовые характеристики.
Функция распределения
Некоторые распределения случайных величин.
Многомерные случайные величины. Условные законы распределения.
Двумерный (n-мерный) нормальный закон распределения.
Закон больших чисел и предельные теоремы.
Точечные и интервальные оценки параметров.
Проверка (тестирование) статистических гипотез