- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Развертки поверхностей. (Лекция 7а) презентация
Содержание
- 1. Развертки поверхностей. (Лекция 7а)
- 2. Основные положения Развертыванием называется такое преобразование, при
- 3. Развертки прямых круговых конуса и цилиндра
- 4. Способ нормального сечения Определяются натуральные величины образующих,
- 5. a2 b2 c2 А2 Боковые ребра
- 6. А2 На П2 проводим след
- 7. P2 12 22 32 А2
- 8. c1 b1 a1 P2 12
- 9. c1 b1 a1 P2 12 22
- 10. c1 b1 a1 P2 12 22
Основные положения Развертыванием называется такое преобразование, при котором все точки поверхности совмещаются с плоскостью. Развертка - плоская фигура, получаемая в результате данного преобразования. Поверхности делятся на развертываемые и неразвертываемые. Развертываемые совмещаются
Слайд 2Основные положения
Развертыванием называется такое преобразование, при котором все точки поверхности совмещаются
с плоскостью.
Развертка - плоская фигура, получаемая в результате данного преобразования.
Поверхности делятся на развертываемые и неразвертываемые.
Развертываемые совмещаются с плоскостью без разрывов и складок
Для неразвертываемых строятся условные развертки
Развертка - плоская фигура, получаемая в результате данного преобразования.
Поверхности делятся на развертываемые и неразвертываемые.
Развертываемые совмещаются с плоскостью без разрывов и складок
Для неразвертываемых строятся условные развертки
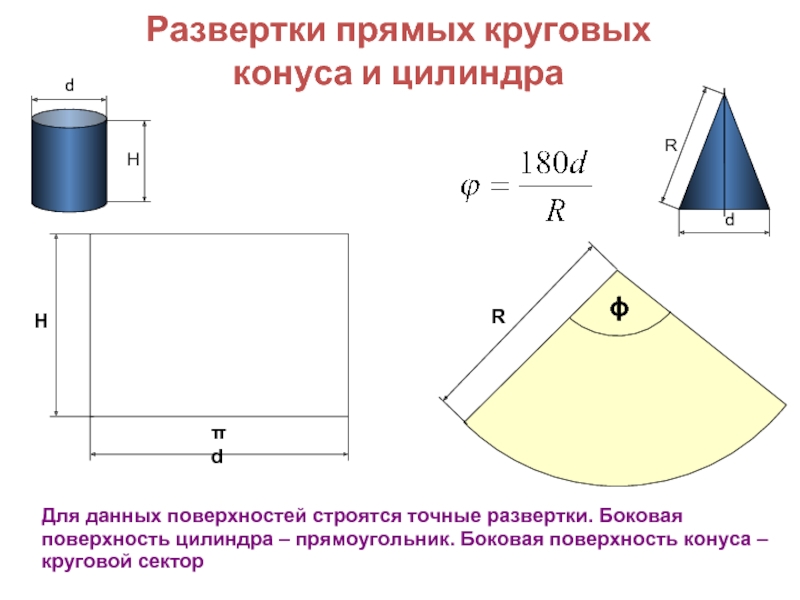
Слайд 3Развертки прямых круговых
конуса и цилиндра
Н
πd
Н
d
Для данных поверхностей строятся точные развертки. Боковая
поверхность цилиндра – прямоугольник. Боковая поверхность конуса – круговой сектор
ϕ
Слайд 4Способ нормального сечения
Определяются натуральные величины образующих, если они заданы в общем
положении.
Строится нормальное сечение (там, где образующие имеют истинную величину)
Определяется натуральная величина нормального сечения
Строится развертка: периметр нормального сечение «развертывается» в прямую; через его вершины перпендикулярно линии проводятся образующие
Строится нормальное сечение (там, где образующие имеют истинную величину)
Определяется натуральная величина нормального сечения
Строится развертка: периметр нормального сечение «развертывается» в прямую; через его вершины перпендикулярно линии проводятся образующие
Применяется для призматических и цилиндрических поверхностей. Нормальное сечение перпендикулярно образующим и определяет расстояние между ними
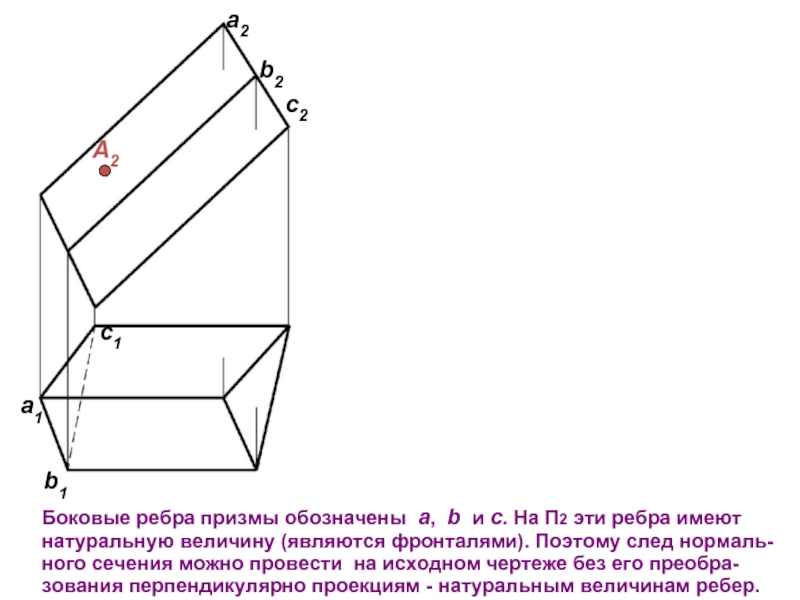
Слайд 5a2
b2
c2
А2
Боковые ребра призмы обозначены a, b и c. На П2 эти
ребра имеют натуральную величину (являются фронталями). Поэтому след нормаль-ного сечения можно провести на исходном чертеже без его преобра-зования перпендикулярно проекциям - натуральным величинам ребер.
c1
b1
a1
Слайд 6
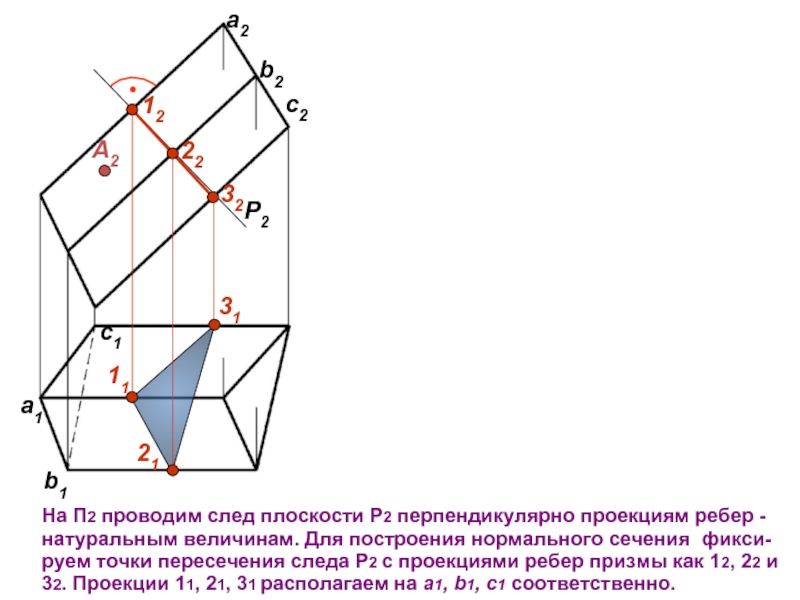
А2
На П2 проводим след плоскости Р2 перпендикулярно проекциям ребер - натуральным
величинам. Для построения нормального сечения фикси- руем точки пересечения следа Р2 с проекциями ребер призмы как 12, 22 и 32. Проекции 11, 21, 31 располагаем на a1, b1, c1 соответственно.
b1
a1
c1
Слайд 7
P2
12
22
32
А2
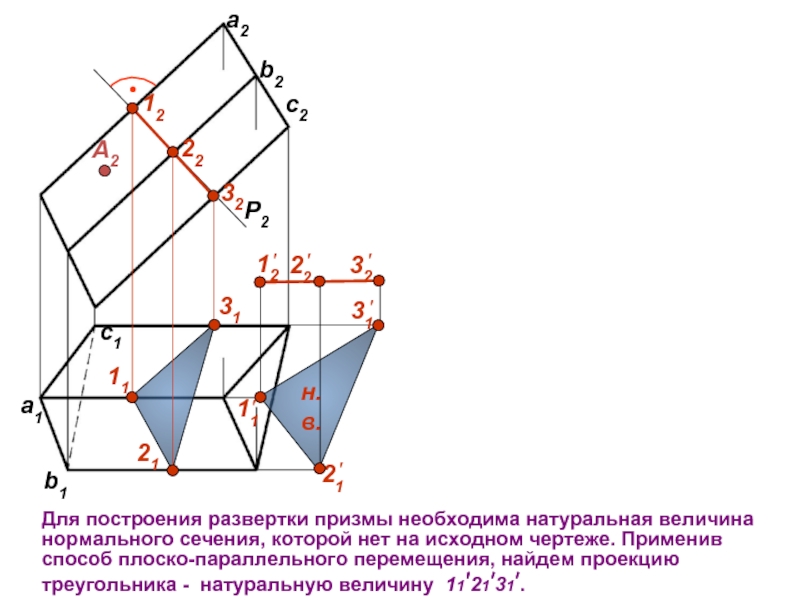
Для построения развертки призмы необходима натуральная величина нормального сечения, которой нет
на исходном чертеже. Применив способ плоско-параллельного перемещения, найдем проекцию треугольника - натуральную величину 11′21′31′.
c1
b1
a1
Слайд 8c1
b1
a1
P2
12
22
32
11
31
21
А2
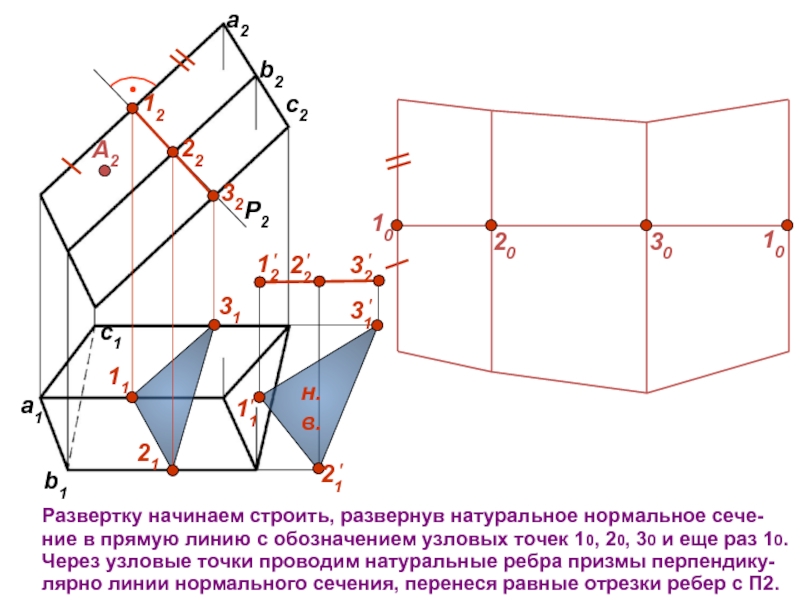
Развертку начинаем строить, развернув натуральное нормальное сече- ние в прямую линию
с обозначением узловых точек 10, 20, 30 и еще раз 10. Через узловые точки проводим натуральные ребра призмы перпендику- лярно линии нормального сечения, перенеся равные отрезки ребер с П2.
н.в.
Слайд 9c1
b1
a1
P2
12
22
32
11
31
21
А2
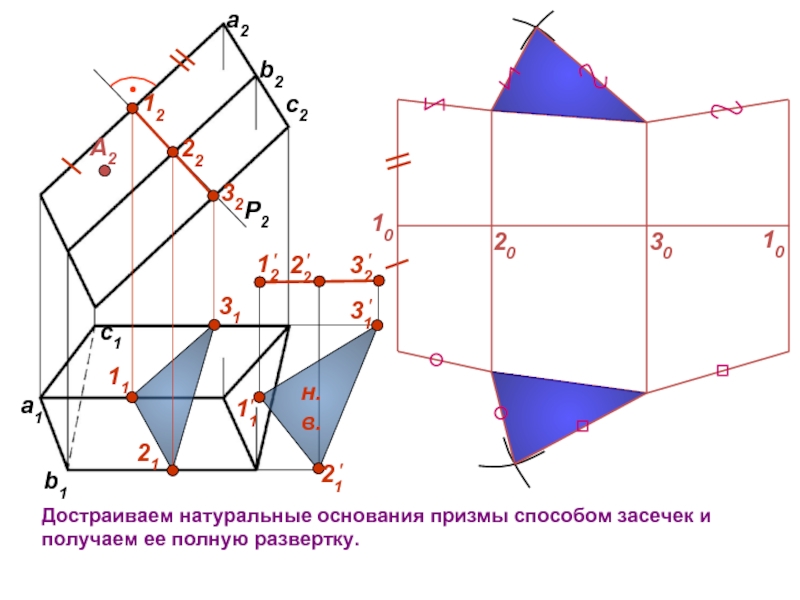
Достраиваем натуральные основания призмы способом засечек и получаем ее полную развертку.
н.в.
Слайд 10c1
b1
a1
P2
12
22
32
11
31
21
А2
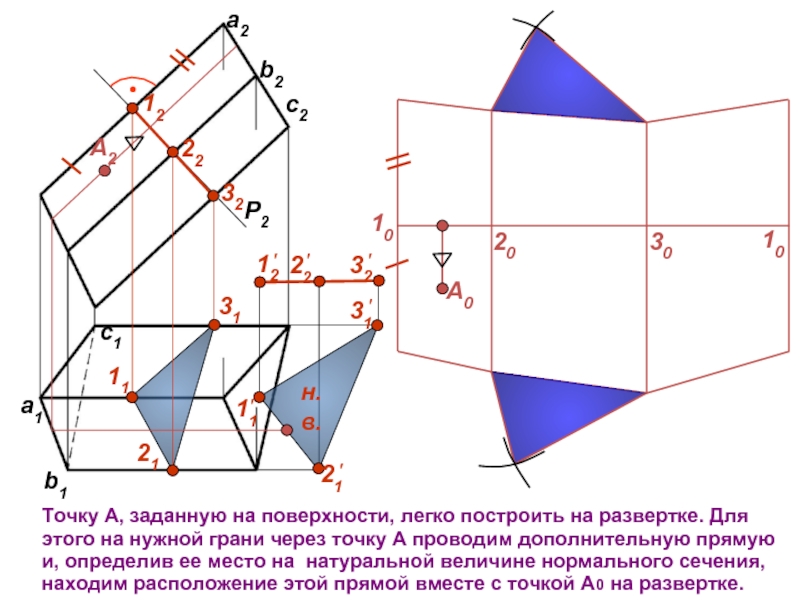
Точку А, заданную на поверхности, легко построить на развертке. Для этого
на нужной грани через точку А проводим дополнительную прямую и, определив ее место на натуральной величине нормального сечения, находим расположение этой прямой вместе с точкой А0 на развертке.
н.в.
