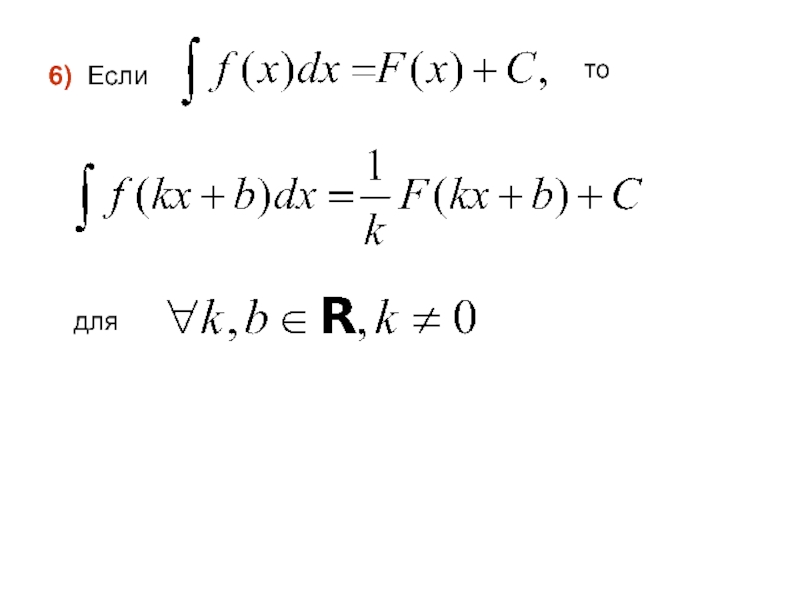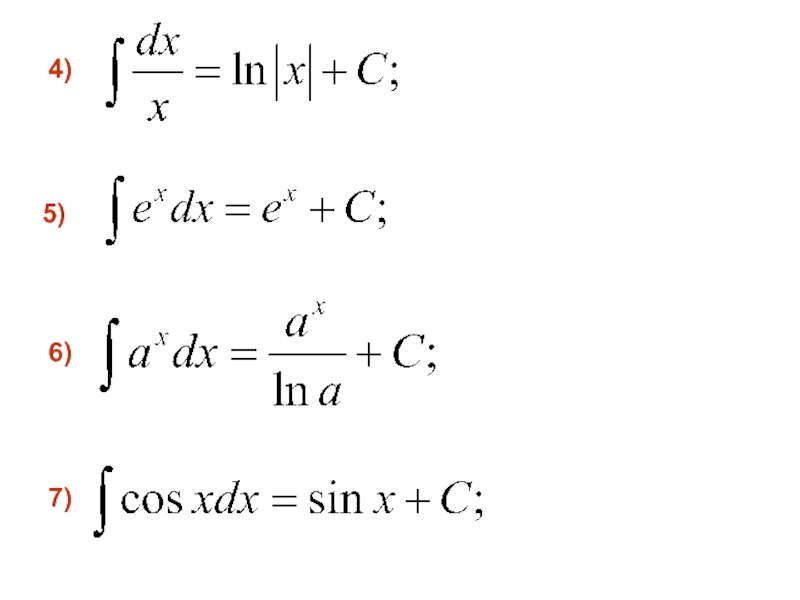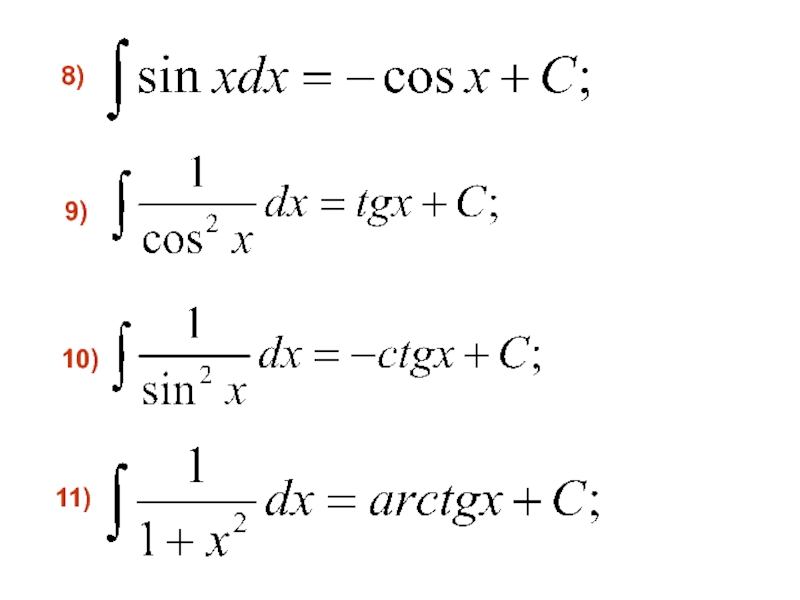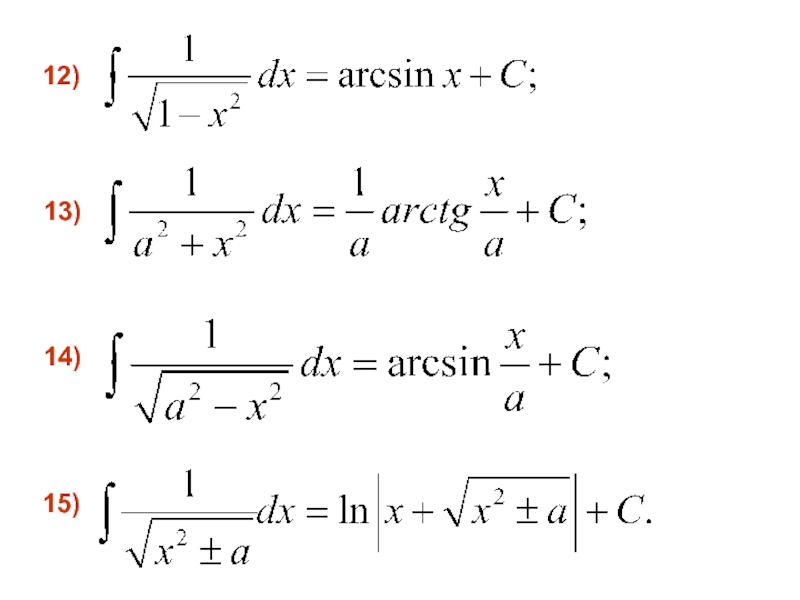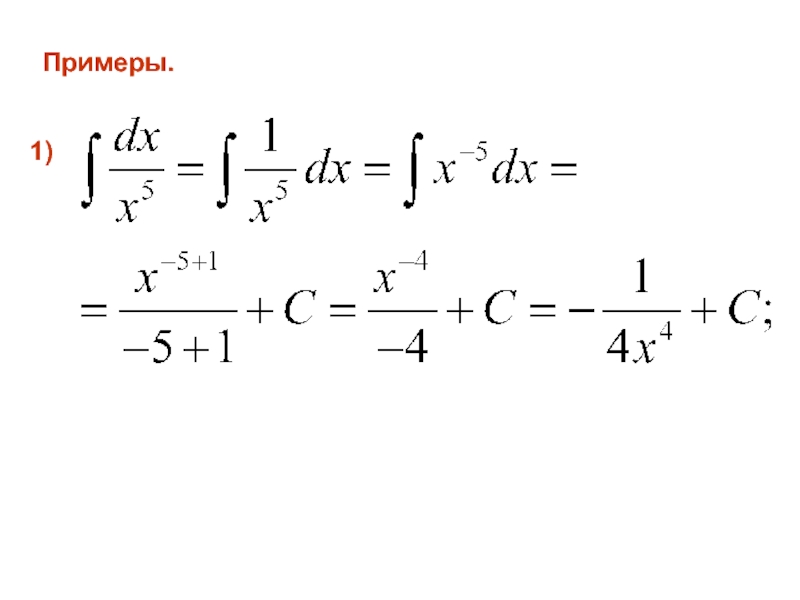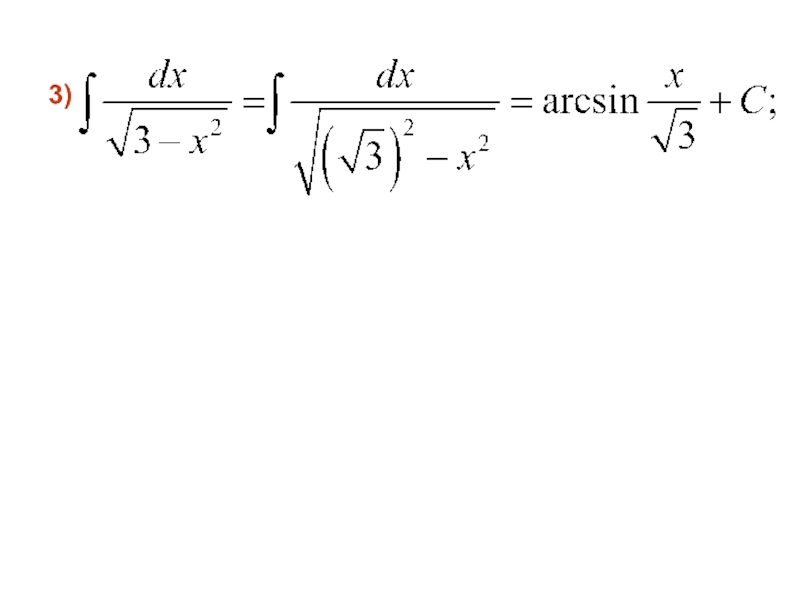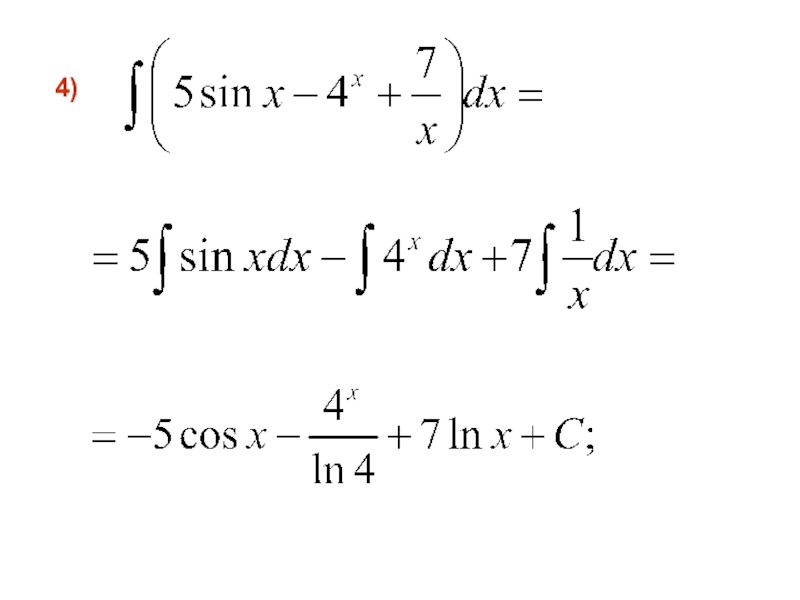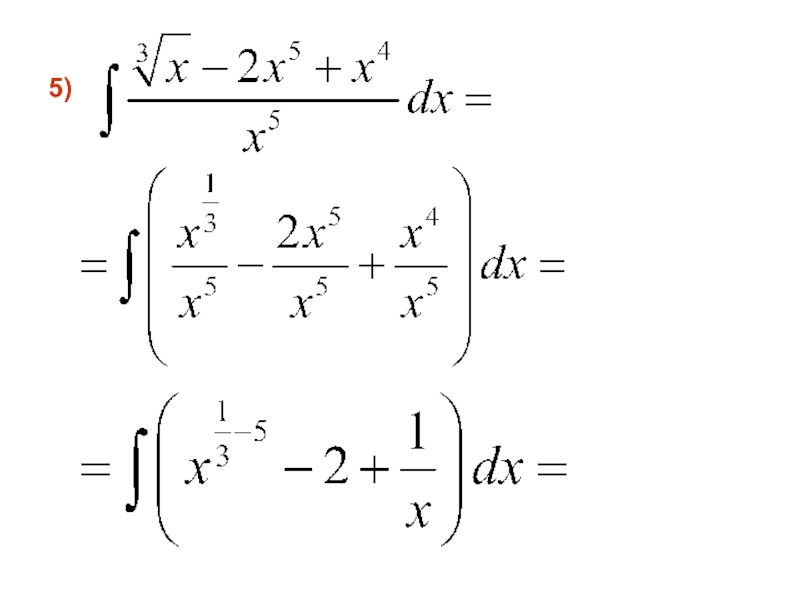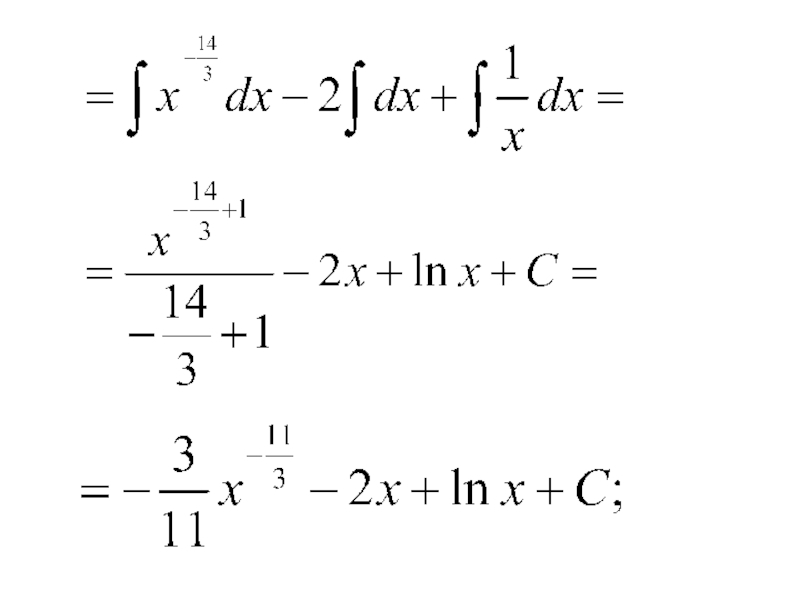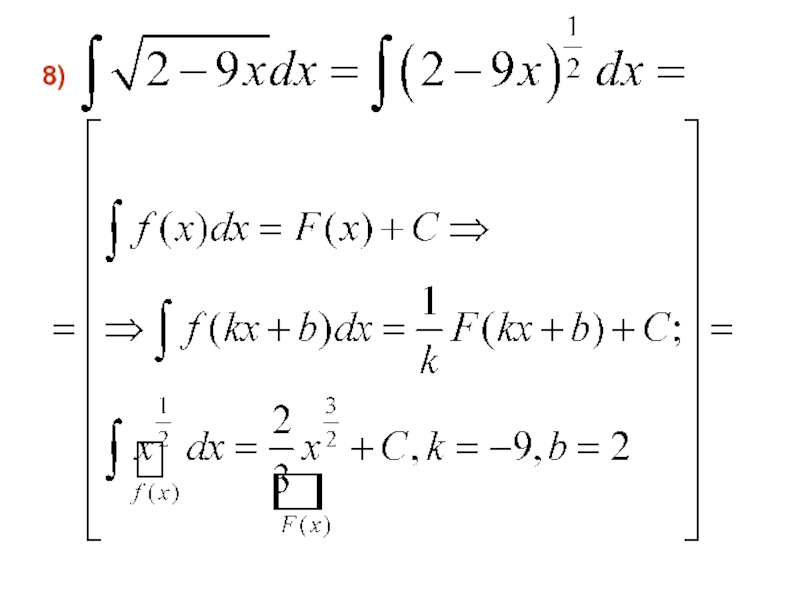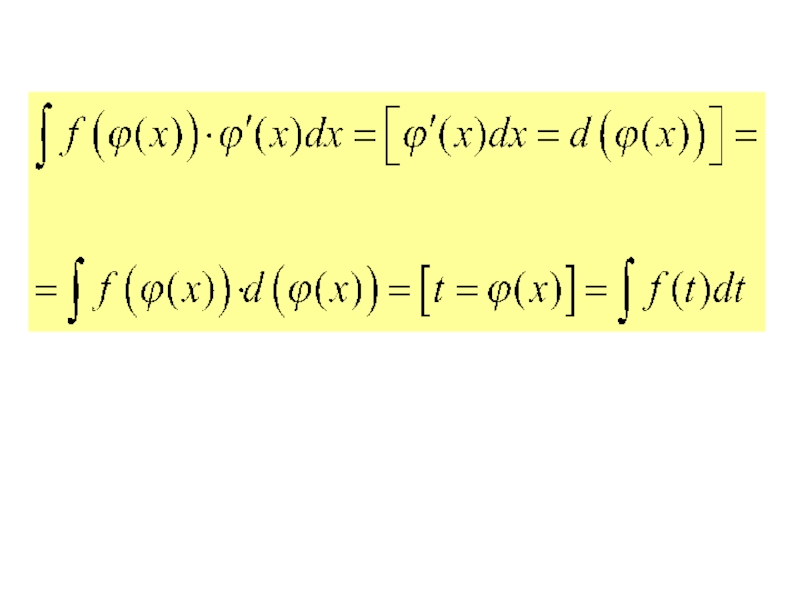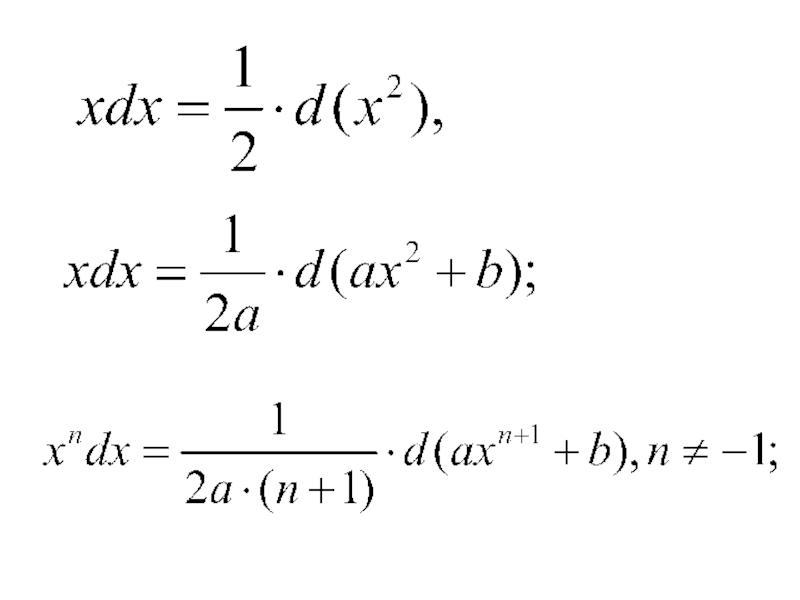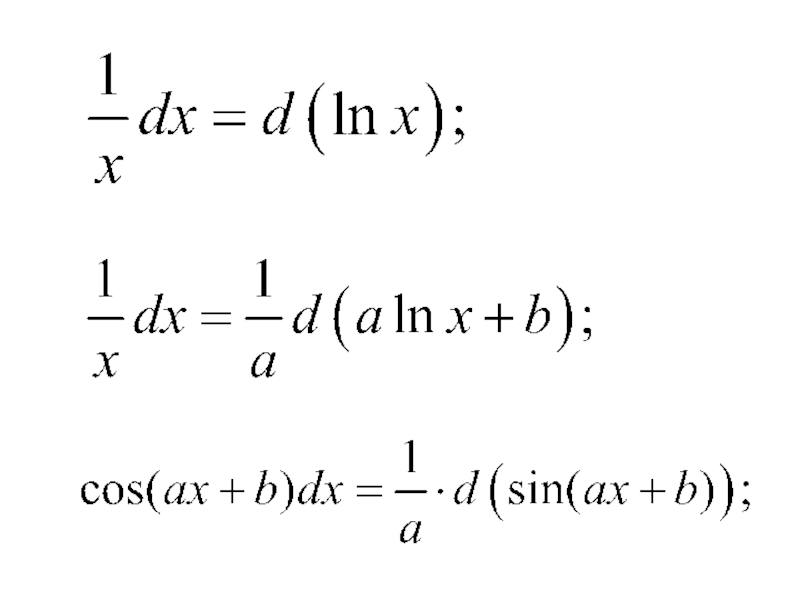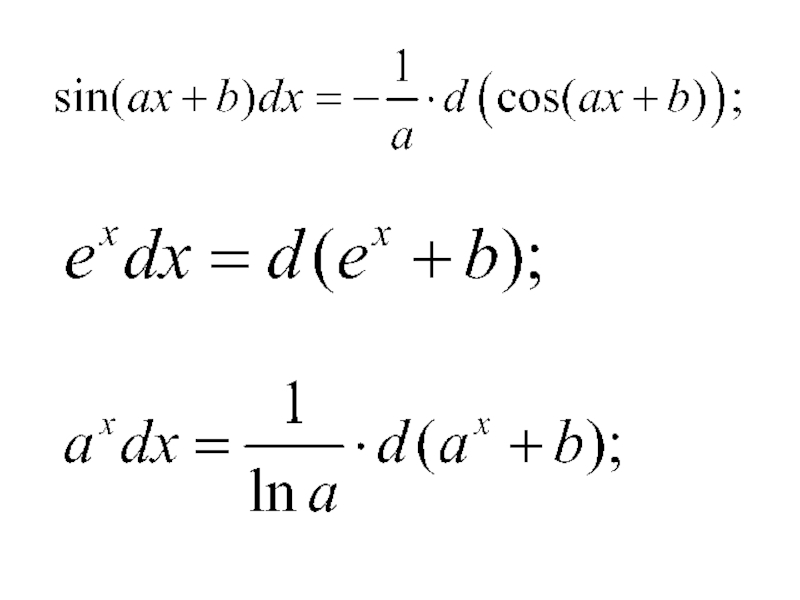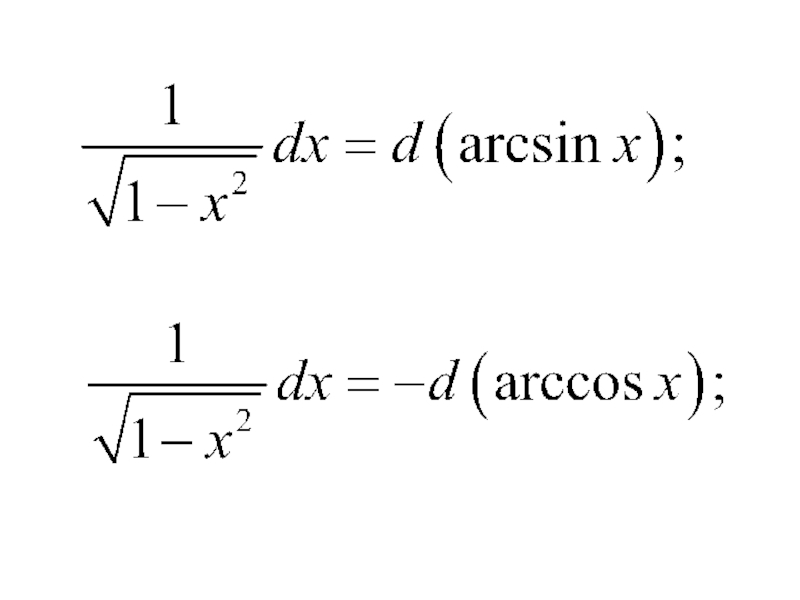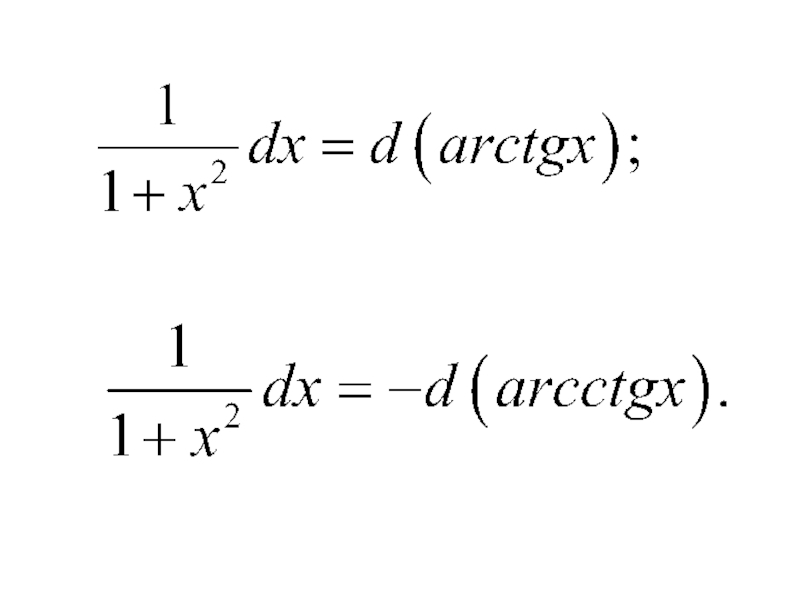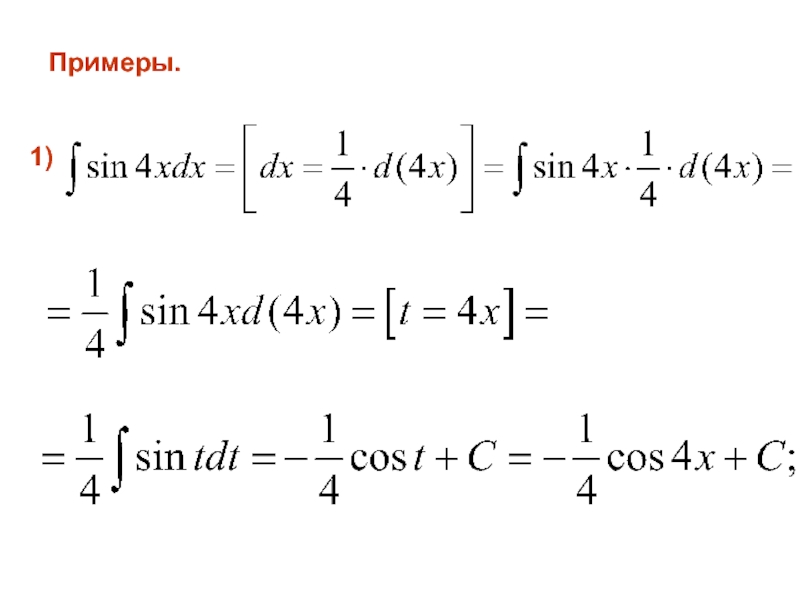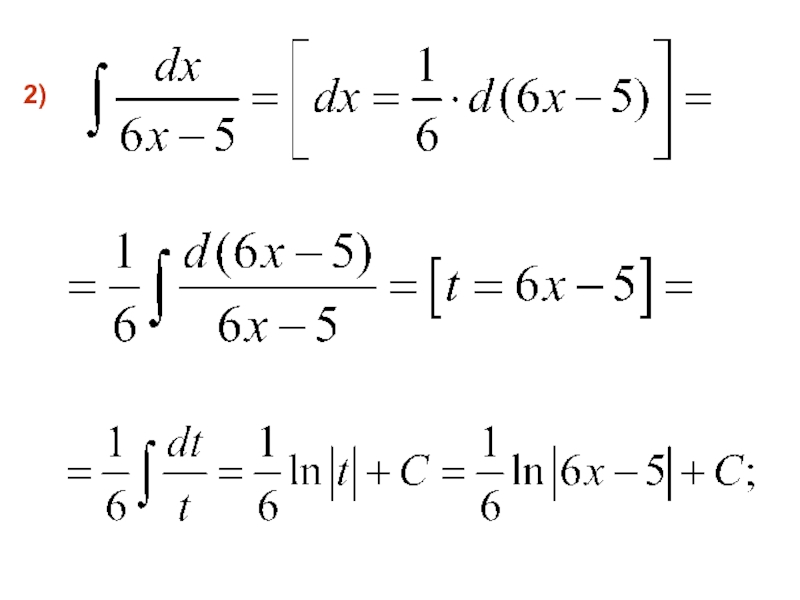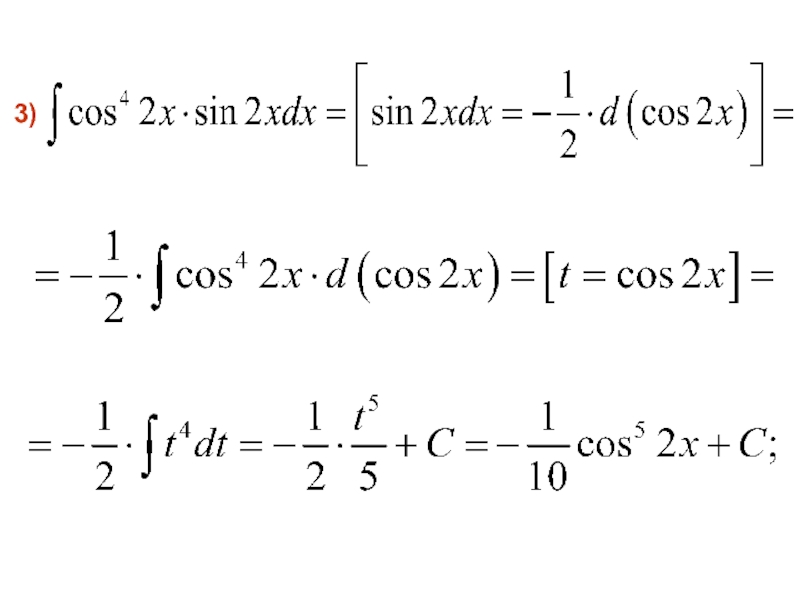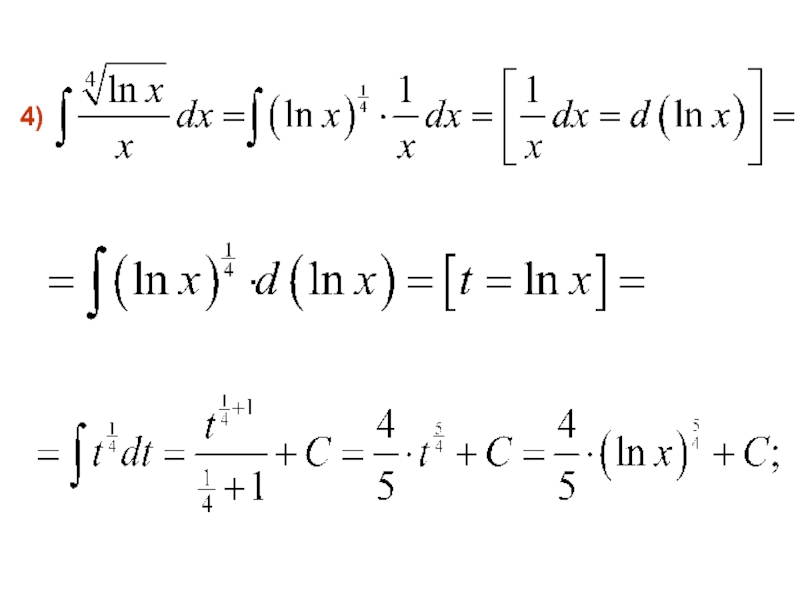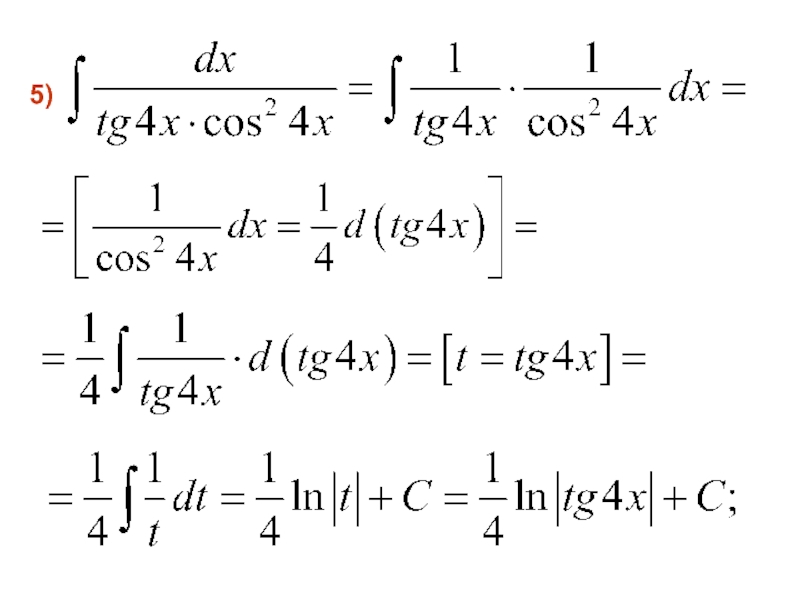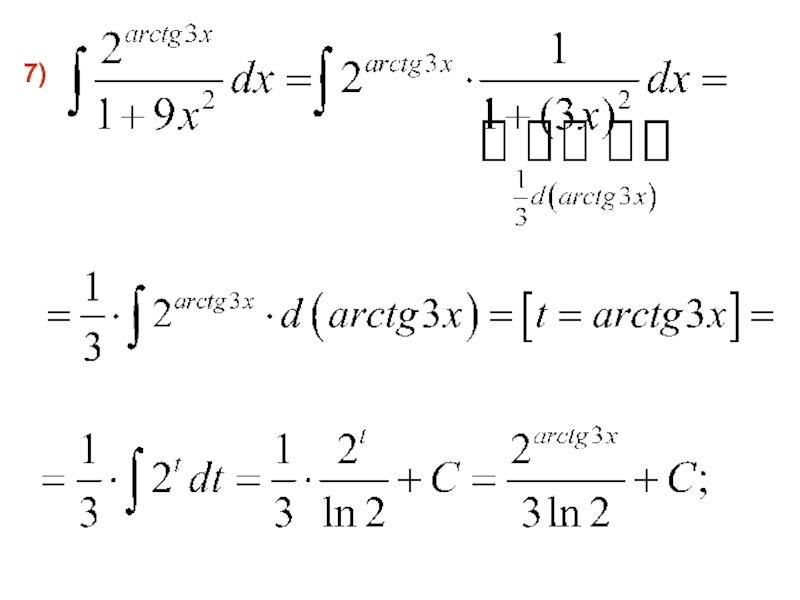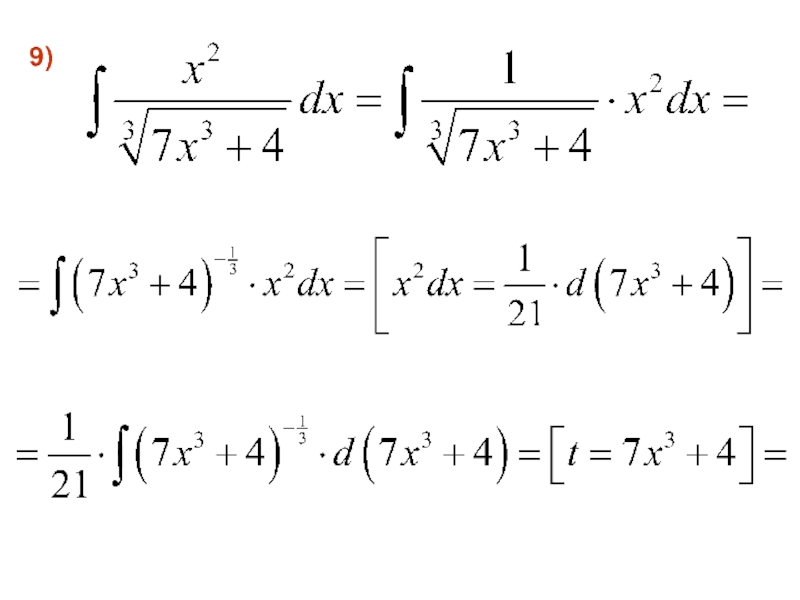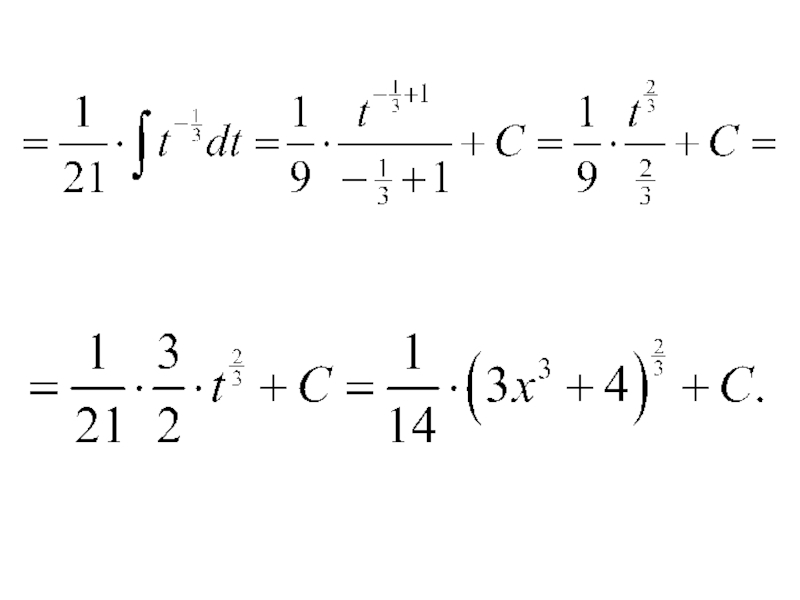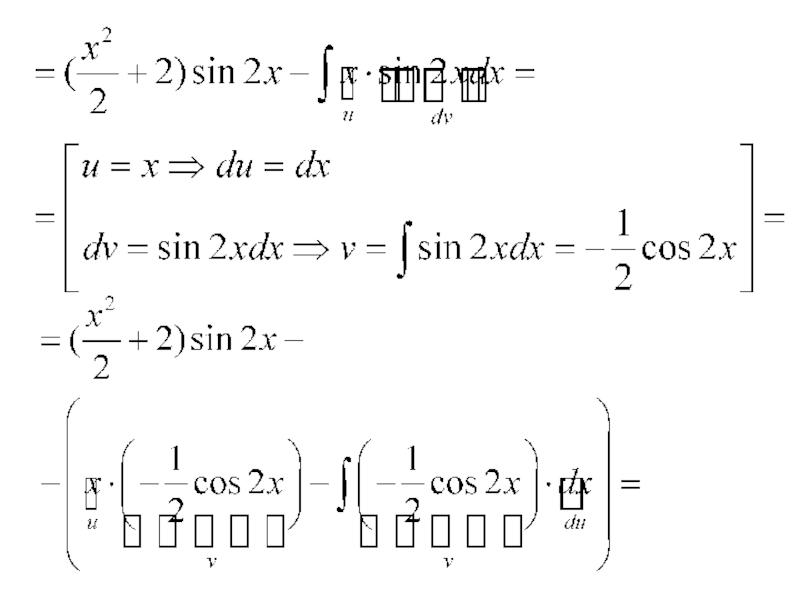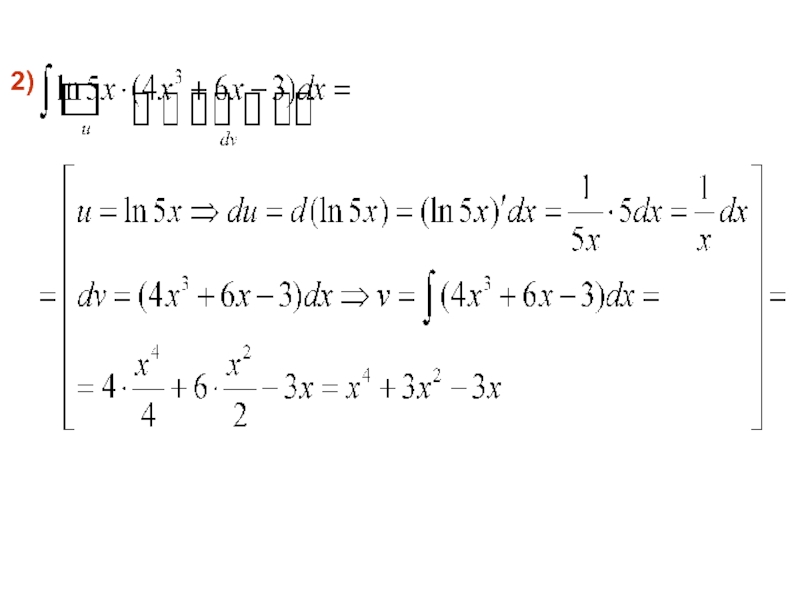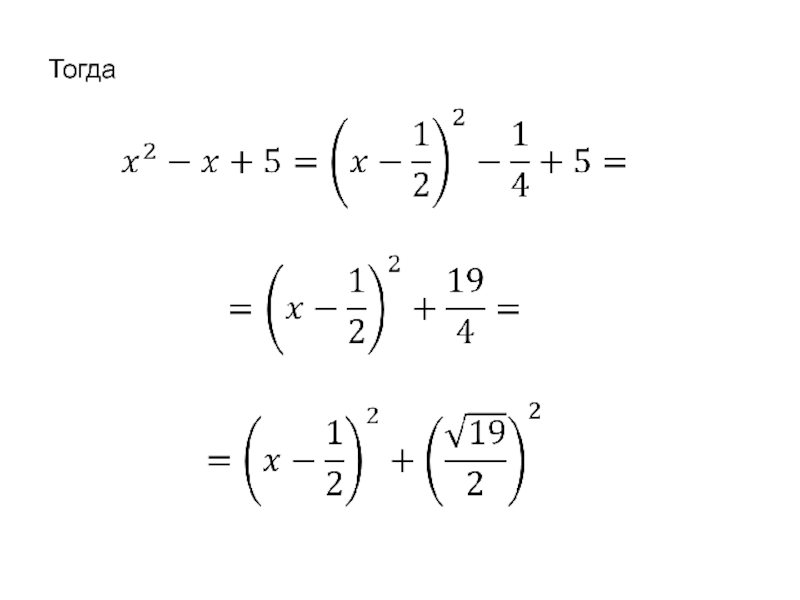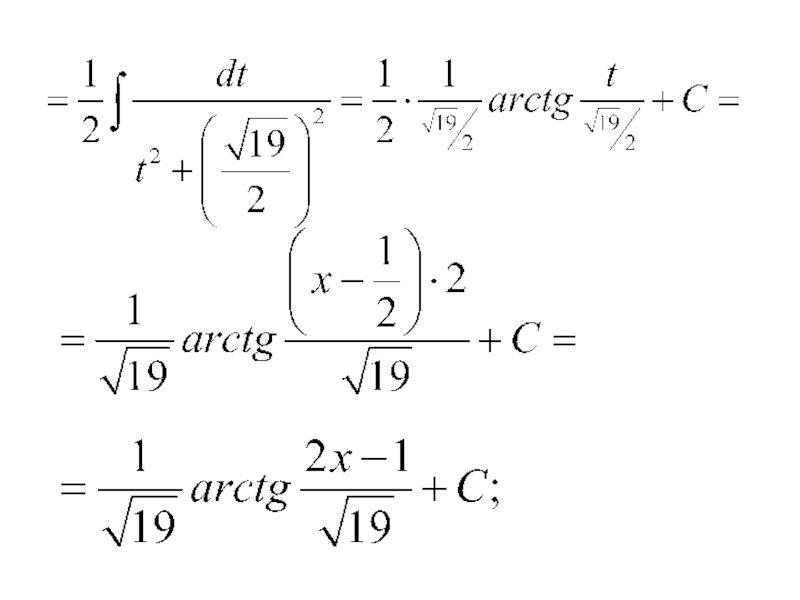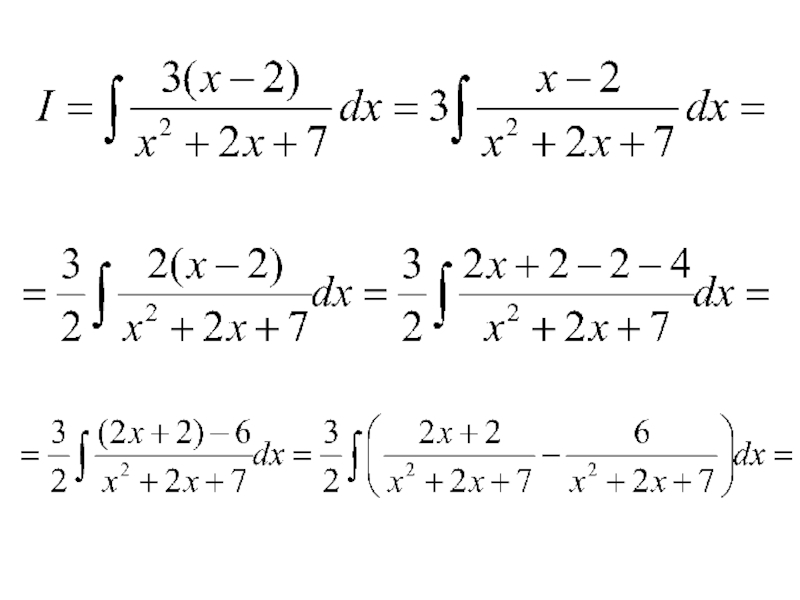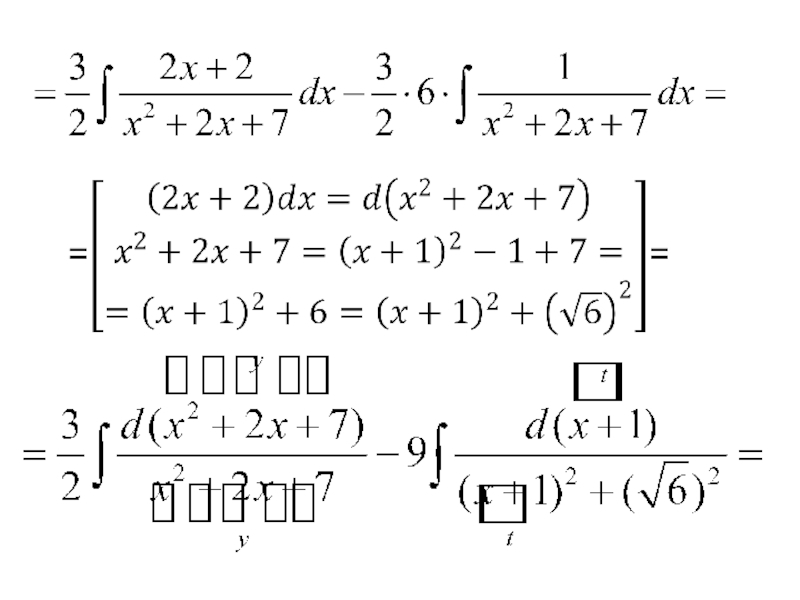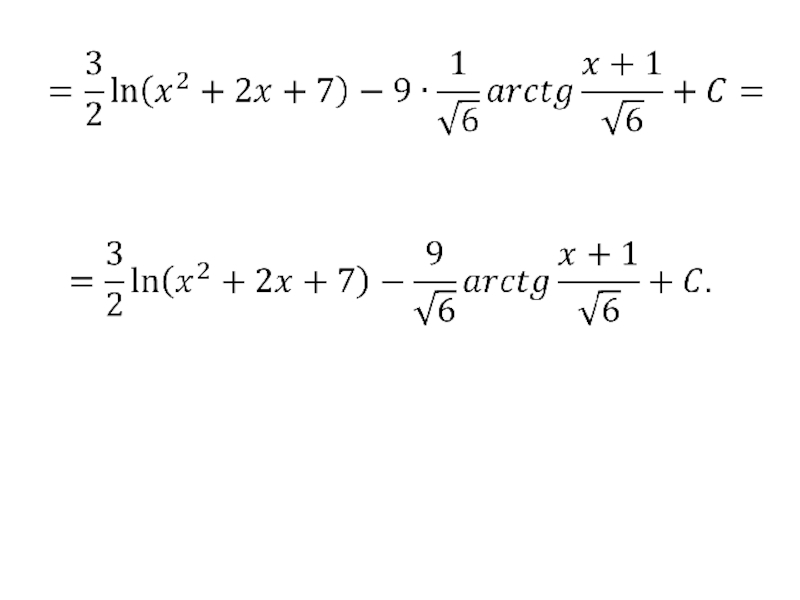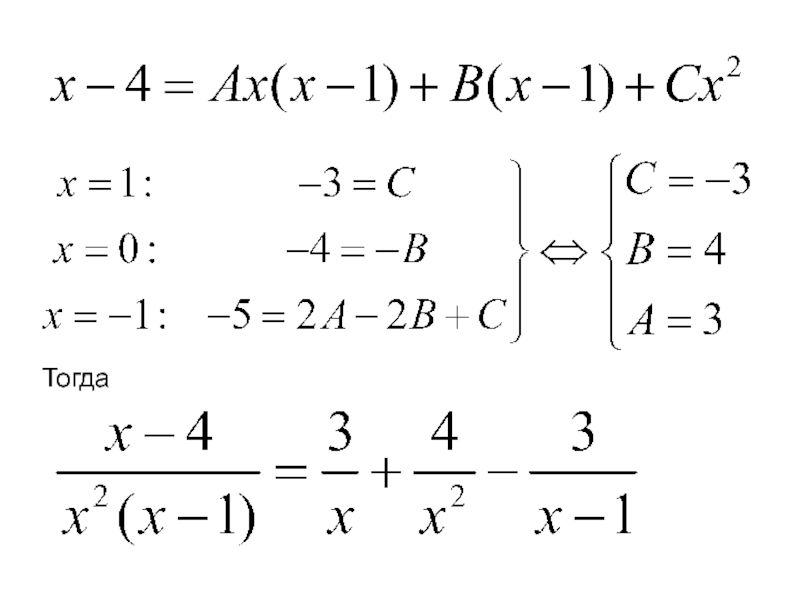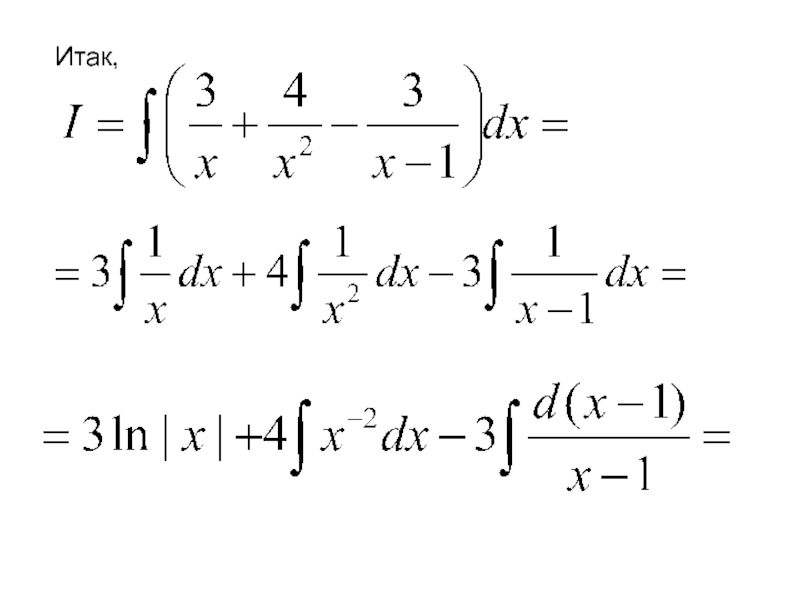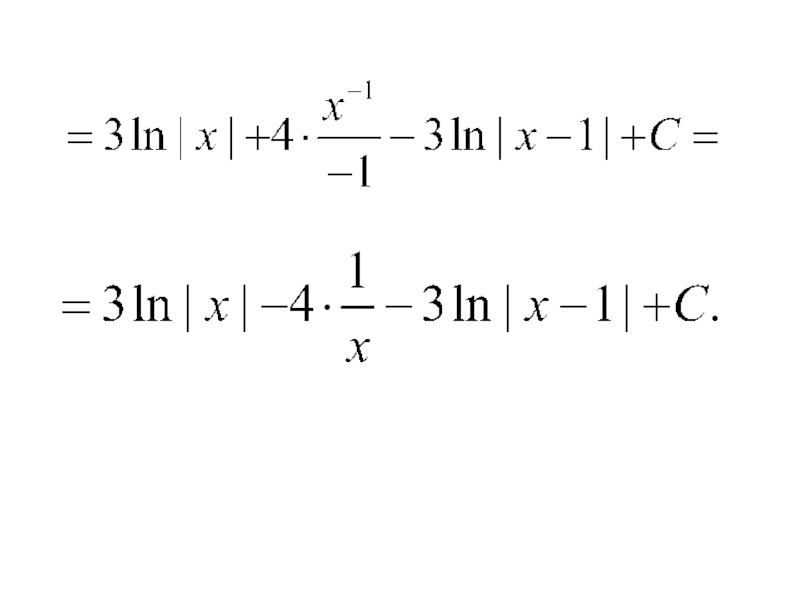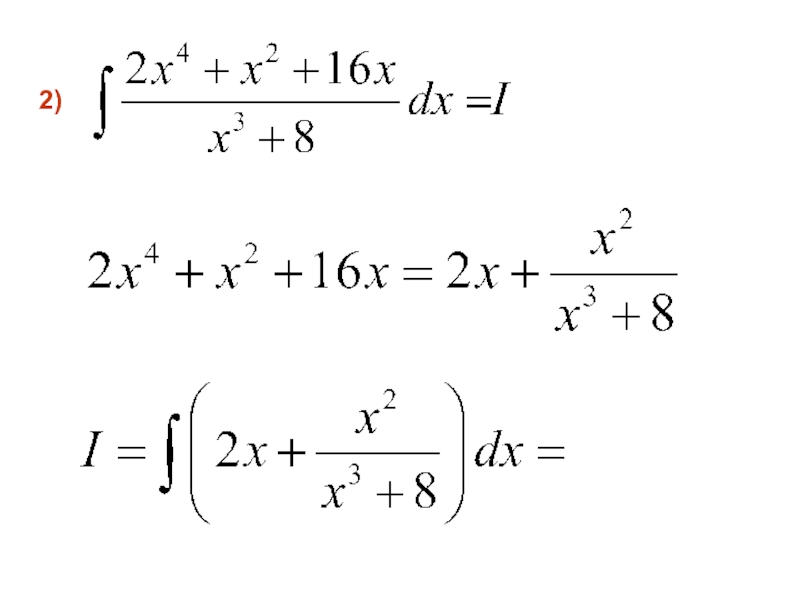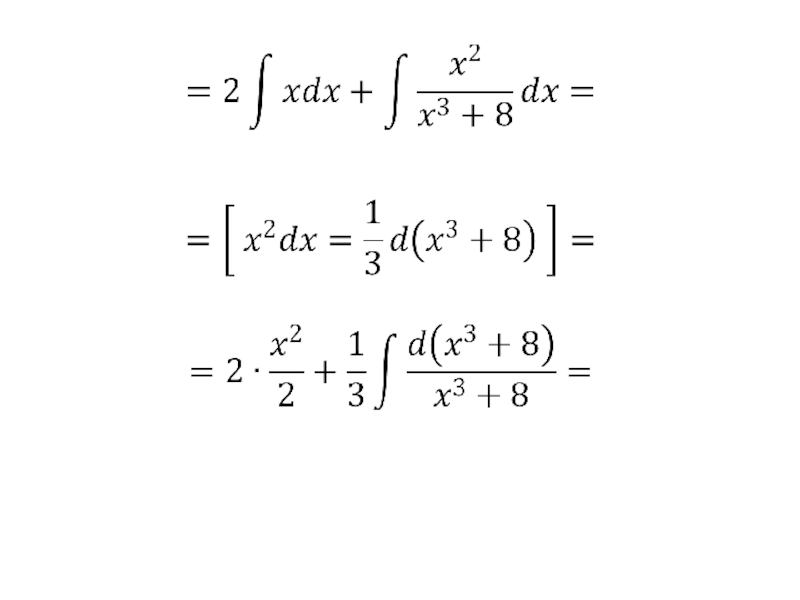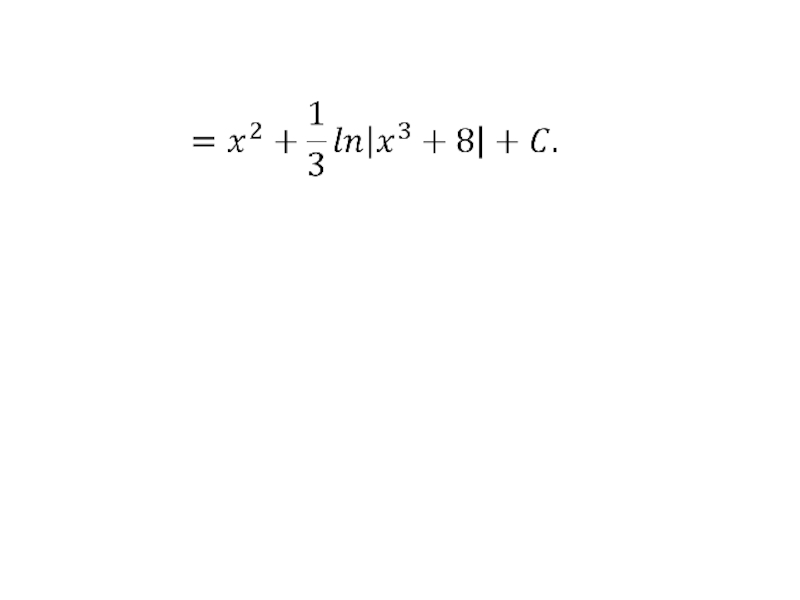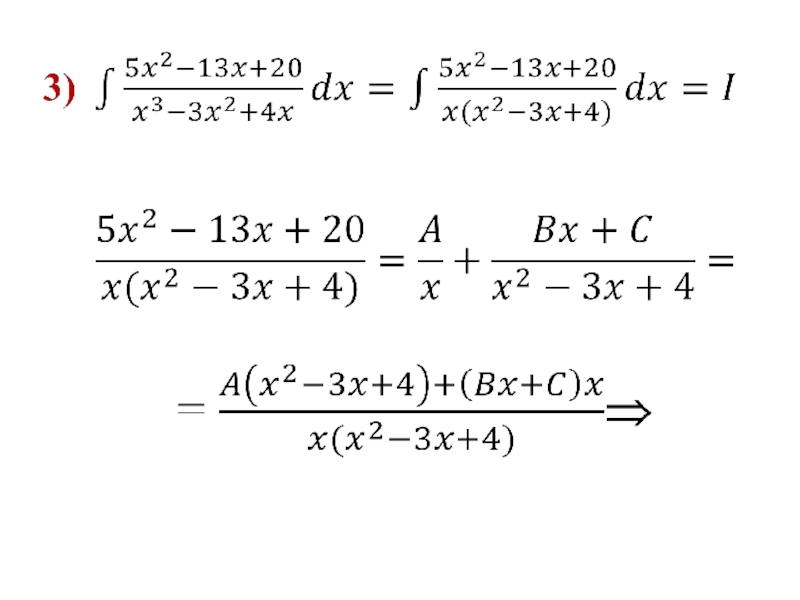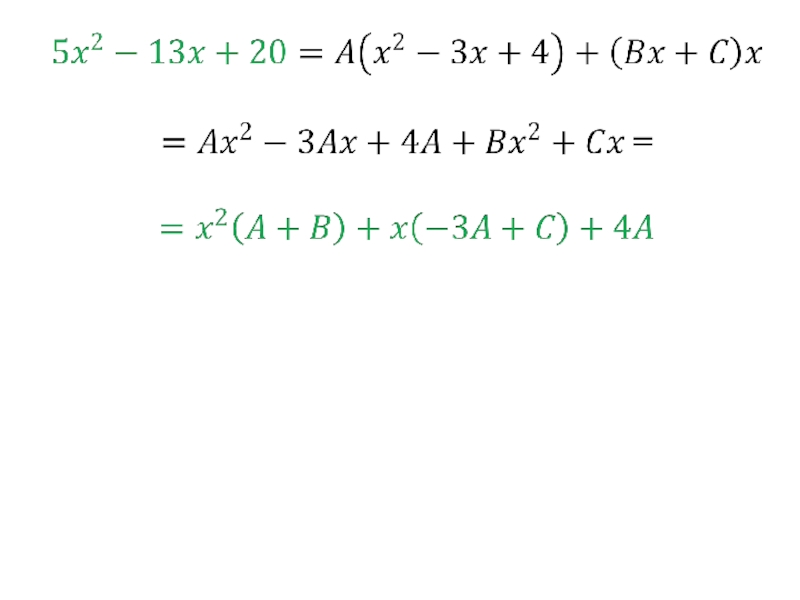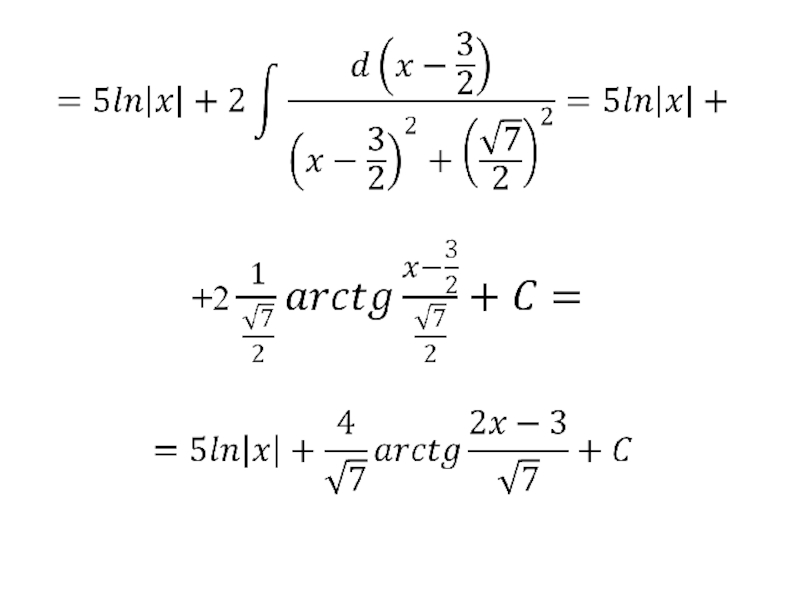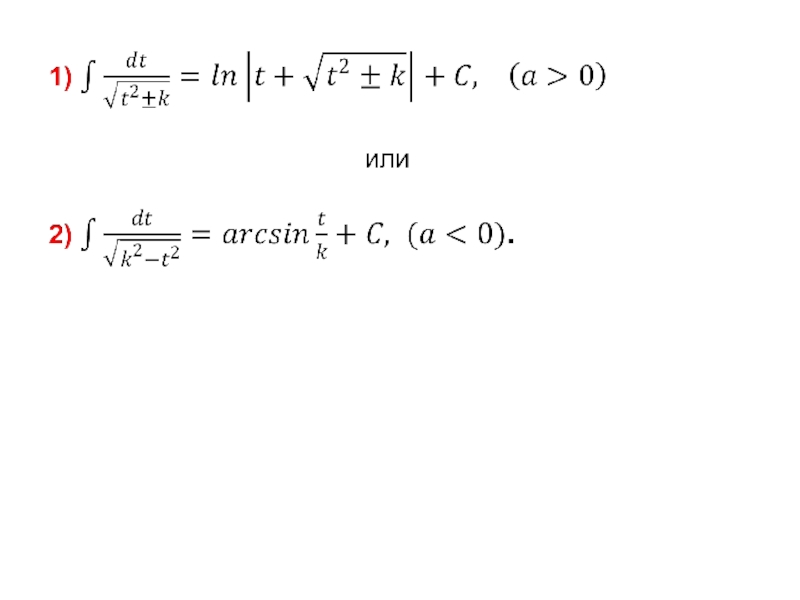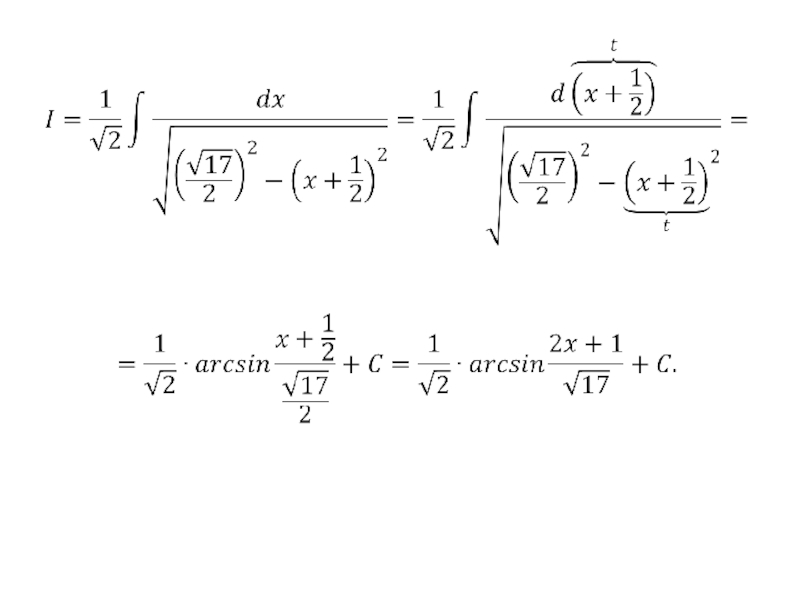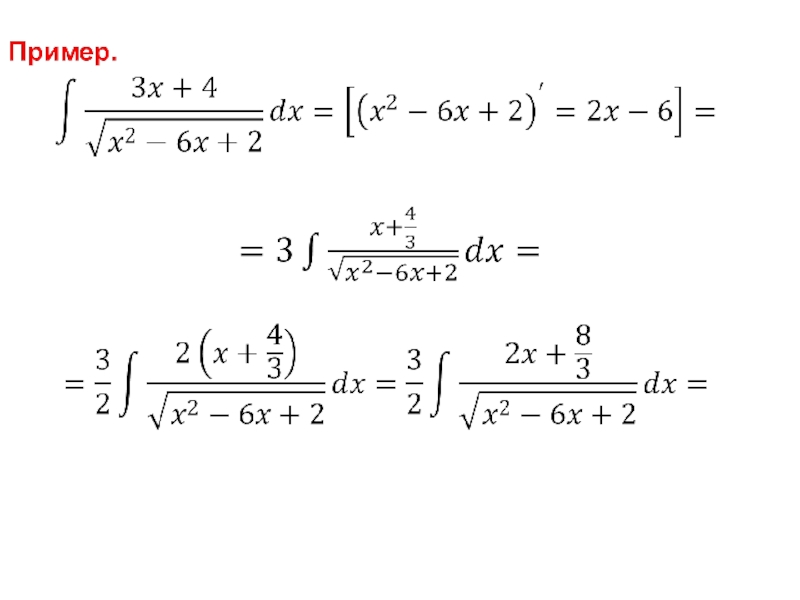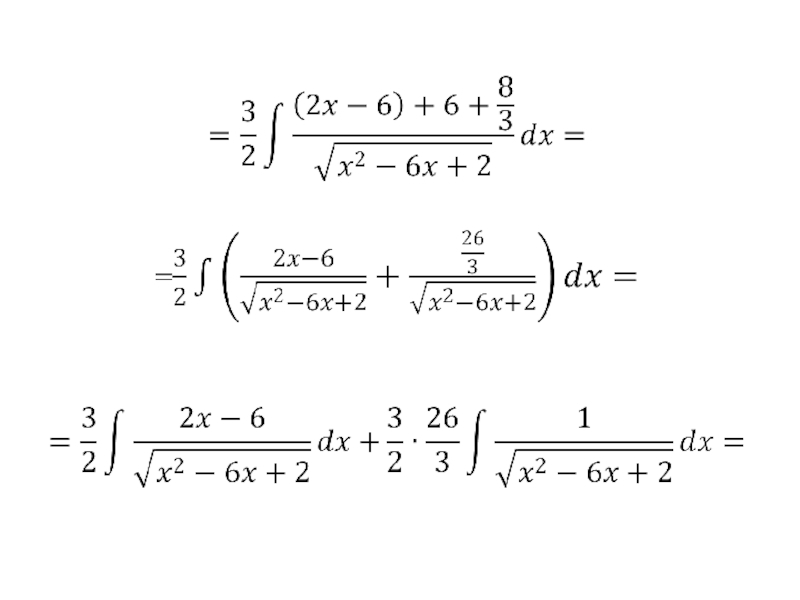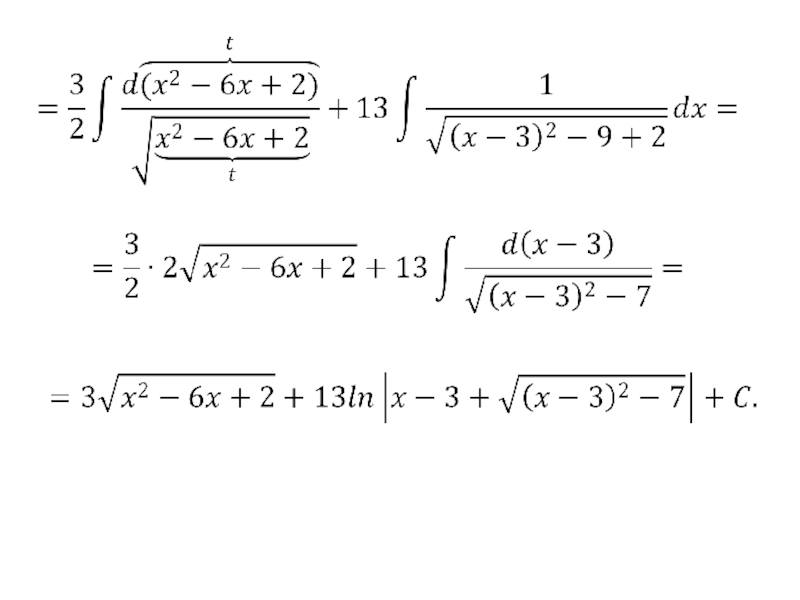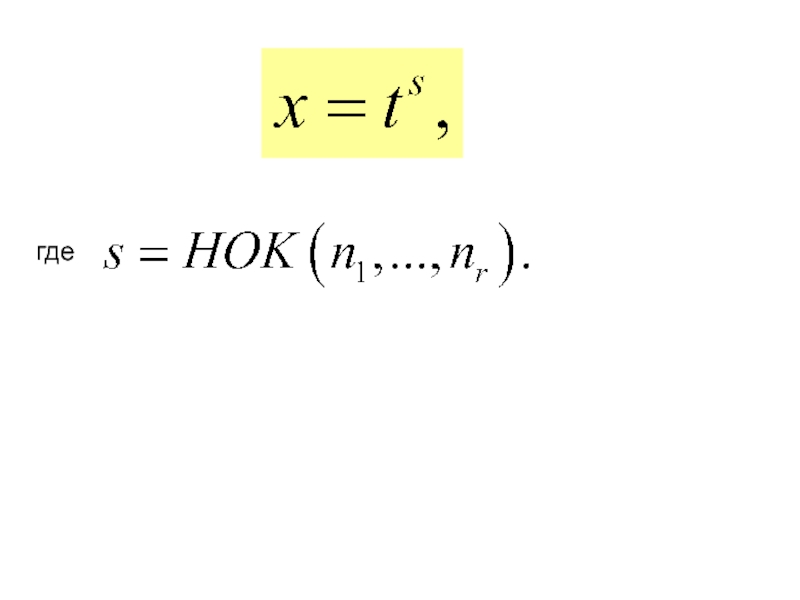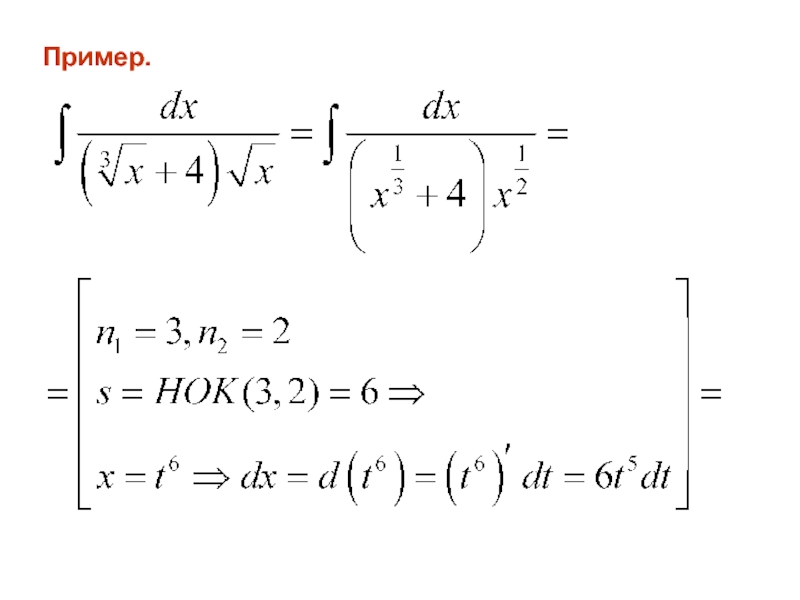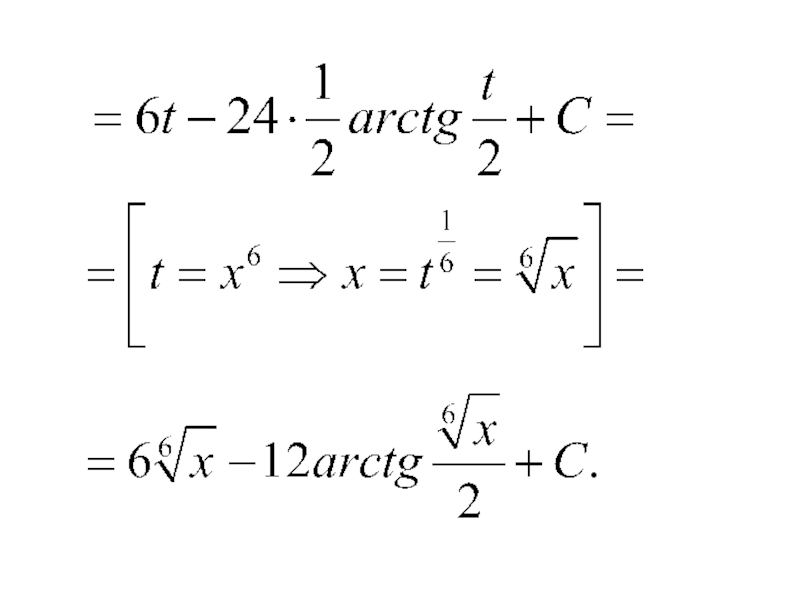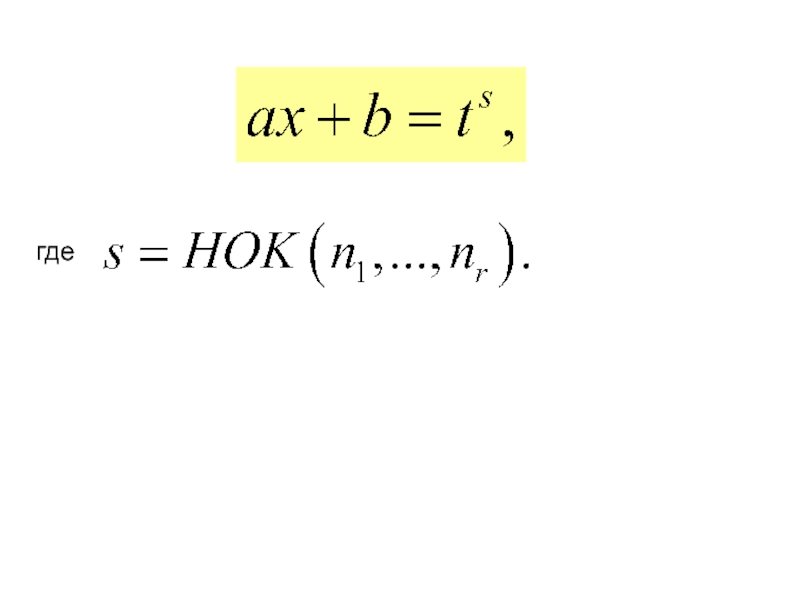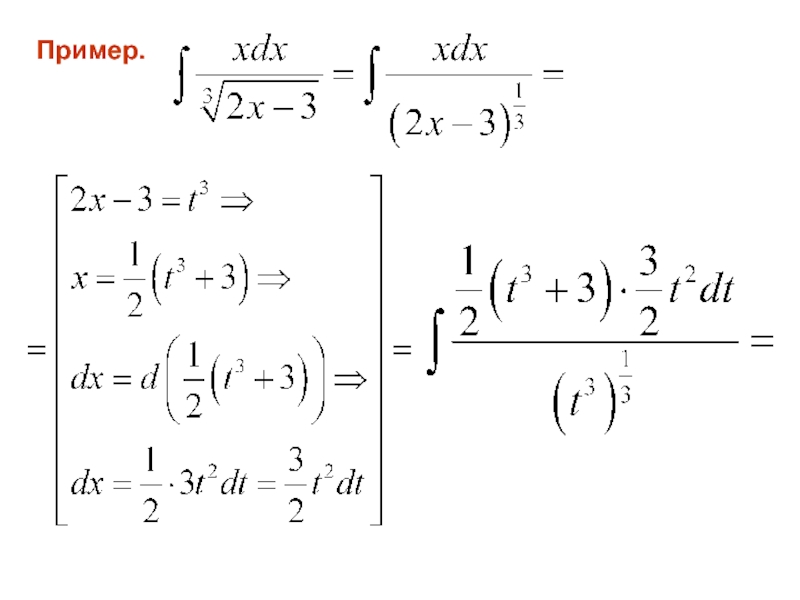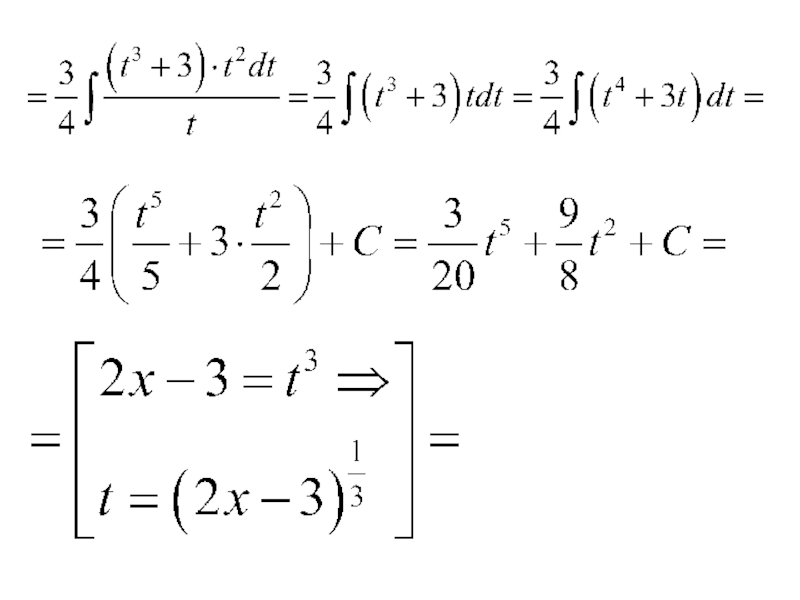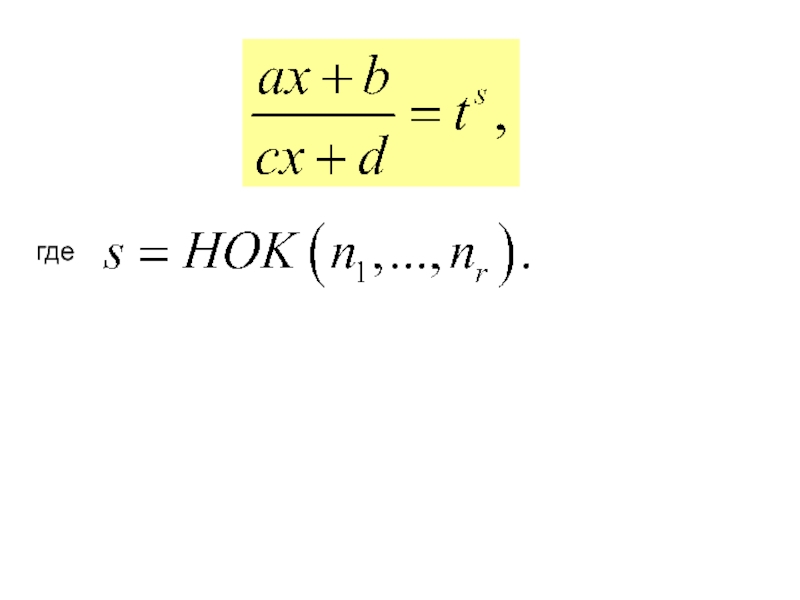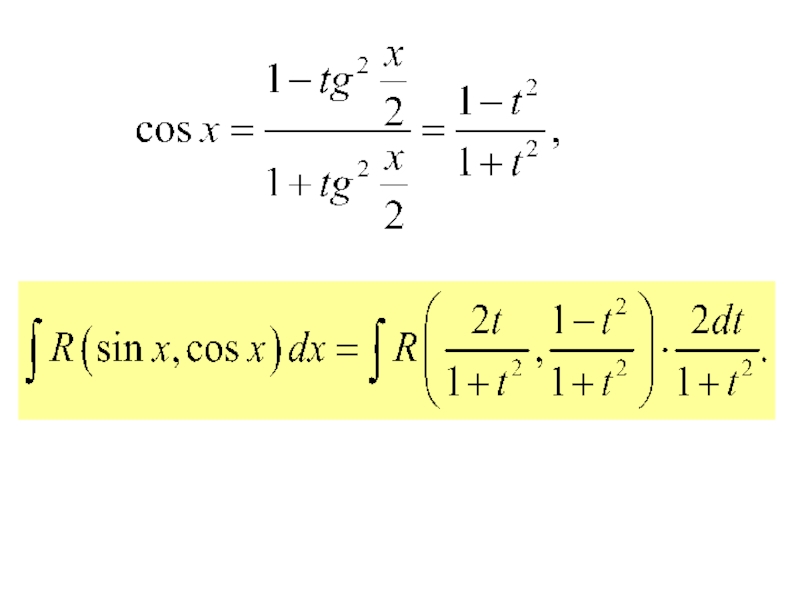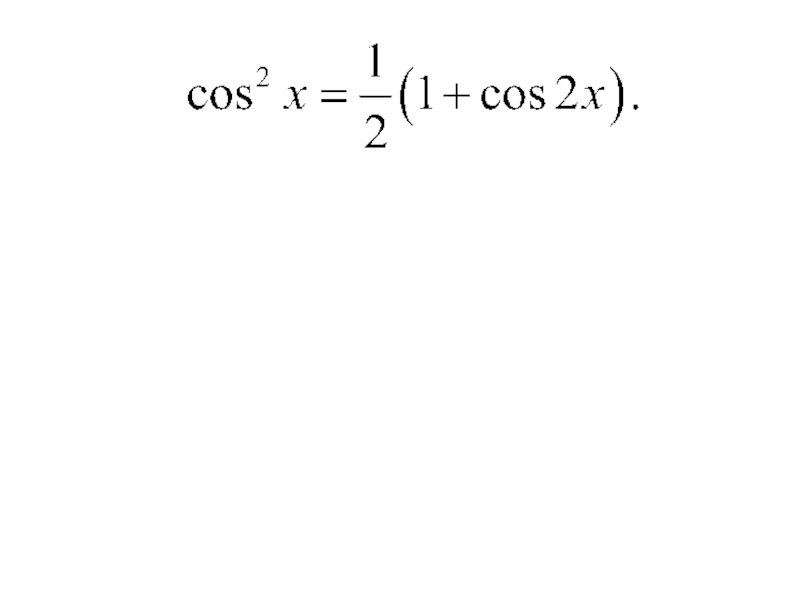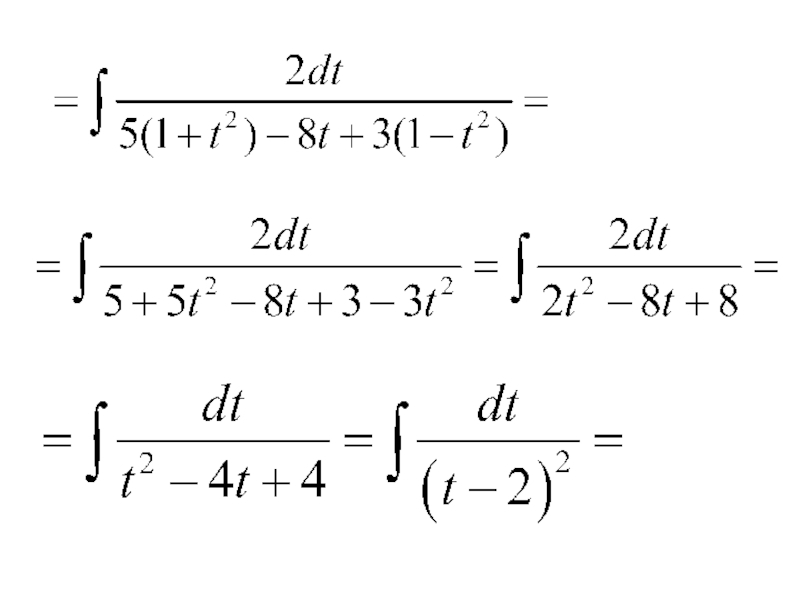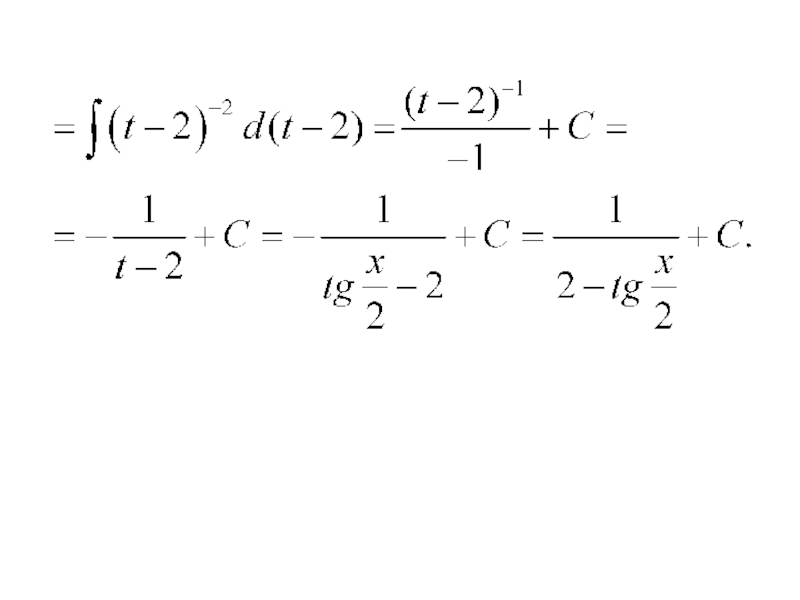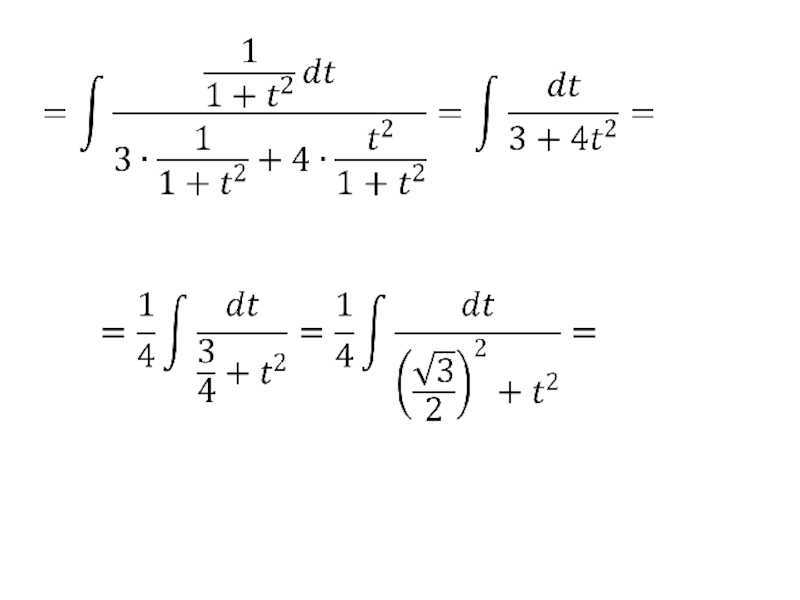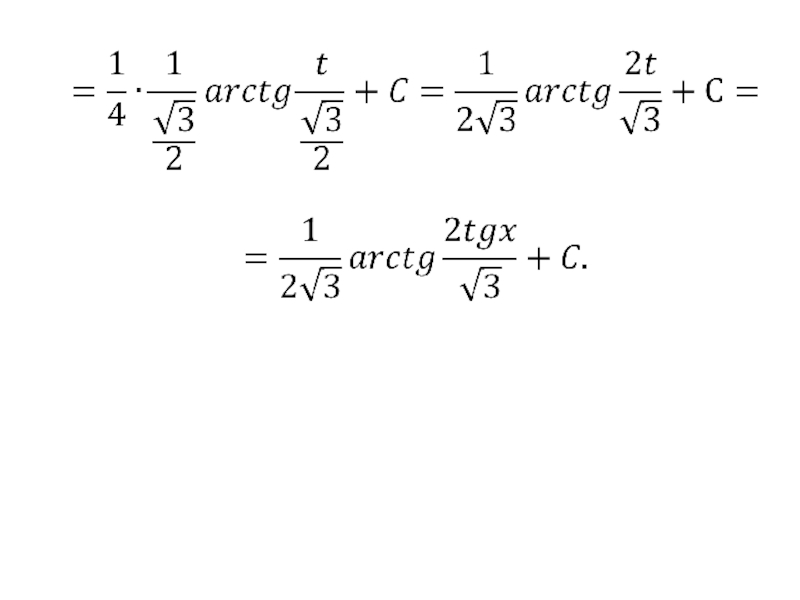- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неопределенный интеграл презентация
Содержание
- 1. Неопределенный интеграл
- 2. §1. Первообразная функции. Неопределенный интеграл и его
- 3. Определение 1. Функция называется
- 4. Пример. Пусть Тогда первообразной для
- 5. Очевидно, что первообразными будут также любые функции где поскольку
- 6. Таким образом, если и
- 7. Определение 2. Множество всех
- 8. Здесь − знак интеграла,
- 9. Нахождение первообразной для данной функции называется
- 10. Геометрически неопределенный интеграл представляет собой семейство кривых,
- 11. Перечислим основные свойства неопределенного интеграла: 1)
- 12. 4) 5) Если
- 13. 6) Если то для
- 14. Приведем таблицу основных неопределенных интегралов: 3) 2) 1)
- 15. 7) 6) 5) 4)
- 16. 11) 10) 9) 8)
- 17. 12) 15) 14) 13)
- 18. Приведенные в данной таблице интегралы называют табличными.
- 19. §2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ. 2.1. Метод
- 20. Примеры. 1)
- 21. 2)
- 22. 3)
- 23. 4)
- 24. 5)
- 26. 6)
- 27. 7)
- 28. 8)
- 30. 2.2. Метод поднесения под знак дифференциала и
- 31. Подведем в этом интеграле множитель
- 33. Следовательно, задача свелась к нахождению интеграла
- 34. Примеры поднесения под знак дифференциала:
- 41. Примеры. 1)
- 42. 2)
- 43. 3)
- 44. 4)
- 45. 5)
- 46. 6)
- 47. 7)
- 48. 8)
- 49. 9)
- 51. 2.3. Метод интегрирования по частям. Пусть
- 52. С помощью этой формулы вычисление интеграла
- 53. При этом в качестве следует
- 54. 1. Интегралы вида
- 55. где − многочлен,
- 56. Тогда формулу (2.1) надо применять столько раз,
- 57. 2. Интегралы вида
- 59. В этом случае соответственно, а
- 60. 3. Интегралы вида Можно положить или
- 61. Примеры. 1)
- 64. 2)
- 66. 2.4. Интегрирование рациональных дробей. Определение. Рациональной
- 67. Если степень многочлена числителя меньше степени
- 68. Простейшей дробью называется правильная дробь одного из
- 69. 5. 4. где
- 70. 2.4.1. Интегрирование простейших рациональных дробей. Интегрирование простейших рациональных дробей рассмотрим на примерах.
- 71. Примеры. 1)
- 72. 2)
- 73. 3) Выделим в знаменателе последнего подынтегрального выражения полный квадрат.
- 74. Тогда
- 75. Вернемся к интегралу:
- 77. 4) В числителе подынтегрального выражения
- 79.
- 80.
- 81. 2.4.2. Интегрирование рациональных дробей с помощью разложения
- 82. 1. Если дана неправильная рациональная дробь, выделить
- 83. 2. Разложить знаменатель дроби на линейные и квадратичные множители: где
- 84. 3. Правильную рациональную дробь разложить на сумму простейших дробей:
- 85.
- 86.
- 87.
- 88. Примеры. 1)
- 89. Тогда
- 90. Итак,
- 92. 2)
- 93.
- 94.
- 95.
- 96.
- 97.
- 98.
- 99.
- 100. 2.5. Интегрирование иррациональных функций. 2.5.1. Квадратичные иррациональности. I. Интегралы вида
- 101. (2.5)
- 102.
- 103. Выделим в подкоренном выражении полный квадрат:
- 104.
- 105.
- 106.
- 107.
- 108.
- 109.
- 110. III. Интегралы вида где
- 111. где
- 112. Пример.
- 115. IV. Интегралы вида где
- 116. где
- 117. Пример.
- 120. IV. Интегралы вида где
- 121. где
- 122. 2.6. Интегрирование тригонометрических выражений. I. Интегралы
- 123. В результате этой подстановки имеем
- 125. Универсальная подстановка во многих
- 126. то применяется подстановка При этом используются формулы
- 127. 2. если − нечетная функция
- 128. 3. если − нечетная функция
- 129. II. Интегралы вида находят
- 130. в) если же и
- 132. Примеры. 1) Так, как
- 133. то будем применять универсальную тригонометрическую подстановку:
- 137.
- 138.
- 139.
- 140.
Слайд 2§1. Первообразная функции. Неопределенный интеграл и его свойства. Таблица основных неопределенных
В дифференциальном исчислении решается задача:
по данной функции
найти ее производную
Интегральное исчисление решает обратную задачу:
найти функцию
если известна ее
производная
Слайд 3Определение 1. Функция
называется
первообразной функции
заданной на
некотором множестве
если для
выполняется равенство
Слайд 7Определение 2. Множество
всех первообразных функции
на множестве
называется неопределенным
и обозначается
Слайд 8Здесь
− знак интеграла,
− подынтегральная функция,
− подынтегральное выражение,
−
Слайд 9Нахождение первообразной для данной функции
называется интегрированием функции
Теорема. Для
функции
существует на этом промежутке
первообразная, а, значит, и неопределенный интеграл.
Слайд 10Геометрически неопределенный интеграл представляет собой семейство кривых, зависящих от одного параметра
которые получаются одна из другой путем
параллельного сдвига вдоль оси
Слайд 19§2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ.
2.1. Метод непосредственного интегрирования.
Непосредственным интегрированием называют
интегрирование с помощью свойств 3, 4 и 6,
тождественных преобразований
подынтегральной функции и таблицы основных
интегралов.
Слайд 302.2. Метод поднесения под знак дифференциала и замены переменной.
На практике
или интегралы, которые сводятся к такому виду
Слайд 31Подведем в этом интеграле множитель
под знак дифференциала:
а затем произведем
В результате получим формулу подстановки в неопределенном интеграле:
Слайд 33Следовательно, задача свелась к нахождению интеграла
который либо уже табличный, либо
Слайд 512.3. Метод интегрирования по частям.
Пусть
и
−
дифференцируемые функции. Тогда справедлива
следующая
(2.1)
Слайд 52С помощью этой формулы вычисление интеграла
сводится к отысканию другого интеграла
Применение формулы целесообразно в тех случаях, когда
интеграл
более прост для нахождения, чем
исходный, либо подобен ему.
Слайд 53При этом в качестве
следует брать такую функцию,
которая при дифференцировании
− ту часть подынтегрального выражения, интеграл
от которого известен или может быть найден. Иногда
формулу (2.1) приходится применяться несколько раз.
Укажем некоторые типы интегралов, которые удобно
вычислять методом интегрирования по частям.
Слайд 662.4. Интегрирование рациональных дробей.
Определение. Рациональной дробью называется функция, заданная в
Слайд 67Если степень многочлена числителя меньше степени
многочлена знаменателя, т.е.
то рациональная дробь
в противном случае, т.е. если
дробь называется неправильной.
Слайд 702.4.1. Интегрирование простейших рациональных дробей.
Интегрирование простейших рациональных дробей рассмотрим на
Слайд 774)
В числителе подынтегрального выражения нужно получить производную знаменателя, т.е.
Тогда
Слайд 812.4.2. Интегрирование рациональных дробей с помощью разложения их на простейшие дроби.
Перед интегрированием рациональной дроби
необходимо выполнить следующие алгебраические преобразования и вычисления:
Слайд 821. Если дана неправильная рациональная дробь, выделить из нее целую часть,
где
− многочлен,
− правильная рациональная дробь.
Слайд 1002.5. Интегрирование иррациональных функций.
2.5.1. Квадратичные иррациональности.
I. Интегралы вида
Слайд 110III. Интегралы вида
где
− рациональная функция,
сводится к интегралу от
помощью подстановки
Слайд 115IV. Интегралы вида
где
− рациональная функция,
сводится к интегралу от
помощью подстановки
Слайд 120IV. Интегралы вида
где
− рациональная функция,
сводится к интегралу от
помощью подстановки
Слайд 1222.6. Интегрирование тригонометрических выражений.
I. Интегралы вида
где
− рациональная функция
и
рациональных функций с помощью универсальной тригонометрической подстановки:
приводятся к интегралам от
Слайд 125Универсальная подстановка
во многих
случаях приводит к сложным вычислениям, поэтому на
1. если
− четная функция
относительно
и
т.е.
Слайд 129II. Интегралы вида
находят
а) при нечетном
с помощью подстановки
б)
с помощью подстановки
Слайд 130в) если же
и
− четные, то подынтегральную
функцию необходимо преобразовать с