Преобразование Фурье презентация

Содержание

1. Преобразование Фурье
2. ПЛАН Обобщенный ряд Фурье Тригонометрический ряд Фурье
3. ЛИТЕРАТУРА Поршнев С.В., Беленкова И.В., Численные методы
4. Периодическая функция с периодом Обобщенный ряд
5. Разложение периодических функций в обобщенный ряд Фурье
6. Тригонометрический ряд Фурье Тригонометрический базис Тригонометрический ряд
7. коэффициенты Фурье Тригонометрический ряд Фурье
8. коэффициенты Фурье Вывод выражений
9. Частоты гармоник ряда Фурье основная частота
10. Четные и нечетные функции Периодическая
11. Равенство Парсеваля для ряда Фурье
12. Амплитуды и фазы гармоник гармоника ряда Фурье
13. Ряд Фурье по комплексным экспонентам
14. Ряд Фурье по комплексным экспонентам Соотношения для вещественной периодической функции
15. Ряд Фурье по комплексным экспонентам Замечание. Отрицательная
16. Преобразование Фурье для непериодических функций комплексная амплитуда
17. Преобразование Фурье. Интеграл Фурье
18. Прямое преобразование Фурье Интеграл Фурье Обратное преобразование Фурье - функции, сопряженные по Фурье
19. Условия существования интеграла Фурье Функция должна быть
20. Основные свойства преобразования Фурье 1. Взаимная однозначность
21. Основные свойства преобразования Фурье 4. Теорема
22. Основные свойства преобразования Фурье 5. Теорема Парсеваля для интеграла Фурье Равенство Парсеваля
23. Основные свойства преобразования Фурье 6. Дельта-функция и
24. Теорема отсчетов 1935 г. В.А. Котельников;
25. Доказательство теоремы отсчетов доопределили функцию
26. Доказательство теоремы отсчетов. Ряд Котельникова. Число степеней
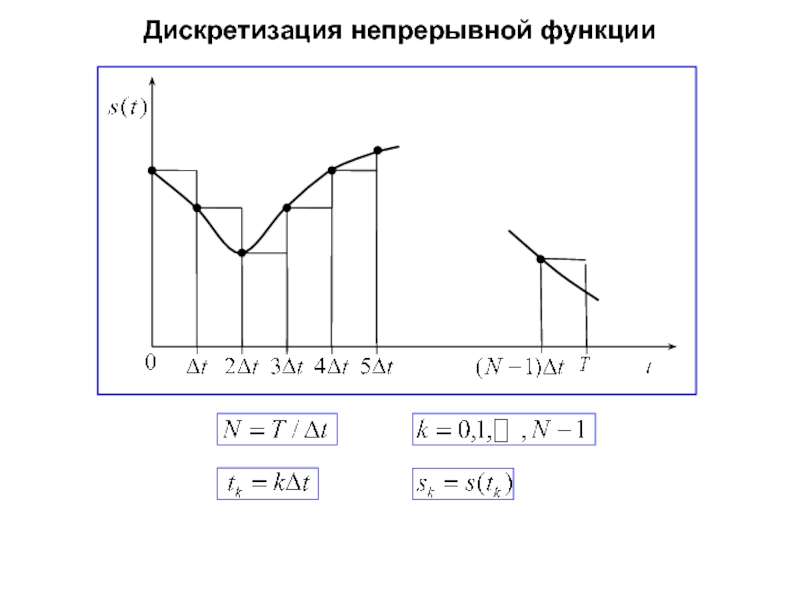
27. Дискретизация непрерывной функции
28. Численный спектральный анализ Получить самостоятельно выражения для
29. Численный спектральный анализ интегральная сумма
30. Дискретное преобразование Фурье комплексный коэффициент
31. Свойства ДПФ Линейность Число коэффициентов ДПФ равно
32. Если - дискретная последовательность вещественных чисел, то
33. Если - дискретная последовательность вещественных чисел, то
34. Периодическое продолжение дискретной последовательности Свойства ДПФ обратное ДПФ
35. Частоты ДПФ положительные частоты отрицательные частоты максимальная
36. Пример с перестановкой частот комплексного спектра ДПФ
37. Двумерное ДПФ прямое двумерное
38. Быстрое преобразование Фурье Быстрое преобразование Фурье
39. Быстрое преобразование Фурье
40. Быстрое преобразование Фурье
41. Cредства Mathcad для реализации ДПФ и БПФ
42. Сходимость ряда Фурье Пусть s(t) – кусочно
43. Скорость сходимости ряда Фурье Скорость сходимости
44. Эффект Гиббса Явление Гиббса: неравномерная сходимость ряда
45. Эффект Гиббса. Пример
46. Сглаживание пульсаций. Сигма-факторы Методика сглаживания К.
47. Сглаживание пульсаций. Сигма-факторы Методика сглаживания К. Ланцоша
48. Сглаживание пульсаций. Пример

ПЛАН Обобщенный ряд Фурье Тригонометрический ряд Фурье Понятие о спектре периодической функции Преобразование Фурье для непериодических функций. Интеграл Фурье Основные математические свойства преобразования Фурье Теорема отсчетов Дискретное преобразование Фурье Свойства дискретного

Слайд 1Модуль 1. Тема 1 Преобразование Фурье

Слайд 2ПЛАН
Обобщенный ряд Фурье
Тригонометрический ряд Фурье
Понятие о спектре периодической функции
Преобразование Фурье для

непериодических функций. Интеграл Фурье
Основные математические свойства преобразования Фурье
Теорема отсчетов
Дискретное преобразование Фурье
Свойства дискретного преобразования Фурье
Быстрое преобразование Фурье
Сходимость ряда Фурье. Эффект Гиббса. Сглаживание высокочастотных пульсаций. Сигма-факторы.

Слайд 3ЛИТЕРАТУРА
Поршнев С.В., Беленкова И.В., Численные методы на базе Mathcad. – СПб.:

БХВ-Петербург, 2005, – 464 с.
Зверев В.А., Стромков А.А., Выделение сигналов из помех численными методами. - Нижний Новгород: ИПФ РАН, 2001, - 188 с.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М., Численные методы. - М.: Бином. Лаборатория знаний, 2004, - 640 с.
Ханова А.А., Макарова И.Г., Лабораторный практикум по математическому моделированию и методам в расчетах на ЭВМ. – Интернет-ресурс: http://exponenta.ru/educat/systemat/hanova/lab/lr.asp

Слайд 4Периодическая функция с периодом
Обобщенный ряд Фурье для периодической функции
Скалярное произведение

Ортонормированный

базис

Условие взаимной ортогональности
Условие нормировки

Комплексное сопряжение

Система функций

Слайд 5Разложение периодических функций в обобщенный ряд Фурье

- обобщенный ряд Фурье для

периодической функции

В результате имеем выражение для коэффициентов ряда :

Рассмотрим скалярное произведение функции и базисной функции:

Слайд 6Тригонометрический ряд Фурье
Тригонометрический
базис
Тригонометрический
ряд Фурье
Условия разложимости периодической функции в ряд Фурье
Функция должна

быть абсолютно интегрируема, т.е. должен существовать интеграл

Функция должна иметь только конечное число разрывов первого рода и конечное число максимумов и минимумов в пределах одного периода
Функция не должна иметь разрывов второго рода

Слайд 7коэффициенты Фурье
Тригонометрический ряд Фурье

Слайд 8

коэффициенты Фурье

Вывод выражений для коэффициентов Фурье
Тригонометрический ряд Фурье
Остальные выражения получаются аналогично
Скалярное

произведение с базисной функцией

Слагаемое ряда Фурье

Слайд 9Частоты гармоник ряда Фурье

основная частота – циклическая частота, соответствующая периоду функции
постоянная

составляющая =
среднее значение функции за период

ряд Фурье

Постоянная составляющая ряда Фурье

Слайд 10

Четные и нечетные функции
Периодическая функция с периодом
Ряд Фурье
Четная функция
Нечетная функция

Слайд 11Равенство Парсеваля для ряда Фурье

ряд Фурье
Равенство Парсеваля
Равенство Парсеваля связывает
энергию сигнала

во временной области
с коэффициентами Фурье

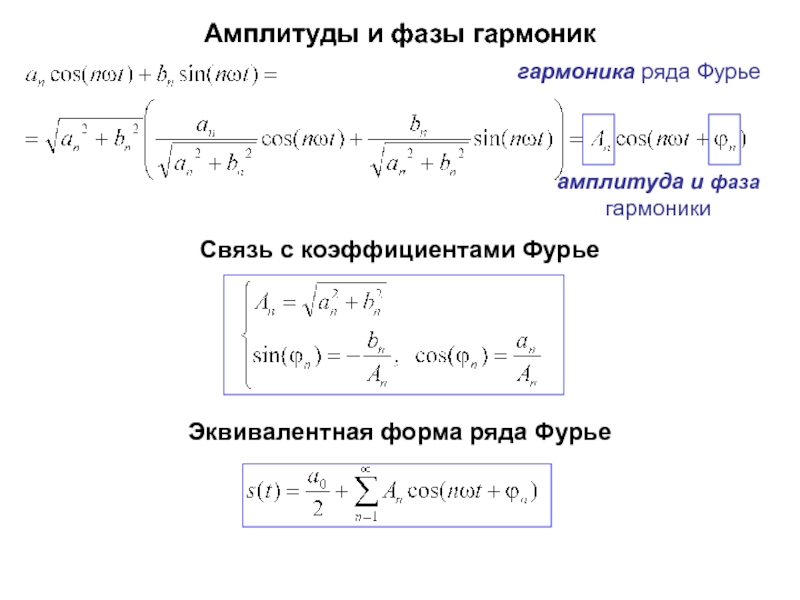
Слайд 12Амплитуды и фазы гармоник
гармоника ряда Фурье

амплитуда и фаза
гармоники
Связь с коэффициентами Фурье

Эквивалентная

форма ряда Фурье

Слайд 13Ряд Фурье по комплексным экспонентам

Слайд 14Ряд Фурье по комплексным экспонентам

Соотношения для вещественной периодической функции

Слайд 15Ряд Фурье по комплексным экспонентам
Замечание. Отрицательная частота является не физическим, а

математическим понятием, вытекающим из способа представления комплексных чисел

ряд Фурье

формула для расчета
комплексной амплитуды
гармоники

Слайд 16Преобразование Фурье для непериодических функций
комплексная амплитуда
гармоники
Непериодическая функция может рассматриваться как

функция с бесконечно большим периодом => нужен предельный переход

Расстояние между соседними отсчетами в частотной области

ряд Фурье

новая функция

Слайд 17Преобразование Фурье. Интеграл Фурье

Здесь частоту нельзя определить, как величину, обратную периоду.

Частотой теперь будем называть новую непрерывную независимую переменную, которая появилась в формулах для интеграла Фурье

Слайд 18

Прямое преобразование Фурье
Интеграл Фурье
Обратное преобразование Фурье
- функции, сопряженные по Фурье

Слайд 19Условия существования интеграла Фурье
Функция должна быть абсолютно интегрируема, т.е. должен существовать

интеграл

Функция должна иметь только конечное число разрывов первого рода и конечное число максимумов и минимумов в пределах любого отрезка конечных размеров
Функция не должна иметь разрывов второго рода

Для функций, которые не удовлетворяют условиям существования, часто можно найти имеющее смысл преобразование, если эти функции удается определить как предел последовательности функций, поддающихся преобразованию Фурье. Преобразуя каждый член определяющей последовательности, мы получаем соответствующую последовательность Фурье-образов, предел которой называется обобщенным Фурье-образом исходной функции.

Слайд 20Основные свойства преобразования Фурье
1. Взаимная однозначность

2. Линейность

3. Теорема смещения

Слайд 21Основные свойства преобразования Фурье

4. Теорема о свертке

Прямая теорема: преобразование Фурье от

свертки двух функций равно произведению преобразований Фурье от этих функций

Обратная теорема: преобразование Фурье от произведения функций равно свертке их преобразований Фурье

Слайд 22Основные свойства преобразования Фурье
5. Теорема Парсеваля для интеграла Фурье

Равенство Парсеваля

Слайд 23Основные свойства преобразования Фурье
6. Дельта-функция и функция Хевисайда

Дельта-функция
Функция Хевисайда (ступенька)

Слайд 24Теорема отсчетов
1935 г. В.А. Котельников; 1945 г. Клод Шенон;

1915 г. Уиттекер

Функция с ограниченным спектром - функция, спектр которой по модулю обращается в нуль на всех частотах, начиная с частоты :

Непрерывная функция, имеющая ограниченный спектр, может быть представлена в любой точке на основании своих значений, взятых
в дискретных точках отсчета. При этом на период колебаний на граничной частоте должно приходиться не менее двух точек отсчета:

- расстояние между точками отсчета

Слайд 25Доказательство теоремы отсчетов

доопределили функцию
как периодическую

применили обратное преобразование Фурье
применили обратную теорему

о свертке

ограничение ширины спектра выделили явно

новая функция

Слайд 26Доказательство теоремы отсчетов. Ряд Котельникова. Число степеней свободы функции

Ряд Котельникова позволяет вычислить

с любой точностью значения непрерывной функции по ее значениям в дискретных точках отсчета

Число степеней свободы функции

- ширина спектра и длина области задания финитной функции

Слайд 27
Дискретизация непрерывной функции

Слайд 28Численный спектральный анализ
Получить самостоятельно выражения для численного расчета интегралов, применив левостороннюю

формулу прямоугольников

В окончательную формулу длина промежутка дискретизации
должна не входить

Слайд 29Численный спектральный анализ

интегральная сумма
по левосторонней формуле прямоугольников

формулы для численного расчета

коэффициентов Фурье

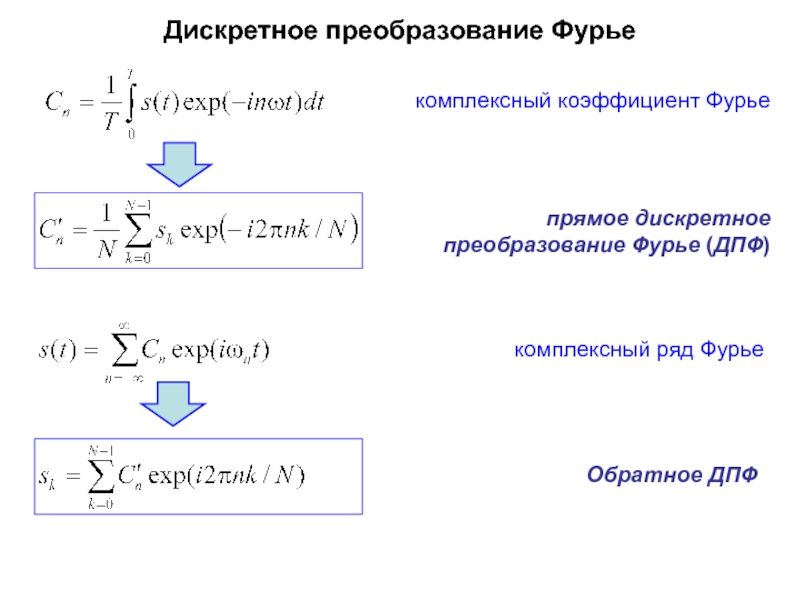
Слайд 30Дискретное преобразование Фурье

комплексный коэффициент Фурье
прямое дискретное преобразование Фурье (ДПФ)

Обратное ДПФ
комплексный ряд

Фурье

Слайд 31Свойства ДПФ
Линейность
Число коэффициентов ДПФ равно числу N элементов исходной последовательности
Постоянная составляющая

(коэффициент с номером нуль) есть среднее значение дискретной последовательности:

Если N - четное, то

Слайд 32Если - дискретная последовательность вещественных чисел, то имеет место равенство

Свойства ДПФ

комплексное

сопряжение

Слайд 33Если - дискретная последовательность вещественных чисел, то имеет место равенство

поэтому можно

считать, что вторая половина коэффициентов

отвечает отрицательным частотам, для которых по свойствам комплексных амплитуд

Свойства ДПФ

комплексное сопряжение

Слайд 34Периодическое продолжение дискретной последовательности
Свойства ДПФ
обратное ДПФ

Слайд 35Частоты ДПФ
положительные частоты
отрицательные частоты
максимальная частота
Пусть последовательность из отсчетов

является дискретным представлением непрерывной функции на промежутке . Тогда

Если ДПФ рассматривается как преобразование дискретного набора данных и речи о дискретизации непрерывной функции не идет, то при определении частот полагают период последовательности
(последовательность периодична по номерам элементов с периодом )

условие точного соответствия ДПФ непрерывному преобразованию Фурье

Слайд 36Пример с перестановкой частот комплексного спектра ДПФ

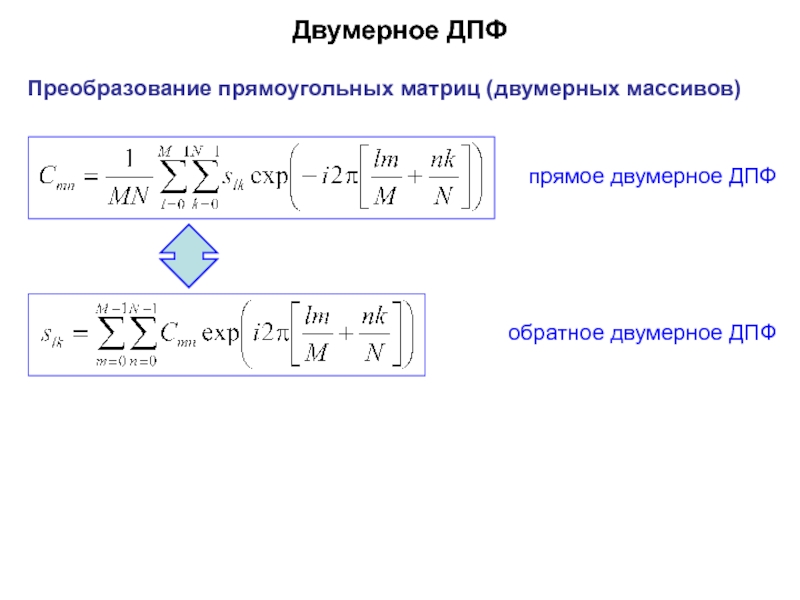
Слайд 37Двумерное ДПФ

прямое двумерное ДПФ
обратное двумерное ДПФ
Преобразование прямоугольных матриц (двумерных массивов)

Слайд 38Быстрое преобразование Фурье

Быстрое преобразование Фурье (БПФ) - “быстрый” алгоритм расчета ДПФ

Слайд 39Быстрое преобразование Фурье

Слайд 40Быстрое преобразование Фурье

Порядок сложности алгоритма БПФ

Порядок сложности алгоритма ДПФ

Слайд 41Cредства Mathcad для реализации ДПФ и БПФ
Встроенные функции (пары функций) –

см. описания в справочной системе

fft, ifft – Fast Fourier Transform (FFT), Inverse FFT
FFT, IFFT

cfft, icfft – Complex FFT, Inverse Complex FFT
CFFT, ICFFT

Готовые примеры (quicksheets):

Engineering Applications\Fast Fourier Transforms
qsheet\Applications\f060.xmcd
Calculus and DiffEQs\Fourier Coefficients: Signal Generation
qsheet\Calculus_Des\fourcoef.xmcd

Слайд 42Сходимость ряда Фурье
Пусть s(t) – кусочно непрерывно дифференцируемая функция с периодом

T. Тогда ряд Фурье функции s(t) сходится в каждой точке отрезка [0,T]:

Ряд Фурье

равенство верно для любой точки

равенство в точке непрерывности

Слайд 43
Скорость сходимости ряда Фурье
Скорость сходимости ряда Фурье функции s(t) зависит от

ее гладкости - количества непрерывных производных.

Теорема. Если s(t) непрерывно дифференцируема r раз на отрезке [0,T], то для частичных сумм ряда Фурье sN(t) справедливы неравенства:

частичная сумма
ряда Фурье

неравенство для
среднеквадратического
отклонения

Слайд 44Эффект Гиббса
Явление Гиббса: неравномерная сходимость ряда Фурье функции s(t) с периодом

T в точках разрыва.

значение ряда Фурье в точке разрыва t '

Использование конечного числа членов ряда Фурье для функций с разрывами, например при численном моделировании, приводит к тому, что частичные суммы ряда содержат периодические функции, период которых равен периоду последнего удержанного члена .

Слайд 45Эффект Гиббса. Пример

Слайд 46Сглаживание пульсаций. Сигма-факторы

Методика сглаживания К. Ланцоша – усреднение частичных сумм ряда

Фурье по периоду последнего оставленного или первого отброшенного члена

Слайд 47Сглаживание пульсаций. Сигма-факторы
Методика сглаживания К. Ланцоша – усреднение частичных сумм ряда

Фурье по периоду последнего оставленного или первого отброшенного члена

коэффициенты Фурье домножаются
на сигма-факторы

Слайд 48Сглаживание пульсаций. Пример

Скачать презентацию

Преобразование Фурье презентация

Содержание

Слайд 1Модуль 1. Тема 1 Преобразование Фурье

Слайд 2ПЛАНОбобщенный ряд ФурьеТригонометрический ряд ФурьеПонятие о спектре периодической функцииПреобразование Фурье для

Слайд 3ЛИТЕРАТУРАПоршнев С.В., Беленкова И.В., Численные методы на базе Mathcad. – СПб.:

Слайд 4Периодическая функция с периодом Обобщенный ряд Фурье для периодической функцииСкалярное произведениеОртонормированный

Слайд 5Разложение периодических функций в обобщенный ряд Фурье- обобщенный ряд Фурье для

Слайд 6Тригонометрический ряд ФурьеТригонометрическийбазисТригонометрическийряд ФурьеУсловия разложимости периодической функции в ряд ФурьеФункция должна

Слайд 7коэффициенты ФурьеТригонометрический ряд Фурье

Слайд 8коэффициенты ФурьеВывод выражений для коэффициентов ФурьеТригонометрический ряд ФурьеОстальные выражения получаются аналогичноСкалярное

Слайд 9Частоты гармоник ряда Фурьеосновная частота – циклическая частота, соответствующая периоду функциипостоянная

Слайд 10Четные и нечетные функцииПериодическая функция с периодом Ряд ФурьеЧетная функцияНечетная функция

Слайд 11Равенство Парсеваля для ряда Фурьеряд ФурьеРавенство ПарсеваляРавенство Парсеваля связывает энергию сигнала

Слайд 12Амплитуды и фазы гармоникгармоника ряда Фурьеамплитуда и фазагармоникиСвязь с коэффициентами ФурьеЭквивалентная

Слайд 13Ряд Фурье по комплексным экспонентам

Слайд 14Ряд Фурье по комплексным экспонентамСоотношения для вещественной периодической функции

Слайд 15Ряд Фурье по комплексным экспонентамЗамечание. Отрицательная частота является не физическим, а

Слайд 16Преобразование Фурье для непериодических функцийкомплексная амплитуда гармоникиНепериодическая функция может рассматриваться как

Слайд 17Преобразование Фурье. Интеграл ФурьеЗдесь частоту нельзя определить, как величину, обратную периоду.

Слайд 18Прямое преобразование ФурьеИнтеграл ФурьеОбратное преобразование Фурье- функции, сопряженные по Фурье

Слайд 19Условия существования интеграла ФурьеФункция должна быть абсолютно интегрируема, т.е. должен существовать

Слайд 20Основные свойства преобразования Фурье1. Взаимная однозначность2. Линейность3. Теорема смещения

Слайд 21Основные свойства преобразования Фурье4. Теорема о сверткеПрямая теорема: преобразование Фурье от

Слайд 22Основные свойства преобразования Фурье5. Теорема Парсеваля для интеграла ФурьеРавенство Парсеваля

Слайд 23Основные свойства преобразования Фурье6. Дельта-функция и функция ХевисайдаДельта-функцияФункция Хевисайда (ступенька)

Слайд 24Теорема отсчетов1935 г. В.А. Котельников; 1945 г. Клод Шенон;

Слайд 25Доказательство теоремы отсчетовдоопределили функцию как периодическуюприменили обратное преобразование Фурьеприменили обратную теорему

Слайд 26Доказательство теоремы отсчетов. Ряд Котельникова. Число степеней свободы функцииРяд Котельникова позволяет вычислить

Слайд 27Дискретизация непрерывной функции

Слайд 28Численный спектральный анализПолучить самостоятельно выражения для численного расчета интегралов, применив левостороннюю

Слайд 29Численный спектральный анализинтегральная сумма по левосторонней формуле прямоугольниковформулы для численного расчета

Слайд 30Дискретное преобразование Фурьекомплексный коэффициент Фурьепрямое дискретное преобразование Фурье (ДПФ)Обратное ДПФкомплексный ряд

Слайд 31Свойства ДПФЛинейностьЧисло коэффициентов ДПФ равно числу N элементов исходной последовательностиПостоянная составляющая

Слайд 32Если - дискретная последовательность вещественных чисел, то имеет место равенствоСвойства ДПФкомплексное

Слайд 33Если - дискретная последовательность вещественных чисел, то имеет место равенство поэтому можно

Слайд 34Периодическое продолжение дискретной последовательностиСвойства ДПФобратное ДПФ

Слайд 35Частоты ДПФположительные частотыотрицательные частотымаксимальная частотаПусть последовательность из отсчетов