- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движение в пространстве. (10 класс) презентация
Содержание
- 1. Движение в пространстве. (10 класс)
- 2. Движение в пространстве. Преобразование, при котором сохраняются
- 3. Параллельный перенос в пространстве. Преобразование, при котором
- 4. Свойства параллельного переноса. Параллельный перенос есть движение.
- 6. Подобие пространственных фигур. Преобразование фигуры F называется
- 8. Гомотетия. Гомотетия относительно центра О с коэффициентом
Слайд 2Движение в пространстве.
Преобразование, при котором сохраняются расстояния между точками, называется движением.
Свойства:
при движении в пространстве прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, плоскости – в плоскости; сохраняются углы между полупрямыми.
Две фигуры называются равными, если они совмещаются движением.
Две фигуры называются равными, если они совмещаются движением.
Слайд 3Параллельный перенос в пространстве.
Преобразование, при котором произвольная точка (х; у; z)
фигуры переходит в точку (х+а; у+в; z+с), где числа а, в, с одни и те же для всех точек (х; у; z) , называется параллельным переносом.
Задается формулами: х’= х+а
у’= у+в
z’ = z+c
Задается формулами: х’= х+а
у’= у+в
z’ = z+c
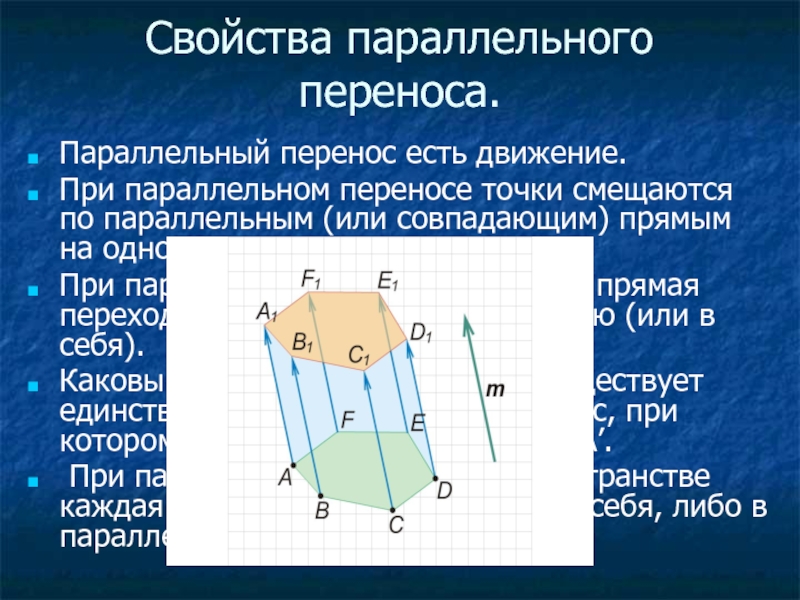
Слайд 4Свойства параллельного переноса.
Параллельный перенос есть движение.
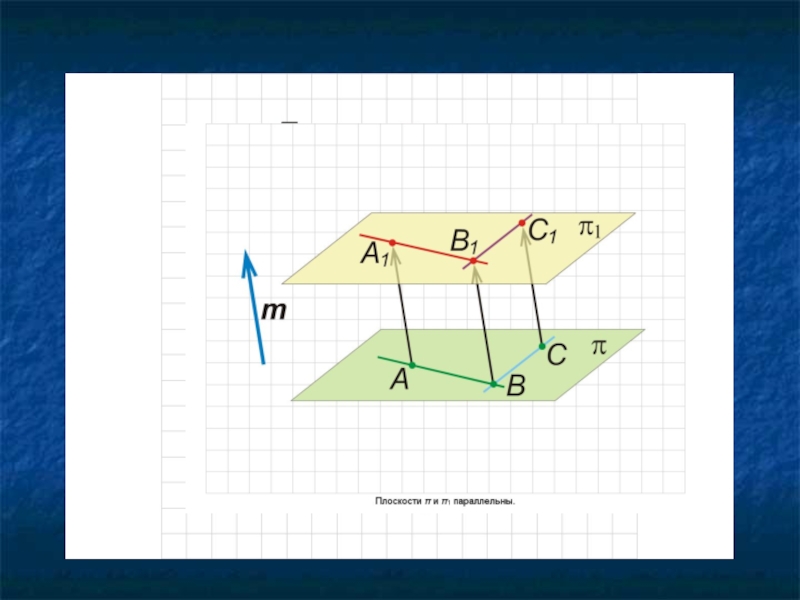
При параллельном переносе точки смещаются по
параллельным (или совпадающим) прямым на одно и то же расстояние.
При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
Каковы бы ни были точки А и А’, существует единственный параллельный перенос, при котором точка А переходит в точку А’.
При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.
При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
Каковы бы ни были точки А и А’, существует единственный параллельный перенос, при котором точка А переходит в точку А’.
При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.
Слайд 6Подобие пространственных фигур.
Преобразование фигуры F называется преобразованием подобия, если при этом
преобразовании расстояния между точками изменяются в одно и то же число раз.
Для любых двух точек X’, Y’ фигуры F’, в которые они переходят, X’Y’ = k XY.
Две фигуры называются подобными, если они переводятся одна в другую преобразованием подобия.
Для любых двух точек X’, Y’ фигуры F’, в которые они переходят, X’Y’ = k XY.
Две фигуры называются подобными, если они переводятся одна в другую преобразованием подобия.
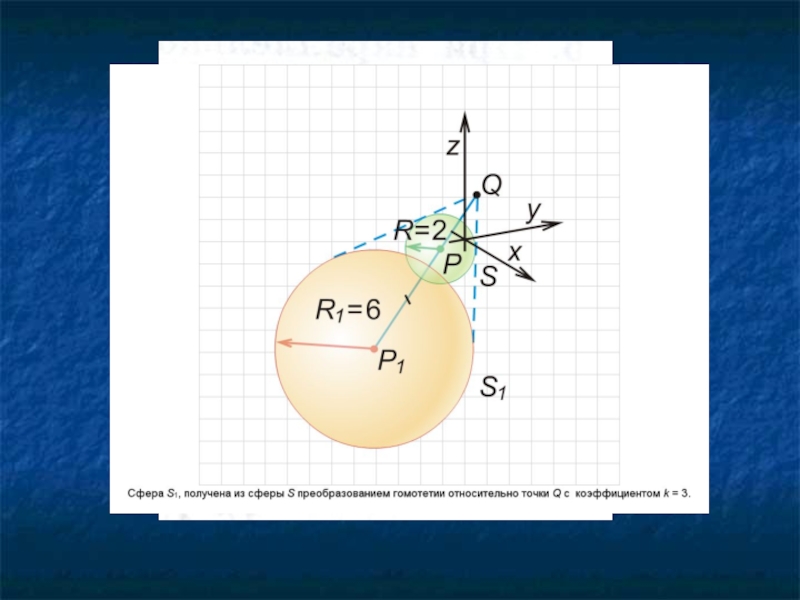
Слайд 8Гомотетия.
Гомотетия относительно центра О с коэффициентом гомотетии k – это преобразование,
которое переводит произвольную точку Х в точку Х’ луча ОХ, такую, что ОХ’ = k ОХ.
Преобразование гомотетии в пространстве переводит любую плоскость, не проходящую через центр гомотетии, в параллельную плоскость (или в себя при k=1)
Преобразование гомотетии в пространстве переводит любую плоскость, не проходящую через центр гомотетии, в параллельную плоскость (или в себя при k=1)