Пределы презентация

Содержание

1. Пределы
2. Бесконечной числовой последовательностью называется числовая функция, определённая на множестве натуральных чисел.
3. Способы задания последовательности: 1) В виде формулы
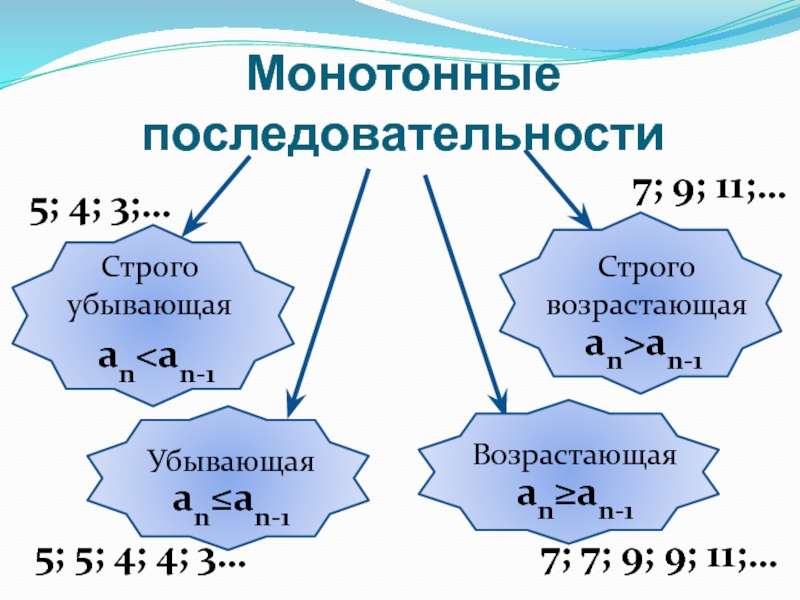
4. Монотонные последовательности Строго убывающая anan-1
5. Знакочередующаяся последовательность
6. Последовательность an называется ограниченной, если существуют такие
7. Если существует точка М (m), и не
8. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ. Число а называют пределом
9. Последовательность, имеющая предел, называется сходящейся, а не
10. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ. Бесконечно
11. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ. Последовательность называется
12. Свойства бесконечно малой. Сумма и произведение конечного
13. Свойства пределов.
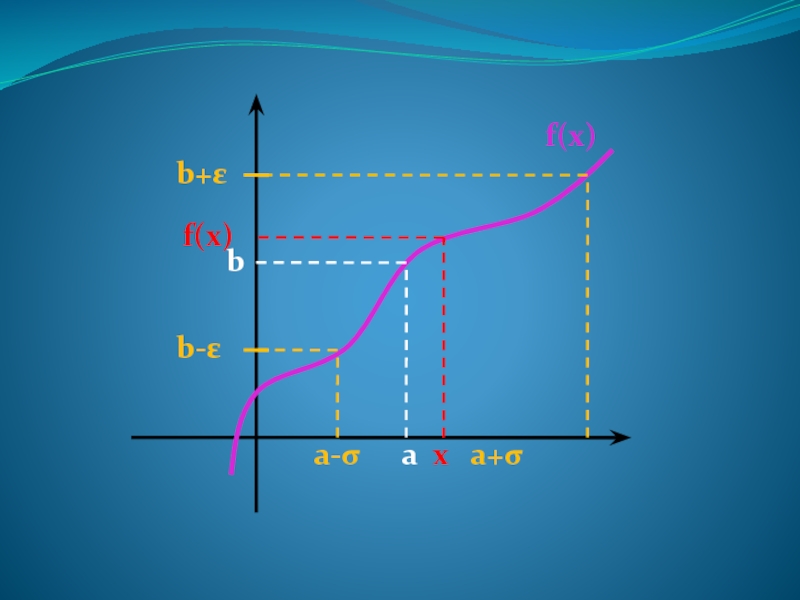
14. Предел функции Число b есть предел функции
15. a b b-ε b+ε a-σ a+σ x f(x) f(x)
16. Теоремы о пределах 6) Правило Лопиталя: Теоремы 2-5 см свойства пределов последовательности
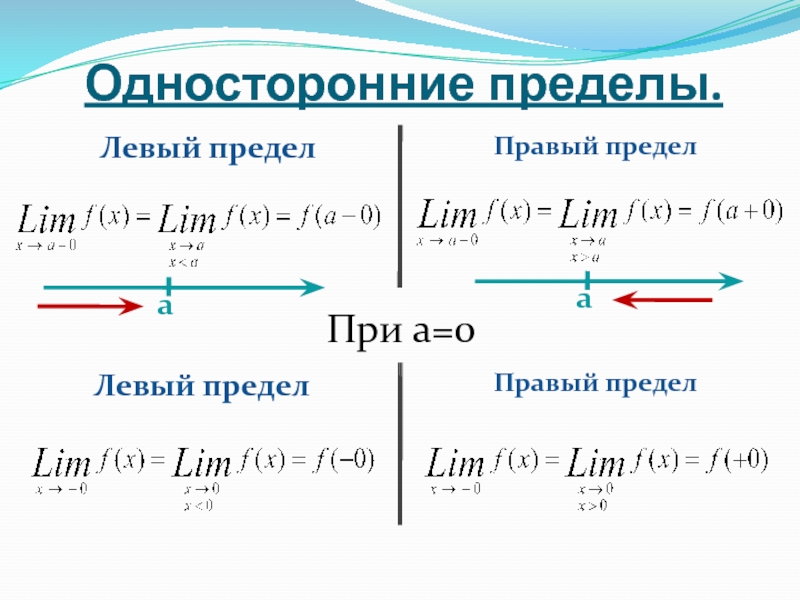
17. Односторонние пределы. Левый предел Правый предел
18. Найти предел функции при x →1 Левый предел: Правый предел:
19. Замечательные пределы Две бесконечно малые называются эквивалентными,
20. Замечательные пределы
21. Эквивалентные функции при x → 0 sin
22. Если предел отношения двух бесконечно малых равен
23. Непрерывная функция ТЕОРЕМА: Функция не может
24. Функция, непрерывная в каждой точке промежутка называется
25. Свойства непрерывных функций ТЕОРЕМА 1 , 2

Бесконечной числовой последовательностью называется числовая функция, определённая на множестве натуральных чисел.

Слайд 1Числовые последовательности
Предел числовой последовательности и её сходимость

Слайд 2Бесконечной числовой последовательностью называется числовая функция, определённая на множестве натуральных чисел.

Слайд 3Способы задания последовательности:
1) В виде формулы – по номеру n-ого члена
an=2n
2)

Рекуррентный (индуктивный) –

указывается правило, по которому можно вычислить общий член последовательности через предыдущие и задается несколько первых членов.

an=an-1+an-2 a1=3, a2=5,

3) Словесное описание последовательности

Слайд 4Монотонные последовательности

Строго убывающая
anan-1

Возрастающая
an≥an-1
5; 4; 3;…
5; 5; 4; 4; 3…
7; 9;

11;…

7; 7; 9; 9; 11;…

Слайд 5Знакочередующаяся последовательность

Слайд 6Последовательность an называется ограниченной, если существуют такие точки M и m,

что для любого натурального n выполняется неравенство: m≤an≤M

В противном случае последовательность называется
неограниченной.

Слайд 7Если существует точка М (m), и не существует точка m (M),

то последовательность называется ограниченной сверху (снизу) и неограниченной снизу (сверху).

- ограниченна снизу

- ограниченна сверху

Слайд 8ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ.
Число а называют пределом числовой последовательности, если для любого

положительного ε > 0 существует такое натуральное N, что для каждого натурального n ≥ N выполняется неравенство |an-a|<ε

a-ε

a+ε

Слайд 9Последовательность, имеющая предел, называется сходящейся, а не имеющая предел – расходящейся.
ТЕОРЕМА:

Необходимое условие существования предела последовательности.

Если последовательность имеет предел, то она ограничена.

ТЕОРЕМА 1: Всякая сходящаяся последовательность имеет один предел.

ТЕОРЕМА 2: Если числовая последовательность монотонна и ограничена, то она имеет предел.

Слайд 10БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ.
Бесконечно малой (бм) величиной называется такая

переменная величина, которая в процессе своего изменения становится и в дальнейшем остается по модулю меньше любого наперед заданного положительного числа, как бы мало оно ни было.

Слайд 11БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ.
Последовательность называется бесконечно большой (бб), если для

каждого положительного числа А найдется такое натуральное число N, что для любого n >N выполняется неравенство: |an|>A

Слайд 12Свойства бесконечно малой.
Сумма и произведение конечного числа бесконечно малых последовательностей есть

бесконечно малая последовательность.
Произведение константы на бесконечно малую последовательность есть бесконечно малая последовательность.
x – бесконечно малая, то 1/x – бесконечно большая и наоборот (x – бб → 1/x – бм).

Если

то

Если

то

Слайд 13Свойства пределов.

Слайд 14Предел функции
Число b есть предел функции f(x) при x→a если, какова

бы ни была ε-окрестность точки b, найдется такая σ-окрестность точки а, что для любого значения x≠a и принадлежащего σ-окрестности точки а, значение f(x) ,будет принадлежать ε-окрестности точки b.

Слайд 15
a
b
b-ε
b+ε
a-σ
a+σ
x
f(x)
f(x)

Слайд 16Теоремы о пределах

6) Правило Лопиталя:
Теоремы 2-5 см свойства пределов последовательности

Слайд 17Односторонние пределы.
Левый предел
Правый предел

При a=0
Левый предел
Правый предел

a
a

Слайд 18Найти предел функции при x →1
Левый предел:

Правый предел:

Слайд 19Замечательные пределы
Две бесконечно малые называются эквивалентными, если предел их отношения равен

единице.

Эквивалентные бесконечно малые можно заменять одна на другую.

Слайд 20Замечательные пределы

Слайд 21Эквивалентные функции при x → 0
sin x ~ x
tg x ~

x
arcsin x ~ x
arctg x ~ x
ex – 1 ~ x
ln (1 + x) ~ x
(1 + x)k – 1 ~ k x

Слайд 22Если предел отношения двух бесконечно малых равен некоторому числу k, отличному

от единицы, то эти бесконечно малые называются одинаковыми или бесконечно малыми одного порядка малости.

Если предел отношения двух бесконечно малых равен нулю, то в числителе бесконечно малая более высокого порядка, чем в знаменателе.

Слайд 23Непрерывная функция
ТЕОРЕМА: Функция не может иметь двух различных пределов в

точке.

Функция является непрерывной в точке а, если она имеет предел равный значению функции в этой точке.

Слайд 24Функция, непрерывная в каждой точке промежутка называется непрерывной на всём промежутке.
Точки,

в которых нарушается непрерывность функции, называются точками разрыва этой функции.

Функция, имеющая правый (левый) предел, непрерывна справа (слева).

Если функция имеет конечный правый или левый предел в точке разрыва, то это – точка разрыва первого рода (все остальные – второго рода).

Слайд 25Свойства непрерывных функций
ТЕОРЕМА 1 , 2 Сумма (произведение) конечного числа непрерывных

в точке а функций есть непрерывная в этой точке функция.

ТЕОРЕМА 3 Отношение двух функций, непрерывных в точке а есть непрерывная в этой точке функция, если значение функции, стоящей в знаменателе в точке а отлично от нуля.

Скачать презентацию

Пределы презентация

Содержание

Слайд 1Числовые последовательности
Предел числовой последовательности и её сходимость

Слайд 2Бесконечной числовой последовательностью называется числовая функция, определённая на множестве натуральных чисел.

Слайд 3Способы задания последовательности:
1) В виде формулы – по номеру n-ого члена
an=2n
2)

Слайд 4Монотонные последовательности

Строго убывающая
anan-1

Возрастающая
an≥an-1
5; 4; 3;…
5; 5; 4; 4; 3…
7; 9;

Слайд 5Знакочередующаяся последовательность

Слайд 6Последовательность an называется ограниченной, если существуют такие точки M и m,

Слайд 7Если существует точка М (m), и не существует точка m (M),

Слайд 8ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ.
Число а называют пределом числовой последовательности, если для любого

Слайд 9Последовательность, имеющая предел, называется сходящейся, а не имеющая предел – расходящейся.
ТЕОРЕМА:

Слайд 10БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ.
Бесконечно малой (бм) величиной называется такая

Слайд 11БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ.
Последовательность называется бесконечно большой (бб), если для

Слайд 12Свойства бесконечно малой.
Сумма и произведение конечного числа бесконечно малых последовательностей есть

Слайд 13Свойства пределов.

Слайд 14Предел функции
Число b есть предел функции f(x) при x→a если, какова

Слайд 15
a
b
b-ε
b+ε
a-σ
a+σ
x
f(x)
f(x)

Слайд 16Теоремы о пределах

6) Правило Лопиталя:
Теоремы 2-5 см свойства пределов последовательности

Слайд 17Односторонние пределы.
Левый предел
Правый предел

При a=0
Левый предел
Правый предел

a
a

Слайд 18Найти предел функции при x →1
Левый предел:

Правый предел:

Слайд 19Замечательные пределы
Две бесконечно малые называются эквивалентными, если предел их отношения равен

Слайд 20Замечательные пределы

Слайд 21Эквивалентные функции при x → 0
sin x ~ x
tg x ~

Слайд 22Если предел отношения двух бесконечно малых равен некоторому числу k, отличному

Слайд 23Непрерывная функция
ТЕОРЕМА: Функция не может иметь двух различных пределов в

Слайд 24Функция, непрерывная в каждой точке промежутка называется непрерывной на всём промежутке.
Точки,

Слайд 25Свойства непрерывных функций
ТЕОРЕМА 1 , 2 Сумма (произведение) конечного числа непрерывных

Обратная связь

Что такое ThePresentation.ru?

Пределы презентация

Содержание

Слайд 1Числовые последовательностиПредел числовой последовательности и её сходимость

Слайд 2Бесконечной числовой последовательностью называется числовая функция, определённая на множестве натуральных чисел.

Слайд 3Способы задания последовательности:1) В виде формулы – по номеру n-ого членаan=2n2)

Слайд 4Монотонные последовательностиСтрого убывающаяanan-1Возрастающаяan≥an-15; 4; 3;…5; 5; 4; 4; 3…7; 9;

Слайд 5Знакочередующаяся последовательность

Слайд 6Последовательность an называется ограниченной, если существуют такие точки M и m,

Слайд 7Если существует точка М (m), и не существует точка m (M),

Слайд 8ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ.Число а называют пределом числовой последовательности, если для любого

Слайд 9Последовательность, имеющая предел, называется сходящейся, а не имеющая предел – расходящейся.ТЕОРЕМА:

Слайд 10БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ. Бесконечно малой (бм) величиной называется такая

Слайд 11БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ.Последовательность называется бесконечно большой (бб), если для

Слайд 12Свойства бесконечно малой.Сумма и произведение конечного числа бесконечно малых последовательностей есть

Слайд 13Свойства пределов.

Слайд 14Предел функцииЧисло b есть предел функции f(x) при x→a если, какова

Слайд 15abb-εb+εa-σa+σxf(x)f(x)

Слайд 16Теоремы о пределах6) Правило Лопиталя:Теоремы 2-5 см свойства пределов последовательности

Слайд 17Односторонние пределы.Левый пределПравый пределПри a=0Левый пределПравый пределaa

Слайд 18Найти предел функции при x →1Левый предел:Правый предел:

Слайд 19Замечательные пределыДве бесконечно малые называются эквивалентными, если предел их отношения равен

Слайд 20Замечательные пределы

Слайд 21Эквивалентные функции при x → 0sin x ~ xtg x ~

Слайд 22Если предел отношения двух бесконечно малых равен некоторому числу k, отличному

Слайд 23Непрерывная функцияТЕОРЕМА: Функция не может иметь двух различных пределов в

Слайд 24Функция, непрерывная в каждой точке промежутка называется непрерывной на всём промежутке.Точки,

Слайд 25Свойства непрерывных функцийТЕОРЕМА 1 , 2 Сумма (произведение) конечного числа непрерывных

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1Числовые последовательности
Предел числовой последовательности и её сходимость

Слайд 3Способы задания последовательности:
1) В виде формулы – по номеру n-ого члена
an=2n
2)

Слайд 4Монотонные последовательности

Строго убывающая
anan-1

Возрастающая
an≥an-1
5; 4; 3;…
5; 5; 4; 4; 3…
7; 9;

Слайд 8ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ.
Число а называют пределом числовой последовательности, если для любого

Слайд 9Последовательность, имеющая предел, называется сходящейся, а не имеющая предел – расходящейся.
ТЕОРЕМА:

Слайд 10БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ.
Бесконечно малой (бм) величиной называется такая

Слайд 11БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ.
Последовательность называется бесконечно большой (бб), если для

Слайд 12Свойства бесконечно малой.
Сумма и произведение конечного числа бесконечно малых последовательностей есть

Слайд 14Предел функции
Число b есть предел функции f(x) при x→a если, какова

Слайд 15
a
b
b-ε
b+ε
a-σ
a+σ
x
f(x)
f(x)

Слайд 16Теоремы о пределах

6) Правило Лопиталя:
Теоремы 2-5 см свойства пределов последовательности

Слайд 17Односторонние пределы.
Левый предел
Правый предел

При a=0
Левый предел
Правый предел

a
a

Слайд 18Найти предел функции при x →1
Левый предел:

Правый предел:

Слайд 19Замечательные пределы
Две бесконечно малые называются эквивалентными, если предел их отношения равен

Слайд 21Эквивалентные функции при x → 0
sin x ~ x
tg x ~

Слайд 23Непрерывная функция
ТЕОРЕМА: Функция не может иметь двух различных пределов в

Слайд 24Функция, непрерывная в каждой точке промежутка называется непрерывной на всём промежутке.
Точки,

Слайд 25Свойства непрерывных функций
ТЕОРЕМА 1 , 2 Сумма (произведение) конечного числа непрерывных