- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нахождение оптимального сочетания пар объектов по заданным параметрам презентация
Содержание
- 1. Нахождение оптимального сочетания пар объектов по заданным параметрам
- 2. АКТУАЛЬНОСТЬ Существует проблема
- 3. ПРИМЕНЕНИЕ ТЕОРИИ ГРАФОВ Теория графов
- 4. ПОСТАНОВКА ЗАДАЧИ Студентам в группе раздали темы
- 5. Паросочетанием в графе называется такое
- 6. АЛГОРИТМ КУНА Левую долю будем называть студентами,
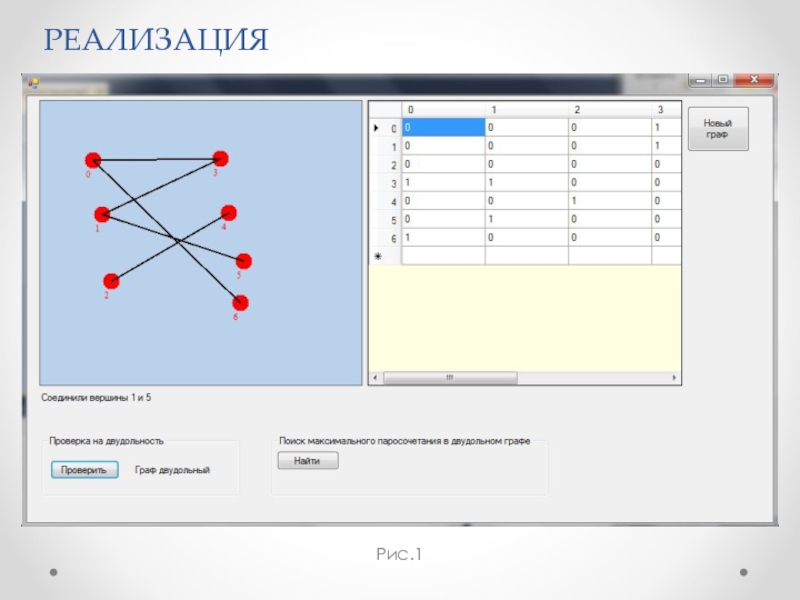
- 7. РЕАЛИЗАЦИЯ Рис.1
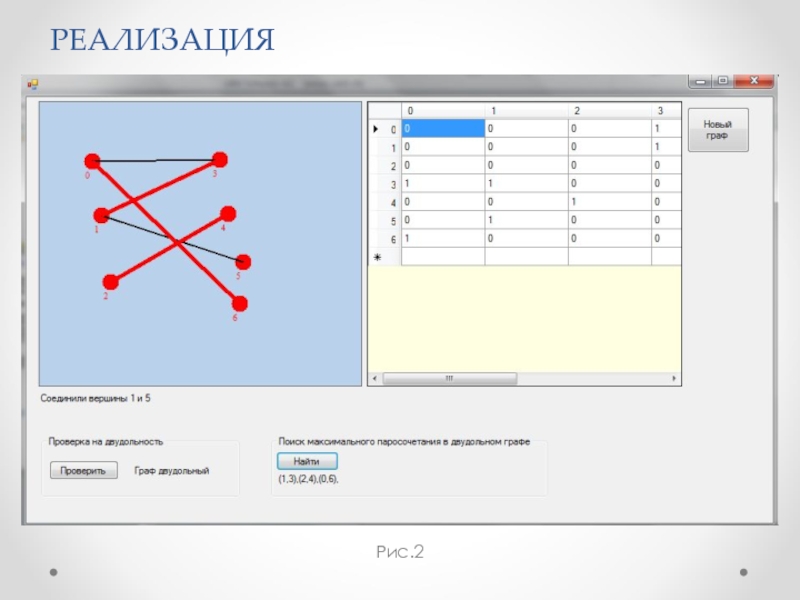
- 8. РЕАЛИЗАЦИЯ Рис.2
- 9. РЕЗУЛЬТАТЫ РАБОТЫ Создана программа на языке программирования
- 10. СПАСИБО ЗА ВНИМАНИЕ
Слайд 1НАХОЖДЕНИЕ ОПТИМАЛЬНОГО СОЧЕТАНИЯ ПАР ОБЪЕКТОВ ПО ЗАДАННЫМ ПАРАМЕТРАМ
Уфа–2013
УГАТУ, ФИРТ
Студентка 3 курса:.
Руководитель: к.т.н. Верхотурова Г.Н.
Слайд 2АКТУАЛЬНОСТЬ
Существует проблема нахождения оптимального сочетания пар объектов по заданным
параметрам
Например, подбор игроков в команду, по определенным качествам или выбор в соответствии с позицией рейтинга наиболее привлекательного задания (темы дипломных проектов в группе, задания на курсовую работу)
Эти задачи могут быть решены с помощью теории графов, а именно, нахождения максимального паросочетания в двудольном графе
Например, подбор игроков в команду, по определенным качествам или выбор в соответствии с позицией рейтинга наиболее привлекательного задания (темы дипломных проектов в группе, задания на курсовую работу)
Эти задачи могут быть решены с помощью теории графов, а именно, нахождения максимального паросочетания в двудольном графе
Слайд 3ПРИМЕНЕНИЕ ТЕОРИИ ГРАФОВ
Теория графов находит применение, например, в геоинформационных системах (ГИС)
Существующие или вновь проектируемые дома, сооружения, кварталы и т.п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередач и т.п. - как рёбра графа
Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут
Слайд 4ПОСТАНОВКА ЗАДАЧИ
Студентам в группе раздали темы на курсовую работу. Чем выше
рейтинг студента, тем наиболее интересную тему он может выбрать (студенты – левая доля графа, курсовые работы – правая доля графа)
Найти оптимальное (все студенты взяли курсовую работу) сочетание пар объектов по заданным параметрам
Создать программу, реализующую нахождение максимального паросочетания в двудольном графе
Найти оптимальное (все студенты взяли курсовую работу) сочетание пар объектов по заданным параметрам
Создать программу, реализующую нахождение максимального паросочетания в двудольном графе
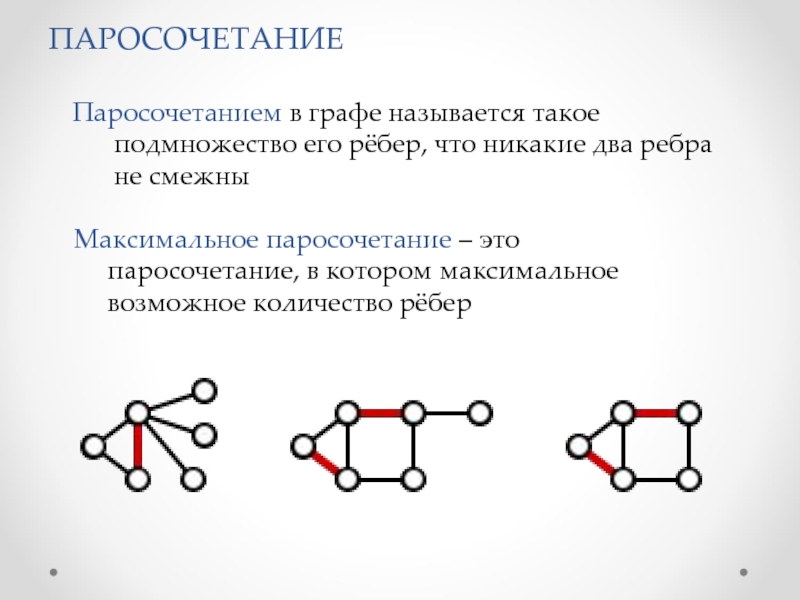
Слайд 5 Паросочетанием в графе называется такое
подмножество его
рёбер, что никакие два ребра
не смежны
Максимальное паросочетание – это
паросочетание, в котором максимальное
возможное количество рёбер
не смежны
Максимальное паросочетание – это
паросочетание, в котором максимальное
возможное количество рёбер
ПАРОСОЧЕТАНИЕ
Слайд 6АЛГОРИТМ КУНА
Левую долю будем называть студентами, а правую курсовыми работами.
Выбираем непересекающиеся
рёбра произвольным образом, пока есть такая возможность.
Построим граф, в котором от студентов ведёт только одно ребро – к курсовой, которую они выбрали. Назовём эти рёбра красными. Остальные рёбра оставим прежними.
Ищем путь в графе от студента, который не выбрал курсовую, к свободным темам, такой, что красные и не красные рёбра в этом пути чередуются. Если такой путь найти не удаётся, завершаем алгоритм.
Поменяем все красные рёбра в найденном пути на не красные, а не красные – на красные.
Если ещё остались студенты и темы, возвращаемся к п.3
Построим граф, в котором от студентов ведёт только одно ребро – к курсовой, которую они выбрали. Назовём эти рёбра красными. Остальные рёбра оставим прежними.
Ищем путь в графе от студента, который не выбрал курсовую, к свободным темам, такой, что красные и не красные рёбра в этом пути чередуются. Если такой путь найти не удаётся, завершаем алгоритм.
Поменяем все красные рёбра в найденном пути на не красные, а не красные – на красные.
Если ещё остались студенты и темы, возвращаемся к п.3
Слайд 9РЕЗУЛЬТАТЫ РАБОТЫ
Создана программа на языке программирования С++, реализующая построение двудольного графа
и находящая максимальное паросочетание в нем по заданному признаку
Найдено оптимальное (все студенты взяли курсовую работу) сочетание пар объектов по заданным параметрам
Найдено оптимальное (все студенты взяли курсовую работу) сочетание пар объектов по заданным параметрам