ДВИЖЕНИЕ
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движение. Преобразование одной фигуры в другую презентация
Содержание
- 1. Движение. Преобразование одной фигуры в другую
- 2. Преобразование одной фигуры в другую называется движением,
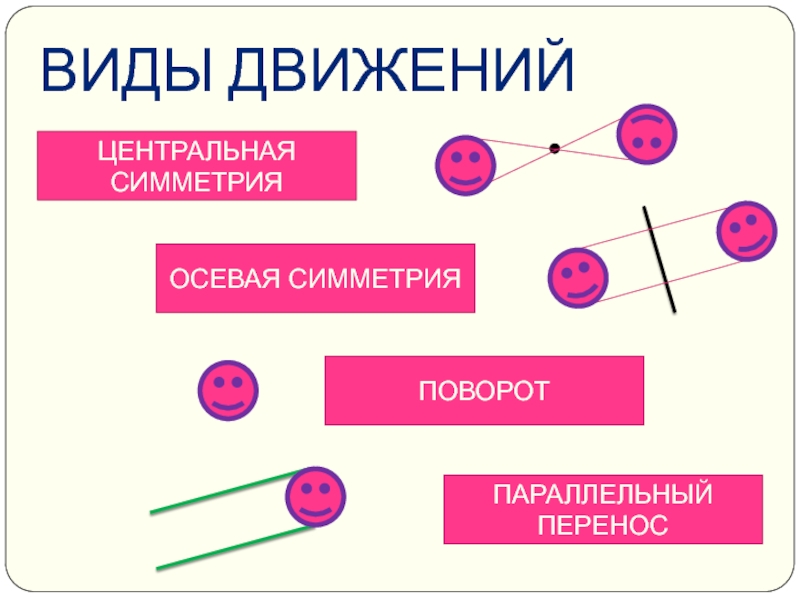
- 3. ВИДЫ ДВИЖЕНИЙ ОСЕВАЯ СИММЕТРИЯ ЦЕНТРАЛЬНАЯ СИММЕТРИЯ ПОВОРОТ
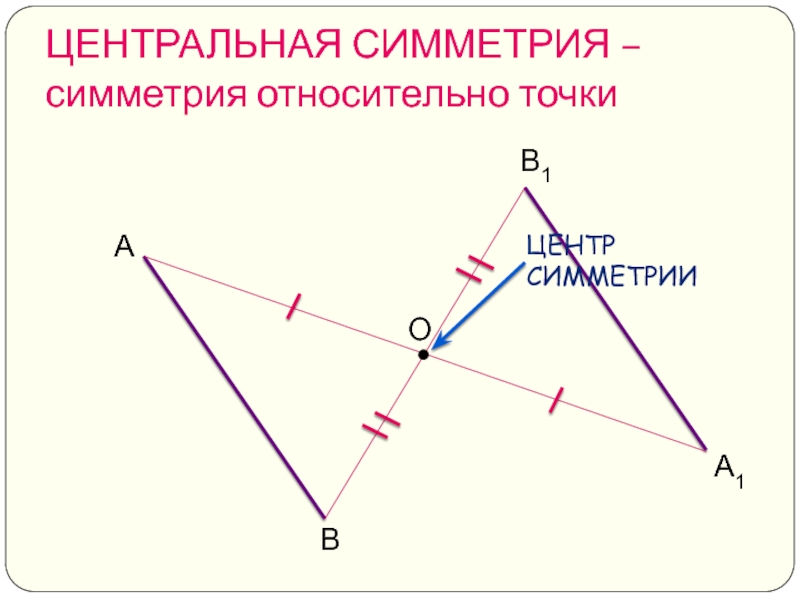
- 4. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ – симметрия относительно точки А1 А В В1 О
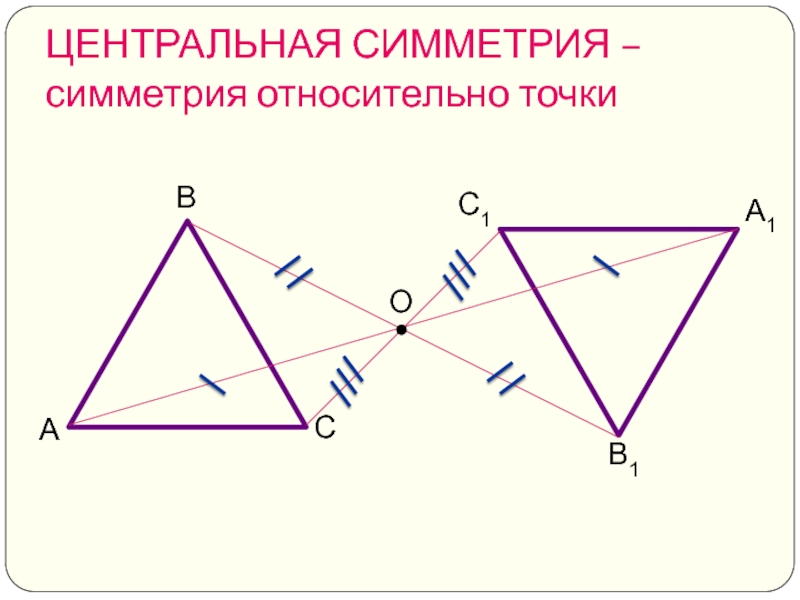
- 5. О А1 В1 С1 ЦЕНТРАЛЬНАЯ СИММЕТРИЯ – симметрия относительно точки
- 6. чтобы построить фигуру, симметричную данной
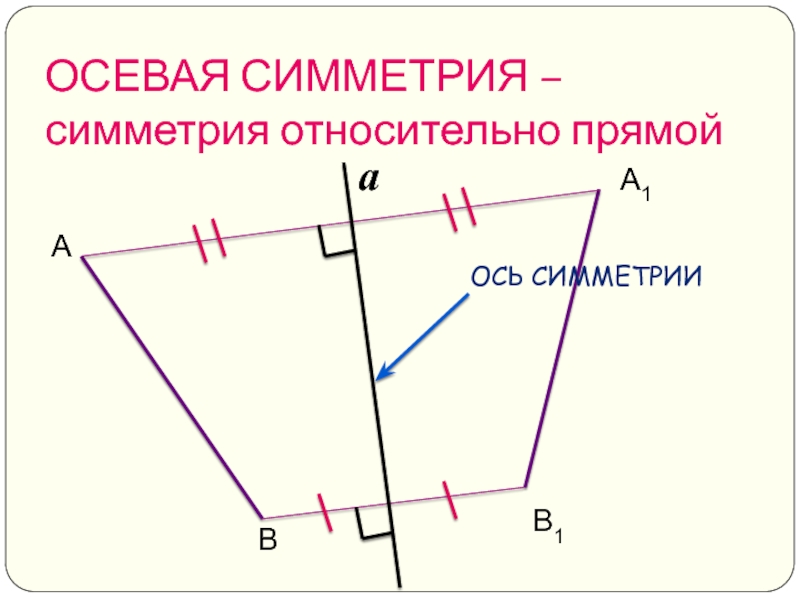
- 7. ОСЕВАЯ СИММЕТРИЯ – симметрия относительно прямой А В А1 В1 a
- 8. ОСЕВАЯ СИММЕТРИЯ – симметрия относительно прямой С1 А1 В1 a
- 9. чтобы построить фигуру, симметричную данной
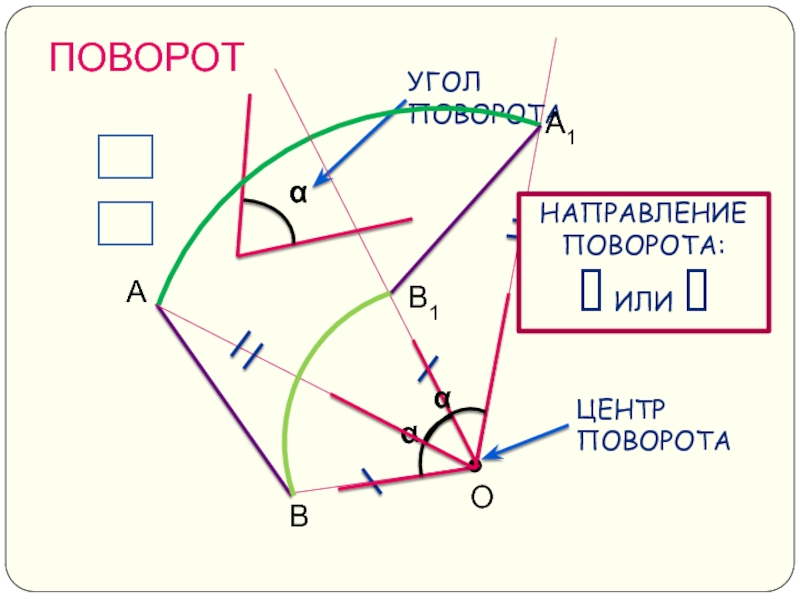
- 10. ПОВОРОТ О А В А1 В1 НАПРАВЛЕНИЕ ПОВОРОТА: ? ИЛИ ⮷ ?
- 11. ПОВОРОТ О А1 В1 С1 ?
- 12. ПОВОРОТ Сделаем вывод: Чтобы получить отображение фигуры
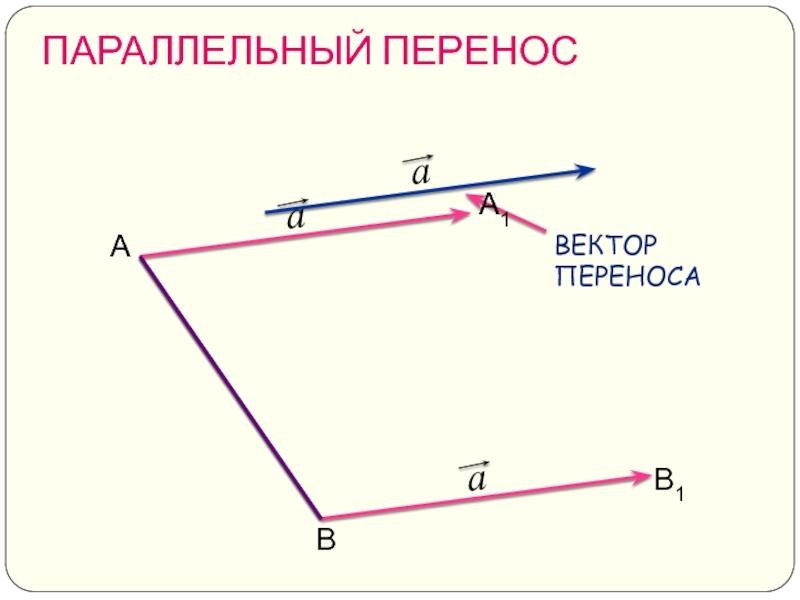
- 13. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС А В А1 В1
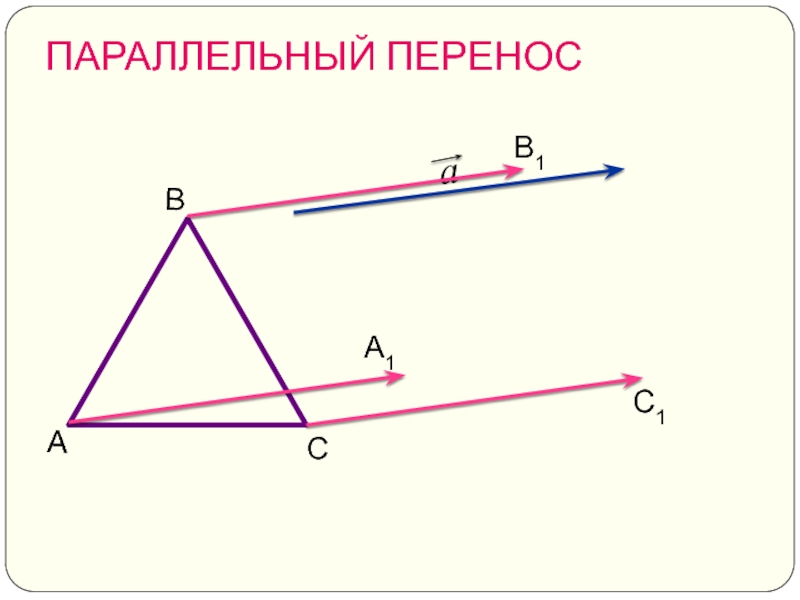
- 14. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС С1 А1 В1 С А В
- 15. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС Сделаем вывод: Чтобы отобразить фигуру
- 16. СВОЙСТВА ДВИЖЕНИЯ Попробуйте сформулировать При движении прямые
- 17. Любая фигура переходит в равную ей фигуру
- 18. ЗАДАЧИ 1. Постройте окружность, симметричную данной относительно
- 19. ПОСТРОЕНИЕ О a 1 О1 R 2 R 3
- 20. ЗАДАЧИ 2. Постройте прямую, симметричную данной относительно
- 21. ПОСТРОЕНИЕ О a 1 А
- 22. ЗАДАЧИ 3. Постройте параллелограмм, полученный с помощью
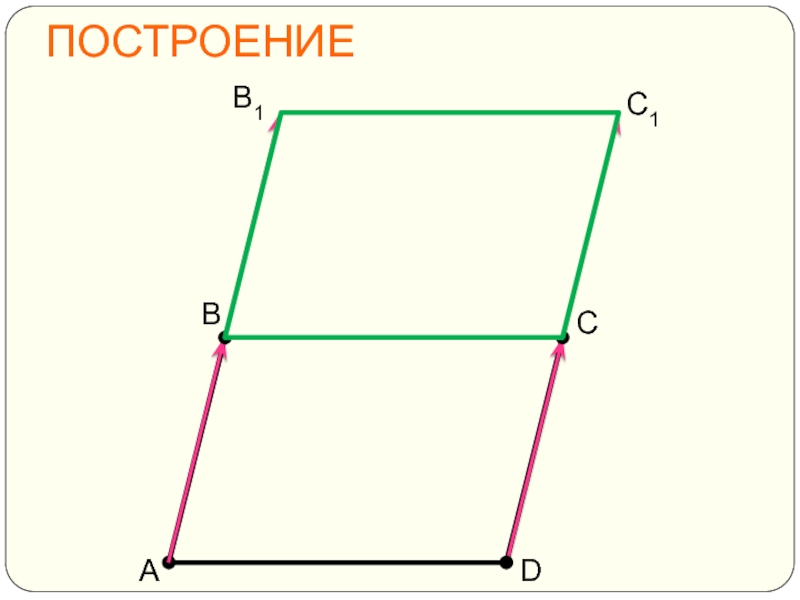
- 23. ПОСТРОЕНИЕ D А С В1 В С1
- 24. ЗАДАЧИ
- 25. Решение: При повороте каждый катет прямоугольного
- 26. ДОМАШНЕЕ ЗАДАНИЕ Определите, при каких видах движения
Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние между точками. Y1 XY = X1Y1
Слайд 1Разработала
учитель математики и информатики МОУ Нахабинская СОШ №3 с УИОП Репкина
Е.А.
Слайд 2Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние
между точками.
Y1
XY = X1Y1
Слайд 6 чтобы построить фигуру, симметричную данной относительно точки О, нужно каждую точку
фигуры соединить с точкой О, продолжить полученный отрезок равным ему, отметить на конце этого отрезка образ исходной точки, затем соединить полученные образы
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ – симметрия относительно точки
Сделаем вывод:
СВОЙСТВА ДВИЖЕНИЯ
Слайд 9 чтобы построить фигуру, симметричную данной относительно прямой а, нужно из каждой
точки фигуры провести перпендикуляр к прямой а, продолжить полученный отрезок равным ему, отметить на конце этого отрезка образ исходной точки, затем соединить полученные образы
ОСЕВАЯ СИММЕТРИЯ –
симметрия относительно прямой
Сделаем вывод:
СВОЙСТВА ДВИЖЕНИЯ
Слайд 12ПОВОРОТ
Сделаем вывод:
Чтобы получить отображение фигуры при повороте около данной точки, нужно
каждую точку фигуры повернуть на один и тот же угол в одном и том же направлении (по часовой стрелке или против часовой стрелки)
СВОЙСТВА ДВИЖЕНИЯ
Слайд 15ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
Сделаем вывод:
Чтобы отобразить фигуру с помощью параллельного переноса, нужно каждую
точку фигуры переместить на заданный вектор, а затем соединить полученные образы
СВОЙСТВА ДВИЖЕНИЯ
Слайд 16СВОЙСТВА ДВИЖЕНИЯ
Попробуйте сформулировать
При движении прямые переходят в прямые, полупрямые – в
полупрямые, отрезки – в отрезки.
Точки, лежащие на прямой, переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
Сохраняются углы между полупрямыми. ЗНАЧИТ…
Точки, лежащие на прямой, переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
Сохраняются углы между полупрямыми. ЗНАЧИТ…
Слайд 18ЗАДАЧИ
1. Постройте окружность, симметричную данной относительно заданной прямой.
Решение:
для построения любой
окружности нужно знать её центр и радиус.
Поэтому, для построения окружности, симметричной данной, нужно :
построить точку, симметричную центру;
измерить радиус исходной окружности;
этим же радиусом построить окружность с центром в симметричной точке.
Поэтому, для построения окружности, симметричной данной, нужно :
построить точку, симметричную центру;
измерить радиус исходной окружности;
этим же радиусом построить окружность с центром в симметричной точке.
ПОСТРОЕНИЕ
Слайд 20ЗАДАЧИ
2. Постройте прямую, симметричную данной относительно заданной точки.
Решение:
Мы знаем, что
через две точки можно провести прямую и притом только одну.
Поэтому, для построения прямой, симметричной данной, нужно :
произвольно выбрать две точки на данной прямой;
построить симметричные им точки;
через полученные точки провести прямую – это и будет искомая прямая.
Поэтому, для построения прямой, симметричной данной, нужно :
произвольно выбрать две точки на данной прямой;
построить симметричные им точки;
через полученные точки провести прямую – это и будет искомая прямая.
ПОСТРОЕНИЕ
Слайд 22ЗАДАЧИ 3. Постройте параллелограмм, полученный с помощью параллельного переноса параллелограмма ABCD на
вектор АВ.
Решение:
Вектор АВ пройдёт вдоль стороны АВ параллелограмма, значит
точка А перейдёт в точку В,
точка В переместится в этом же направлении на длину отрезка АВ в точку В1,
точка С перейдёт таким же образом в точку С1,
точка D перейдёт в точку С.
Таким образом, параллелограмм ABCD перейдёт в параллелограмм ВВ1С1С.
ПОСТРОЕНИЕ
→
→
Слайд 24
ЗАДАЧИ
3. Найдите площадь фигуры, которую опишут катеты прямоугольного треугольника при повороте
на 90° относительно вершины прямого угла.
b
a
b
c
РЕШЕНИЕ
О
Слайд 25Решение:
При повороте каждый катет прямоугольного треугольника описал круговой сектор с
дугой 90°, а точнее – четверть круга.
Радиусом одного сектора является катет а, радиусом второго сектора – катет b.
Следовательно, площади этих секторов будут вычисляться по формулам:
и
Соответственно, для всей фигуры:
или
Радиусом одного сектора является катет а, радиусом второго сектора – катет b.
Следовательно, площади этих секторов будут вычисляться по формулам:
и
Соответственно, для всей фигуры:
или
Слайд 26ДОМАШНЕЕ ЗАДАНИЕ
Определите, при каких видах движения переходят сами в себя следующие
фигуры:
квадрат,
прямоугольник,
ромб,
параллелограмм,
равнобокая трапеция,
равносторонний треугольник,
круг.
Для симметрии укажите центр или ось симметрии,
для поворота – центр, угол и направление поворота,
для параллельного переноса – вектор переноса.
