- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамическое программирование. (Семинар 3) презентация
Содержание
- 1. Динамическое программирование. (Семинар 3)
- 2. Задача динамического программирования Рассмотрим динамическую систему, которая
- 3. Переход системы из состояния
- 4. Задача состоит в том, чтобы найти набор
- 5. Последовательно оптимизируем По формулам, называемым уравнениями Беллмана
- 6. находим максимальное решение задачи.
- 7. Задача о распределении средств между предприятиями Процесс
- 8. Планируется работа двух отраслей промышленности на n
- 9. В конце каждого года возвращённые средства полностью
- 10. Решение: Динамической системой являются два предприятия, состояния
- 11. Далее будем считать, что управление на i-м
- 12. Решение задачи начинается с оптимизации функции
- 13. Далее,
- 16. Планируется работа двух отраслей промышленности на n
- 17. В конце каждого года возвращённые средства полностью
- 18. Решение: Динамической системой являются два предприятия, состояния
- 19. Далее будем считать, что управление на i-м
- 20. Решение задачи начинается с оптимизации функции
- 21. Далее,
- 24. Рассмотрим теперь задачи о распределении средств между несколькими предприятиями на один год.
- 25. Планируется работа n предприятий на один год.
- 26. Задача 3 Определить оптимальный план распределения средств
- 27. Решение: Шагом задачи будем считать выделение средств
- 28. Состояние sk определяется количеством оставшихся после k
- 29. 1 этап. Условная оптимизация 1-й шаг:
- 30. 1 этап. Условная оптимизация 2-й шаг:
- 31. 1 этап. Условная оптимизация 3-й шаг:
- 32. 2 этап. Безусловная оптимизация 1-й шаг:
- 33. 2 этап. Безусловная оптимизация По данным
- 34. 2 этап. Безусловная оптимизация По данным
- 35. Планируется работа n предприятий на один год.
- 36. Задача 4 Определить оптимальный план распределения средств
- 37. Решение: Шагом задачи будем считать выделение средств
- 38. Состояние sk определяется количеством оставшихся после k
- 39. 1 этап. Условная оптимизация 1-й шаг:
- 40. 1 этап. Условная оптимизация 2-й шаг:
- 41. 1 этап. Условная оптимизация 3-й шаг:
- 42. 2 этап. Безусловная оптимизация 1-й шаг:
- 43. 2 этап. Безусловная оптимизация По данным
- 44. 2 этап. Безусловная оптимизация По данным
- 45. Методы оптимизации Функция спроса D(p) определяет спрос
- 46. Методы оптимизации Говорят, что рынок находится в
- 47. Предположим, что на продукцию компании вводится (дополнительный)
- 48. Пусть доход от продажи (выручка):
- 49. Решение: Найдем объем производства без учета дополнительного
- 50. По причине введения дополнительного налога доход производителя
- 51. В результате компания исходит из того, чтобы
- 52. Вычислим максимум функции Т = T(t). Из
- 53. Объем производства: Таким образом, введение дополнительного
- 54. Пусть доход от продажи (выручка):
- 55. Решение: Найдем объем производства без учета дополнительного
- 56. По причине введения дополнительного налога доход производителя
- 57. В результате компания исходит из того, чтобы
- 58. Вычислим максимум функции Т = T(t). Из
- 59. Объем производства: Таким образом, введение дополнительного
- 60. Для товаров X1 и X2 известны
- 61. Решение: Найдем цены товаров X1 и X2
- 62. Критические точки функции
- 63. имеет угловые миноры Поэтому
- 64. Для товаров X1 и X2 известны
- 65. Решение: Найдем цены товаров X1 и X2
- 66. Критические точки функции
- 67. имеет угловые миноры
- 68. Ответ:
- 69. Задачи многокритериальной оптимизации Задача вида:
- 70. Пусть X и Y – два допустимых
- 71. Множество эффективных (недоминируемых) решений называется множеством Парето.
- 72. Алгоритм построения Парето-эффективной границы: 1. Строим допустимое
- 73. Каждая из этих линий разбивает плоскость XOY
- 74. Найти Парето-эффективную границу задачи:
- 75. Решение: По условию задачи область допустимых решений
- 76. В качестве допустимого множества получаем
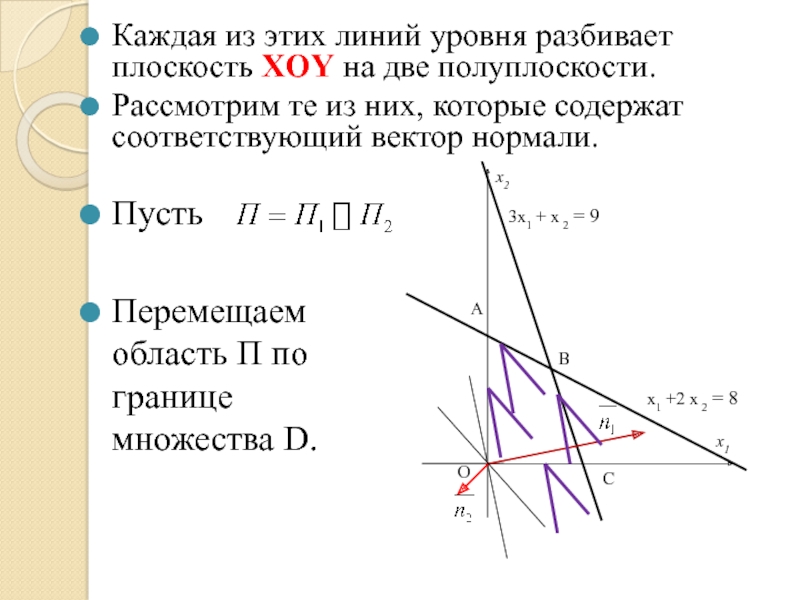
- 77. Каждая из этих линий уровня
- 78. x2 x2 = 4 x1
- 79. Найти Парето-эффективную границу задачи:
- 80. Решение: По условию задачи область допустимых решений
- 81. В качестве допустимого множества
- 82. x2 x1 +2 x
- 83. x2 x1 +2 x
- 84. Метод идеальной точки Метод идеальной точки является геометрическим методом для многокритериальных задач.
- 85. Решить задачу многокритериальной оптимизации методом идеальной
- 86. Решение: По условию задачи область допустимых решений
- 87. В качестве допустимого множества получаем область ОАВСDЕ
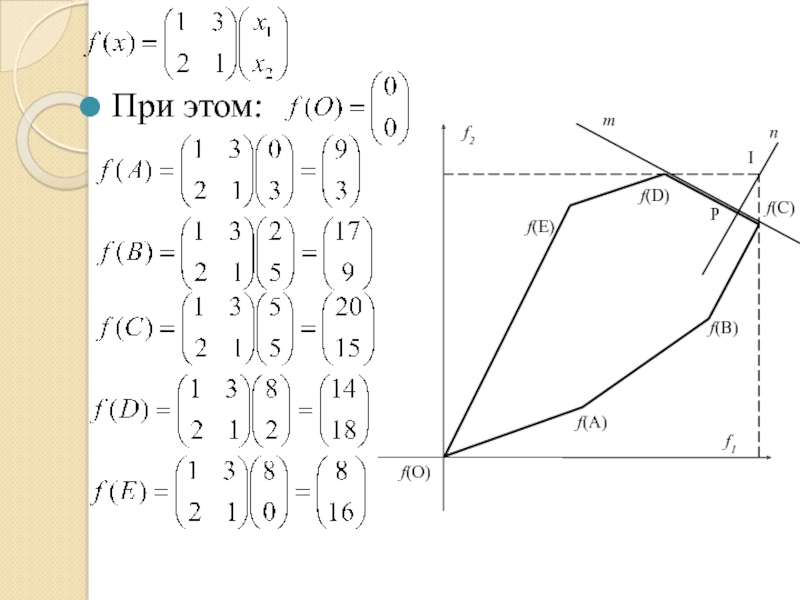
- 88. При этом:
- 89. f2 f(E) f(D) I m n P
- 90. f2 f(E) f(D) I m n P
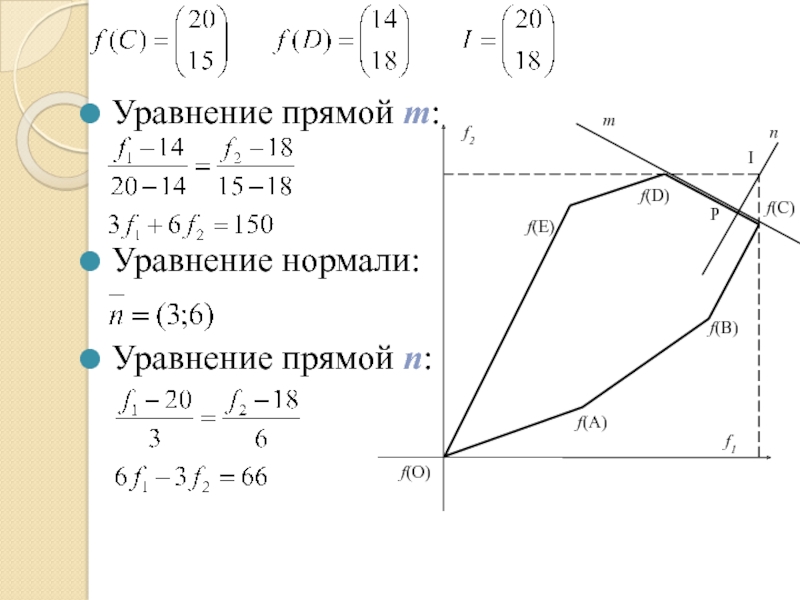
- 91. Уравнение прямой m: Уравнение нормали:
- 92. Решим систему уравнений:
- 93. Решить задачу многокритериальной оптимизации методом идеальной
- 94. Решение: По условию задачи область допустимых решений
- 95. В качестве допустимого множества получаем область ОАВСD
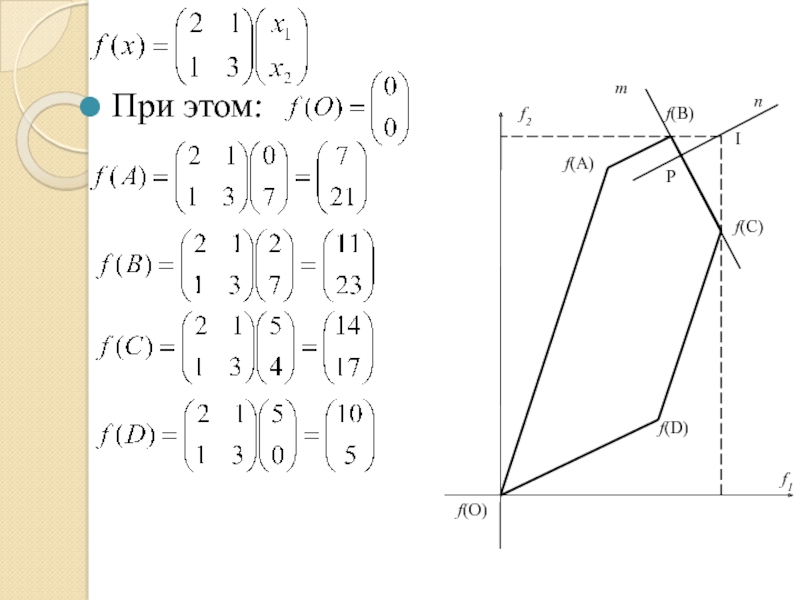
- 96. При этом:
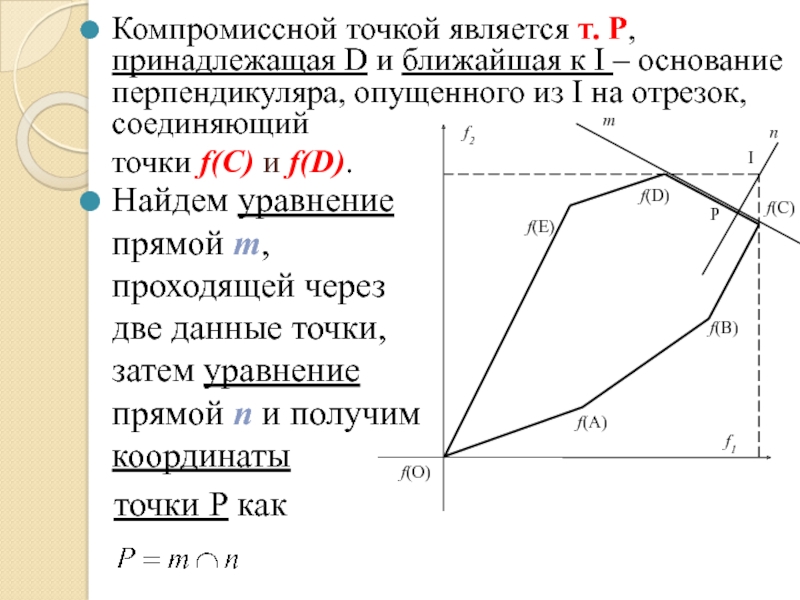
- 97. f2 f(D) I m n P По
- 98. f2 f(D) I m n P Компромиссной
- 99. f2 f(D) I m n P Уравнение
- 100. Решим систему уравнений:
- 101. Спасибо за внимание!
Слайд 2Задача динамического программирования
Рассмотрим динамическую систему, которая последовательно за n шагов переходит
Промежуточные состояния определяют состояния системы после i-го шага. Как правило, состояния системы определяются несколькими числами, поэтому предполагается, что являются векторами, т.е.
Слайд 3Переход системы из состояния в состояние
Эффективность каждого шага оценивается функциями .
Таким образом, эффективность всего процесса характеризуется суммой
Слайд 4Задача состоит в том, чтобы найти набор управлений
Процесс решения разбивается на n шагов.
Введём функцию:
- эта функция характеризует эффективность перехода от состояния к .
Слайд 7Задача о распределении средств между предприятиями
Процесс решения задачи начинается с оптимизации
Рассмотрим теперь несколько задач о распределении средств между предприятиями на несколько лет.
Слайд 8Планируется работа двух отраслей промышленности на n лет. Начальные ресурсы составляют
Аналогично, для второй отрасли прибыль составляет , а возврат
Задача 1
Слайд 9В конце каждого года возвращённые средства полностью распределяются между предприятиями. Определить
n = 4, а
Задача 1
Слайд 10Решение:
Динамической системой являются два предприятия, состояния которых определяются вложенными
Так как возвращённые средства распределяются полностью, то имеет место условие
т.е. и фактически задача одномерна.
Слайд 11Далее будем считать, что управление на i-м году определяется числами
В силу того же условия уравнения состояний имеют вид:
А прибыль на i-м году равна:
Слайд 12Решение задачи начинается с оптимизации функции
Для вычисления максимума заметим, что требуется найти максимум линейной функции на отрезке, поэтому:
при
Слайд 14
Таким образом, поскольку на каждом шаге
,то средства каждый год вкладываются в первую отрасль:
у.е.
у.е.
у.е.
Слайд 15
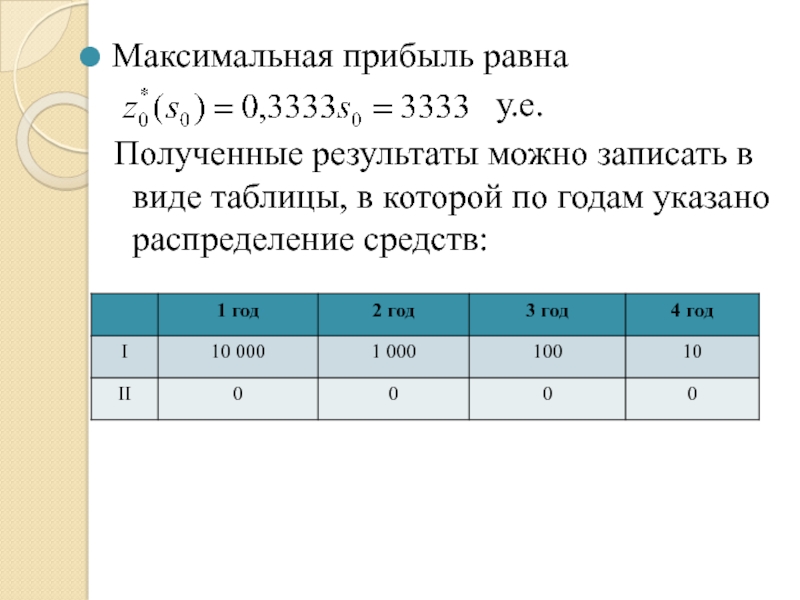
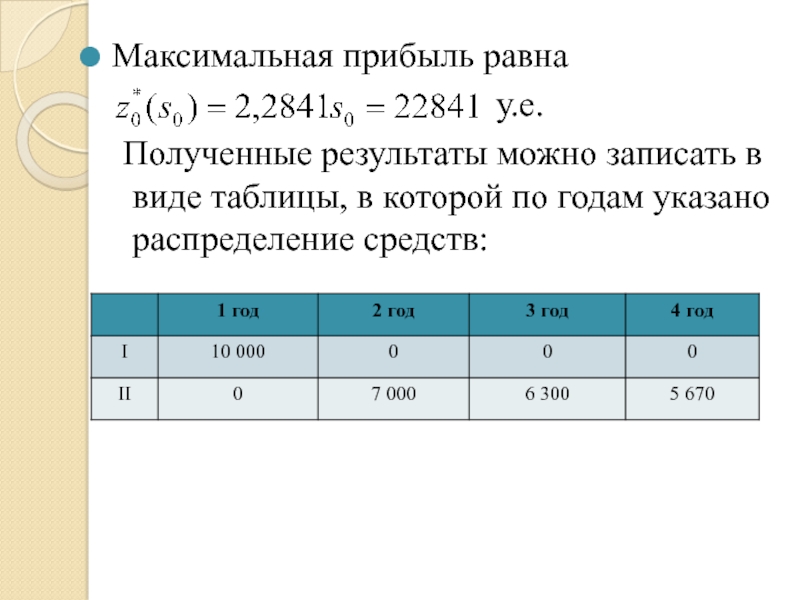
Максимальная прибыль равна
у.е.
Полученные результаты можно записать в виде таблицы, в которой по годам указано распределение средств:
Слайд 16Планируется работа двух отраслей промышленности на n лет. Начальные ресурсы составляют
Аналогично, для второй отрасли прибыль составляет , а возврат
Задача 2
Слайд 17В конце каждого года возвращённые средства полностью распределяются между предприятиями. Определить
n = 4, а
Задача 2
Слайд 18Решение:
Динамической системой являются два предприятия, состояния которых определяются вложенными
Так как возвращённые средства распределяются полностью, то имеет место условие
т.е. и фактически задача одномерна.
Слайд 19Далее будем считать, что управление на i-м году определяется числами
В силу того же условия уравнения состояний имеют вид:
А прибыль на i-м году равна:
Слайд 20Решение задачи начинается с оптимизации функции
Для вычисления максимума заметим, что требуется найти максимум линейной функции на отрезке, поэтому:
при
Слайд 22
Таким образом на первом шаге , т.е. средства в четвёртом периоде вкладываются только в первую отрасль, а на последующих шагах средства вкладываются только во вторую отрасль, т.к.
у.е.
у.е.
у.е.
Слайд 23
Максимальная прибыль равна
у.е.
Полученные результаты можно записать в виде таблицы, в которой по годам указано распределение средств:
Слайд 24Рассмотрим теперь задачи о распределении средств между несколькими предприятиями на один
Слайд 25Планируется работа n предприятий на один год. Начальные средства равны
Задача 3
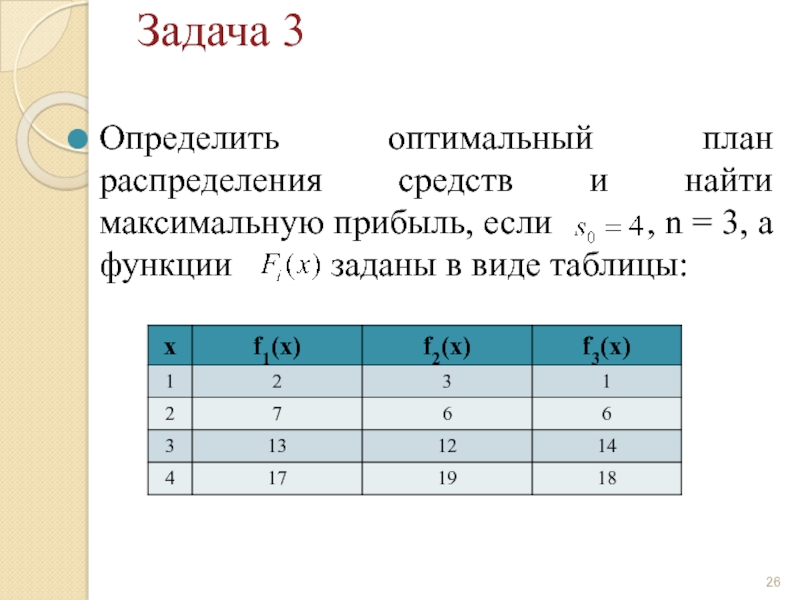
Слайд 26Задача 3
Определить оптимальный план распределения средств и найти максимальную прибыль, если
Слайд 27Решение:
Шагом задачи будем считать выделение средств очередному предприятию, а переменные управления
Таким образом, получаем следующую задачу оптимизации:
Слайд 28Состояние sk определяется количеством оставшихся после k шагов средств (средств, вкладываемых
Уравнения состояний:
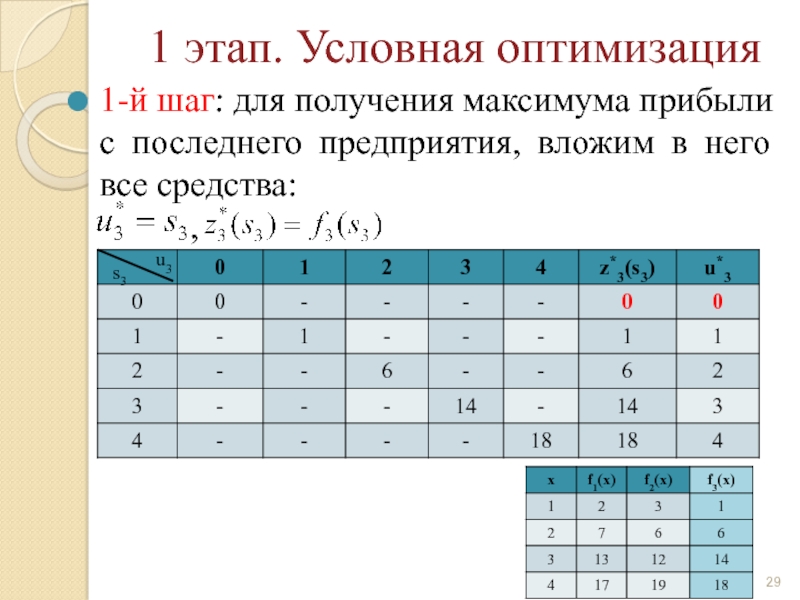
Слайд 29 1 этап. Условная оптимизация
1-й шаг: для получения максимума прибыли с
,
u3
s3
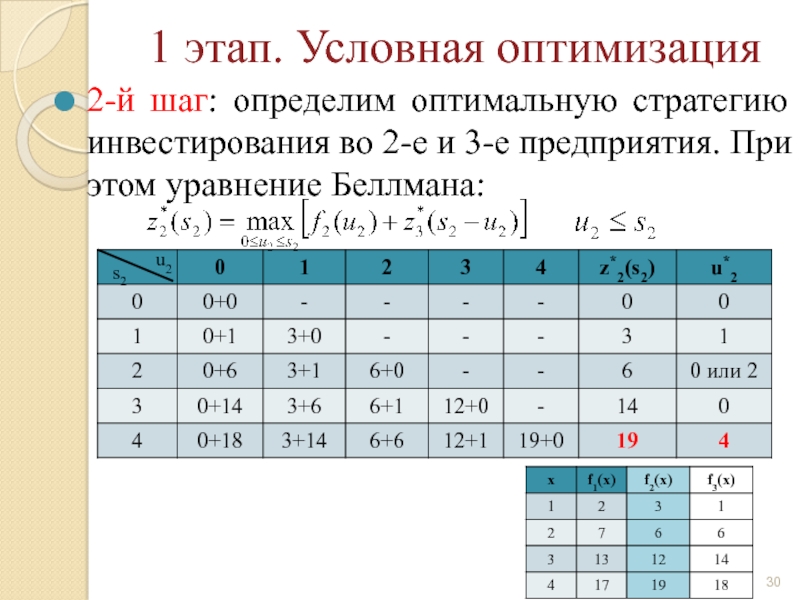
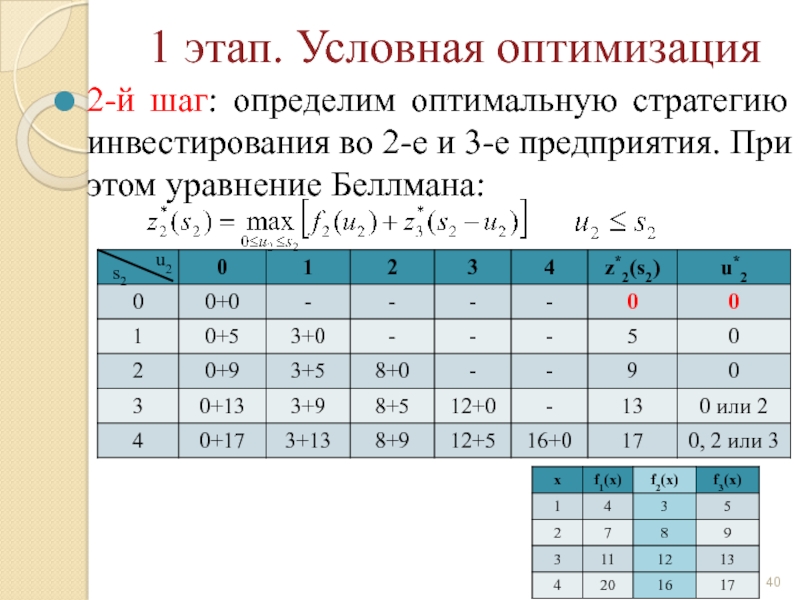
Слайд 30 1 этап. Условная оптимизация
2-й шаг: определим оптимальную стратегию инвестирования во
u2
s2
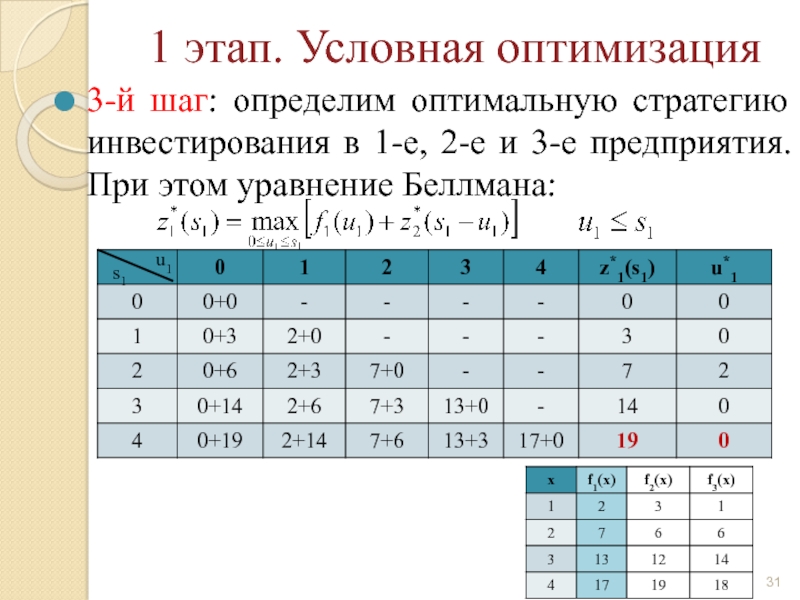
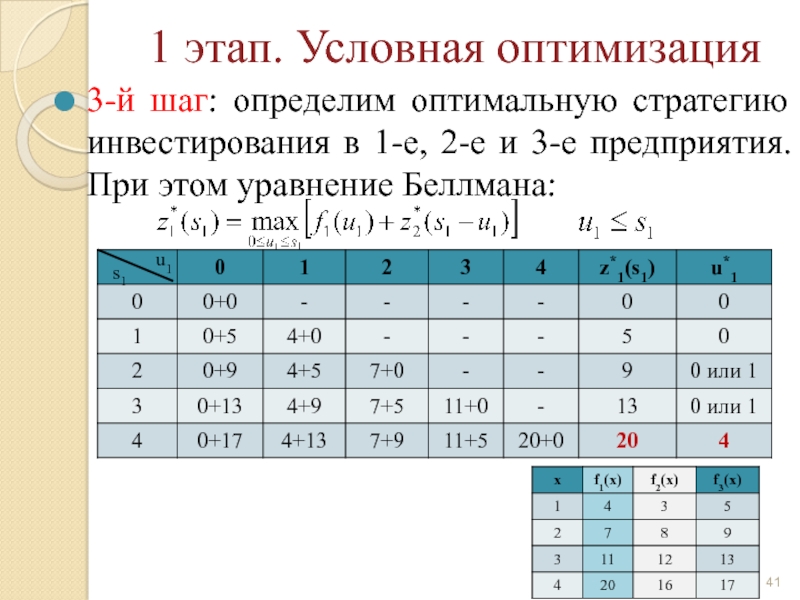
Слайд 31 1 этап. Условная оптимизация
3-й шаг: определим оптимальную стратегию инвестирования в
u1
s1
Слайд 32 2 этап. Безусловная оптимизация
1-й шаг: максимальный доход при инвестировании 4
При этом 1-му предприятию нужно выделить
тыс. у.е.
2-й шаг: Определим величину оставшихся денежных средств, приходящегося на долю
2-го и 3-го предприятий:
тыс. у.е.
Слайд 33 2 этап. Безусловная оптимизация
По данным 2-й таблицы оптимальный вариант распределения
При этом 2-му предприятию нужно выделить
тыс. у.е.
3-й шаг: Определим величину оставшихся денежных средств, приходящегося на долю
3-го предприятия:
тыс. у.е.
Слайд 34 2 этап. Безусловная оптимизация
По данным 1-й таблицы оптимальный вариант распределения
При этом 3-му предприятию нужно выделить
тыс. у.е.
Таким образом, оптимальный план инвестирования предприятий , обеспечивающий максимальный доход, равный:
тыс. у.е.
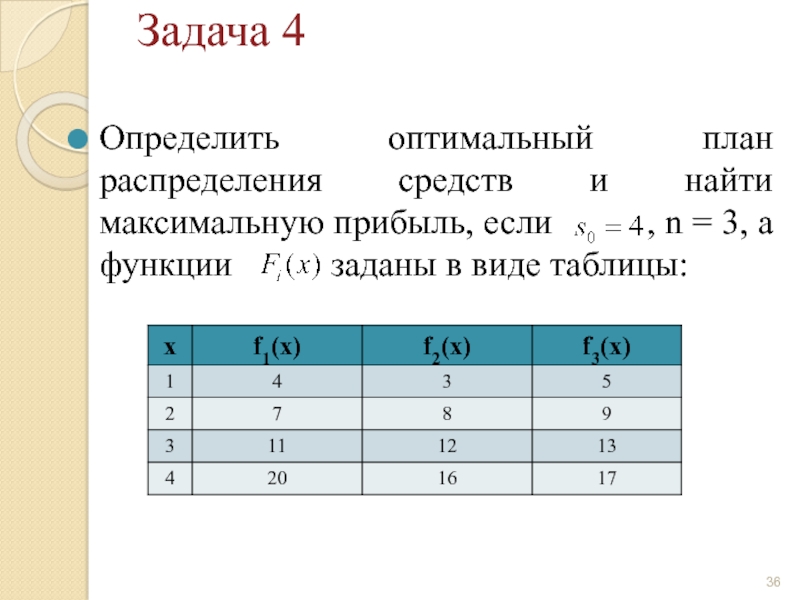
Слайд 35Планируется работа n предприятий на один год. Начальные средства равны
Задача 4
Слайд 36Задача 4
Определить оптимальный план распределения средств и найти максимальную прибыль, если
Слайд 37Решение:
Шагом задачи будем считать выделение средств очередному предприятию, а переменные управления
Таким образом, получаем следующую задачу оптимизации:
Слайд 38Состояние sk определяется количеством оставшихся после k шагов средств (средств, вкладываемых
Уравнения состояний:
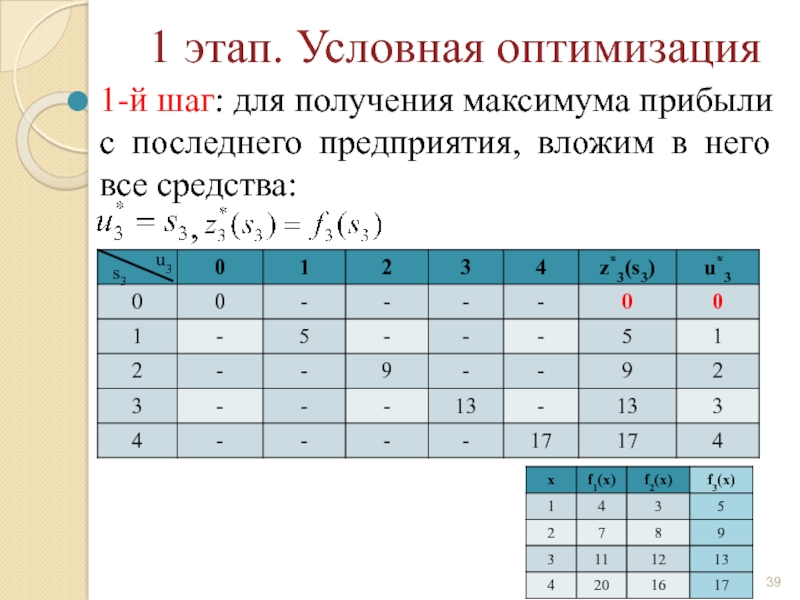
Слайд 39 1 этап. Условная оптимизация
1-й шаг: для получения максимума прибыли с
,
u3
s3
Слайд 40 1 этап. Условная оптимизация
2-й шаг: определим оптимальную стратегию инвестирования во
u2
s2
Слайд 41 1 этап. Условная оптимизация
3-й шаг: определим оптимальную стратегию инвестирования в
u1
s1
Слайд 42 2 этап. Безусловная оптимизация
1-й шаг: максимальный доход при инвестировании 4
При этом 1-му предприятию нужно выделить
тыс. у.е.
2-й шаг: Определим величину оставшихся денежных средств, приходящегося на долю
2-го и 3-го предприятий:
тыс. у.е.
Слайд 43 2 этап. Безусловная оптимизация
По данным 2-й таблицы оптимальный вариант распределения
При этом 2-му предприятию нужно выделить
тыс. у.е.
3-й шаг: Определим величину оставшихся денежных средств, приходящегося на долю
3-го предприятия:
тыс. у.е.
Слайд 44 2 этап. Безусловная оптимизация
По данным 1-й таблицы оптимальный вариант распределения
При этом 3-му предприятию нужно выделить
тыс. у.е.
Таким образом, оптимальный план инвестирования предприятий , обеспечивающий максимальный доход, равный:
тыс. у.е.
Слайд 45Методы оптимизации
Функция спроса D(p) определяет спрос (количество купленного товара) при цене
Функция предложения S(p) задает количество товара, которое поставщик может предложить по рыночной цене p.
Слайд 46Методы оптимизации
Говорят, что рынок находится в равновесии, если покупатели могут купить
Равновесная цена р0 товара на рынке находится из условия S(р0) = D(р0), а количество q0 проданного товара q0 = D(р0).
Слайд 47Предположим, что на продукцию компании вводится (дополнительный) фиксированный налог t на
Если ставка налога достаточно велика, то производство товара будет невыгодно, и это приведет его к остановке.
Возникает вопрос о такой ставке налога, чтобы итоговый сбор был максимальным.
1. Оптимизация налогообложения
Слайд 48 Пусть доход от продажи (выручка):
а затраты на выпуск продукта
Найти величину налога t на каждую единицу продукта, чтобы налог T=tq от всей реализуемой продукции был максимальным, и весь налоговый сбор.
Как уменьшится количество выпускаемой продукции?
Задача 5
Слайд 49Решение:
Найдем объем производства без учета дополнительного налога.
Найдем функцию прибыли:
Из ее
находим, что максимум прибыли достигается при объеме производства:
Слайд 50По причине введения дополнительного налога доход производителя уменьшится на величину Т
а его прибыль
Слайд 51В результате компания исходит из того, чтобы при реализации товара получить
Решим уравнение:
Общая налоговая выплата составит:
Слайд 52Вычислим максимум функции Т = T(t).
Из условия T’(t) = 0 следует,
т.е.
Точка является точкой максимума функции T(t). При этом весь налоговый сбор:
Слайд 53Объем производства:
Таким образом, введение дополнительного налога уменьшает объем производства в 2
Ответ:
Слайд 54 Пусть доход от продажи (выручка):
а затраты на выпуск продукта
Найти величину налога t на каждую единицу продукта, чтобы налог T=tq от всей реализуемой продукции был максимальным, и весь налоговый сбор.
Как уменьшится количество выпускаемой продукции?
Задача 6
Слайд 55Решение:
Найдем объем производства без учета дополнительного налога.
Найдем функцию прибыли:
Из ее
находим, что максимум прибыли достигается при объеме производства:
Слайд 56По причине введения дополнительного налога доход производителя уменьшится на величину Т
а его прибыль
Слайд 57В результате компания исходит из того, чтобы при реализации товара получить
Решим уравнение:
Общая налоговая выплата составит:
Слайд 58Вычислим максимум функции Т = T(t).
Из условия T’(t) = 0 следует,
т.е.
Точка является точкой максимума функции T(t). При этом весь налоговый сбор:
Слайд 59Объем производства:
Таким образом, введение дополнительного налога уменьшает объем производства в 2
Ответ:
Слайд 60 Для товаров X1 и X2 известны функции спроса:
Фирма-монополист имеет функцию издержек:
Вычислите максимальную прибыль фирмы в этих условиях и найдите соответствующий производственный план.
Задача 7
2. Оптимизация прибыли
Слайд 62Критические точки функции найдем из
Решением системы является точка (5;4).
Найдем матрицу вторых производных G(П) функции , которая не зависит от точки:
Слайд 63имеет угловые миноры
Поэтому точка (5;4) в силу выпуклости функции
Ответ:
Слайд 64 Для товаров X1 и X2 известны функции спроса:
Фирма-монополист имеет функцию издержек:
Вычислите максимальную прибыль фирмы в этих условиях и найдите соответствующий производственный план.
Задача 8
Слайд 66Критические точки функции найдем из
Решением системы является точка:
Найдем матрицу вторых производных G(П) функции , которая не зависит от точки:
Слайд 67имеет угловые миноры
Поэтому точка
Слайд 69Задачи многокритериальной оптимизации
Задача вида:
где i > 1,
fi(x) – гладкие функции на D, называется задачей многокритериальной оптимизации.
Область допустимых решений D задается системой уравнений и неравенств.
Слайд 70Пусть X и Y – два допустимых решения. Говорят, что X
i = 1, 2, …, n выполняется неравенство
fi(X) ≥ fi(Y) и найдется такое k, что fk(X) > fk(Y).
Решение Z называется недоминируемым (эффективным), если нет решения X, которое бы доминировало Z.
Слайд 71Множество эффективных (недоминируемых) решений называется множеством Парето.
Геометрическое изображение множества Парето называется
В задаче многокритериальной оптимизации наилучшее решение следует искать в множестве Парето.
Слайд 72Алгоритм построения Парето-эффективной границы:
1. Строим допустимое множество D, заданное системой ограничений
2. Для каждой функции
строим линию уровня как прямую, перпендикулярную соответствующему вектору нормали .
Слайд 73Каждая из этих линий разбивает плоскость XOY на две полуплоскости.
Пусть Пi
3. Перемещая данную область П по границе допустимого множества D, находим те точки границы, которые являются единственными точками пересечения областей П и D.
Данные точки - оптимальные по Парето, а множество всех таких точек – Парето-эффективная граница.
Слайд 75Решение:
По условию задачи область допустимых решений задана системой неравенств:
Построим данную область:
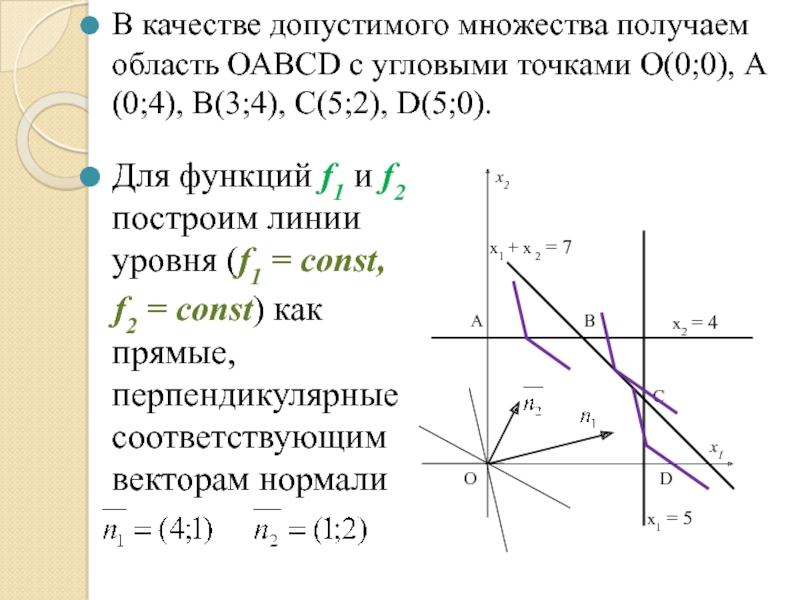
Слайд 76
В качестве допустимого множества получаем область ОАВСD с угловыми точками О(0;0),
x2
x2 = 4
x1 + x 2 = 7
Для функций f1 и f2 построим линии уровня (f1 = const,
f2 = const) как прямые, перпендикулярные соответствующим векторам нормали
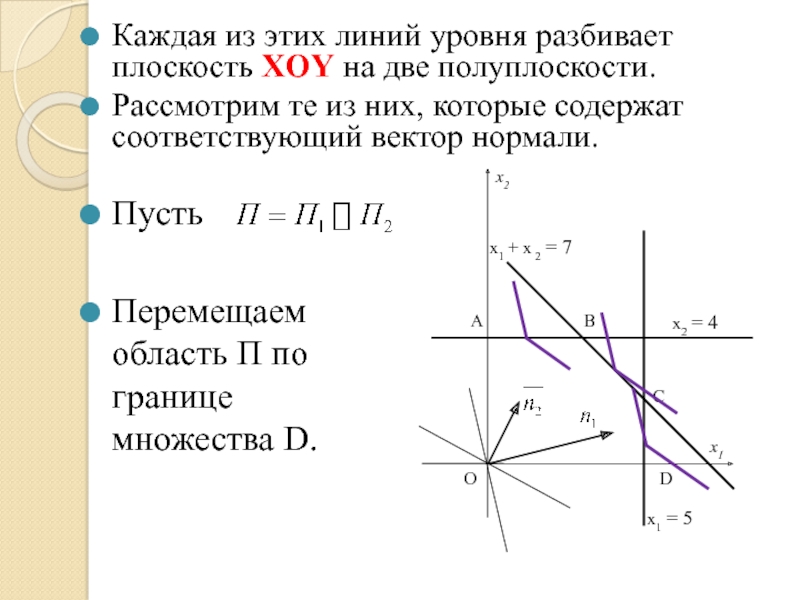
Слайд 77
Каждая из этих линий уровня разбивает плоскость XOY на две полуплоскости.
Рассмотрим те из них, которые содержат соответствующий вектор нормали.
x2
x2 = 4
x1 + x 2 = 7
Пусть
Перемещаем область П по границе множества D.
Слайд 78
x2
x2 = 4
x1 + x 2 = 7
Парето-эффективной границей будет отрезок
Ответ:
[BC] - Парето-эффективная граница; множество точек
Слайд 80Решение:
По условию задачи область допустимых решений задана системой неравенств:
Построим данную область:
Слайд 81
В качестве допустимого множества получаем область ОАВС с угловыми точками О(0;0),
x2
x1 +2 x 2 = 8
Для функций f1 и f2 построим линии уровня (f1 = const,
f2 = const) как прямые, перпендикулярные соответствующим векторам нормали
3x1 + x 2 = 9
Слайд 82
x2
x1 +2 x 2 = 8
3x1 + x 2 = 9
Каждая
Рассмотрим те из них, которые содержат соответствующий вектор нормали.
Пусть
Перемещаем область П по границе множества D.
Слайд 83
x2
x1 +2 x 2 = 8
3x1 + x 2 = 9
Парето-эффективной
Ответ:
[OС] - Парето-эффективная граница; множество точек
Слайд 84Метод идеальной точки
Метод идеальной точки является геометрическим методом для многокритериальных задач.
Слайд 86Решение:
По условию задачи область допустимых решений задана системой неравенств:
Построим данную область:
Слайд 87В качестве допустимого множества получаем область ОАВСDЕ с угловыми точками О(0;0),
x2
x2 = 5
x1 + x 2 = 10
- x1 + x 2 = 3
Е
Введем линейное преобразование f:
, определенное критериями f1 и f2:
Слайд 89f2
f(E)
f(D)
I
m
n
P
По причине линейности f строим образ области D под действием преобразования
шестиугольник с
вершинами f(О), f(А),
f(В), f(С), f(D), f(E).
Идеальная точка – I с координатами (f1.max; f2.max), которая не пренадлежит образу D.
Слайд 90f2
f(E)
f(D)
I
m
n
P
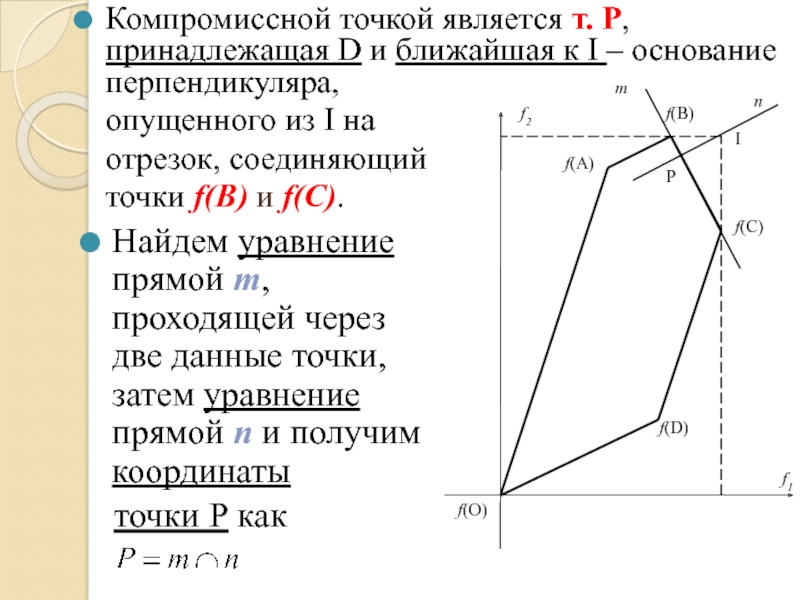
Компромиссной точкой является т. Р, принадлежащая D и ближайшая к I
точки f(С) и f(D).
Найдем уравнение прямой m, проходящей через две данные точки, затем уравнение прямой n и получим координаты
точки Р как
Слайд 94Решение:
По условию задачи область допустимых решений задана системой неравенств:
Построим данную область:
Слайд 95В качестве допустимого множества получаем область ОАВСD с угловыми точками О(0;0),
x2
x1 + x 2 = 9
x 2 = 7
Введем линейное преобразование f:
, определенное критериями f1 и f2:
Слайд 97f2
f(D)
I
m
n
P
По причине линейности f строим образ области D под действием преобразования
пятиугольник с
вершинами f(О), f(А),
f(В), f(С), f(D).
Идеальная точка – I с координатами (f1.max; f2.max), которая не пренадлежит образу D.
Слайд 98f2
f(D)
I
m
n
P
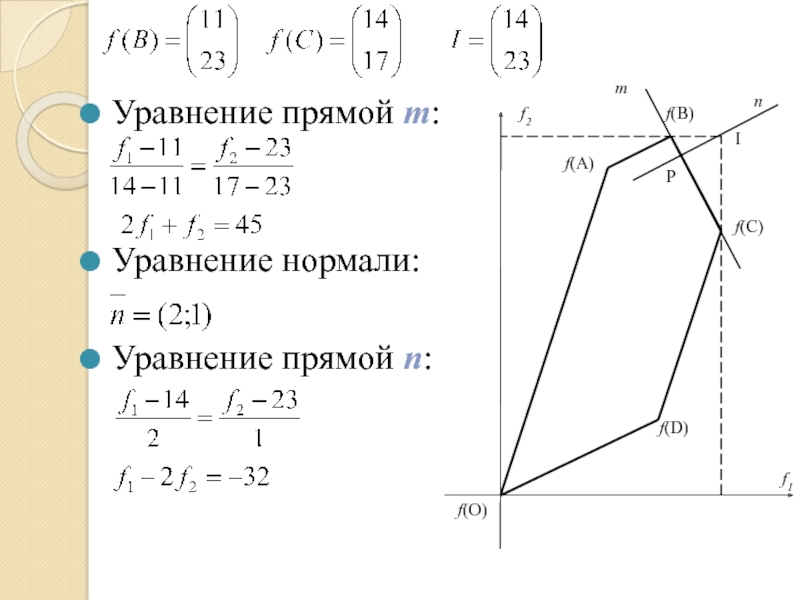
Компромиссной точкой является т. Р, принадлежащая D и ближайшая к I
опущенного из I на
отрезок, соединяющий
точки f(В) и f(С).
Найдем уравнение прямой m, проходящей через две данные точки, затем уравнение прямой n и получим координаты
точки Р как












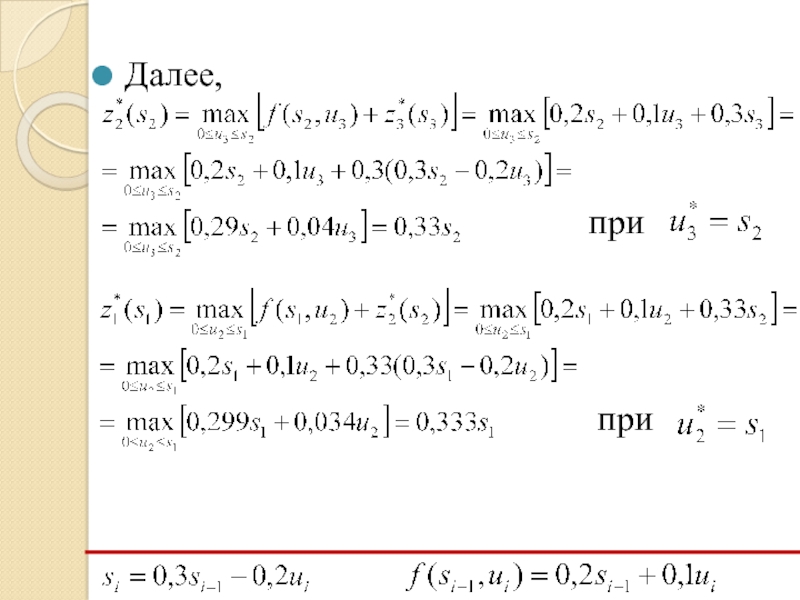






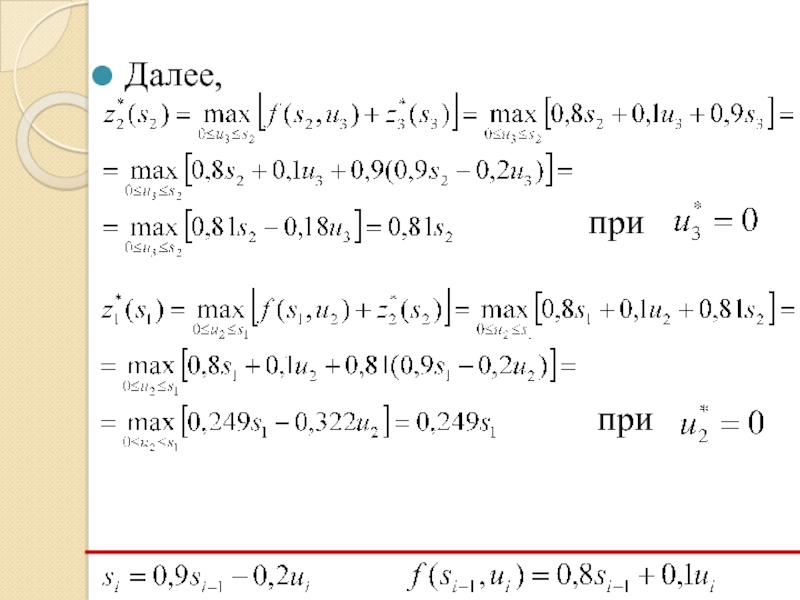













































![x2x2 = 4x1 + x 2 = 7Парето-эффективной границей будет отрезок [BC]: множество точекОтвет: [BC]](/img/tmb/5/414002/51d5bdcef3df873d33f1a867cc946f4d-800x.jpg)



![x2x1 +2 x 2 = 83x1 + x 2 = 9Парето-эффективной границей будет отрезок [OС]:](/img/tmb/5/414002/476228d37c7612758704d2375cec18b3-800x.jpg)