Рунге
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численное интегрирование и его погрешности. Методы прямоугольников и трапеций. Метод Симпсона. Правило Рунге. (Лекция 5) презентация
Содержание
- 1. Численное интегрирование и его погрешности. Методы прямоугольников и трапеций. Метод Симпсона. Правило Рунге. (Лекция 5)
- 2. Определенный интеграл Из курса математического анализа известно,
- 3. Методы интегрирования
- 5. Приближенное вычисление площади криволинейной трапеции Для приближенного
- 6. Замена подинтегральной функции интерполяционными полиномами В качестве
- 7. Методы численного интегрирования Для получения простых формул
- 8. Методы прямоугольников В методах прямоугольников подинтегральная функция
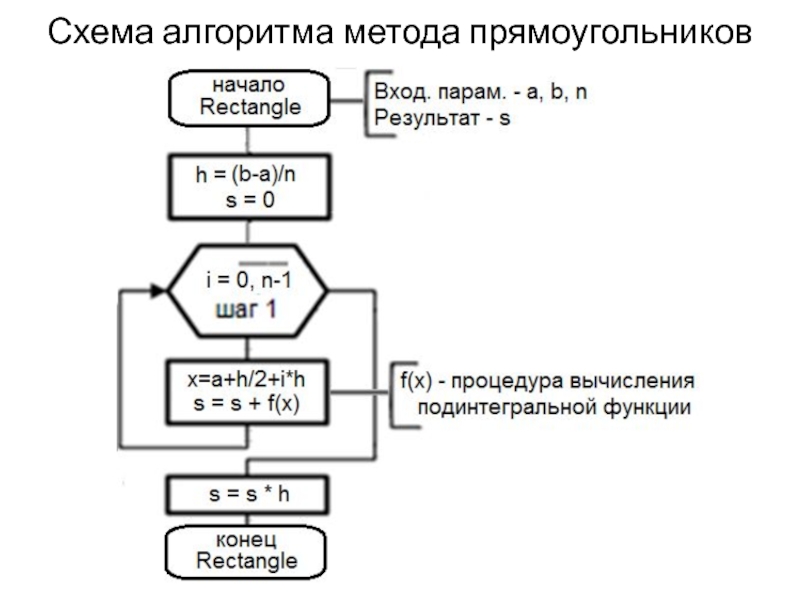
- 12. Схема алгоритма метода прямоугольников
- 13. Метод трапеций В методе трапеций подинтегральная функция
- 14. Метод трапеций
- 15. Вывод формулы трапеций
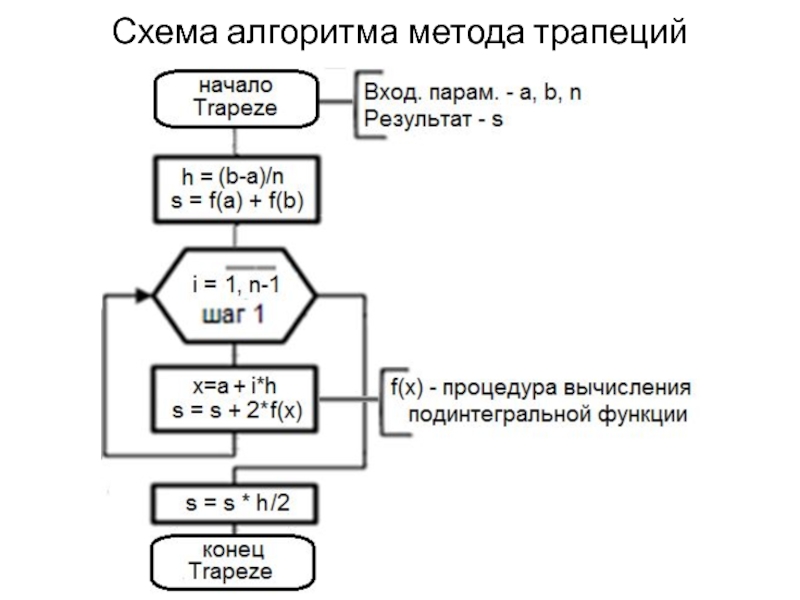
- 16. Схема алгоритма метода трапеций
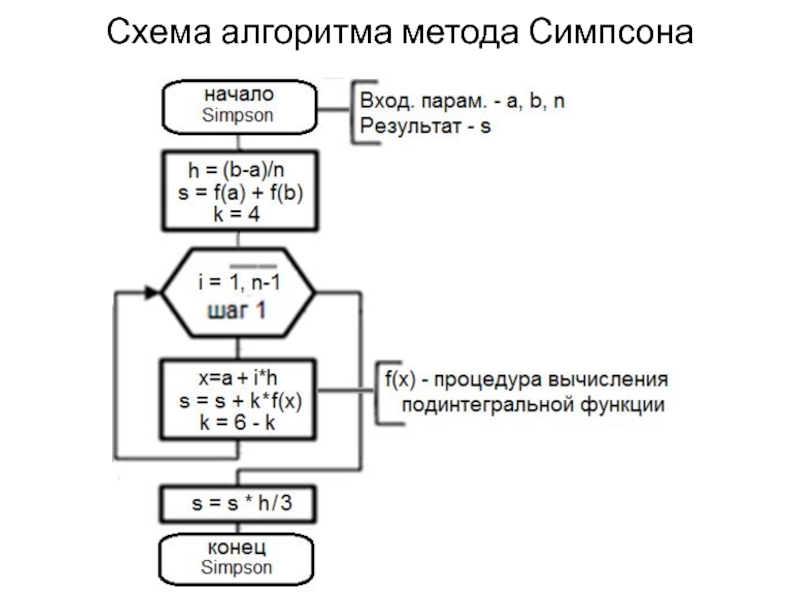
- 17. Метод Симпсона В методе Симпсона применяется интерполирующий
- 18. Метод Симпсона
- 19. Вывод формулы Симпсона
- 20. Вывод формулы Симпсона
- 21. Схема алгоритма метода Симпсона
- 22. Погрешности численного интегрирования Замена подинтегральной функции интерполяционным
- 23. Оценки погрешности численного интегрирования
- 24. Сравнение погрешностей методов Из приведенных формул видно,
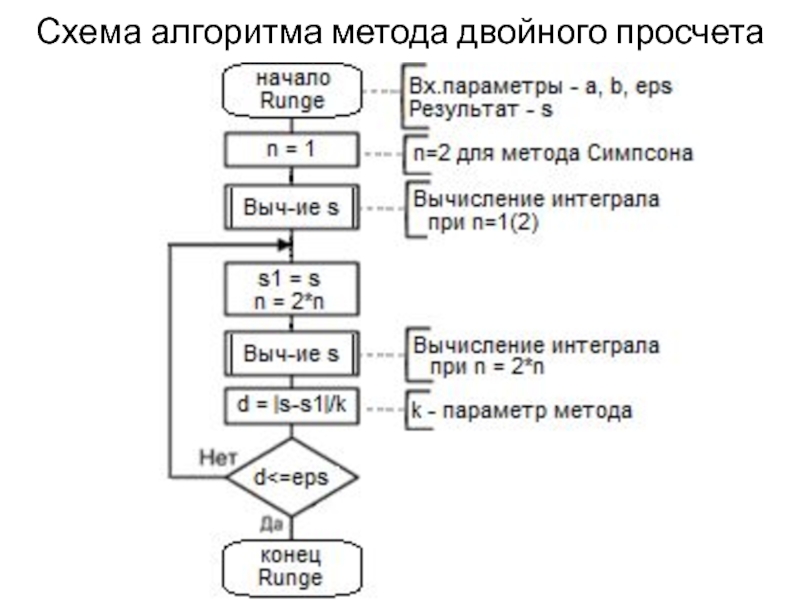
- 25. Метод двойного просчета (правило Рунге)
- 26. Схема алгоритма метода двойного просчета
Слайд 1Лекция 5
Постановка задачи численного интегрирования
Методы прямоугольников
Метод трапеций
Метод Симпсона
Погрешности численного интегрирования. Правило
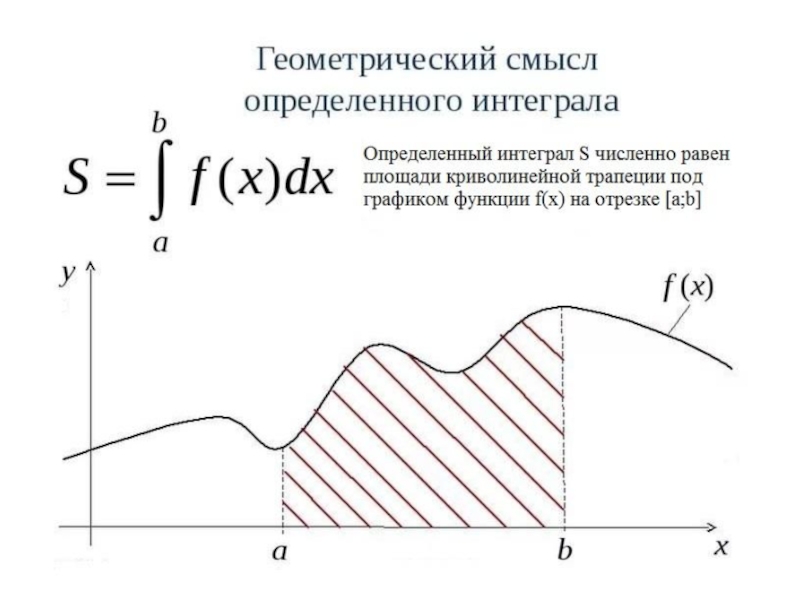
Слайд 2Определенный интеграл
Из курса математического анализа известно, что, если функция f(x) непрерывна
на отрезке [a;b] и дифференцируема, то определенный интеграл от этой функции в пределах от a до b существует и может быть вычислен по формуле Ньютона-Лейбница:
Слайд 5Приближенное вычисление площади криволинейной трапеции
Для приближенного вычисления этой площади отрезок [a;b]
разбивается на n частей, внутри которых подинтегральная функция f(x) заменяется с некоторой степенью точности более простыми функциями gi(x), которые могут быть проинтегрированы аналитически. Тогда
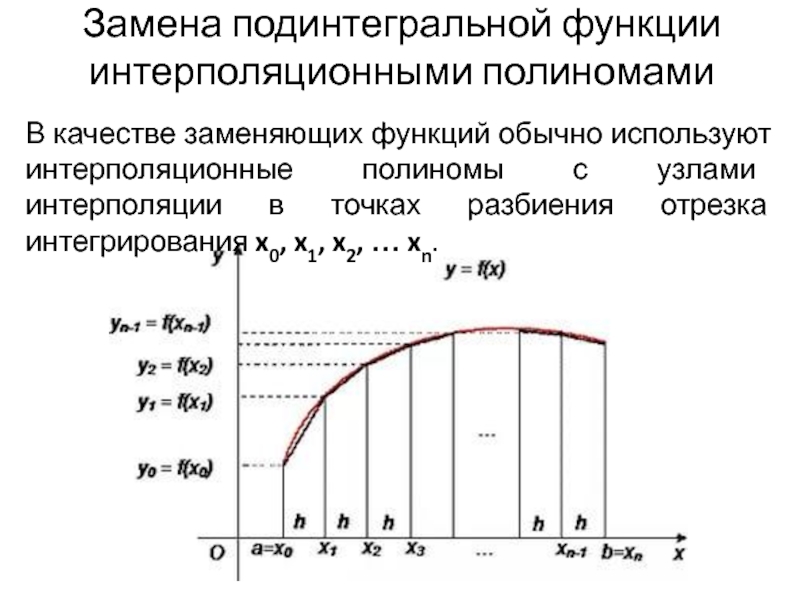
Слайд 6Замена подинтегральной функции интерполяционными полиномами
В качестве заменяющих функций обычно используют интерполяционные
полиномы с узлами интерполяции в точках разбиения отрезка интегрирования x0, x1, x2, … xn.
Слайд 7Методы численного интегрирования
Для получения простых формул используют полиномы нулевой, первой и
второй степени и, соответственно, получают следующие методы и формулы численного интегрирования:
методы прямоугольников;
метод трапеций;
метод Симпсона.
Очевидно, что во всех случаях замена функции f(x) интерполирующим полиномом приводит к образованию погрешности вычисления значения интеграла. Увеличение числа отрезков разбиения n (уменьшение длины шага интегрирования h) ведет к уменьшению погрешности.
методы прямоугольников;
метод трапеций;
метод Симпсона.
Очевидно, что во всех случаях замена функции f(x) интерполирующим полиномом приводит к образованию погрешности вычисления значения интеграла. Увеличение числа отрезков разбиения n (уменьшение длины шага интегрирования h) ведет к уменьшению погрешности.
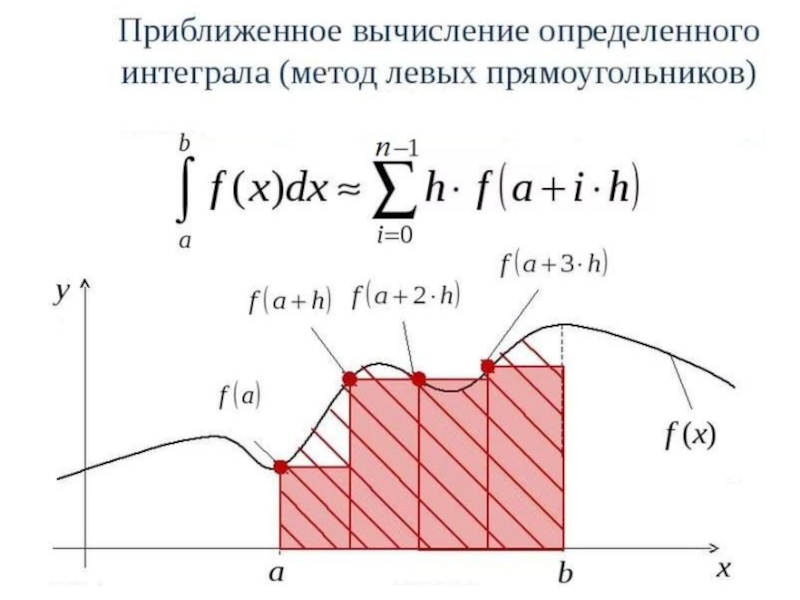
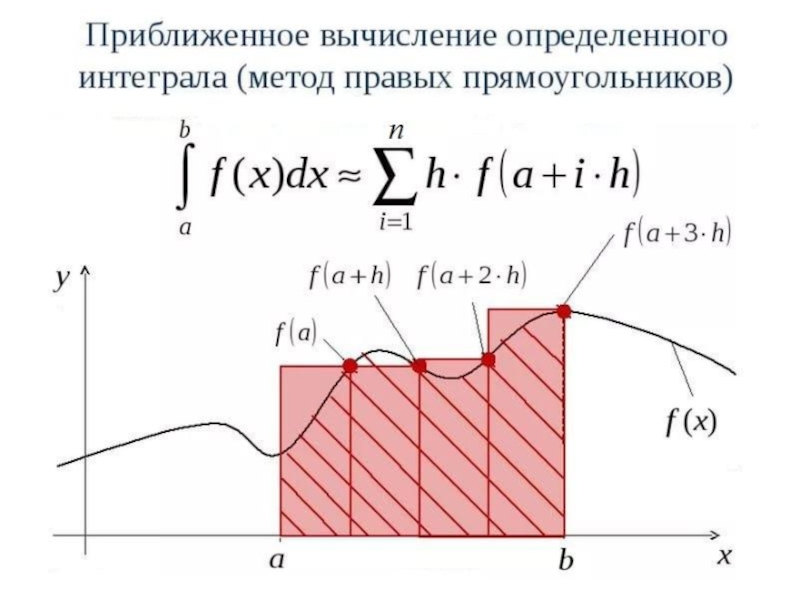
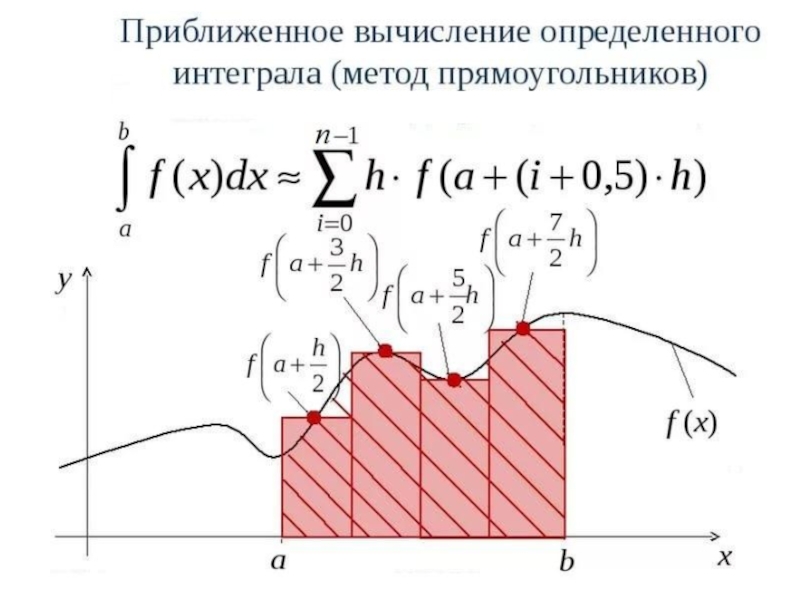
Слайд 8Методы прямоугольников
В методах прямоугольников подинтегральная функция f(x) заменяется в пределах каждого
элементарного отрезка [xi;xi+1] интерполяционным полиномом нулевой степени, то есть постоянной величиной. При этом значение элементарного интеграла равно площади прямоугольника, а интеграл на отрезке [a;b] – сумме этих площадей.
Если в качестве значения подинтегральной функции берется ее значение в левом конце отрезка, то получается формула левых прямоугольников. При использовании значения подинтегральной функции в правом конце отрезка получается формула правых прямоугольников.
При одном и том же числе отрезков разбиения n большую точность дает метод средних прямоугольников, в котором используется значение подинтегральной функции в середине отрезка. Поскольку объем вычислений во всех трех случаях одинаков, то более предпочтительым оказывается метод средних прямоугольников, который часто называют просто методом прямоугольников.
Если в качестве значения подинтегральной функции берется ее значение в левом конце отрезка, то получается формула левых прямоугольников. При использовании значения подинтегральной функции в правом конце отрезка получается формула правых прямоугольников.
При одном и том же числе отрезков разбиения n большую точность дает метод средних прямоугольников, в котором используется значение подинтегральной функции в середине отрезка. Поскольку объем вычислений во всех трех случаях одинаков, то более предпочтительым оказывается метод средних прямоугольников, который часто называют просто методом прямоугольников.
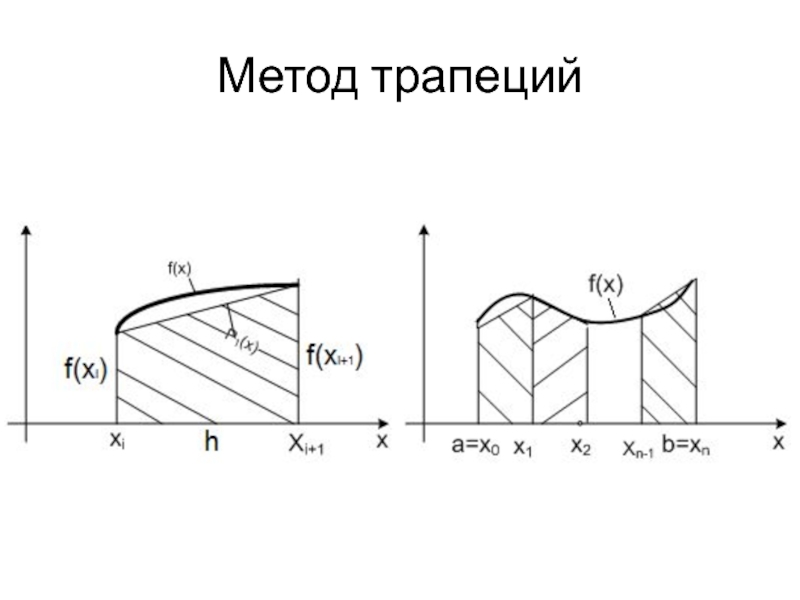
Слайд 13Метод трапеций
В методе трапеций подинтегральная функция f(x) на каждом элементарном отрезке
[xi;xi+1] заменяется интерполяционным полиномом первой степени. При этом значение элементарного интеграла равно площади прямоугольной трапеции с высотой h и основаниями f(xi) и f(xi+1), а интеграл на отрезке [a;b] – сумме этих площадей.
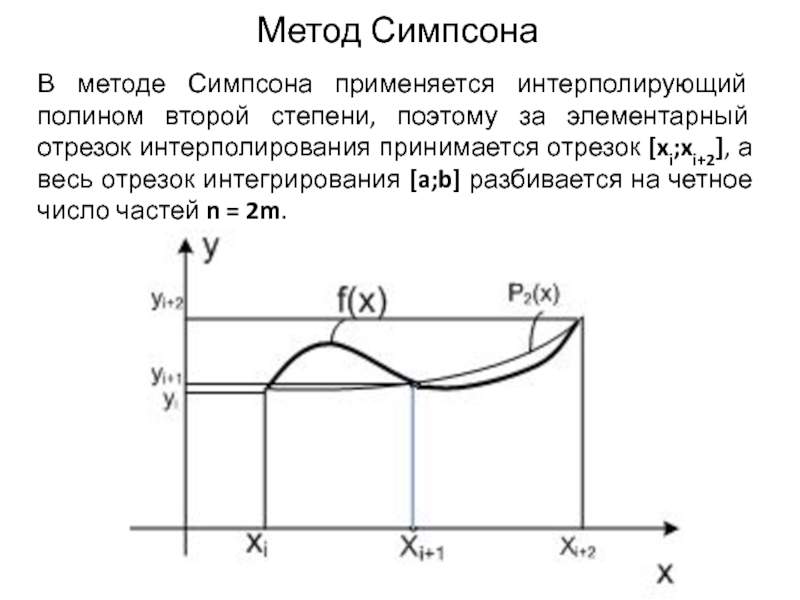
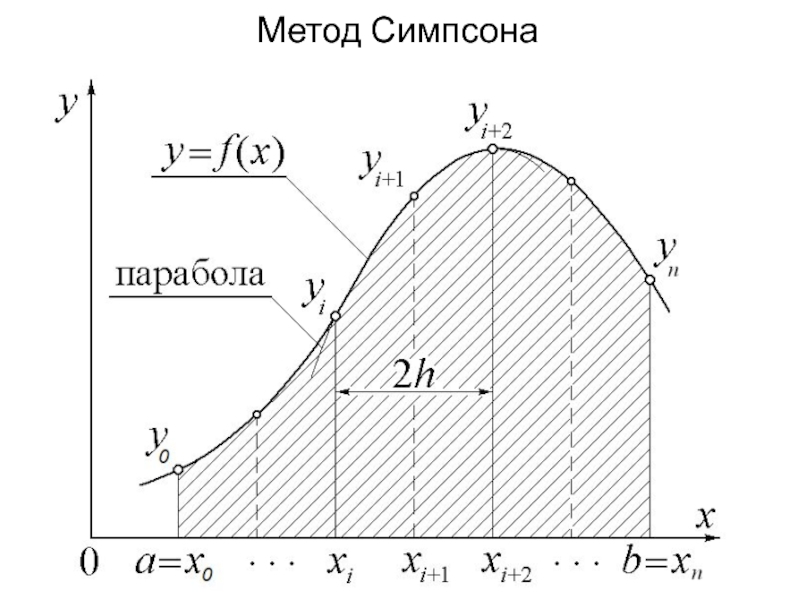
Слайд 17Метод Симпсона
В методе Симпсона применяется интерполирующий полином второй степени, поэтому за
элементарный отрезок интерполирования принимается отрезок [xi;xi+2], а весь отрезок интегрирования [a;b] разбивается на четное число частей n = 2m.
Слайд 22Погрешности численного интегрирования
Замена подинтегральной функции интерполяционным полиномом приводит к погрешности вычисления
определенного интеграла
R = |S – S*|, где S* – точное значение интеграла.
Имеются следующие оценки этой погрешности для рассмотренных нами методов и случаев аналитического или табличного задания подинтегральной функции:
R = |S – S*|, где S* – точное значение интеграла.
Имеются следующие оценки этой погрешности для рассмотренных нами методов и случаев аналитического или табличного задания подинтегральной функции:
Слайд 24Сравнение погрешностей методов
Из приведенных формул видно, что уменьшение шага интегрирования h
приводит к уменьшению погрешности. Метод Симпсона при шаге h дает примерно ту же точность, что и методы прямоугольников и трапеций при шаге h/2, а при одинаковой точности метод Симпсона требует примерно вдвое меньше вычислений.

![Определенный интегралИз курса математического анализа известно, что, если функция f(x) непрерывна на отрезке [a;b] и](/img/tmb/3/289821/3331b67ea645d86aa7a7872359066faf-800x.jpg)

![Приближенное вычисление площади криволинейной трапецииДля приближенного вычисления этой площади отрезок [a;b] разбивается на n частей,](/img/tmb/3/289821/f15627130a3606d44d240cc03c943ca1-800x.jpg)

![Методы прямоугольниковВ методах прямоугольников подинтегральная функция f(x) заменяется в пределах каждого элементарного отрезка [xi;xi+1] интерполяционным](/img/tmb/3/289821/8d2ff40626224e3bb43b4abe75734a0a-800x.jpg)
![Метод трапецийВ методе трапеций подинтегральная функция f(x) на каждом элементарном отрезке [xi;xi+1] заменяется интерполяционным полиномом](/img/tmb/3/289821/27945ea595f8546d83654358b4cc848d-800x.jpg)