- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамические ряды. Показатели динамики презентация
Содержание
- 1. Динамические ряды. Показатели динамики
- 2. Динамические ряды состоят из двух элементов: из
- 4. Значения
- 5. Показатели динамики Средний уровень ряда
- 6. Пример 2. Данные о количестве
- 7. Расчет среднего уровня ряда для моментных динамических
- 8. Уровни ряда С равными интервалами – С неравными интервалами –
- 9. Абсолютный прирост Абсолютный прирост показывает на сколько
- 10. Абсолютный прирост равный разности между текущим периодом
- 11. Средний абсолютный прирост определим через накопленный (базисный)
- 12. Темп роста показывает, во сколько раз сравниваемый
- 13. Средний темп роста – обобщающая характеристика индивидуальных
- 14. Пример. Розничный товарооборот магазина составил
- 15. Темп прироста – характеризует абсолютный прирост в
- 16. Если темп прироста выражен в
- 17. Для определения среднего темпа прироста применяется формула
Слайд 1Динамические ряды. Показатели динамики.
Ряды статистических величин, характеризующие изменение явления во времени,
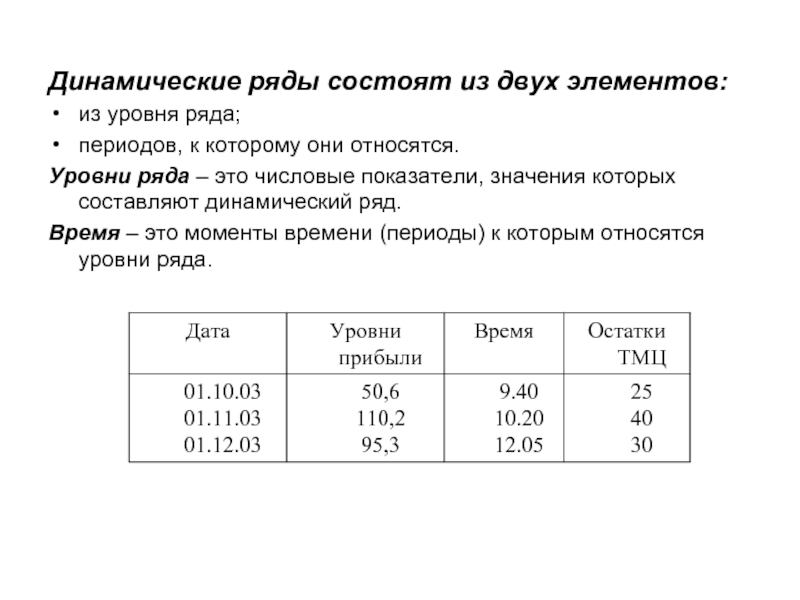
Слайд 2Динамические ряды состоят из двух элементов:
из уровня ряда;
периодов, к которому они
Уровни ряда – это числовые показатели, значения которых составляют динамический ряд.
Время – это моменты времени (периоды) к которым относятся уровни ряда.
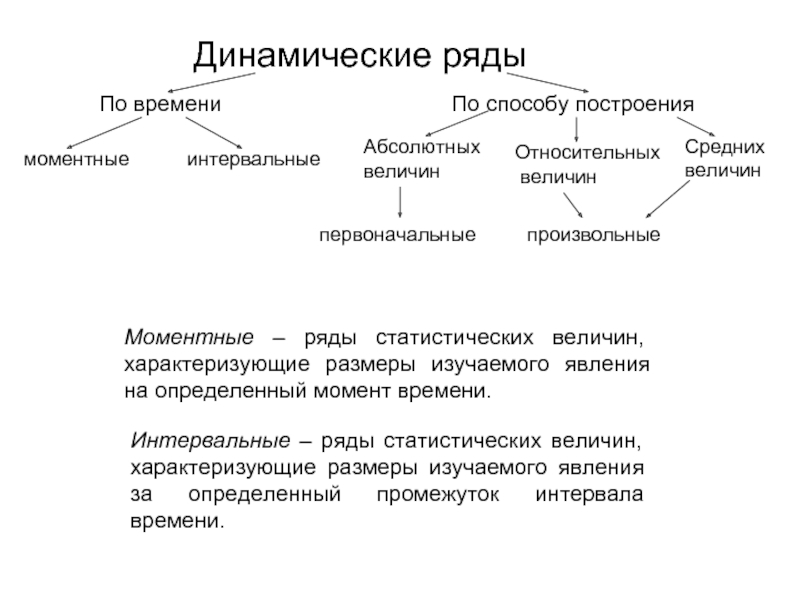
Слайд 3 Динамические ряды
По времени
По способу построения
моментные
интервальные
Абсолютных
величин
Относительных
величин
Средних
величин
первоначальные
произвольные
Моментные – ряды статистических величин, характеризующие размеры изучаемого явления на определенный момент времени.
Интервальные – ряды статистических величин, характеризующие размеры изучаемого явления за определенный промежуток интервала времени.
Слайд 4 Значения динамических рядов
Динамические ряды
Динамические ряды позволяют определить направление изменения статистических показателей.
Динамические ряды позволяют определить темп изменения, т.е. как быстро происходит изменение тех или иных статистических показателей.
Ряды динамики могут быть изображены графически.
Слайд 5Показатели динамики
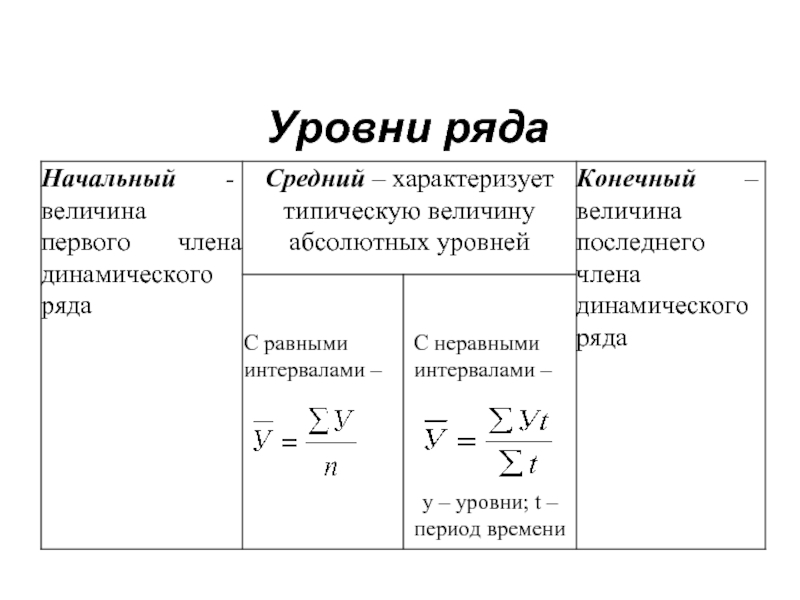
Средний уровень ряда представляет собой среднюю величину, рассчитываемую
Для интервальных динамических рядов средний уровень ряда определяется по формуле средней арифметической.
В рядах с равными интервалами - по формуле средней арифметической простой.
В рядах с неравными интервалами – средней арифметической взвешенной.
Пример 1.
Слайд 6
Пример 2. Данные о количестве произведенной продукции составили среднемесячное производство за
Слайд 7Расчет среднего уровня ряда для моментных динамических рядов.
Пример. Численность рабочих на
Средняя численность за квартал:
Средняя численность:
За январь
За февраль
За март
- средняя хронологическая
Слайд 9Абсолютный прирост
Абсолютный прирост показывает на сколько единиц увеличивается или уменьшается уровень
Слайд 10Абсолютный прирост равный разности между текущим периодом времени и предыдущим называется
- цепной абсолютный прирост
Абсолютный прирост разности данного уровня с базисным называется базисным абсолютным приростом.
- базисный абсолютный прирост
3. Общий прирост за весь промежуток времени:
4. Средний абсолютный прирост равен частному отношению суммы всех цепных абсолютных приростов на их общее число.
- средний абсолютный прирост
Слайд 11Средний абсолютный прирост определим через накопленный (базисный) абсолютный прирост.
где m – число уровней ряда динамики в изучаемом периоде, включая базисный.
Слайд 12Темп роста показывает, во сколько раз сравниваемый (текущий уровень) больше или
Если сравниваемый уровень берется по отношению к базисному уровню, то получаемый рост называется базисным.
Если сравнение происходит с предыдущим уровнем, то получаемый темп роста называется цепным.
Слайд 13Средний темп роста – обобщающая характеристика индивидуальных темпов роста ряда динамики.
Для определения среднего темпа роста применяется формула средней геометрической:
На основе взаимосвязи между цепными и базисными темпами роста средний темп роста можно определить по формуле :
где у – абсолютные уровни,
Тр – индивидуальные (цепные) темпы роста (в коэффициентах),
n – число индивидуальных темпов роста.
Слайд 14Пример.
Розничный товарооборот магазина составил в
2000
2003 г. – 1028,7; 2004 г. – 1088,4.
Тогда цепные темпы роста составили в
2001 г. – 1,053; 2003 г. – 1,050;
2002 г. – 1,051; 2004 г. – 1,058.
Средний темп роста:
или
Слайд 15Темп прироста – характеризует абсолютный прирост в относительных величинах. Исчисленный в
Базисный темп прироста вычисляется делением сравниваемого базисного абсолютного прироста на уровень, принятый за постоянную базу сравнения:
Цепной темп прироста – это отношение сравниваемого цепного абсолютного прироста к предыдущему уровню:
Слайд 16
Если темп прироста выражен в процентах, то его можно определить из
Если темп прироста выражен в коэффициентах, то его можно определить:
Слайд 17Для определения среднего темпа прироста применяется формула средней геометрической
Отношение базисных
Данный коэффициент показывает, во сколько раз быстрее растет уровень одного ряда по сравнению с другим.