- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Диференціальне числення. Визначення функції ( лекція 1.1) презентация
Содержание
- 1. Диференціальне числення. Визначення функції ( лекція 1.1)
- 2. Визначення функції Якщо кожному елементу х з
- 3. Способи задання функції Табличний спосіб. Графічний
- 4. Властивості функцій Множина усіх значень Х
- 5. Властивості функцій
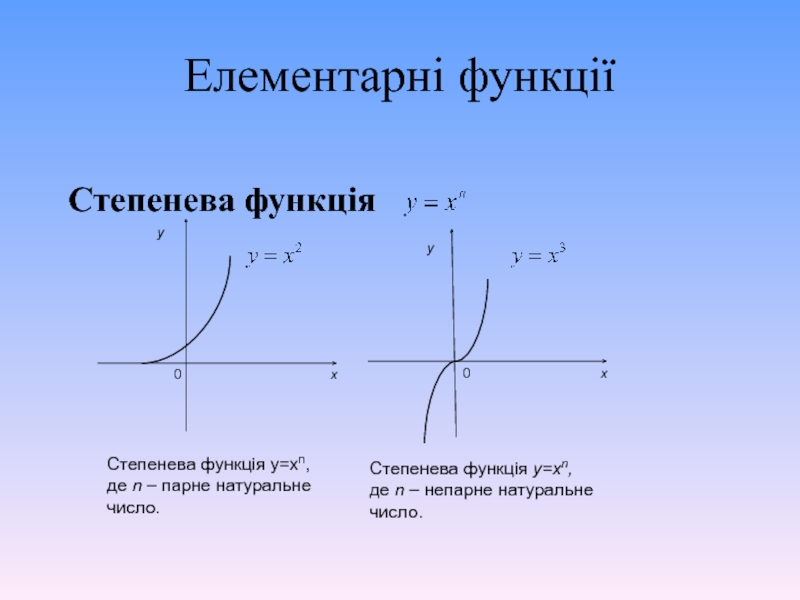
- 6. Елементарні функції Степенева функція
- 7. Елементарні функції Степенева функція: Степенева функція
- 8. Елементарні функції Лінійна функція:
- 9. Елементарні функції Показникова функція:
- 10. Елементарні функції Логарифмічна функція:
- 11. ГРАНИЦЯ ФУНКЦІЇ Графічне зображення значення функції
- 12. Теореми про границі функції
- 13. Приклади визначення границі функції №1
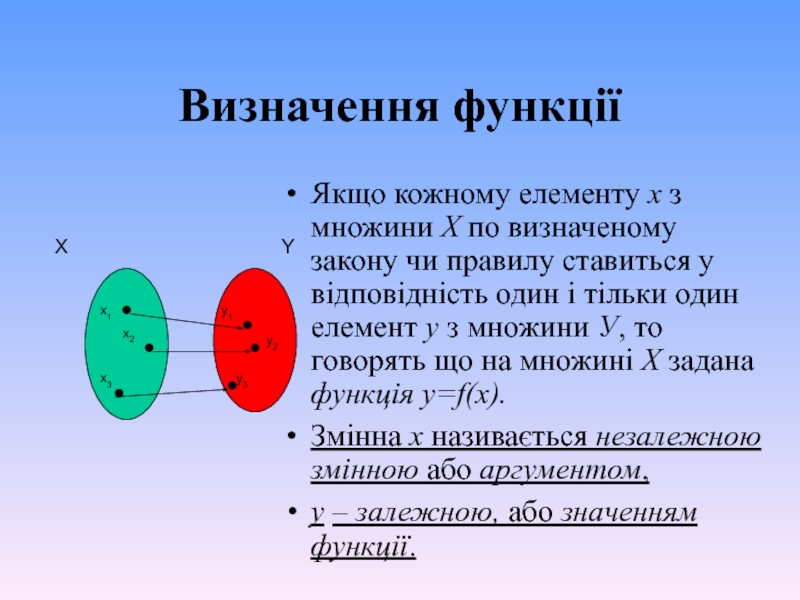
Слайд 2Визначення функції
Якщо кожному елементу х з множини Х по визначеному закону
Змінна х називається незалежною змінною або аргументом,
у – залежною, або значенням функції.
Слайд 3Способи задання функції
Табличний спосіб.
Графічний спосіб .
Аналітичний спосіб задання функції (за
- степенева функція , ;
- лінійна функція ;
- показникова функція ;
- логарифмічна функція ;
- тригонометричні функції:
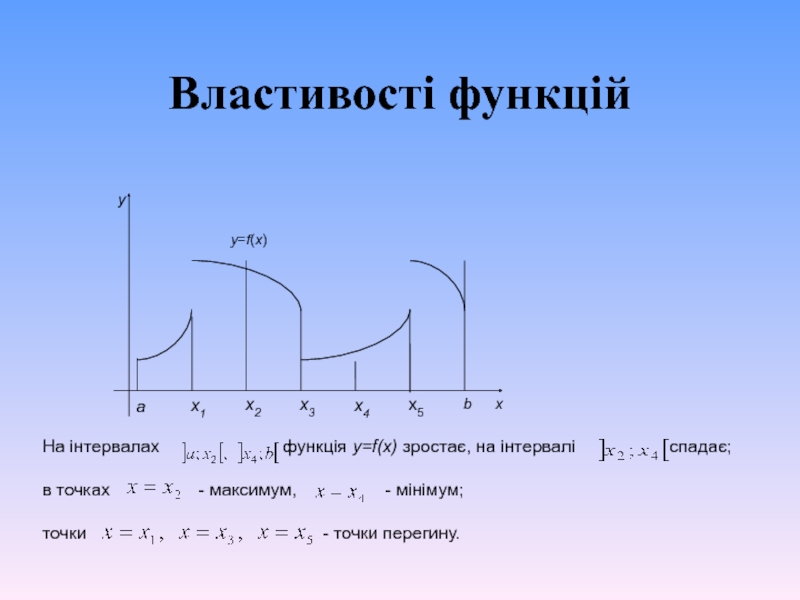
Слайд 4Властивості функцій
Множина усіх значень Х називається областю визначення функції D(f),
Функція , називається парною, якщо для будь-якого значення аргументу х з області визначення функції виконується рівність:
Функція , називається непарною, якщо для будь-якого значення х з області визначення функції виконується рівність:
Функція називається монотонно зростаючою на всій області визначення (чи на інтервалах), якщо для будь-якого значення х з області визначення функції (чи з інтервалу) виконується нерівність
Якщо за тих же умов виконується нерівність: тоді функція називається монотонно спадною.
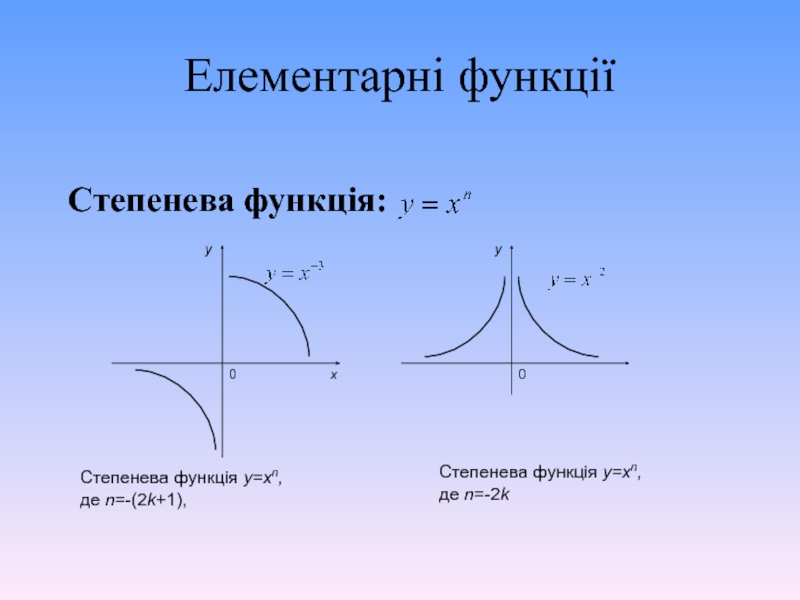
Слайд 7Елементарні функції
Степенева функція:
Степенева функція y=xn,
де n=-(2k+1),
y
0
x
Степенева функція y=xn,
де
Слайд 9Елементарні функції
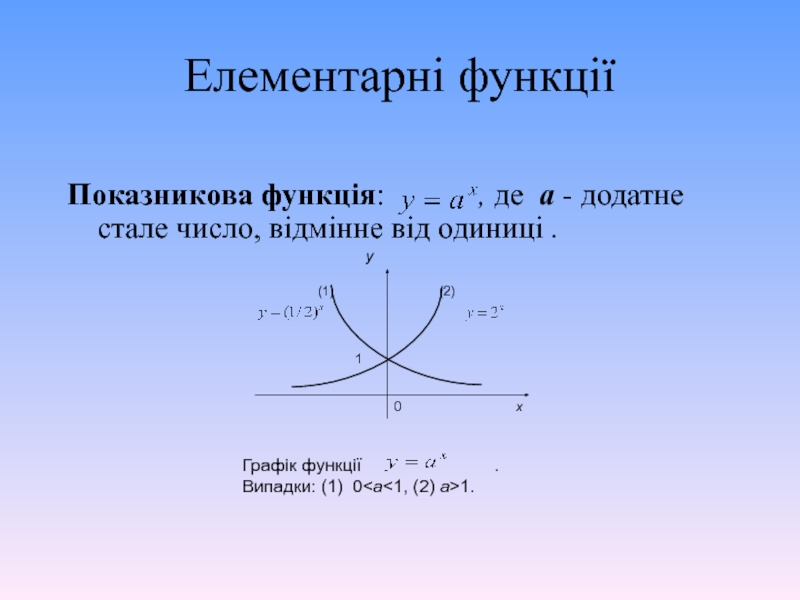
Показникова функція: , де а
Графік функції .
Випадки: (1) 0<а<1, (2) a>1.
Слайд 10Елементарні функції
Логарифмічна функція: , де
1
x
0
y
1
(2)
(1)
y=x
Графіки функції
(1) 0
Слайд 11ГРАНИЦЯ ФУНКЦІЇ
Графічне зображення значення функції f(a) та границі функції A
Число А називається границею функції f(x) при х, що прямує до а (х→ а), якщо для будь-якого як завгодно малого числа знайдеться таке мале число , що для всіх х, які задовольняють умову , виконується нерівність .
Границю функції записують у вигляді: