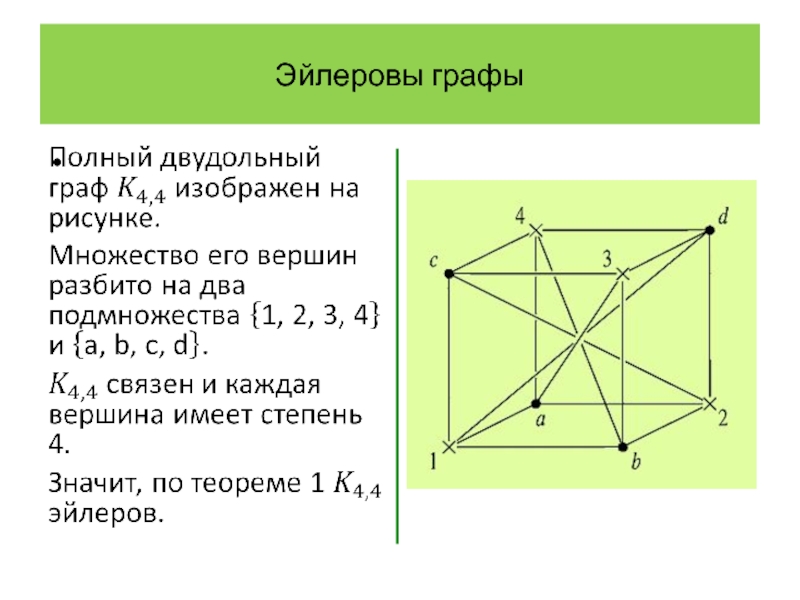
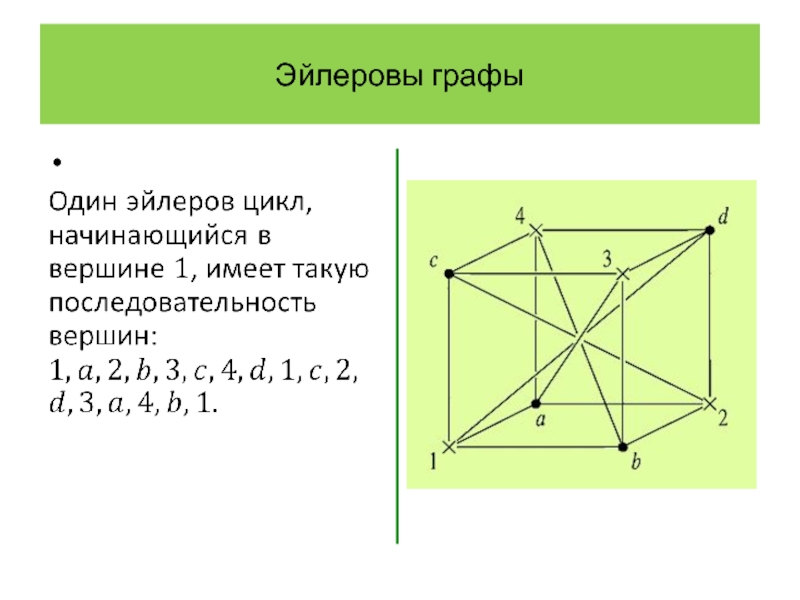
Эйлеровы графы
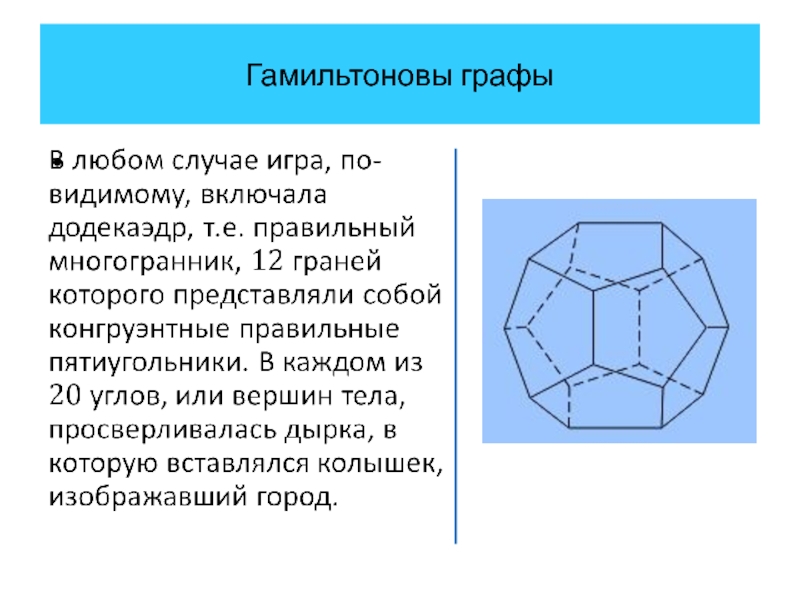
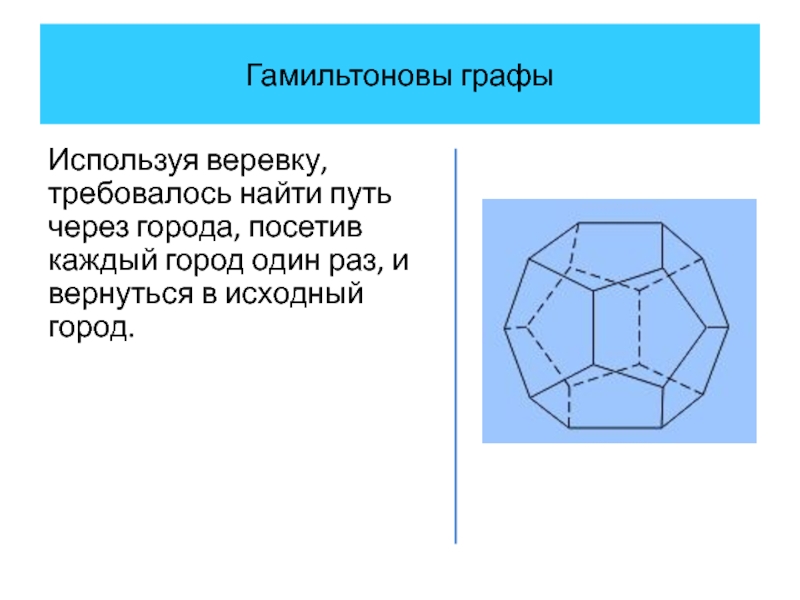
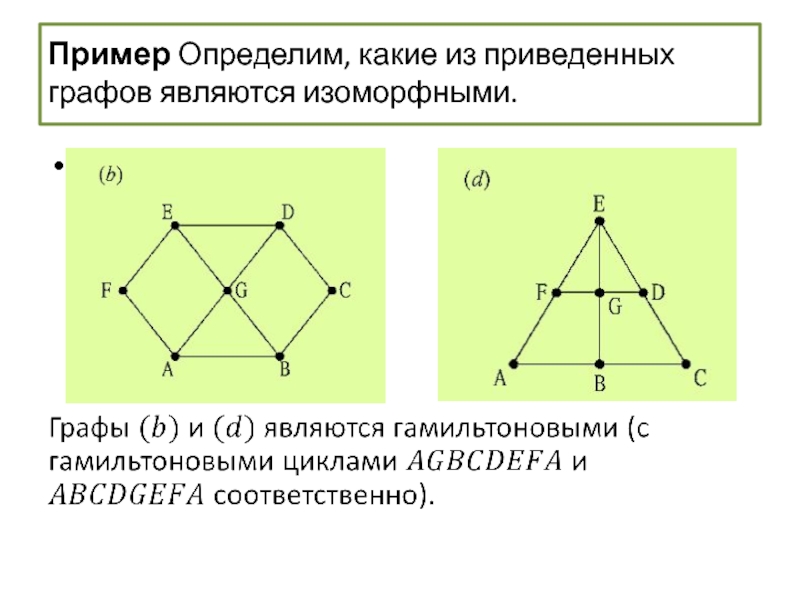
Гамильтоновы графы
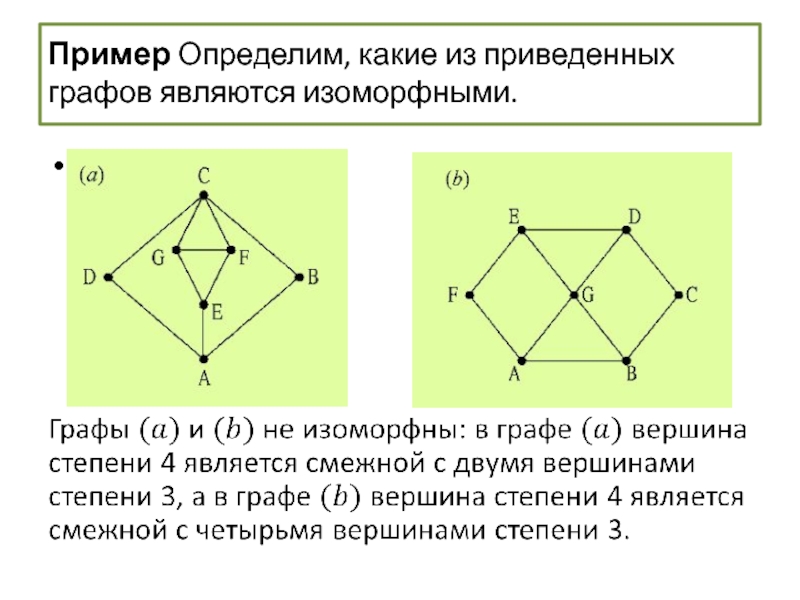
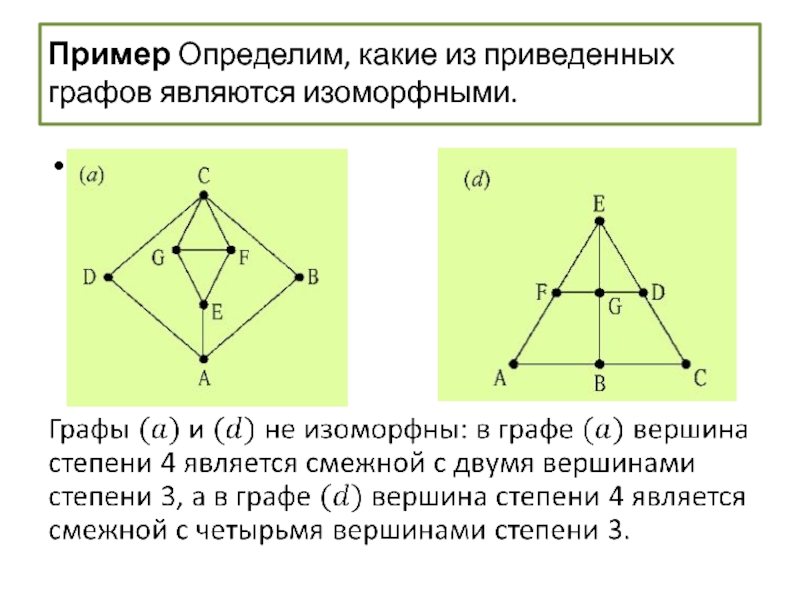
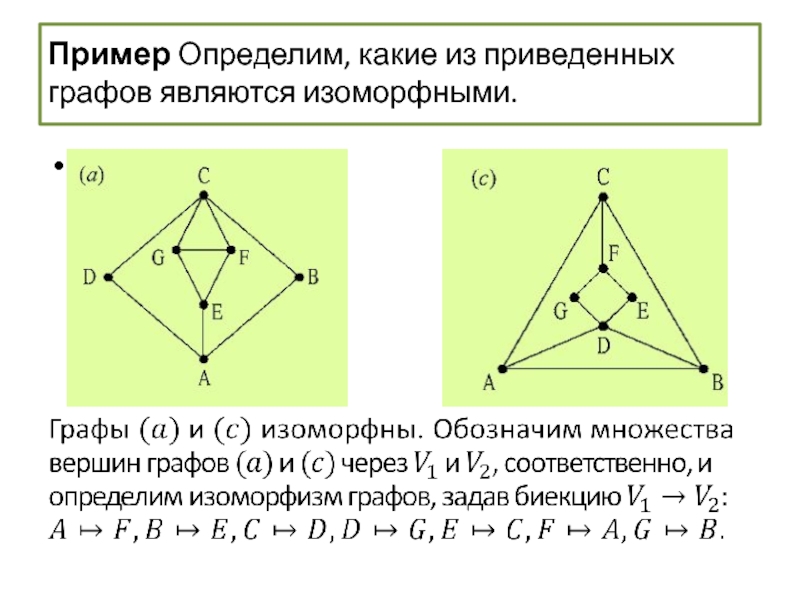
Изоморфизмы графов
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графы. Эйлеровы графы. Гамильтоновы графы. Изоморфизмы графов презентация
Содержание
- 1. Графы. Эйлеровы графы. Гамильтоновы графы. Изоморфизмы графов
- 2. Эйлеровы графы Мы уже упоминали работу Эйлера,
- 3. Эйлеровы графы Задача возникла в прусском городе
- 4. Эйлеровы графы Жители Кенигсберга интересовались, могут ли
- 5. Эйлеровы графы Жители Кенигсберга не могли найти
- 6. Эйлеровы графы
- 7. Эйлеровы графы
- 8. Эйлеровы графы
- 9. Эйлеровы графы
- 10.
- 11.
- 12.
- 13. Эйлеровы графы Жители Кенигсберга не могли найти
- 14. Эйлеровы графы
- 15. Эйлеровы графы
- 16. Эйлеровы графы
- 17. Эйлеровы графы
- 18. Эйлеровы графы
- 19. Гамильтоновы графы Эйлеров цикл проходит через каждое
- 20. Гамильтоновы графы Определение 2 Гамильтонов цикл в
- 21. Гамильтоновы графы Сэр Уильям Роуэн Гамильтон (1805
- 22. Гамильтоновы графы В 1843 он открыл кватернионы
- 23. Гамильтоновы графы Итак, в 1857 году Уильям
- 24. Гамильтоновы графы
- 25. Гамильтоновы графы Используя веревку, требовалось найти путь
- 26. Гамильтоновы графы Рассмотрим эквивалентный вопрос. Существует ли
- 27. Гамильтоновы графы Ответ на последний вопрос решает
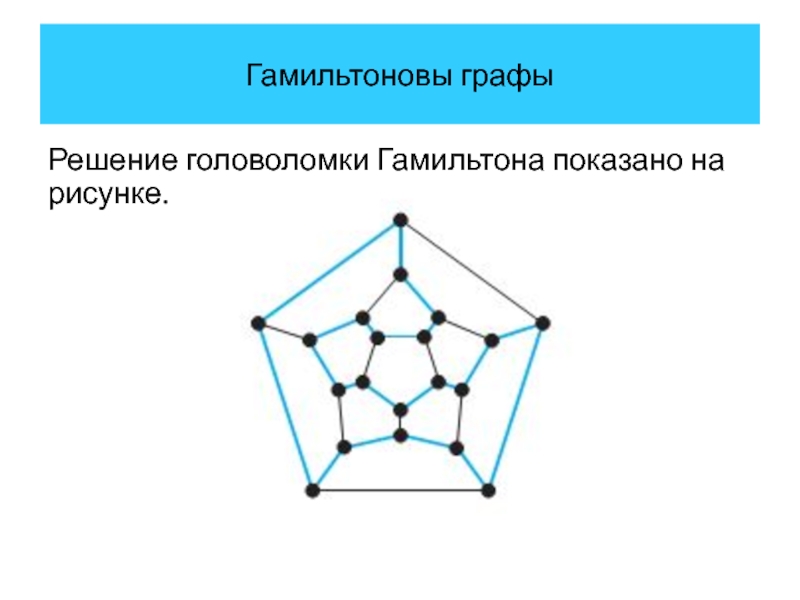
- 28. Гамильтоновы графы Решение головоломки Гамильтона показано на рисунке.
- 29. Гамильтоновы графы
- 30. Гамильтоновы графы Для эйлеровых графов имеется достаточно
- 31. Гамильтоновы графы Эта задача остается одной из
- 32. Гамильтоновы графы
- 33. Гамильтоновы графы
- 34. Гамильтоновы графы
- 35. Гамильтоновы графы В действительности, каждый из графов,
- 36. Гамильтоновы графы
- 37. Гамильтоновы графы Задача 1 Покажите, что каждый
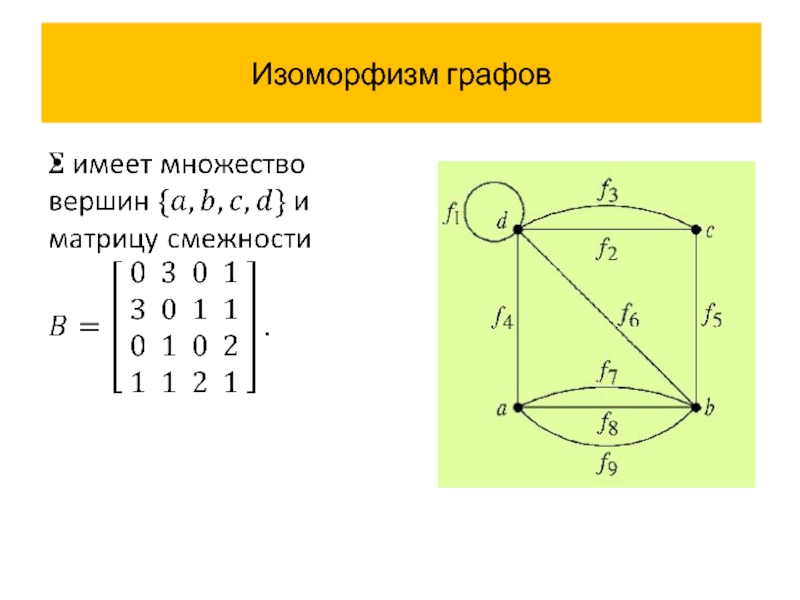
- 38. Изоморфизм графов
- 39. Изоморфизм графов
- 40. Изоморфизм графов
- 41.
- 42.
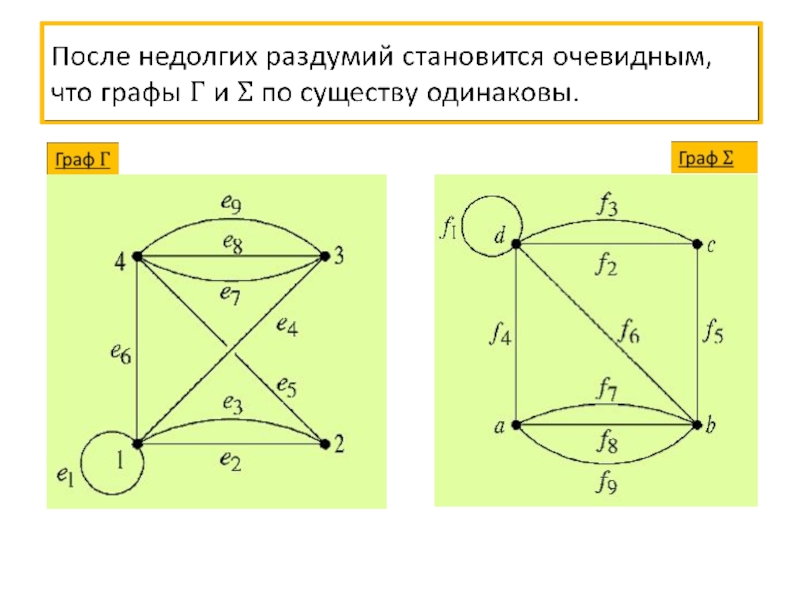
- 43. Изоморфизм графов
- 44. Изоморфизм графов
- 45. Изоморфизм графов
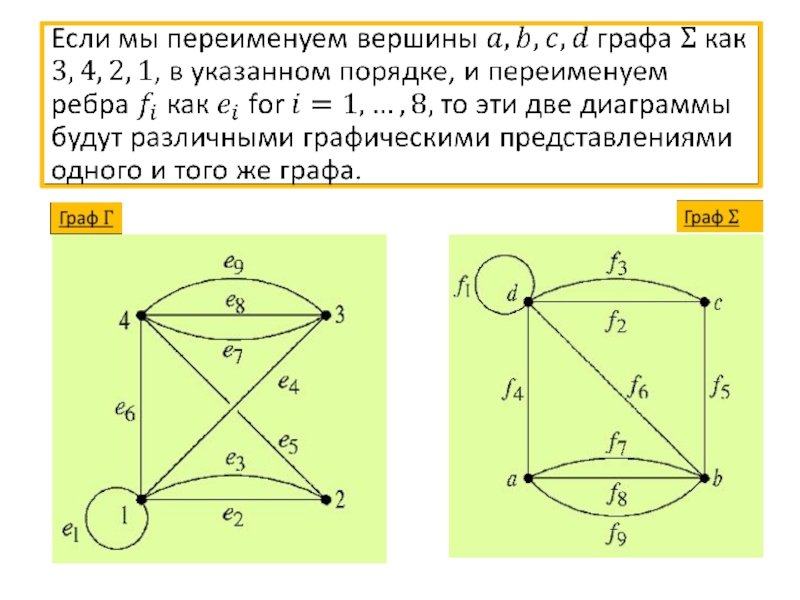
- 46. Изоморфизм графов
- 47. Изоморфизм графов
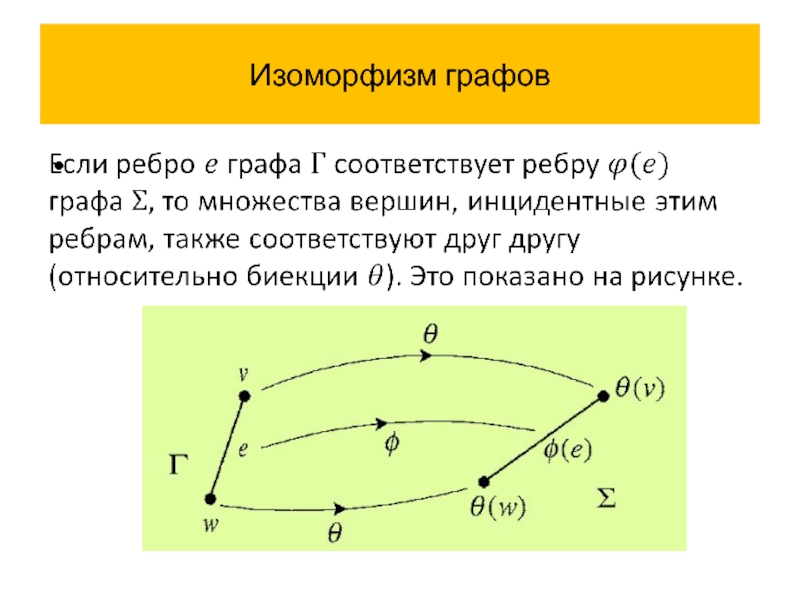
- 48. Изоморфизм графов Изоморфизм графов является отношением эквивалентности.
- 49. Изоморфизм графов Так как изоморфные графы имеют,
- 50. Изоморфизм графов
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
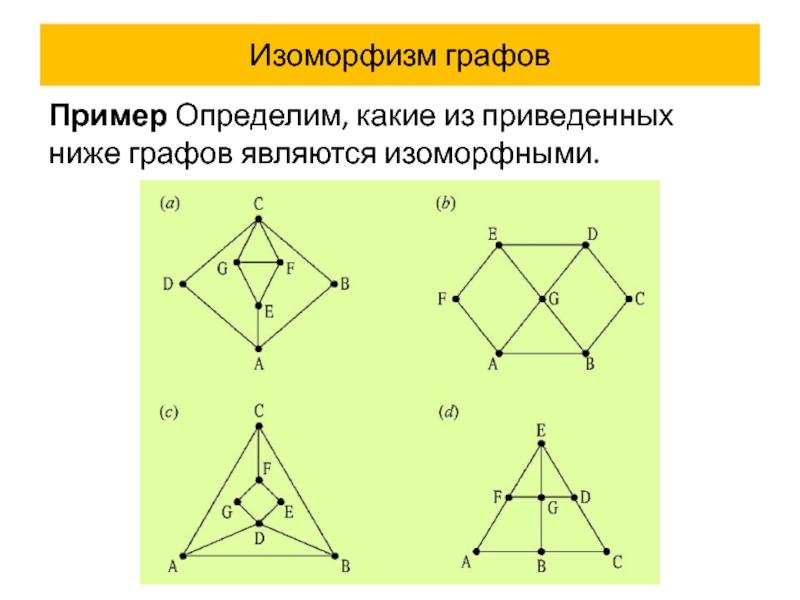
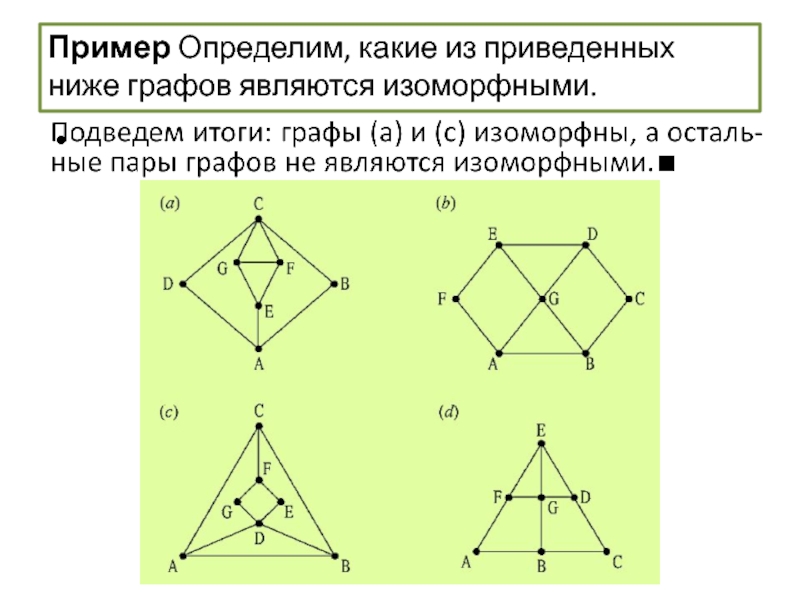
- 59. Изоморфизм графов Пример Определим, какие из приведенных ниже графов являются изоморфными.
- 60. Пример Определим, какие из приведенных ниже
- 61. Пример Определим, какие из приведенных ниже графов являются изоморфными.
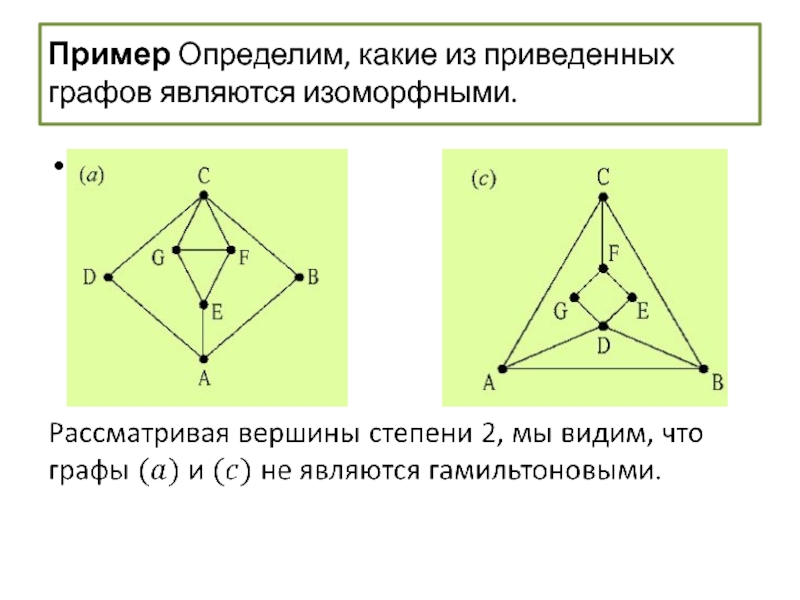
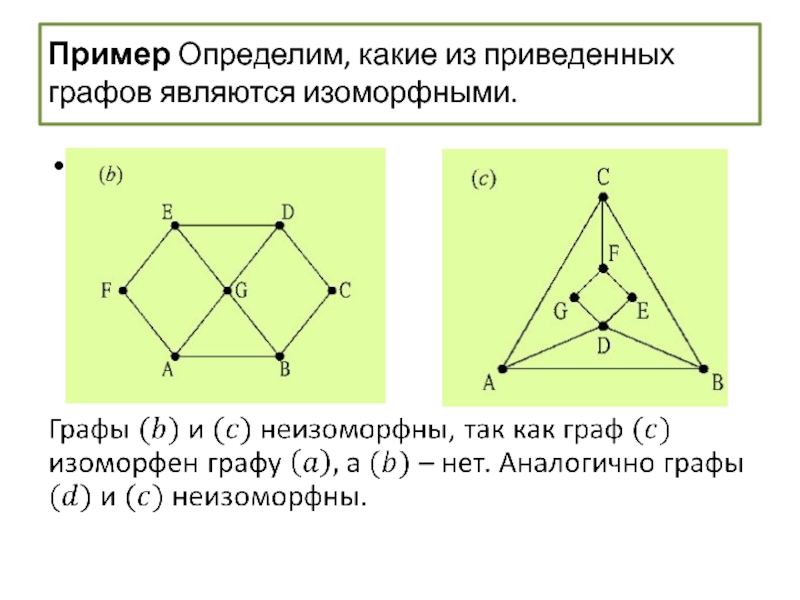
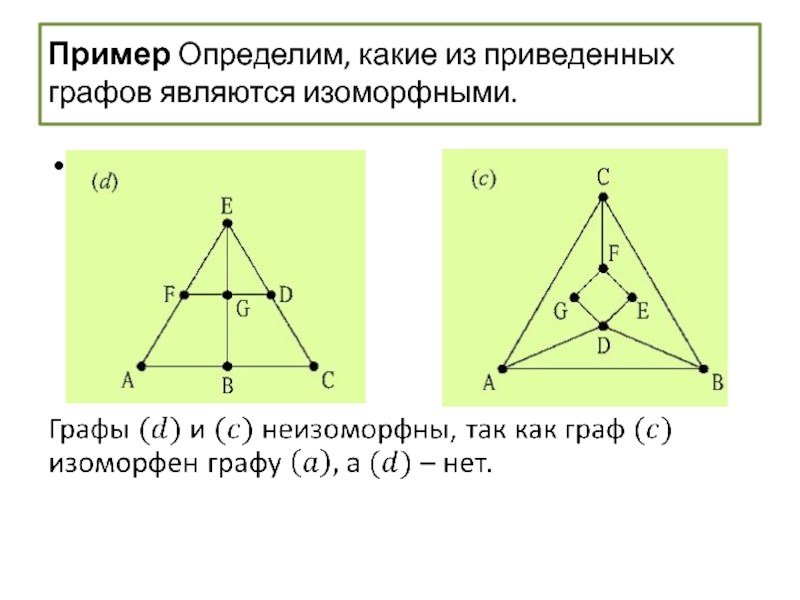
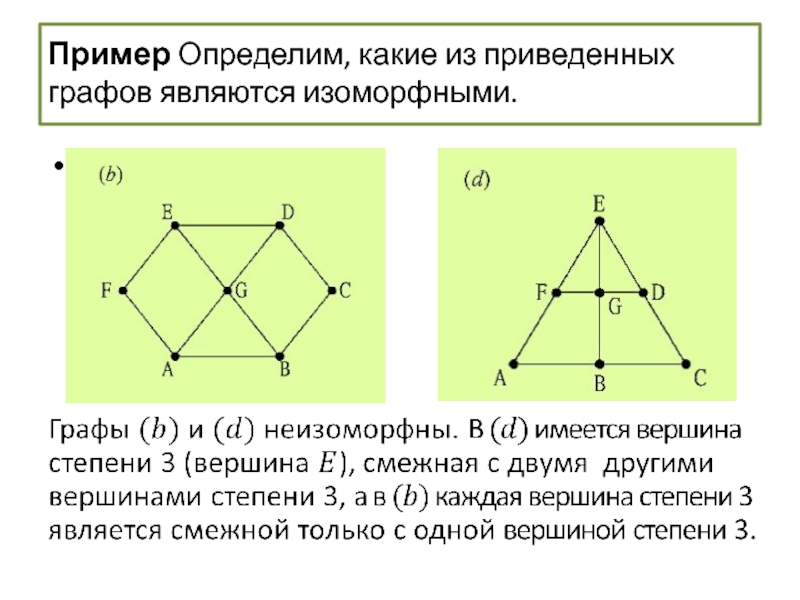
- 62. Пример Определим, какие из приведенных графов являются изоморфными.
- 63. Пример Определим, какие из приведенных графов являются изоморфными.
- 64. Пример Определим, какие из приведенных графов являются изоморфными.
- 65. Пример Определим, какие из приведенных графов являются изоморфными.
- 66. Пример Определим, какие из приведенных графов являются изоморфными.
- 67. Пример Определим, какие из приведенных графов являются изоморфными.
- 68. Пример Определим, какие из приведенных графов являются изоморфными.
- 69. Пример Определим, какие из приведенных графов являются изоморфными.
- 70. Пример Определим, какие из приведенных графов являются изоморфными.
- 71. Пример Определим, какие из приведенных ниже графов являются изоморфными.
- 72. Изоморфизм графов Принцип изоморфизма Чтобы доказать, что
Эйлеровы графы Мы уже упоминали работу Эйлера, датированную 1736 годом, которая положила начало теории графов. В этой работе Эйлер изложил теорию, позволившую решить задачу о мостах Кенигсберга. Перейдем к изложению
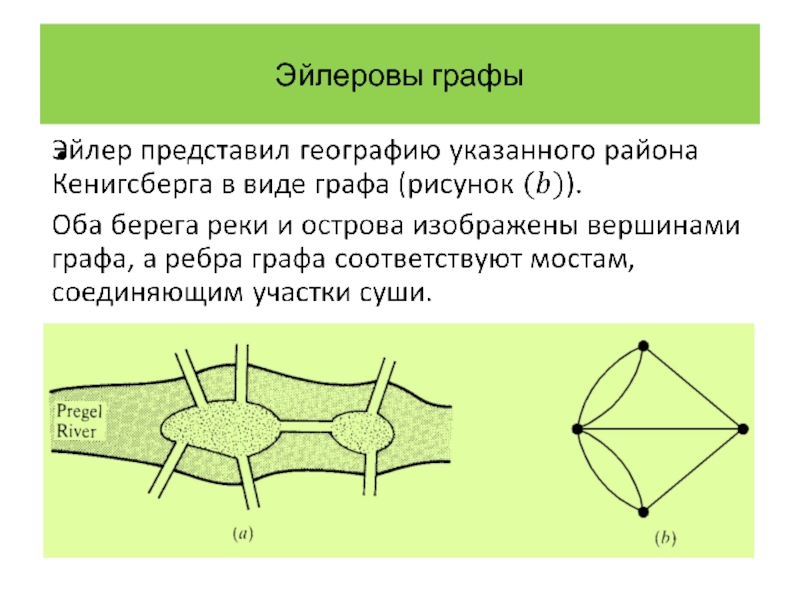
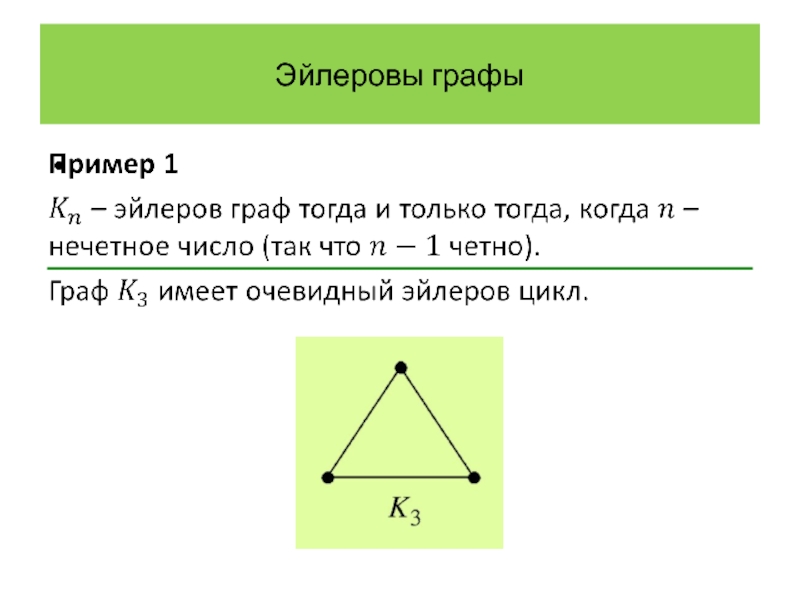
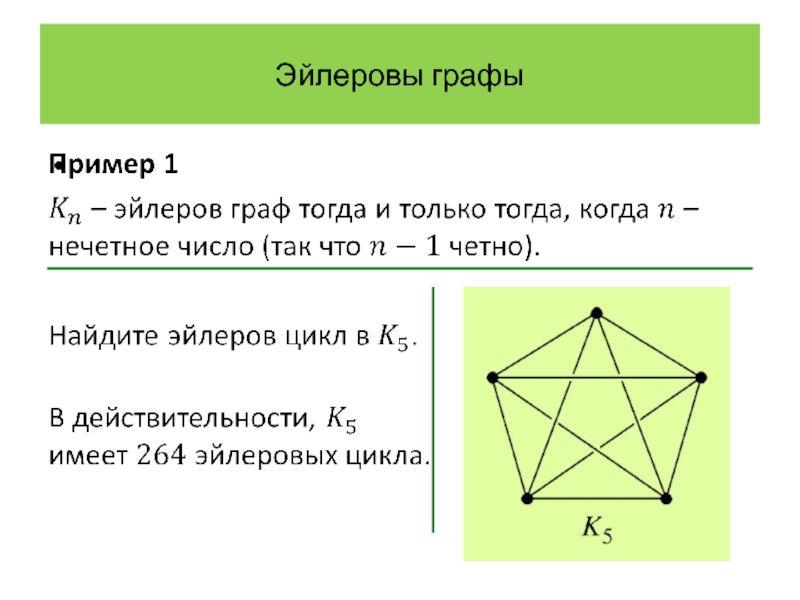
Слайд 2Эйлеровы графы
Мы уже упоминали работу Эйлера, датированную 1736 годом, которая положила
начало теории графов.
В этой работе Эйлер изложил теорию, позволившую решить задачу о мостах Кенигсберга.
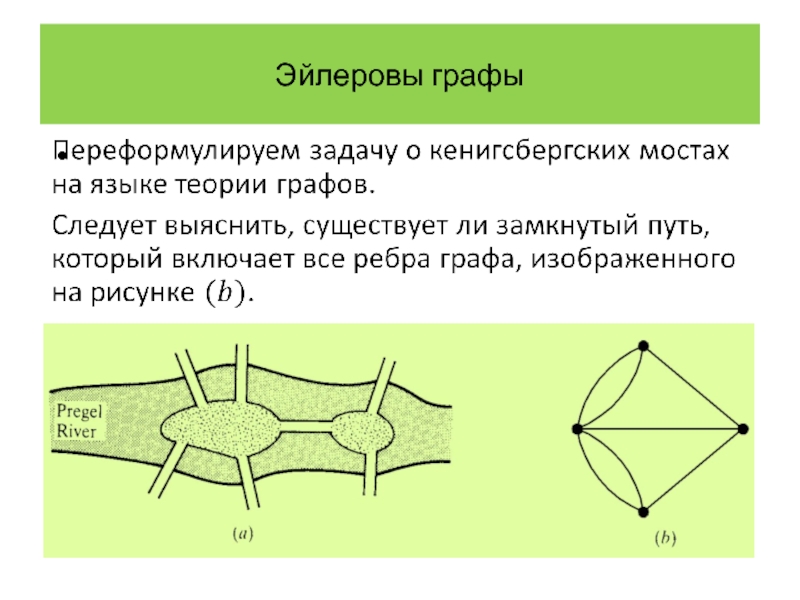
Перейдем к изложению задачи о кенигсбергских мостах. Она состоит в следующем.
В этой работе Эйлер изложил теорию, позволившую решить задачу о мостах Кенигсберга.
Перейдем к изложению задачи о кенигсбергских мостах. Она состоит в следующем.
Слайд 3Эйлеровы графы
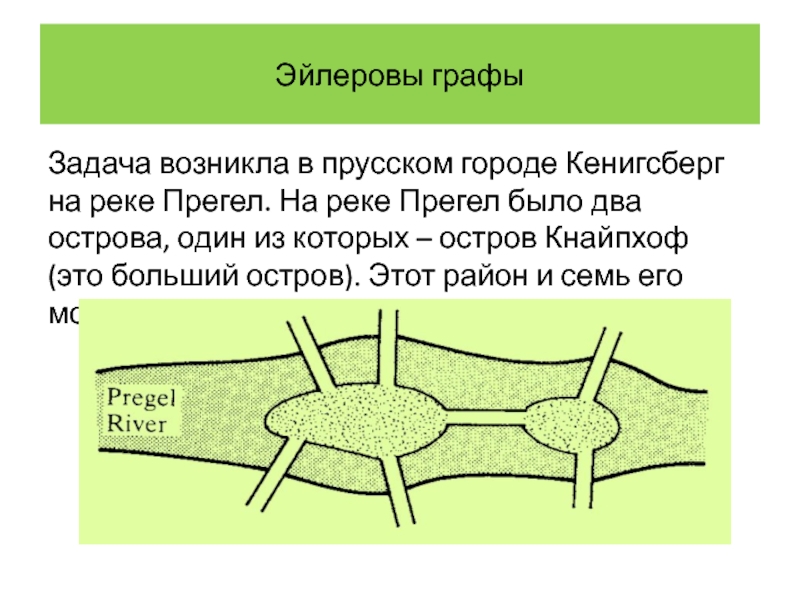
Задача возникла в прусском городе Кенигсберг на реке Прегел. На
реке Прегел было два острова, один из которых – остров Кнайпхоф (это больший остров). Этот район и семь его мостов показаны на рисунке.
Слайд 4Эйлеровы графы
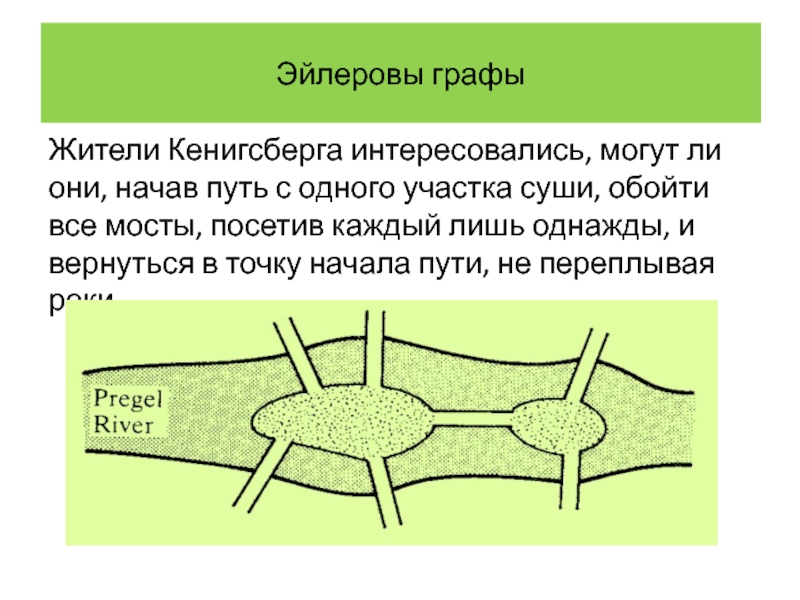
Жители Кенигсберга интересовались, могут ли они, начав путь с одного
участка суши, обойти все мосты, посетив каждый лишь однажды, и вернуться в точку начала пути, не переплывая реки.
Слайд 5Эйлеровы графы
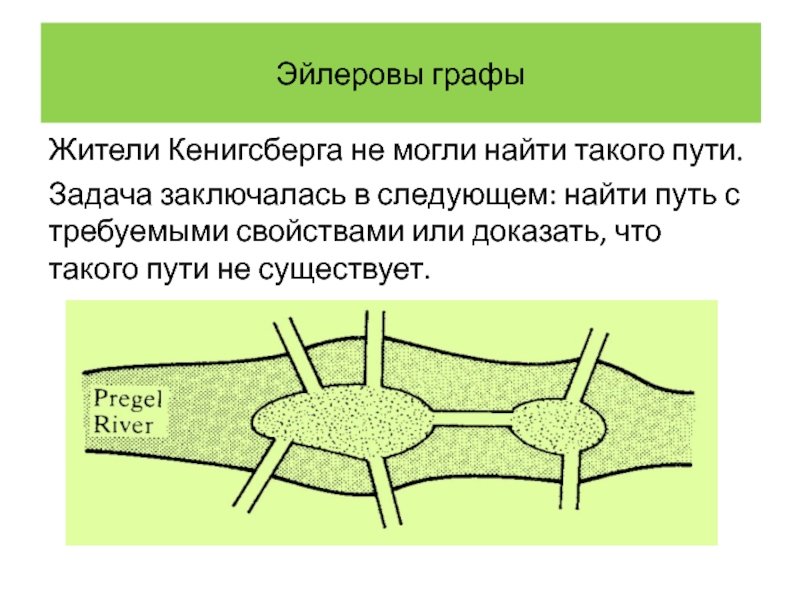
Жители Кенигсберга не могли найти такого пути.
Задача заключалась в следующем:
найти путь с требуемыми свойствами или доказать, что такого пути не существует.
Слайд 13Эйлеровы графы
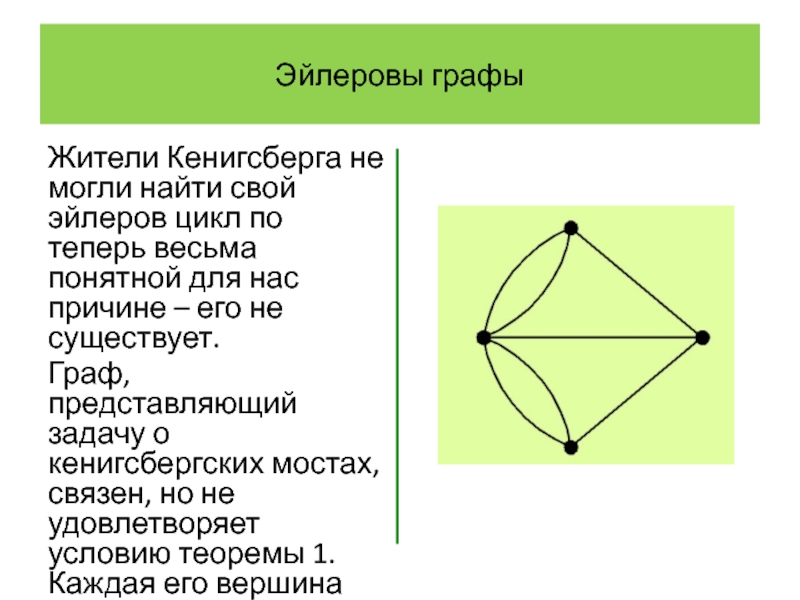
Жители Кенигсберга не могли найти свой эйлеров цикл по теперь
весьма понятной для нас причине – его не существует.
Граф, представляющий задачу о кенигсбергских мостах, связен, но не удовлетворяет условию теоремы 1. Каждая его вершина имеет нечетную степень.
Граф, представляющий задачу о кенигсбергских мостах, связен, но не удовлетворяет условию теоремы 1. Каждая его вершина имеет нечетную степень.
Слайд 19Гамильтоновы графы
Эйлеров цикл проходит через каждое ребро графа (один раз) и
возвращается в начальную точку пути.
Сформулируем аналогичную задачу: можем ли мы побывать в каждой вершине графа один раз, проходя по каждому ребру не более одного раза, и вернуться в начальную точку пути.
Этой задачей занимался Гамильтон (хотя он был не первым ее исследователем) и сегодня его имя ассоциируется с путями указанного типа.
Сформулируем аналогичную задачу: можем ли мы побывать в каждой вершине графа один раз, проходя по каждому ребру не более одного раза, и вернуться в начальную точку пути.
Этой задачей занимался Гамильтон (хотя он был не первым ее исследователем) и сегодня его имя ассоциируется с путями указанного типа.
Слайд 20Гамильтоновы графы
Определение 2
Гамильтонов цикл в графе – это цикл, который проходит
через каждую вершину графа один раз.
Граф называется гамильтоновым, если он имеет гамильтонов цикл.
Этой терминологией мы обязаны игре, изобретенной в 1857 ирландским математиком Сэром Уильямом Роуэном Гамильтоном.
Граф называется гамильтоновым, если он имеет гамильтонов цикл.
Этой терминологией мы обязаны игре, изобретенной в 1857 ирландским математиком Сэром Уильямом Роуэном Гамильтоном.
Слайд 21Гамильтоновы графы
Сэр Уильям Роуэн Гамильтон (1805 – 1865) был выдающимся ирландским
математиком. Закончив университет, в возрасте 22 лет он был избран профессором астрономии и Королевским Астрономом Ирландии.
Однако, его вклад в астрономию невелик; его наиболее значительные результаты относятся к математике и физике.
Однако, его вклад в астрономию невелик; его наиболее значительные результаты относятся к математике и физике.
Слайд 22Гамильтоновы графы
В 1843 он открыл кватернионы – одну из разновидностей обобщения
комплексных чисел – и большую часть своей жизни он посвятил их изучению. Его имя также ассоциируется с гамильтоновым оператором энергии, используемым в физике (в частности, в волновой механике).
Слайд 23Гамильтоновы графы
Итак, в 1857 году Уильям Роуэн Гамильтон придумал игру.
Существует
несколько версий того, как это произошло. По одной из версий он описал эту игру в письме к другу. Согласно другой, он действительно изобрел игру и продал ее производителю игрушек.
Слайд 25Гамильтоновы графы
Используя веревку, требовалось найти путь через города, посетив каждый город
один раз, и вернуться в исходный город.
Слайд 26Гамильтоновы графы
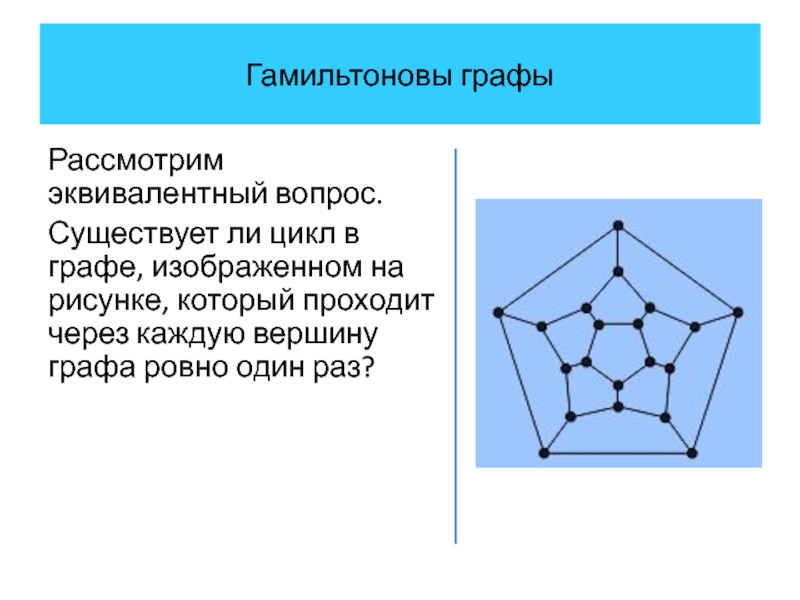
Рассмотрим эквивалентный вопрос.
Существует ли цикл в графе, изображенном на рисунке,
который проходит через каждую вершину графа ровно один раз?
Слайд 27Гамильтоновы графы
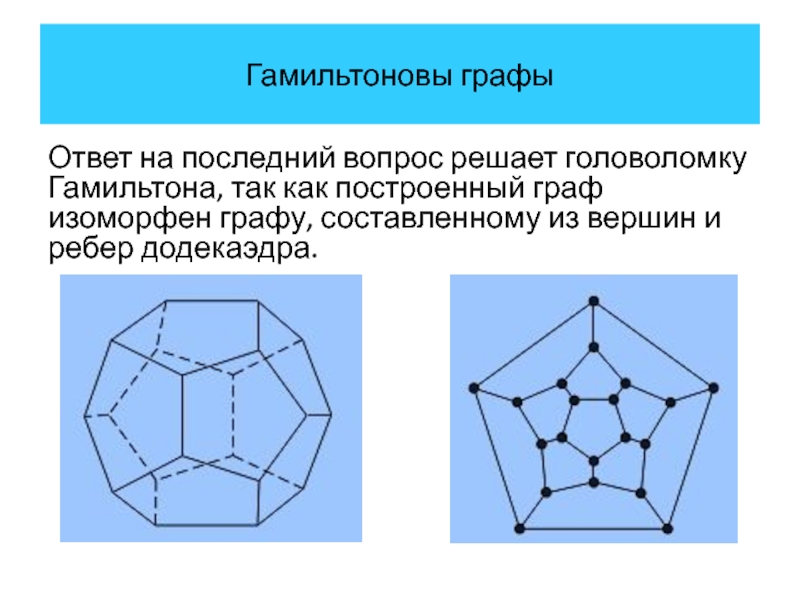
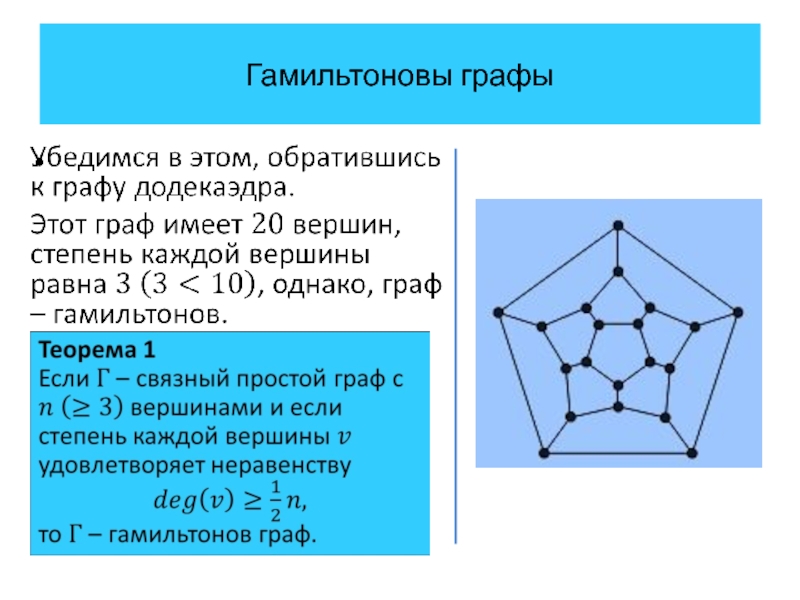
Ответ на последний вопрос решает головоломку Гамильтона, так как построенный
граф изоморфен графу, составленному из вершин и ребер додекаэдра.
Слайд 30Гамильтоновы графы
Для эйлеровых графов имеется достаточно простой критерий. Однако, не так
обстоят дела с гамильтоновыми графами.
Действительно, изучая последние графы более столетия, математики до сих пор не нашли критерия гамильтоновости графов.
(Под ‘критерием’ гамильтоновости графа мы понимаем необходимое и достаточное условия того, что граф является гамильтоновым.)
Действительно, изучая последние графы более столетия, математики до сих пор не нашли критерия гамильтоновости графов.
(Под ‘критерием’ гамильтоновости графа мы понимаем необходимое и достаточное условия того, что граф является гамильтоновым.)
Слайд 31Гамильтоновы графы
Эта задача остается одной из основных нерешенных проблем теории графов.
Очевидным
необходимым условием гамильтоновости графа является его связность.
Известны также и различные достаточные условия гамильтоновости графа.
Как правило, в достаточных условиях гамильтоновости графа требуется, чтобы граф имел ‘достаточно’ ребер в определенном смысле этого слова.
Известны также и различные достаточные условия гамильтоновости графа.
Как правило, в достаточных условиях гамильтоновости графа требуется, чтобы граф имел ‘достаточно’ ребер в определенном смысле этого слова.
Слайд 35Гамильтоновы графы
В действительности, каждый из графов, связанных с пятью правильными многогранниками,
имеет гамильтонов цикл.
Слайд 37Гамильтоновы графы
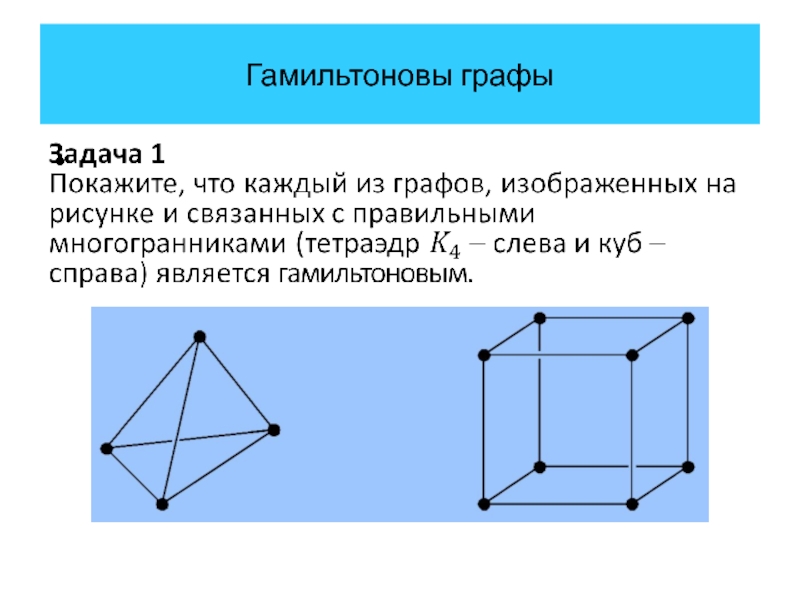
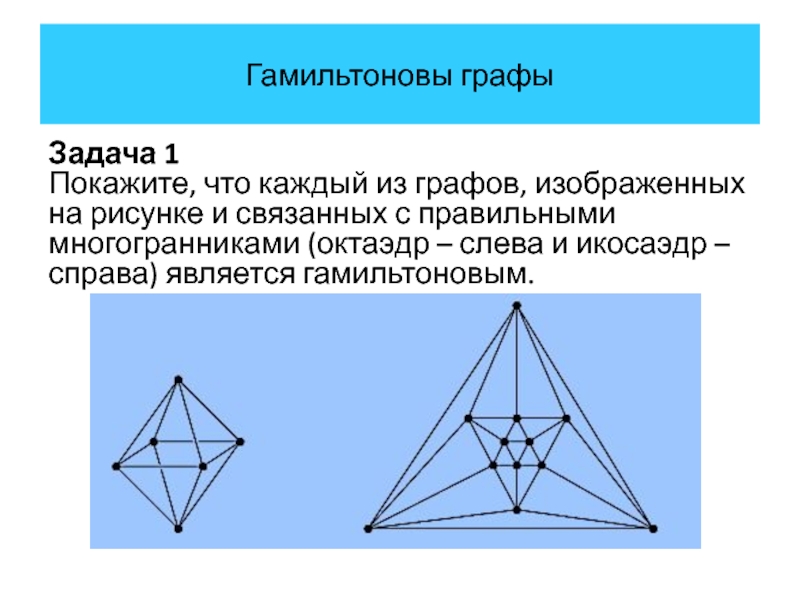
Задача 1
Покажите, что каждый из графов, изображенных на рисунке и
связанных с правильными многогранниками (октаэдр – слева и икосаэдр – справа) является гамильтоновым.
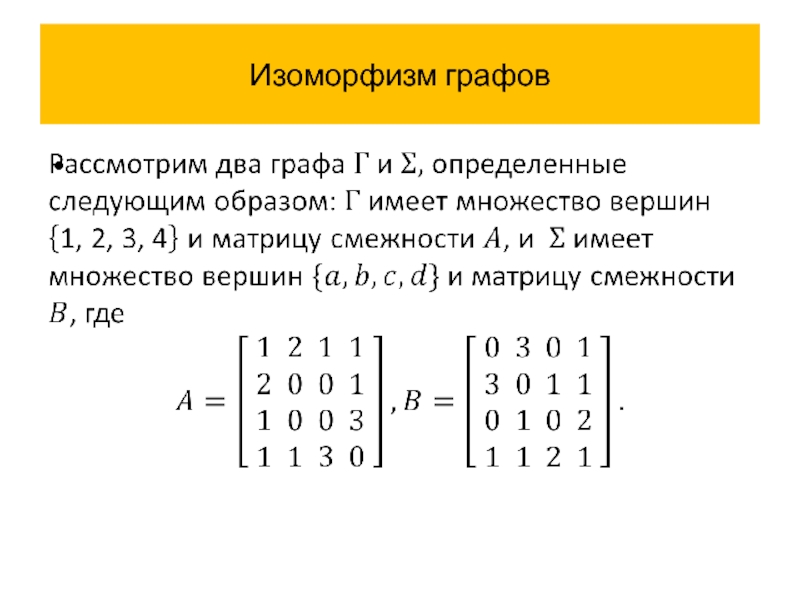
Слайд 49Изоморфизм графов
Так как изоморфные графы имеют, по существу, одно и тоже
строение, то любое теоретико-графовое свойство, которым обладает один граф, должно быть присуще и второму графу.
Мы перечислим некоторые такие свойства в следующей теореме.
Мы перечислим некоторые такие свойства в следующей теореме.
Слайд 60
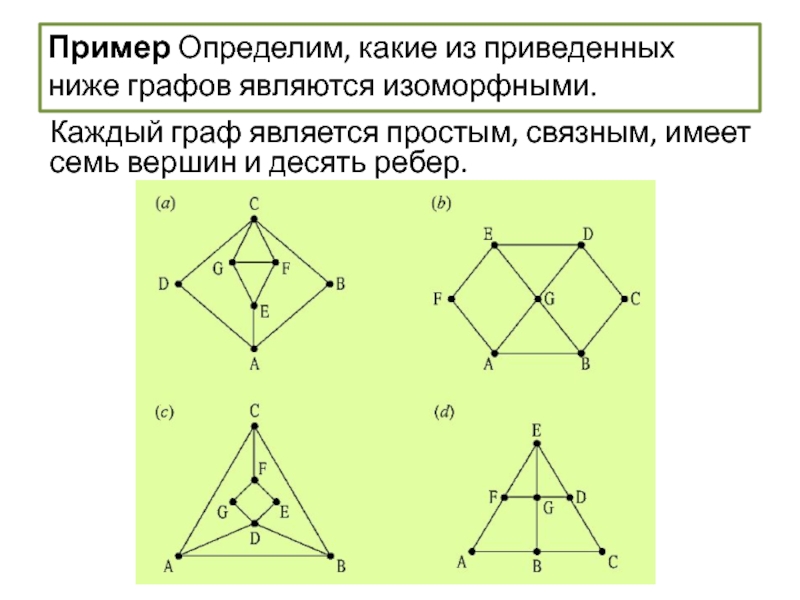
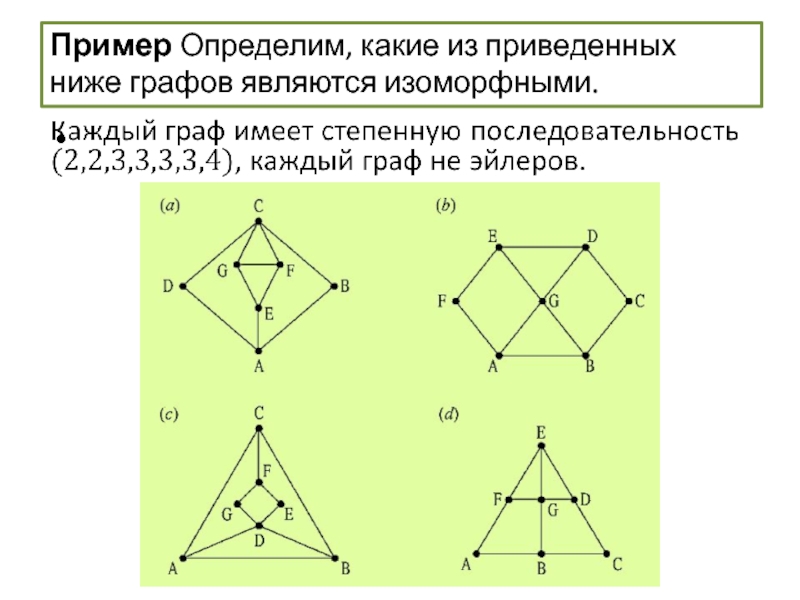
Пример Определим, какие из приведенных ниже графов являются изоморфными.
Каждый граф является
простым, связным, имеет семь вершин и десять ребер.
Слайд 72Изоморфизм графов
Принцип изоморфизма
Чтобы доказать, что два графа изоморфны, следует построить изоморфизм
из одного графа на другой;
чтобы доказать, что два графа неизоморфны, следует найти теоретико-графовое свойство, которым один граф обладает, а второй – нет.
чтобы доказать, что два графа неизоморфны, следует найти теоретико-графовое свойство, которым один граф обладает, а второй – нет.
