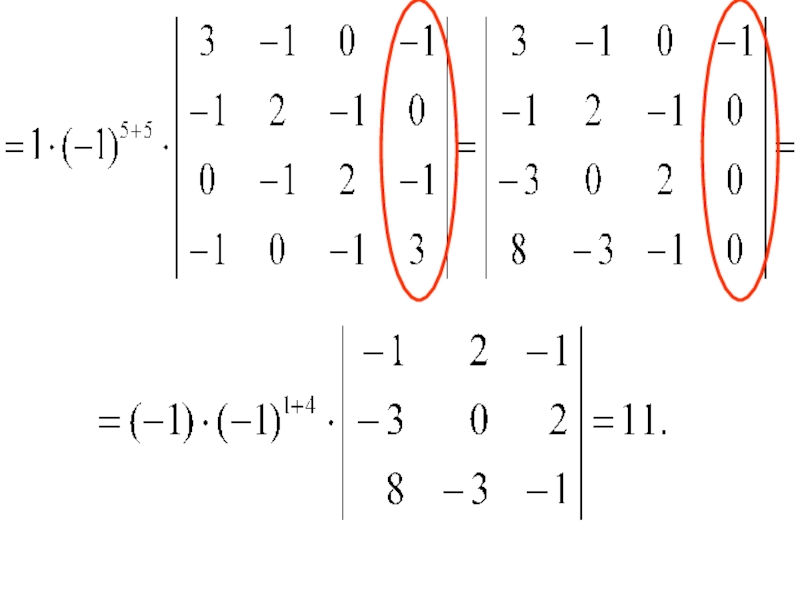- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Деревья. Связность. Дерево и его виды презентация
Содержание
- 1. Деревья. Связность. Дерево и его виды
- 2. Связность. Дерево и его виды Множество
- 3. Например, все компьютеры, включённые в
- 4. В орграфах связность
- 5. Последовательность v1 , е1 , v2 ,
- 6. G1 – дерево Рис. 6 G2
- 7. Следующие утверждения эквивалентны:
- 8. Изобразите все деревья (неизоморфные), которые можно
- 9. Как правило, дерево-граф
- 10. Ориентированным деревом называется орграф без циклов
- 11. Двоичным называется дерево
- 12. Остовы
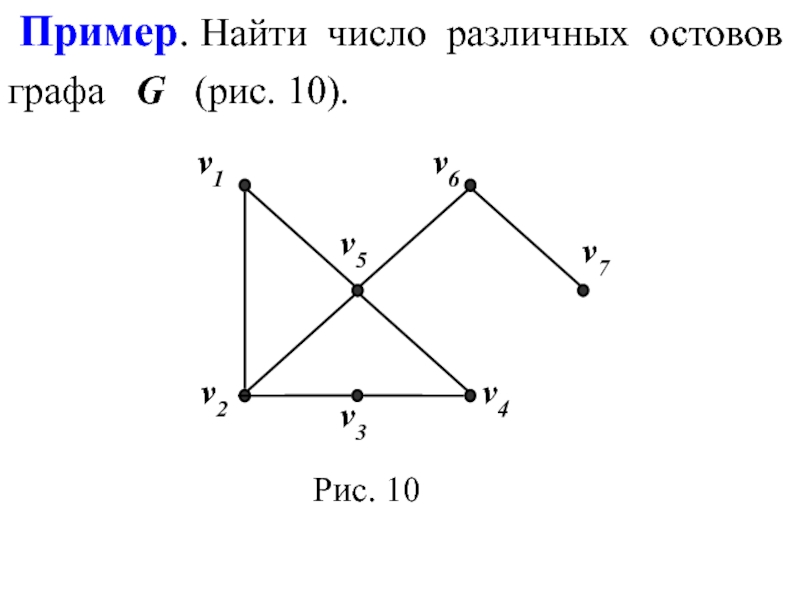
- 13. Пример. Найти число различных остовов графа G (рис. 10).
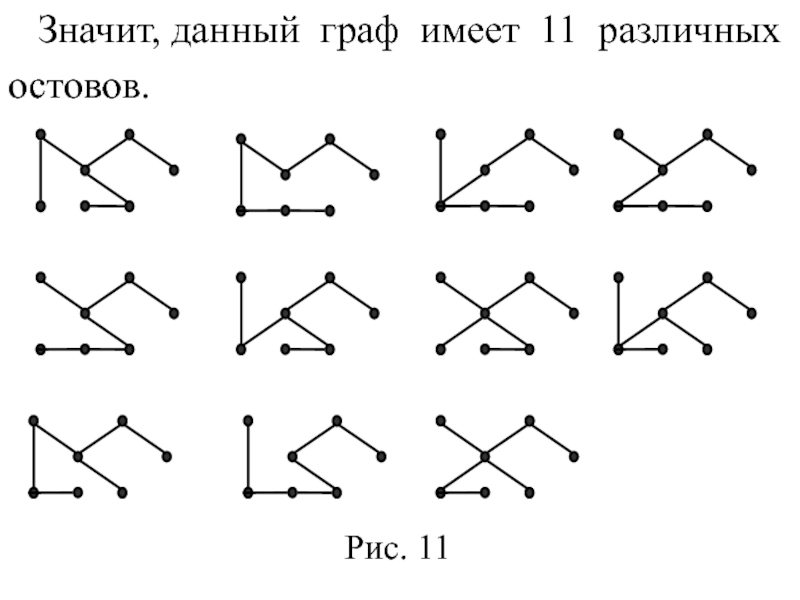
- 19. Значит, данный граф имеет 11 различных остовов. Рис. 11
- 20. Теорема 2. Число
- 21. Алгоритмы нахождения остова минимального
- 22. Другими словами, в задаче
- 23. Шаг 1. Присвоение начальных значений
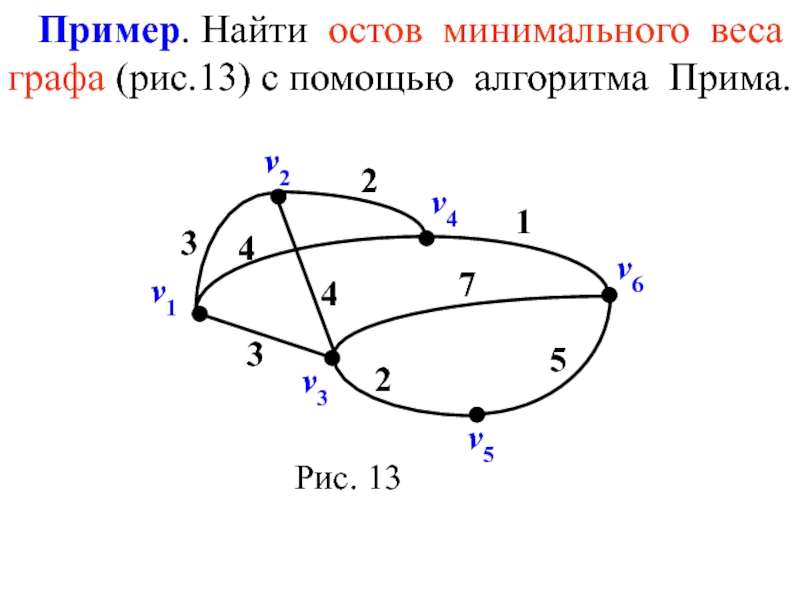
- 24. Пример. Найти остов минимального веса графа (рис.13) с помощью алгоритма Прима. v6
- 25. Шаг 1. Пусть V′ =
- 27. Вторая итерация Шаг 2.
- 29. Третья итерация Шаг 2.
- 31. Четвёртая итерация Шаг 2.
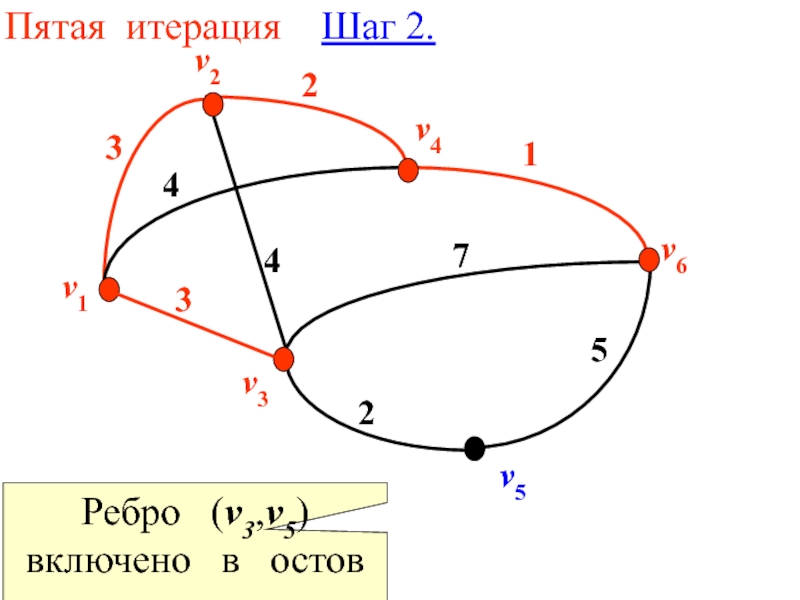
- 33. Пятая итерация Шаг 2.
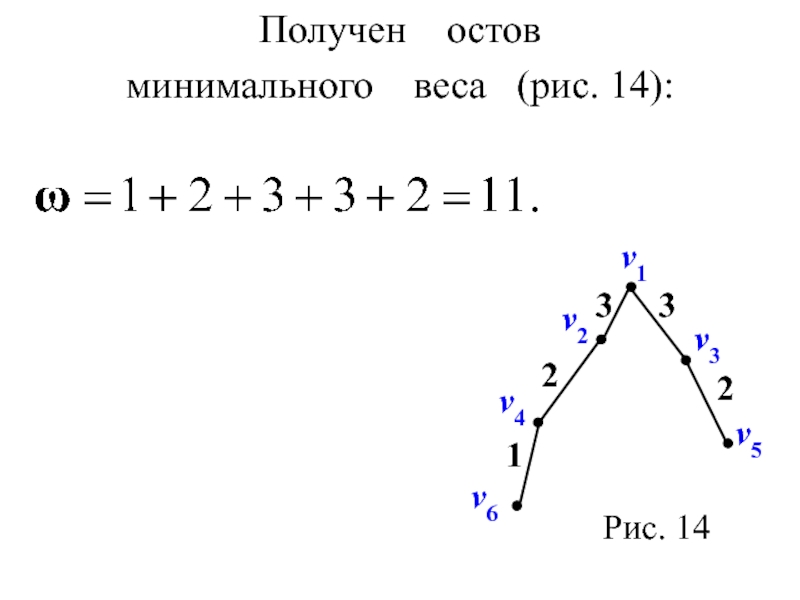
- 35. Получен остов минимального веса
- 36. Алгоритм Краскала Из всех рёбер
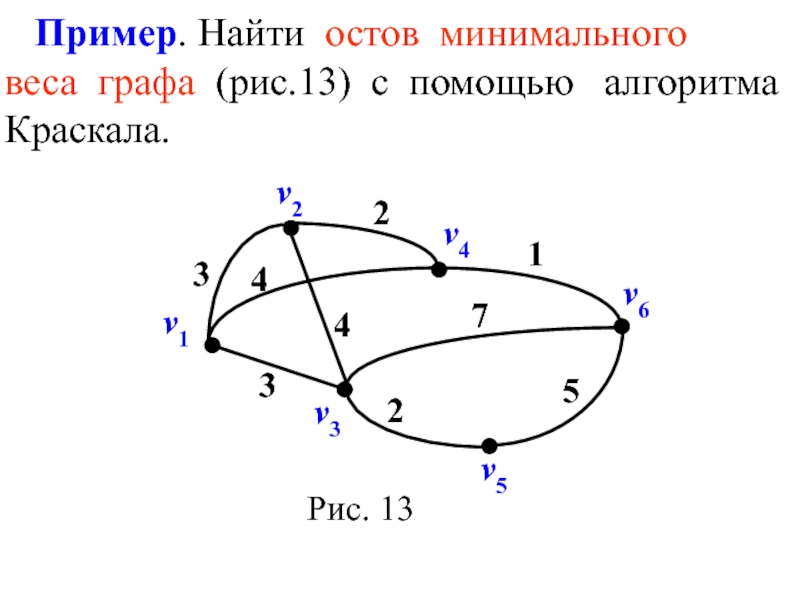
- 37. Пример. Найти остов минимального
- 38. Выбираем ребро с минимальным
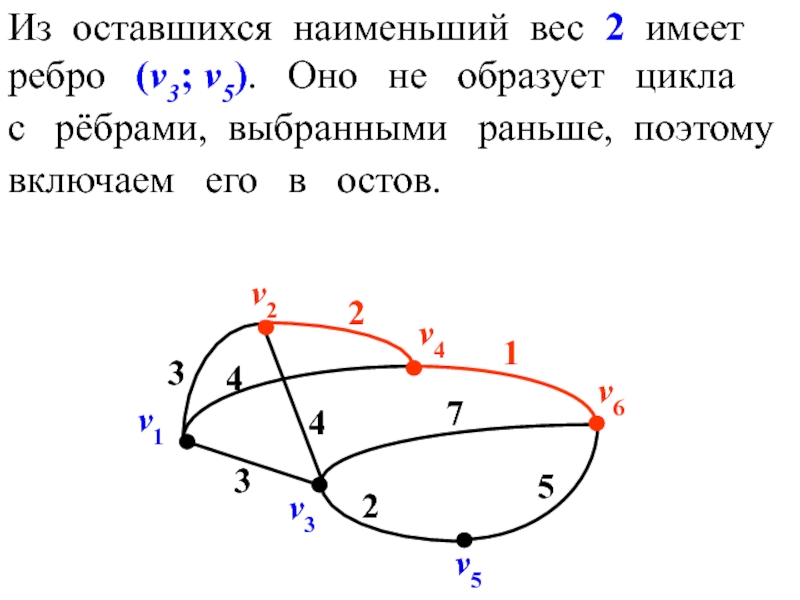
- 39. Из оставшихся наименьший вес 2 имеет ребро
- 40. Следующим ребром, включённым в остов, будет
- 41. Выполнено 5 шагов, поэтому
Слайд 2Связность. Дерево и его виды
Множество вершин графа таких, что любые
из него связаны, а связи с вершинами не из этого
множества нет, называется компонентой
связности графа.
Рис. 1
v1
v2
v3
v4
v5
v6
v7
v8
Рис. 2
v1
v2
v3
v4
v5
v6
v7
Неорграф на рис. 1 имеет
4 компоненты связности:
{v1}, {v2,v3,v4}, {v5,v6,v7}, {v8}.
Орграф на рис. 2 имеет
2 компоненты связности:
{v1, v2, v3}, {v4, v5, v6, v7}.
Граф, содержащий одну компоненту связности,
называется связным.
Слайд 3 Например, все компьютеры, включённые
в Интернет, образуют
Два конкретных компьютера могут быть
не соединёнными напрямую, но от каждого
информацию можно передать на любой
другой.
Связность означает наличие хотя бы
одного пути - последовательности смежных
неповторяющихся рёбер (дуг) между любой
парой вершин графа (графы на рис. 1, 2
несвязные).
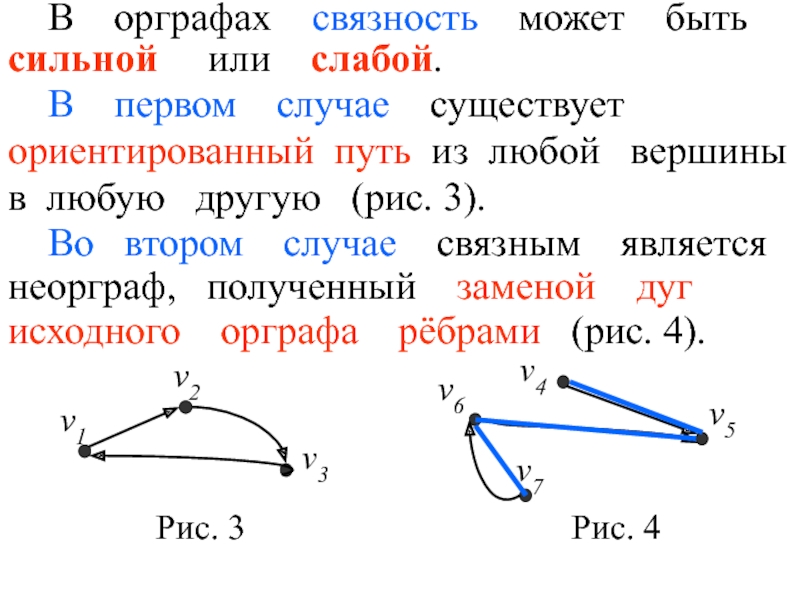
Слайд 4 В орграфах связность может быть
сильной
В первом случае существует
ориентированный путь из любой вершины
в любую другую (рис. 3).
Во втором случае связным является
неорграф, полученный заменой дуг
исходного орграфа рёбрами (рис. 4).
Рис. 3
Рис. 4
v4
v5
v6
v7
v1
v2
v3
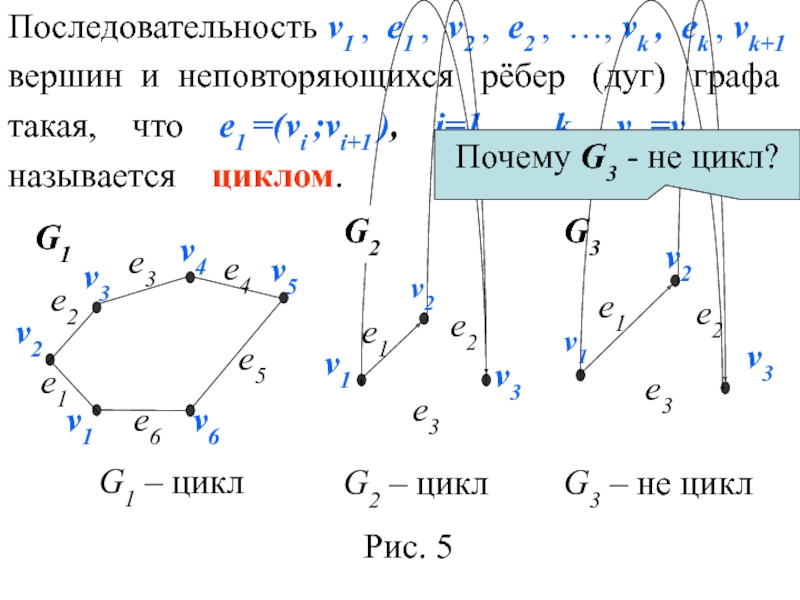
Слайд 5Последовательность v1 , е1 , v2 , е2 , …, vk
вершин и неповторяющихся рёбер (дуг) графа
такая, что е1 =(vi ;vi+1 ), i=1, …, k, v1 =vk+1
называется циклом.
Рис. 5
v2
Почему G3 - не цикл?
Слайд 6
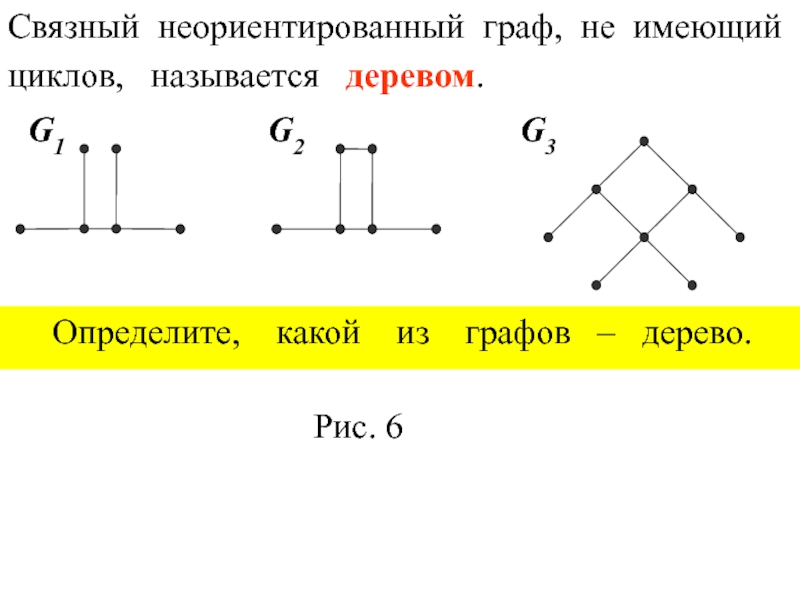
G1 – дерево
Рис. 6
G2 – не дерево
G3 – не дерево
Связный неориентированный
циклов, называется деревом.
Определите, какой из графов – дерево.
Слайд 7 Следующие утверждения эквивалентны:
G – дерево.
G
ребер m на единицу меньше числа вершин n:
m = n - 1.
3. Любые две вершины дерева соединяет
единственный путь.
G – неорграф без циклов и если любую
пару несмежных вершин соединить ребром,
то G будет содержать единственный цикл.
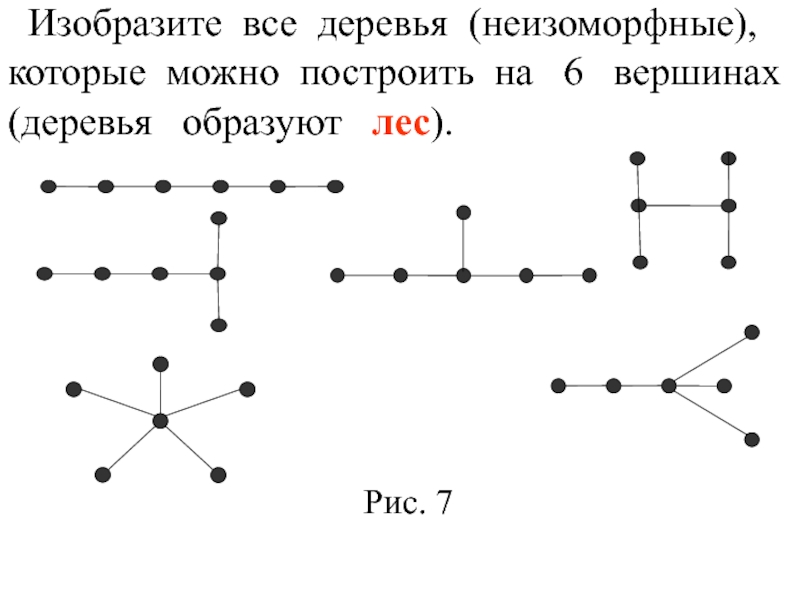
Слайд 8 Изобразите все деревья (неизоморфные),
которые можно построить на 6
(деревья образуют лес).
Рис. 7
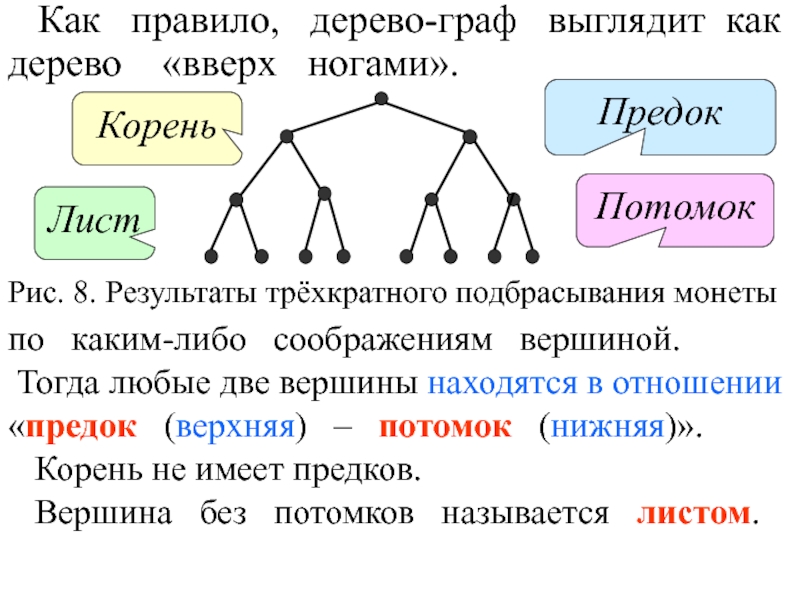
Слайд 9 Как правило, дерево-граф выглядит как
дерево
Корневым называется дерево с выделенной
по каким-либо соображениям вершиной.
Тогда любые две вершины находятся в отношении
«предок (верхняя) – потомок (нижняя)».
Корень не имеет предков.
Вершина без потомков называется листом.
Рис. 8. Результаты трёхкратного подбрасывания монеты
Корень
Лист
Предок
Потомок
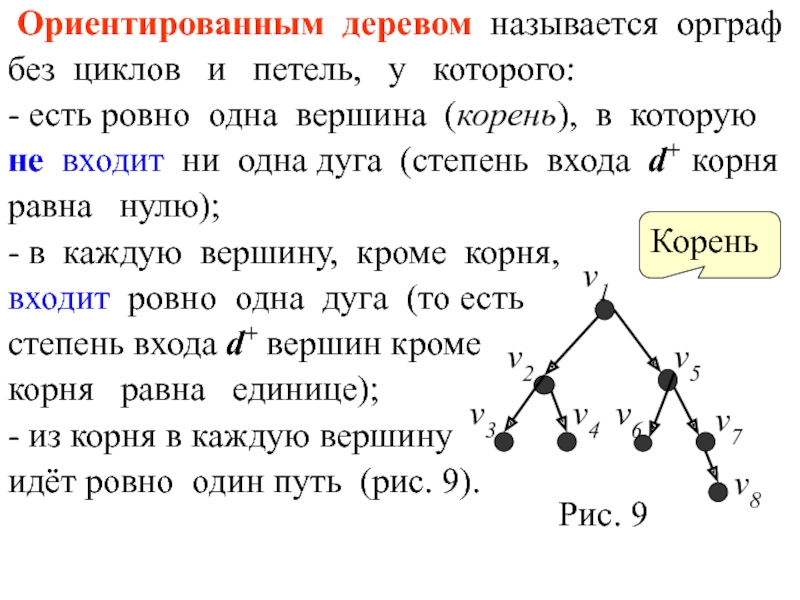
Слайд 10 Ориентированным деревом называется орграф
без циклов и петель,
- есть ровно одна вершина (корень), в которую
не входит ни одна дуга (степень входа d+ корня
равна нулю);
- в каждую вершину, кроме корня,
входит ровно одна дуга (то есть
степень входа d+ вершин кроме
корня равна единице);
- из корня в каждую вершину
идёт ровно один путь (рис. 9).
Рис. 9
v1
v2
v3
v4
v5
v6
v7
v8
Корень
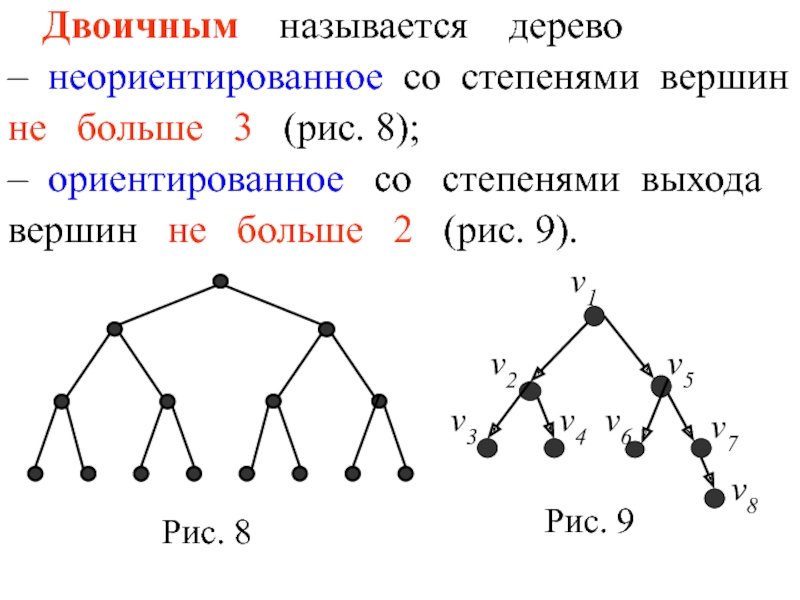
Слайд 11 Двоичным называется дерево
– неориентированное со степенями вершин
не
– ориентированное со степенями выхода
вершин не больше 2 (рис. 9).
Слайд 12Остовы
Граф G′ называется подграфом графа G,
если
а множество рёбер G′ образовано
некоторыми рёбрами G .
Остовным деревом (каркасом, остовом) графа G называется его связный без циклов
подграф G′.
Теорема 1 (Кирхгофа). Число различных
остовов связного графа G с n вершинами
(n ≥ 2) равно алгебраическому дополнению любого элемента матрицы Кирхгофа K(G), состоящей из элементов
Слайд 20 Теорема 2. Число рёбер неорграфа G,
которые
остова, не зависит от порядка их удаления
и равно ν(G) = m – n + k, где m – число рёбер,
n – число вершин, k – число компонент
cвязности графа G.
ν (G) = m – n + k = m - (n - k)
Ясно, что ν′(G) + ν(G) = m .
Для графа на рис. 12
ν (G) = 9 – 7 + 2 = 4,
ν′(G) = 7 – 2 = 5.
Рис. 12
Цикломатическое число графа G
n – k = ν′(G) - коранг графа G
Слайд 21Алгоритмы нахождения остова минимального веса
Связный граф может
Часто остов требуется выбрать
из оптимальных соображений: его
минимального или максимального веса.
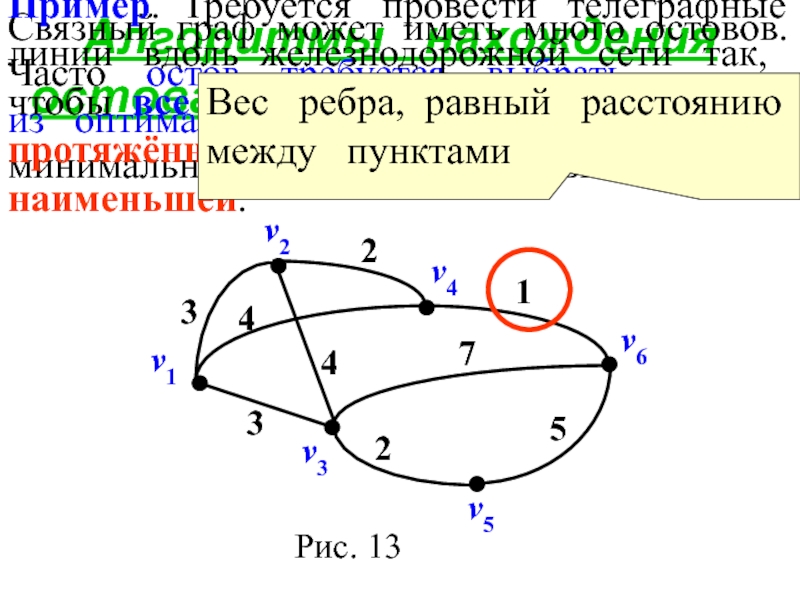
Пример. Требуется провести телеграфные линии вдоль железнодорожной сети так, чтобы все пункты были связаны, а общая
протяжённость линий была наименьшей.
v6
1
3
5
7
v2
v4
v1
v3
v5
3
2
4
4
2
Рис. 13
Вес ребра, равный расстоянию
между пунктами
Слайд 22 Другими словами, в задаче нужно
найти остов
Алгоритм Прима
Разобьём множество вершин V на два
подмножества V′ и V′′ таких, что ,
, , Ø.
Число
называется пошаговым расстоянием
между V′ и V′′ .
Слайд 23Шаг 1. Присвоение начальных значений
Пусть
, Ø.
Шаг 2. Обновление данных
Найдём ребро (vi;vj) такое, что , ,
.
Полагаем , ,
.
Шаг 3. Проверка на завершение
Если V′ = V, то G′ =( V′, U′ ) – искомый остов.
Иначе - переход к шагу 2.
Слайд 25Шаг 1. Пусть V′ = {v1}, тогда
U′ = Ø.
Первая итерация
Шаг 2. .
Включим, например, вершину v2 в V′ :
, тогда
Шаг 3. V′ ≠ V, переход к шагу 2.
Из трёх рёбер, инцидентных вершине v1, наименьший вес имеют два.
Слайд 26
v6
1
3
5
7
v4
v1
v3
v5
3
2
4
4
2
v2
Шаг 1.
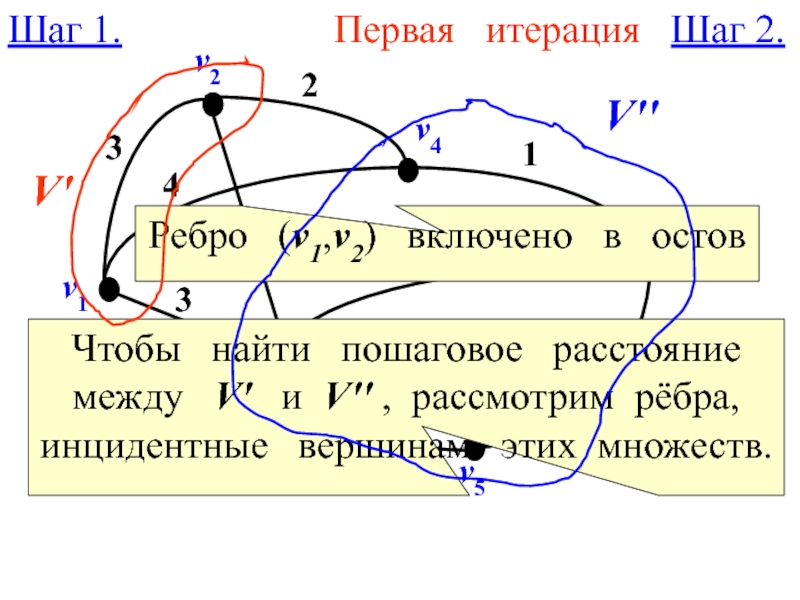
Первая итерация Шаг 2.
Ребро (v1,v2)
Чтобы найти пошаговое расстояние
между V′ и V′′ , рассмотрим рёбра, инцидентные вершинам этих множеств.
V′
V′′
Слайд 28
v6
1
3
5
7
v4
v1
v3
v5
3
2
4
4
2
v2
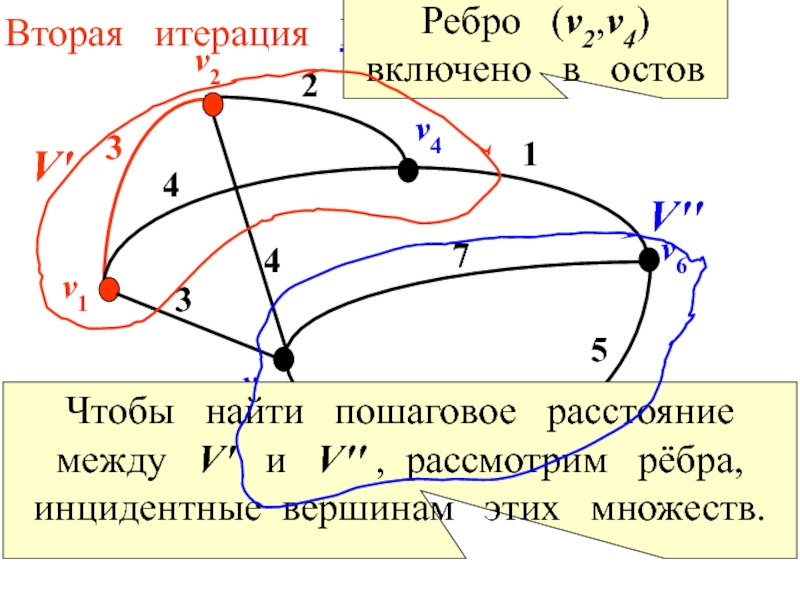
Вторая итерация Шаг 2.
Ребро (v2,v4)
Чтобы найти пошаговое расстояние
между V′ и V′′ , рассмотрим рёбра, инцидентные вершинам этих множеств.
V′
V′′
Слайд 30
v6
1
3
5
7
v4
v1
v3
v5
3
2
4
4
2
v2
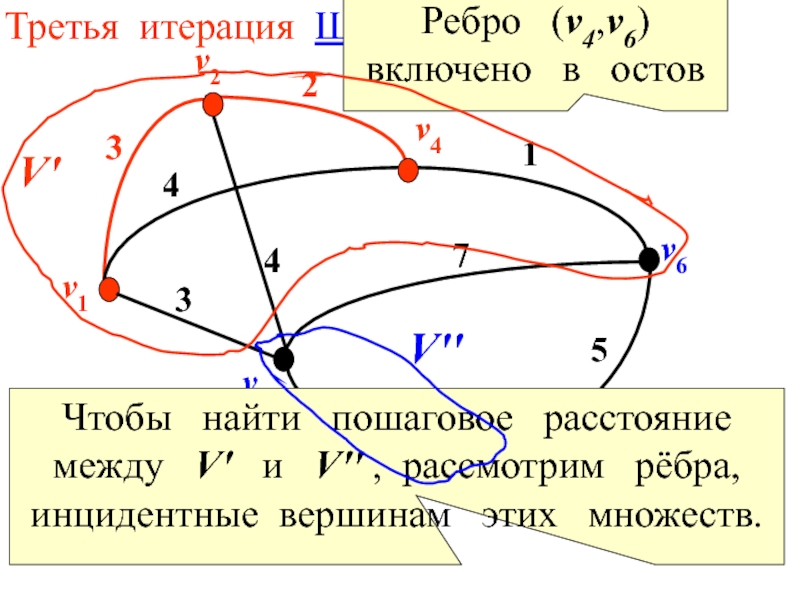
Третья итерация Шаг 2.
Ребро (v4,v6) включено
Чтобы найти пошаговое расстояние
между V′ и V′′ , рассмотрим рёбра, инцидентные вершинам этих множеств.
V′
V′′
Слайд 32
v6
1
3
5
7
v4
v1
v3
v5
3
2
4
4
2
v2
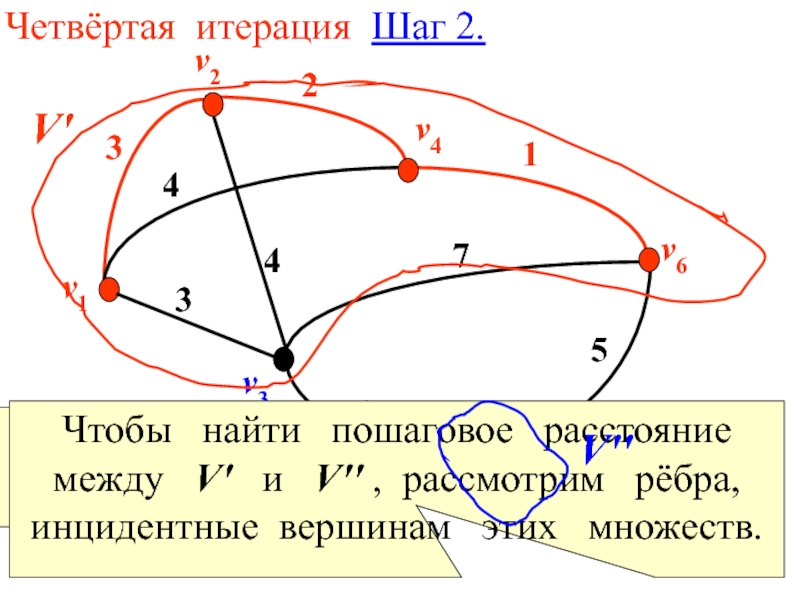
Четвёртая итерация Шаг 2.
Ребро (v1,v3) включено
Чтобы найти пошаговое расстояние
между V′ и V′′ , рассмотрим рёбра, инцидентные вершинам этих множеств.
V′
V′′
Слайд 36 Алгоритм Краскала
Из всех рёбер выбирают одно с наименьшим
весом. Затем
с наименьшим весом. Если оно не образует
цикла с выбранными ранее рёбрами, то
вводится в остов. Построение прекращается
после n-1 шагов (n – число вершин).
Слайд 38 Выбираем ребро с минимальным весом:
(v4; v6) c
Снова выбираем ребро с минимальным
весом, не образующее цикла с ребром,
выбранным ранее: ребро (v2; v4) c весом 2.
Включаем его в строящийся остов.
v6
1
3
5
7
v2
v4
v1
v3
v5
3
2
4
4
2
Слайд 39Из оставшихся наименьший вес 2 имеет
ребро (v3; v5). Оно
с рёбрами, выбранными раньше, поэтому
включаем его в остов.
v6
1
3
5
7
v2
v4
v1
v3
v5
3
2
4
4
2
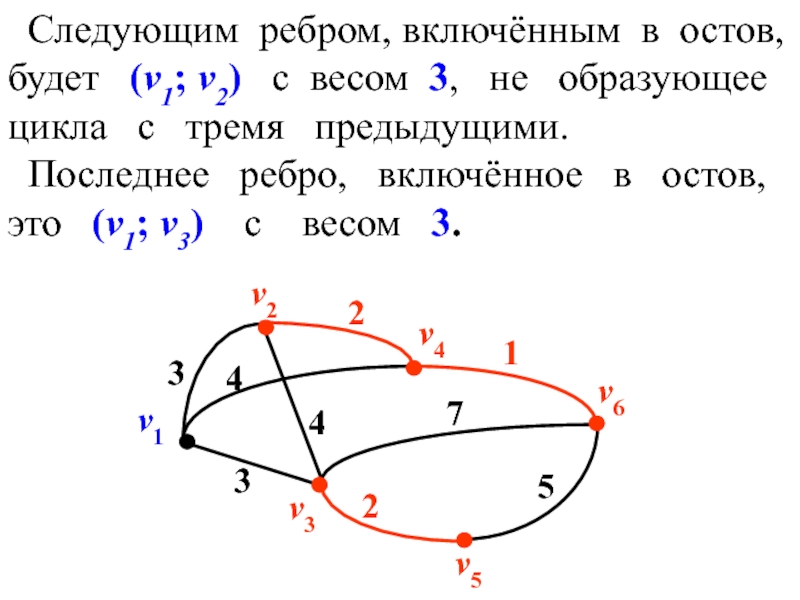
Слайд 40 Следующим ребром, включённым в остов,
будет (v1; v2) с
цикла с тремя предыдущими.
Последнее ребро, включённое в остов,
это (v1; v3) с весом 3.
v6
1
3
5
7
v2
v4
v1
v3
v5
3
2
4
4
2