параметров распределения
Точечные и интервальные оценки
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистические оценки параметров распределения. Точечные и интервальные оценки (Лекция 9) презентация
Содержание
- 2. Теория вероятностей УГТУ-УПИ 2008г. М.А.Вигура, О.А.Кеда, А.Ф.Рыбалко,
- 3. Цель лекции: 1. Овладеть соответствующим математическим
- 4. Формируемые компетенции по ФГОС:
- 5. Лекция 9 Статистические оценки параметров распределения Точечные и интервальные оценки
- 6. При изучении случайной величины X, распределенной в
- 10. оценки параметров распределения Точечная оценка неизвестного параметра Интервальная оценка неизвестного параметра
- 11. Несмещенные, состоятельные и эффективные оценки Для
- 12. Оценки
- 13. Несмещенные, состоятельные и эффективные оценки З.
- 14. Точечная оценка генерального среднего по выборочному среднему
- 15. Точечная оценка генерального среднего по выборочному среднему
- 16. Точечная оценка генеральной дисперсии по исправленной выборочной
- 17. Точечная оценка генеральной дисперсии по исправленной выборочной
- 18. Интервальные оценки
- 19. Графический смысл
- 20. Интервальные оценки
- 21. Точечные оценки проще в вычислении, но не
- 22. Интервальные оценки
- 23. для получения интервальной оценки Как
- 24. Приближенный способ состоит в замене неизвестных
- 25. Точный способ может быть использован лишь
- 26. С интервальной оценкой связано решение трех типов
- 27. Интервальная оценка математического ожидания нормально распределенной случайной
- 28. Интервальная оценка математического ожидания нормально распределенной случайной
- 29. 1) Определим, с какой надежностью математическое ожидание
- 30. 2) По выборочному значению математического ожидания
- 31. 3) По заданным σ, ε и γ,
- 32. Пример: 1:
- 33. Пример: 2:
- 34. Пример: 3:
- 35. Доверительный интервал для оценки неизвестного математического ожидания
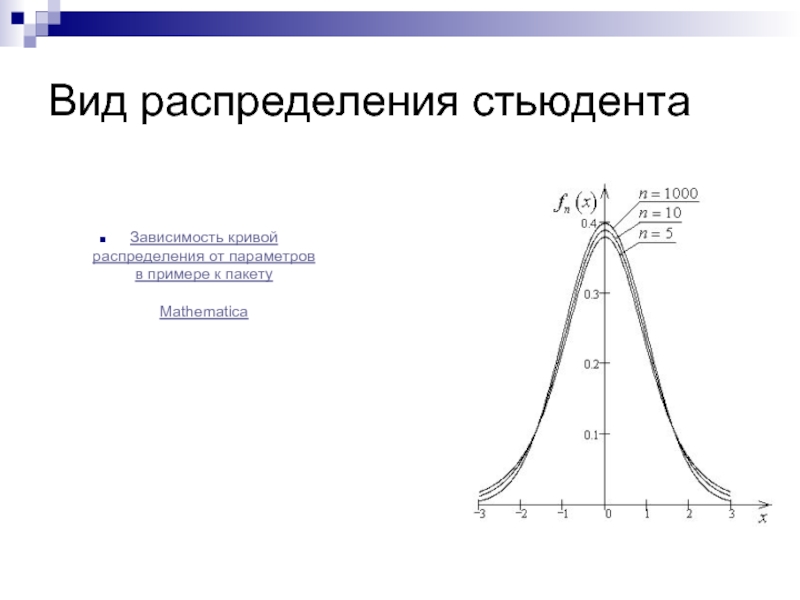
- 38. Вид распределения стьюдента Зависимость кривой распределения от параметров в примере к пакету Mathematica
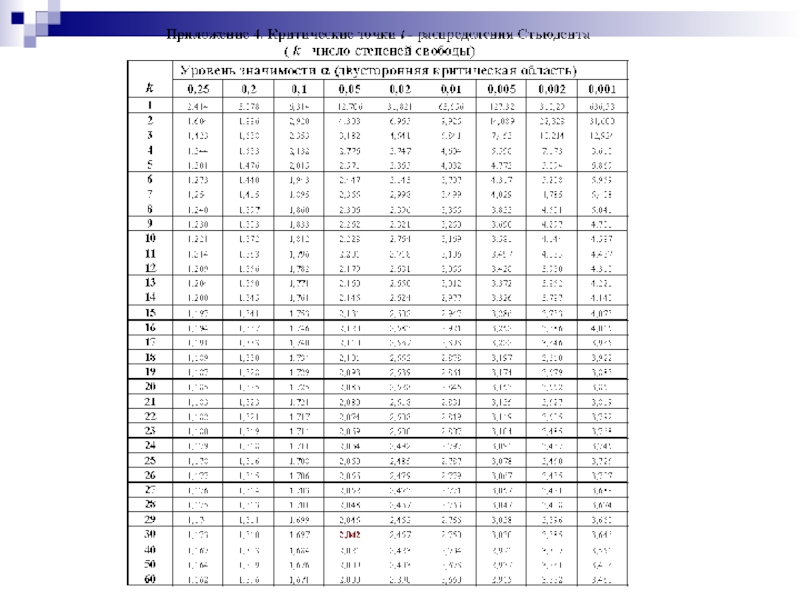
- 39. Распределение стьюдента
- 41. Пример: 3:
- 42. В результате студент должен уметь: по
- 43. Перечень источников, список дополнительной литературы по
Теория вероятностей УГТУ-УПИ 2008г. М.А.Вигура, О.А.Кеда, А.Ф.Рыбалко, Н.М.Рыбалко, А.Б.Соболев Лекция 9 Статистические оценки параметров распределения
Точечные и интервальные оценки
Слайд 2Теория вероятностей
УГТУ-УПИ
2008г.
М.А.Вигура, О.А.Кеда, А.Ф.Рыбалко,
Н.М.Рыбалко, А.Б.Соболев
Лекция 9
Статистические оценки
Слайд 3
Цель лекции:
1. Овладеть соответствующим математическим аппаратом для дальнейшего изучения курса математики,
демонстрировать и использовать математические методы в ходе изучения специальных дисциплин для будущей профессиональной деятельности.
2. Научиться по данным выборки получать точечные и интервальные оценки параметров распределения при построении математических моделей случайных событий , в том числе и с использованием предельных теорем теории вероятностей.
Слайд 6При изучении случайной величины X, распределенной в генеральной совокупности, часто из
теоретических соображений удается установить вид распределения и по данным выборки необходимо оценить (приближенно найти) его численные параметры.
Например, если случайная величина имеет нормальное распределение, то для полного его определения необходимо оценить его математическое ожидание и среднее квадратическое отклонение.
Например, если случайная величина имеет нормальное распределение, то для полного его определения необходимо оценить его математическое ожидание и среднее квадратическое отклонение.
Слайд 10оценки параметров распределения
Точечная оценка неизвестного параметра
Интервальная оценка неизвестного параметра
Слайд 11Несмещенные, состоятельные и эффективные оценки
Для того, чтобы статистической оценке можно
было доверять, она должна обладать некоторыми свойствами.
Точечные оценки
Слайд 13Несмещенные, состоятельные и эффективные оценки
З. На практике не всегда удается
добиться выполнения всех трех требований к оценке. Соображения практической удобности заставляют пользоваться не полностью адекватными оценками, но необходимо представлять, каким свойством мы пренебрегаем. Ниже, при рассмотрении конкретных оценок, эти аспекты будут обсуждаться.
Слайд 16Точечная оценка генеральной дисперсии по исправленной выборочной дисперсии
Можно показать, что
выборочная дисперсия (среднее значение квадрата отклонения) является смещенной оценкой генеральной дисперсии.
Слайд 17Точечная оценка генеральной дисперсии по исправленной выборочной дисперсии
Для получения несмещенной
оценки достаточно перейти к исправленной выборочной дисперсии
Слайд 21Точечные оценки проще в вычислении, но не позволяют установить степень достоверности
оценки.
Интегральные оценки, наряду с возможными границами значений параметра, дают вероятность, с которой истинное значение параметра лежит между этими (случайными) границами.
Естественно, чем больше надежность оценки, тем шире доверительный интервал, и наоборот, так что практические вычисления являются компромиссом между точностью и надежностью оценки. Наиболее часто задают надежность 0,95; 0,99 и 0,999.
Интегральные оценки, наряду с возможными границами значений параметра, дают вероятность, с которой истинное значение параметра лежит между этими (случайными) границами.
Естественно, чем больше надежность оценки, тем шире доверительный интервал, и наоборот, так что практические вычисления являются компромиссом между точностью и надежностью оценки. Наиболее часто задают надежность 0,95; 0,99 и 0,999.
Слайд 23
для получения интервальной оценки
Как правило вид генерального распределения постулируется(нормальное распределение,
равномерное распределение и т.д.). При достаточно большом объеме выборки реальную функцию распределения оценки с достаточной точностью можно заменить асимптотической
Значения параметров генерального распределения оценивают либо приближенно либо точно.
Слайд 24Приближенный способ
состоит в замене неизвестных параметров генеральной совокупности, от которых
зависит распределение , на их точечные оценки, полученные в результате выборки.
Далее оценка строится, как если бы параметры распределения были бы известны.
Далее оценка строится, как если бы параметры распределения были бы известны.
Слайд 25Точный способ
может быть использован лишь в том случае, когда известен
закон генерального распределения. При этом строятся вспомогательные случайные величины, распределение которых зависит лишь от объема выборки.
В частности, при оценке среднего значения нормально распределенной генеральной совокупности можно использовать оценку
которая подчиняется распределению Стьюдента, зависящему только от объема выборки .
В частности, при оценке среднего значения нормально распределенной генеральной совокупности можно использовать оценку
которая подчиняется распределению Стьюдента, зависящему только от объема выборки .
Слайд 26С интервальной оценкой связано решение трех типов задач
1) определение доверительной
вероятности по заданному доверительному интервалу и объему выборки;
2) определение доверительного интервала по заданной доверительной вероятности и объему выборки;
3) определение необходимого объема выборки по заданным доверительной вероятности и доверительному интервалу
Слайд 27Интервальная оценка математического ожидания нормально распределенной случайной величины при известном σ
Слайд 28Интервальная оценка математического ожидания нормально распределенной случайной величины при известном σ
Слайд 291) Определим, с какой надежностью математическое ожидание а покрывается доверительным интервалом
при заданной точности ε, т.е. найдем
Слайд 302) По выборочному значению математического ожидания и
известному σ найти доверительный интервал, который с заданной надежностью γ покрывает математическое ожидание а генеральной совокупности. Это и есть задача получения интервальной оценки
Слайд 35Доверительный интервал для оценки неизвестного математического ожидания нормально распределенной случайной величины
при неизвестном σ.
Слайд 38Вид распределения стьюдента
Зависимость кривой распределения от параметров в примере к пакету
Mathematica
Слайд 42В результате студент должен уметь:
по данным выборки получать точечные и интервальные
оценки
параметров распределения при построении математических
моделей случайных событий , в том числе и с использованием
предельных теорем теории вероятностей.
Слайд 43Перечень источников,
список дополнительной литературы по теме.
Сборник задач по математике: Учеб.
пособие для втузов : В 4 ч. Ч. 4: Теория вероятностей. Математическая статистика / Э. А. Вуколов, А. В. Ефимов, В. Н. Земсков, А. С. Поспелов; Под общ. ред. А. В. Ефимова, А. С. Поспелова. - 3-е изд., перераб. и доп. - М.: Физматлит, 2004. - 432 с.: ил.; 21 см. - Библиогр.: с. 431 (16 назв.). - ISBN 5-94052-037-5.
Чудесенко, Валерий Федорович. Сборник заданий по специальным курсам высшей математики (типовые расчеты): Учеб. пособие для вузов / В. Ф. Чудесенко. - 2-е изд., перераб. - М.: Высшая школа, 1999. - 126 с. - ISBN 5-06-003065-2.
Гмурман, Владимир Ефимович. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для вузов. - 5-е изд., стер. - М.: Высш. шк., 1999. - 400 с. - ISBN 5-06-003465-8.
Вентцель, Елена Сергеевна. Задачи и упражнения по теории вероятностей: учеб. пособие для студентов втузов / Е. С. Вентцель, Л. А. Овчаров. - 5-е изд., испр. - М.: Академия, 2004. - 448 с.: ил.; 21 см. - (Высшее образование). - Библиогр.: с. 240 (12 назв.). - ISBN 5-7695-1054-4.
Агапов, Георгий Иванович. Задачник по теории вероятностей: Учеб. пособие для втузов. - 2-е изд., доп. - М.: Высш.шк., 1994. - 112с. - ISBN 5-06-002664-7.
Чудесенко, Валерий Федорович. Сборник заданий по специальным курсам высшей математики (типовые расчеты): Учеб. пособие для вузов / В. Ф. Чудесенко. - 2-е изд., перераб. - М.: Высшая школа, 1999. - 126 с. - ISBN 5-06-003065-2.
Гмурман, Владимир Ефимович. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для вузов. - 5-е изд., стер. - М.: Высш. шк., 1999. - 400 с. - ISBN 5-06-003465-8.
Вентцель, Елена Сергеевна. Задачи и упражнения по теории вероятностей: учеб. пособие для студентов втузов / Е. С. Вентцель, Л. А. Овчаров. - 5-е изд., испр. - М.: Академия, 2004. - 448 с.: ил.; 21 см. - (Высшее образование). - Библиогр.: с. 240 (12 назв.). - ISBN 5-7695-1054-4.
Агапов, Георгий Иванович. Задачник по теории вероятностей: Учеб. пособие для втузов. - 2-е изд., доп. - М.: Высш.шк., 1994. - 112с. - ISBN 5-06-002664-7.
