- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие вектора презентация
Содержание
- 1. Понятие вектора
- 2. Длиной или модулем вектора называется длина отрезка
- 3. Любая точка плоскости также
- 4. Назовите векторы, изображенные на
- 5. Многие физические величины,
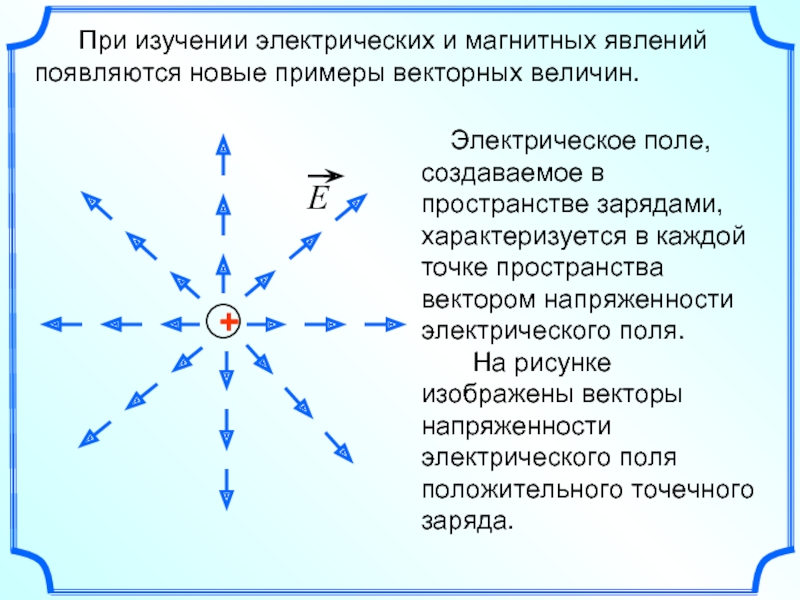
- 6. При изучении электрических и магнитных явлений появляются новые примеры векторных величин.
- 7. Электрический ток, т.е. направленное
- 8. Два ненулевых вектора
- 9. Два ненулевых вектора
- 10. Векторы называются равными,
- 11. Если точка А –
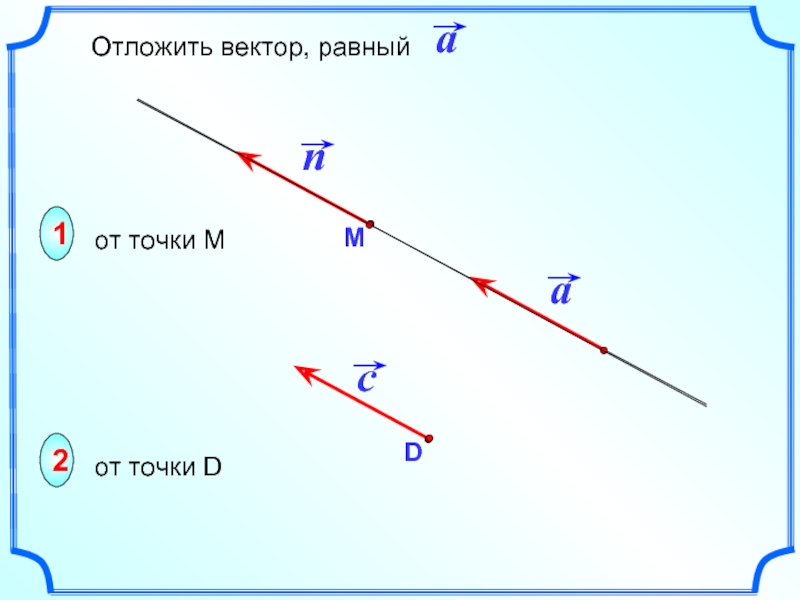
- 12. 1 2 от точки М от точки D
- 13. С А В
- 14. № 747 Укажите
- 16. № 747 Укажите
- 17. № 747 Укажите
- 18. № 748 В
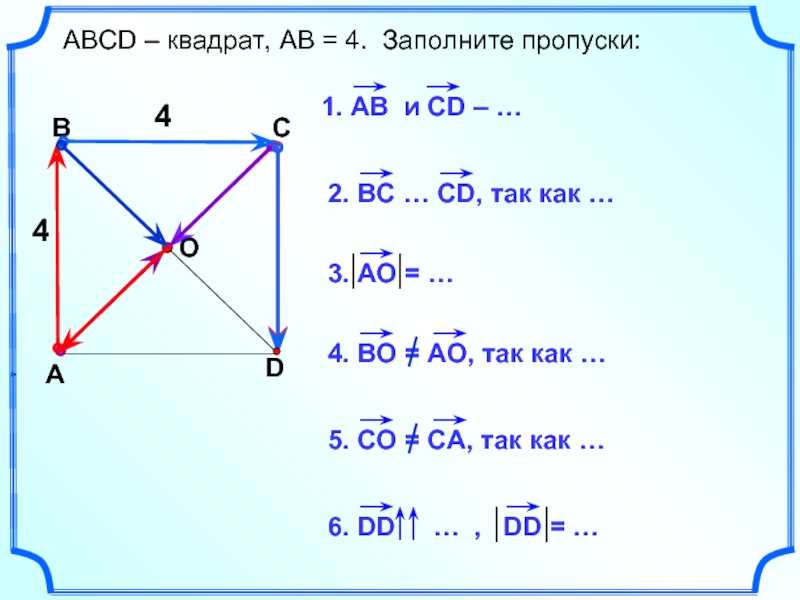
- 19. АВСD –
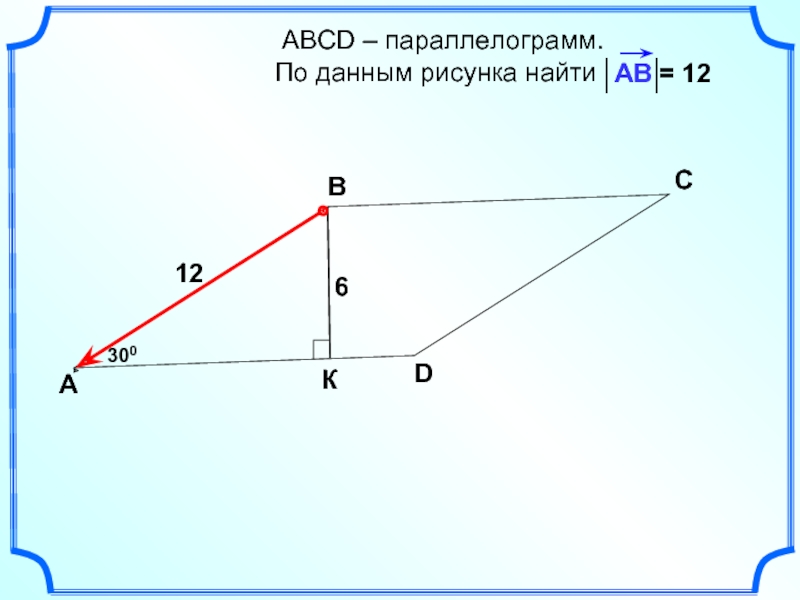
- 20. АВСD – параллелограмм.
- 21. АВС – равнобедренный треугольник.
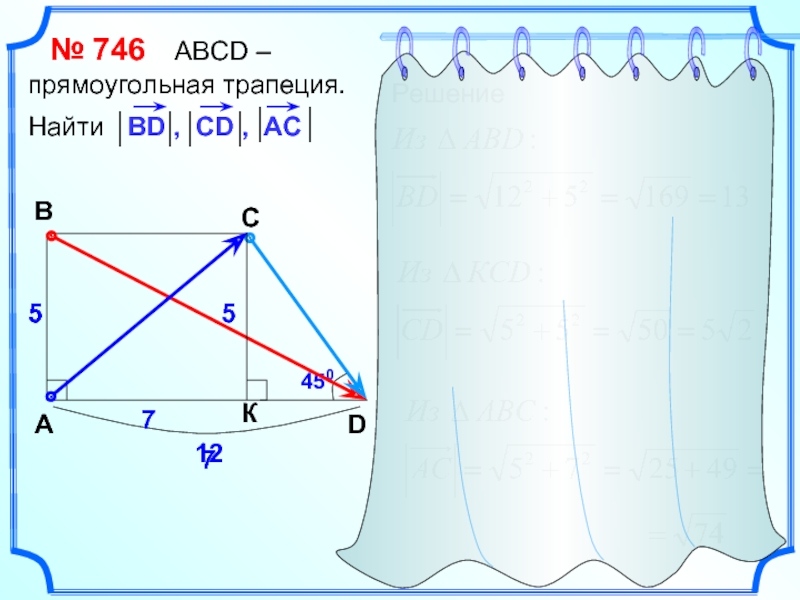
- 22. № 746 АВСD
- 23. № 749 Точки
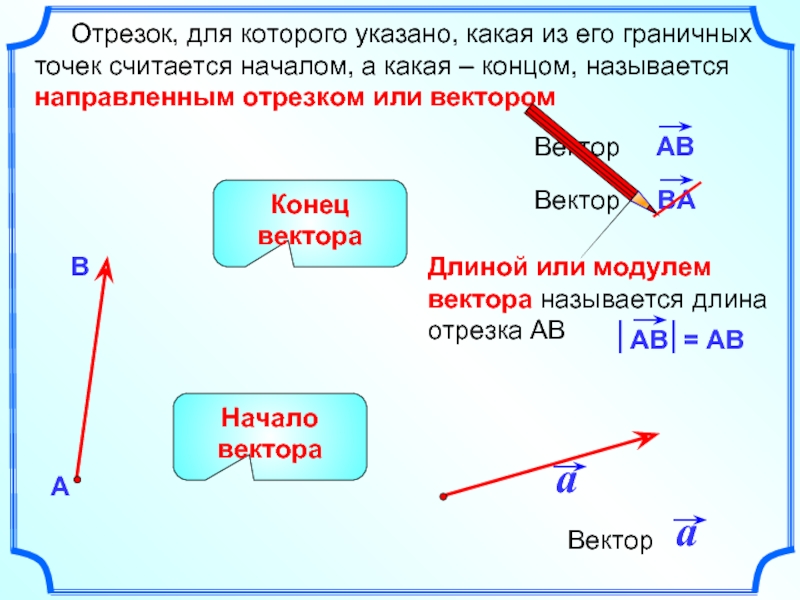
Слайд 2Длиной или модулем вектора называется длина отрезка АВ
Отрезок,
Начало вектора
Конец вектора
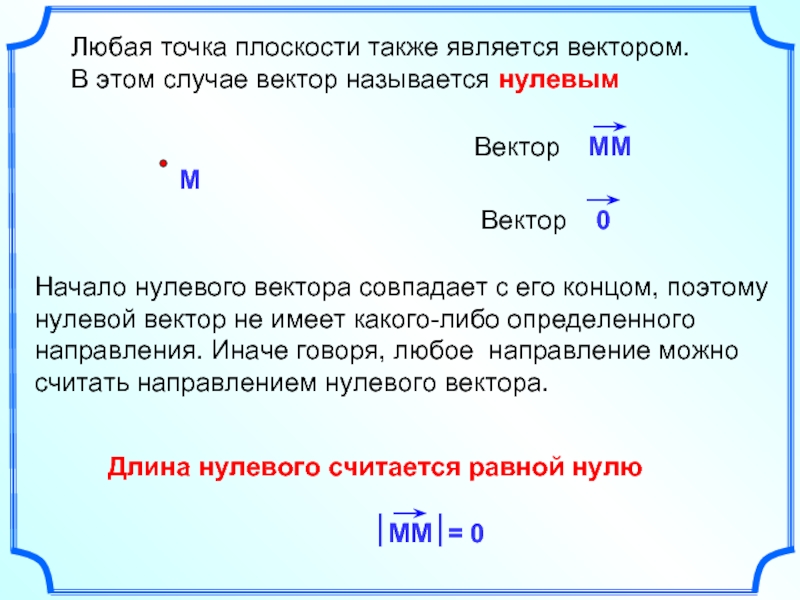
Слайд 3 Любая точка плоскости также является вектором.
Длина нулевого считается равной нулю
Начало нулевого вектора совпадает с его концом, поэтому нулевой вектор не имеет какого-либо определенного направления. Иначе говоря, любое направление можно считать направлением нулевого вектора.
Слайд 5
Многие физические величины, например
сила, перемещение материальной
8 Н
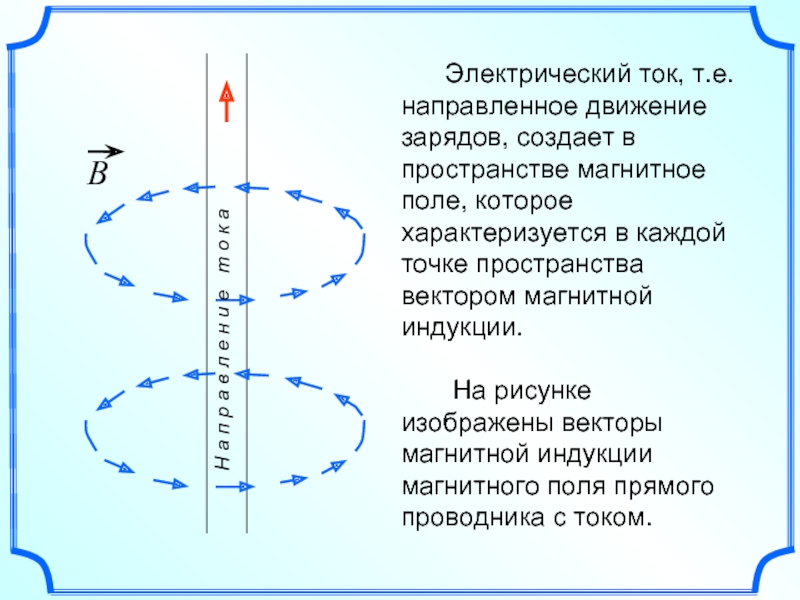
Слайд 7 Электрический ток, т.е. направленное движение зарядов, создает в
На рисунке изображены векторы магнитной индукции магнитного поля прямого проводника с током.
Слайд 8
Два ненулевых вектора называются коллинеарными, если они лежат на
Коллинеарные, сонаправленные векторы
Нулевой вектор считается коллинеарным, сонаправленным с любым вектором.
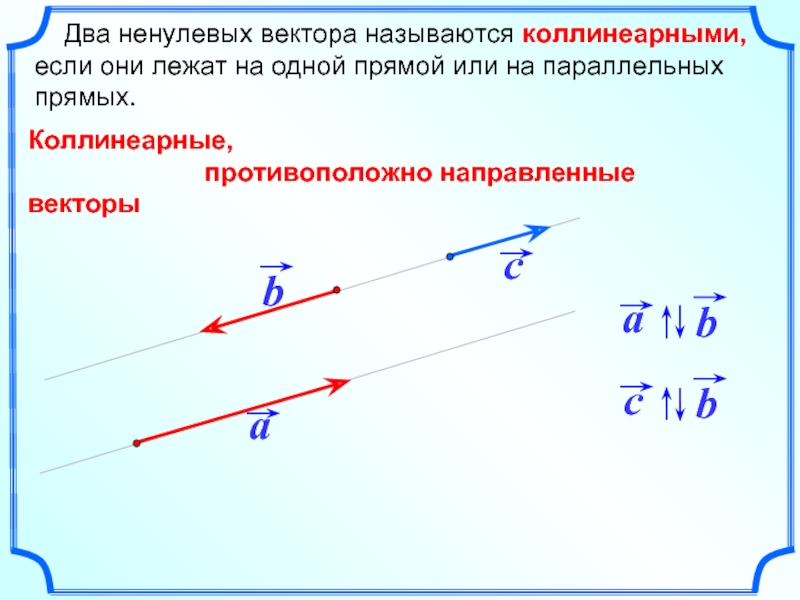
Слайд 9
Два ненулевых вектора называются коллинеарными, если они лежат на
Коллинеарные,
противоположно направленные векторы
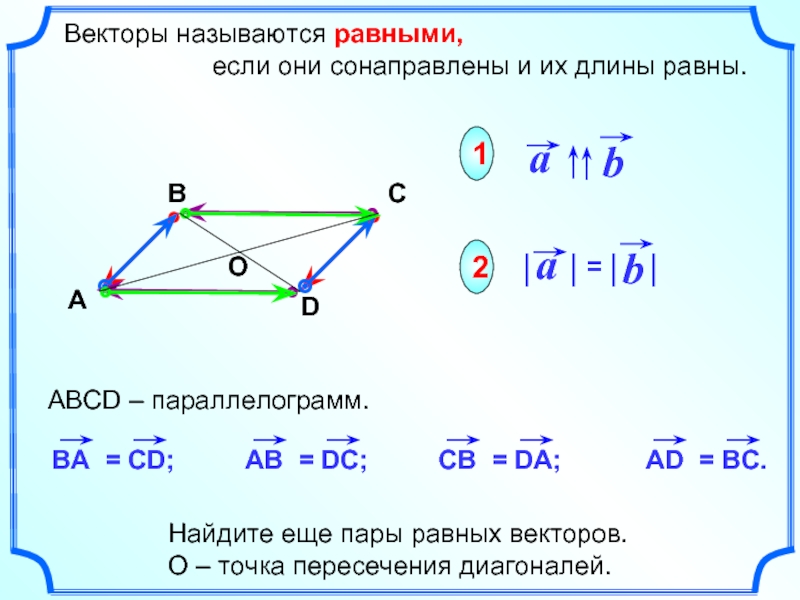
Слайд 10 Векторы называются равными,
1
2
Найдите еще пары равных векторов.
О – точка пересечения диагоналей.
Слайд 13
С
А
В
D
4
3
4
3
1,5
4
5
5
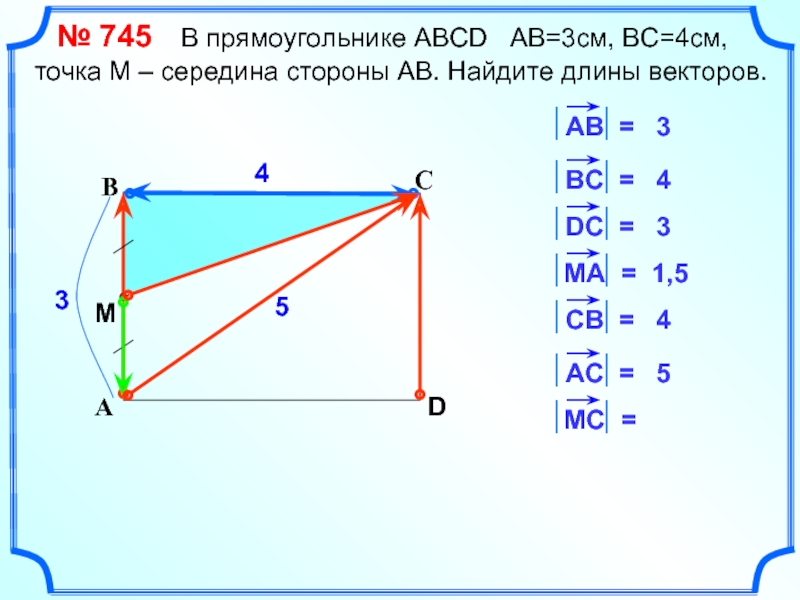
M
№ 745 В прямоугольнике АВСD АВ=3см, ВС=4см,
Слайд 14
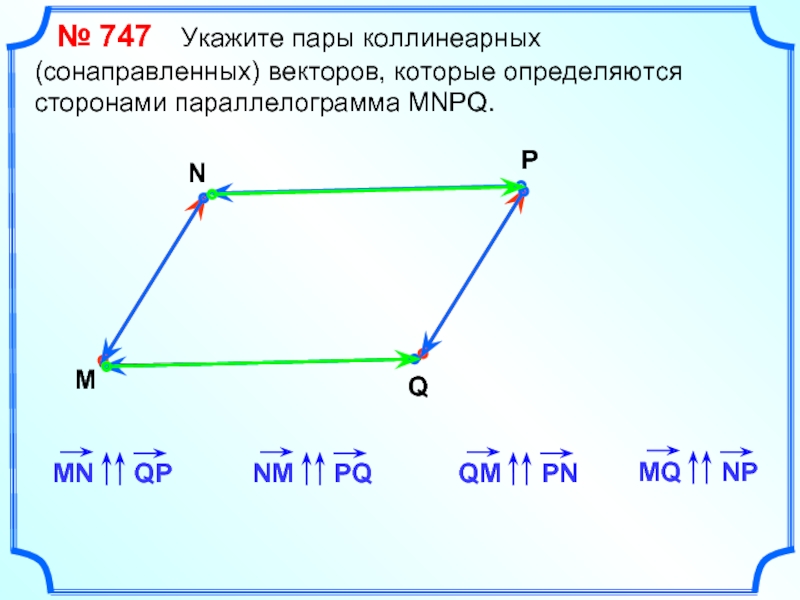
№ 747 Укажите пары коллинеарных
(сонаправленных) векторов, которые
M
N
P
Q
Слайд 15
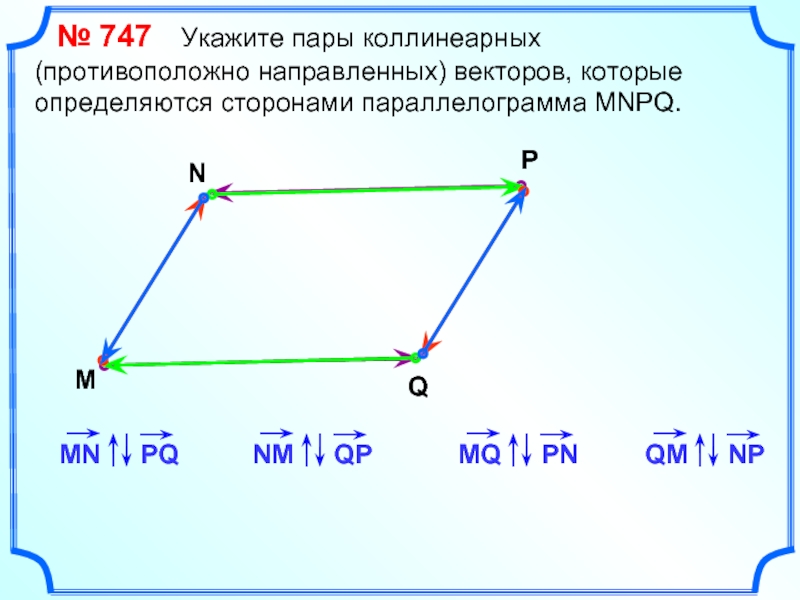
№ 747 Укажите пары коллинеарных
(противоположно направленных) векторов,
M
N
P
Q
Слайд 16
№ 747 Укажите пары коллинеарных
(сонаправленных) векторов, которые
А
В
С
D
Сонаправленные
векторы
Противоположно направленные
векторы
Слайд 17
№ 747 Укажите пары коллинеарных
векторов, которые определяются
F
G
H
Коллинеарных векторов нет
Слайд 18
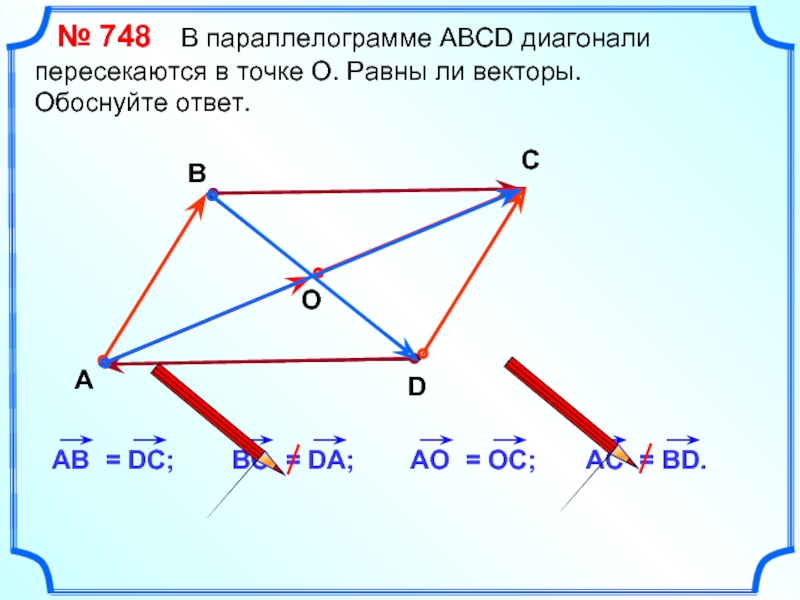
№ 748 В параллелограмме АВСD диагонали пересекаются в
Обоснуйте ответ.
А
В
С
D
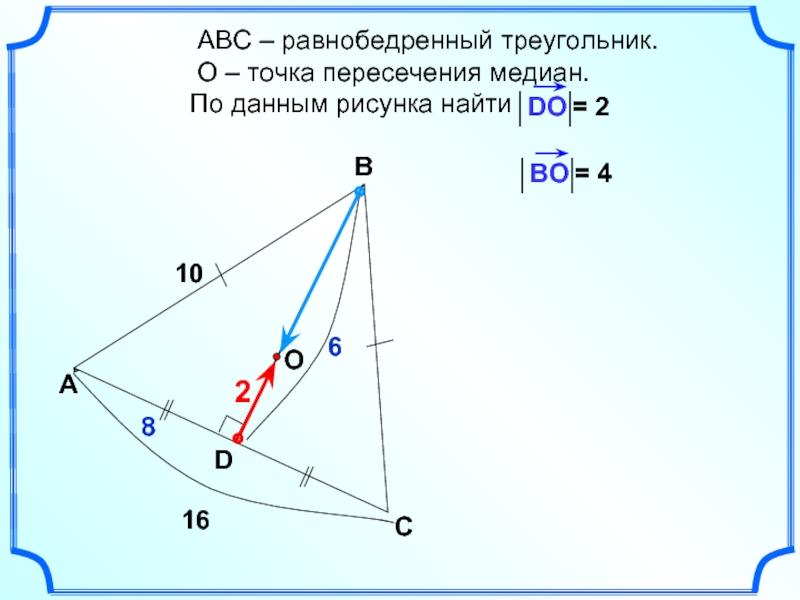
Слайд 21 АВС – равнобедренный треугольник.
О – точка пересечения
По данным рисунка найти
А
В
С
10
= 2
8
2
= 4
Слайд 23
№ 749 Точки S и Т являются серединами
Равны ли векторы.
M
N
L
K
S
T
Слайд 24
б) сонаправленные векторы;
в) противоположные векторы;
г) равные векторы;
д) векторы, имеющие равные длины.
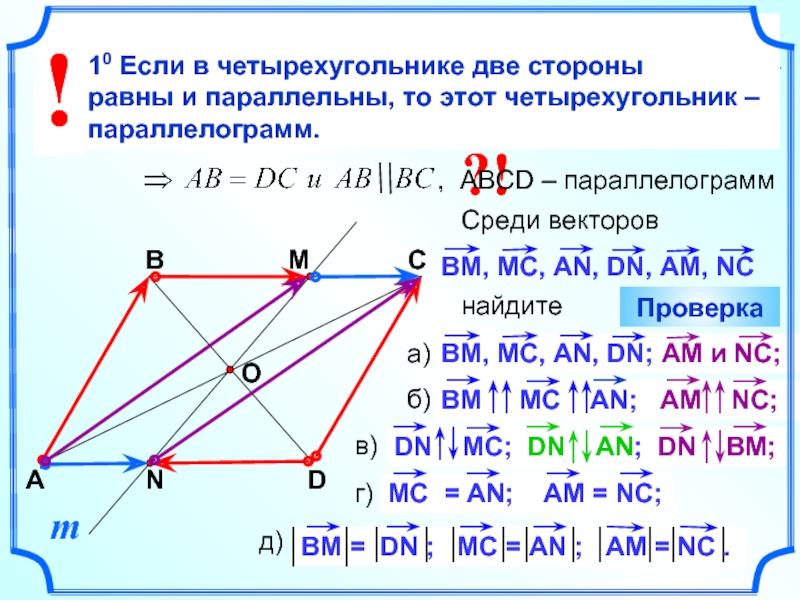
В четырехугольнике АВСD , О – точка пересечения диагоналей. Прямая проходит через точку О и пересекает стороны ВС и АD в точках М и N соответственно.
А
В
С
D
m
?!
Среди векторов
найдите
, АВСD – параллелограмм
Проверка