процессов
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численные методы решения нелинейных уравнений и систем нелинейных уравнений презентация
Содержание
- 1. Численные методы решения нелинейных уравнений и систем нелинейных уравнений
- 2. ЭТАПЫ ПРИБЛИЖЕННОГО ПОИСКА КОРНЕЙ НЕЛИНЕЙНОГО УРАВНЕНИЯ отделение
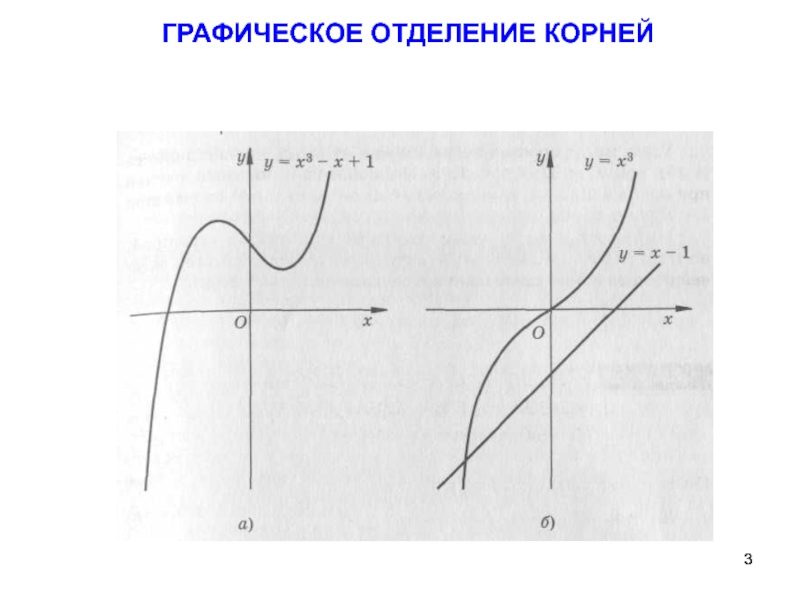
- 3. ГРАФИЧЕСКОЕ ОТДЕЛЕНИЕ КОРНЕЙ
- 4. ШАГОВОСТЬ И ПОРЯДОК СКОРОСТИ СХОДИМОСТИ Скорость
- 5. МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ Пусть действительный корень х0
- 6. МЕТОД ПРОСТОЙ ИТЕРАЦИИ НАХОЖДЕНИЯ КОРНЕЙ НЕЛИНЕЙНЫХ
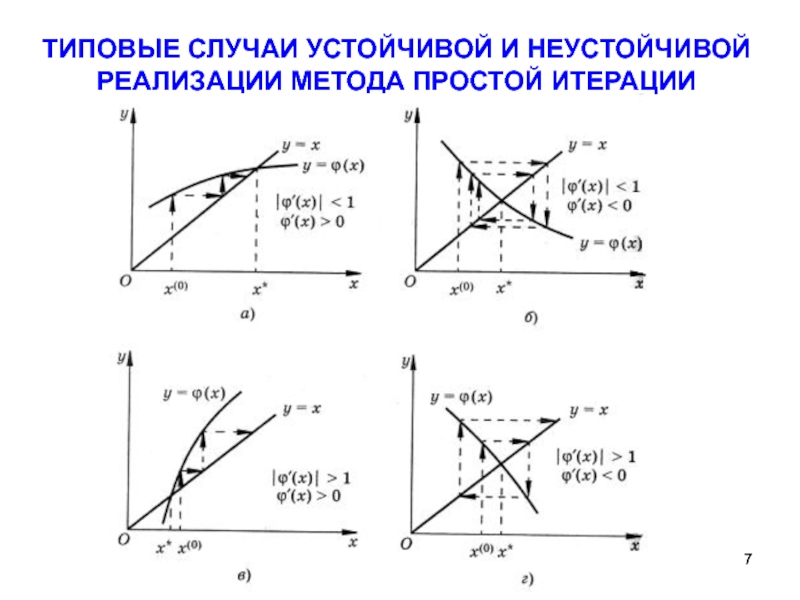
- 7. ТИПОВЫЕ СЛУЧАИ УСТОЙЧИВОЙ И НЕУСТОЙЧИВОЙ РЕАЛИЗАЦИИ МЕТОДА ПРОСТОЙ ИТЕРАЦИИ
- 8. КЛАССИЧЕСКИЙ ПРИМЕР ВЫЧИСЛЕНИЯ КВАДРАТНОГО КОРНЯ
- 9. МЕТОД НЬЮТОНА приближенное значение
- 10. Преимущества: квадратичная сходимость, возможность обобщения
- 11. МОДИФИЦИРОВАННЫЙ МЕТОД НЬЮТОНА Модифицированный метод –
- 12. МЕТОД СЕКУЩИХ (МЕТОД ХОРД) Идея: замена
- 13. МЕТОД ПРОСТОЙ ИТЕРАЦИИ НАХОЖДЕНИЯ КОРНЕЙ СИСТЕМ НЕЛИНЕЙНЫХ
- 14. МЕТОД ПРОСТОЙ ИТЕРАЦИИ НАХОЖДЕНИЯ КОРНЕЙ СИСТЕМ НЕЛИНЕЙНЫХ
- 15. СХОДИМОСТЬ МЕТОДА ПРОСТОЙ ИТЕРАЦИИ РЕШЕНИЯ НЕЛИНЕЙНОГО
- 16. МЕТОД ИТЕРАЦИЙ ЗЕЙДЕЛЯ МЕТОД НЬЮТОНА Приближенное значение корня Условие сходимости
- 17. МОДИФИЦИРОВАННЫЙ МЕТОД НЬЮТОНА Модифицированный метод –
- 18. Метод 2 – Метод простой итерации
ЭТАПЫ ПРИБЛИЖЕННОГО ПОИСКА КОРНЕЙ НЕЛИНЕЙНОГО УРАВНЕНИЯ отделение корня уточнение корня Отделение корня - это определение промежутка, содержащего один и только один корень уравнения. Одна из точек этого промежутка принимается
Слайд 1ЧИСЛЕННЫЕ МЕТОДЫ
решения нелинейных уравнений и систем нелинейных уравнений
Математическое моделирование систем и
Слайд 2ЭТАПЫ ПРИБЛИЖЕННОГО ПОИСКА КОРНЕЙ НЕЛИНЕЙНОГО УРАВНЕНИЯ
отделение корня
уточнение корня
Отделение корня -
это определение промежутка, содержащего один и только один корень уравнения.
Одна из точек этого промежутка принимается за начальное приближение корня.
Одна из точек этого промежутка принимается за начальное приближение корня.
Слайд 4ШАГОВОСТЬ И ПОРЯДОК СКОРОСТИ СХОДИМОСТИ
Скорость сходимости процесса
Метод является n-шаговым, если
для построения итерационной последовательности нужно вычислить функцию в n точках.
Шаговость процесса
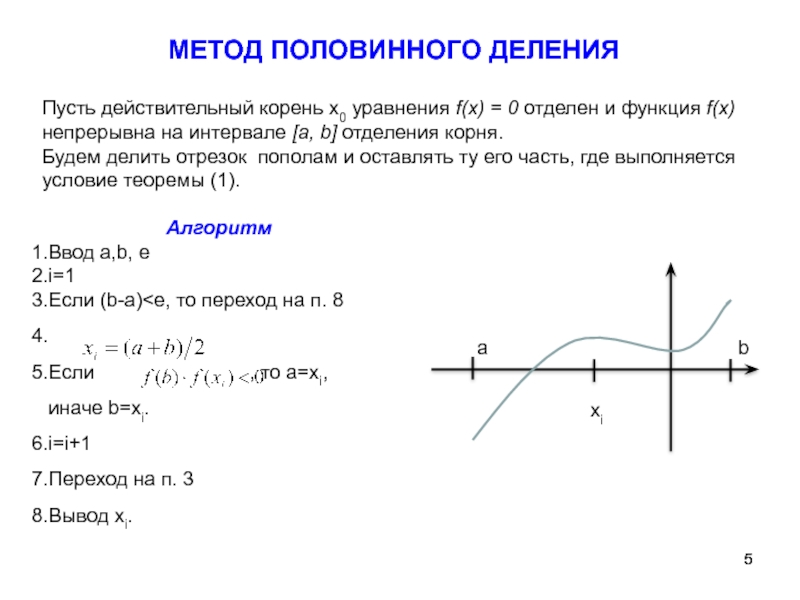
Слайд 5МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ
Пусть действительный корень х0 уравнения f(x) = 0 отделен
и функция f(x) непрерывна на интервале [a, b] отделения корня.
Будем делить отрезок пополам и оставлять ту его часть, где выполняется условие теоремы (1).
Будем делить отрезок пополам и оставлять ту его часть, где выполняется условие теоремы (1).
Алгоритм a b xi
Ввод а,b, e
i=1
Если (b-a)
Если , то a=xi,
иначе b=xi.
i=i+1
Переход на п. 3
Вывод xi.
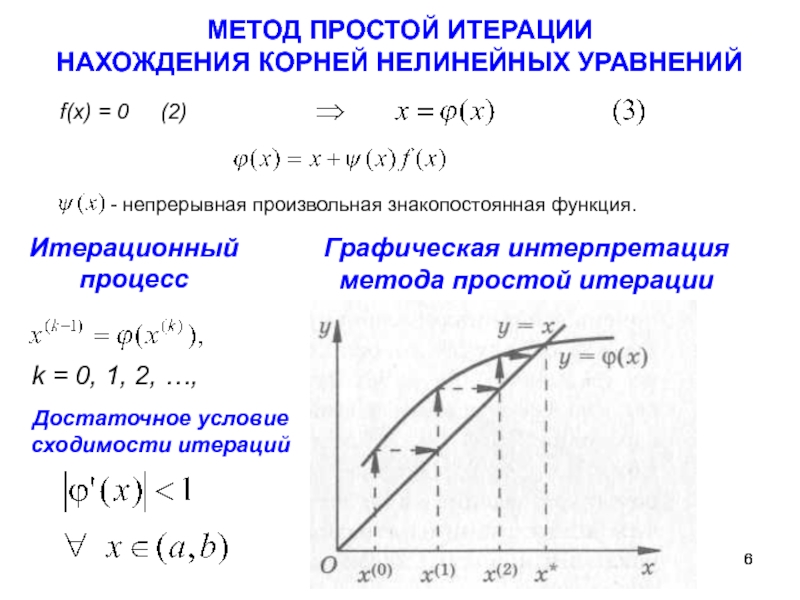
Слайд 6МЕТОД ПРОСТОЙ ИТЕРАЦИИ
НАХОЖДЕНИЯ КОРНЕЙ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
f(x) = 0
(2)
- непрерывная произвольная знакопостоянная функция.
Итерационный
процесс
k = 0, 1, 2, …,
Графическая интерпретация
метода простой итерации
Достаточное условие сходимости итераций
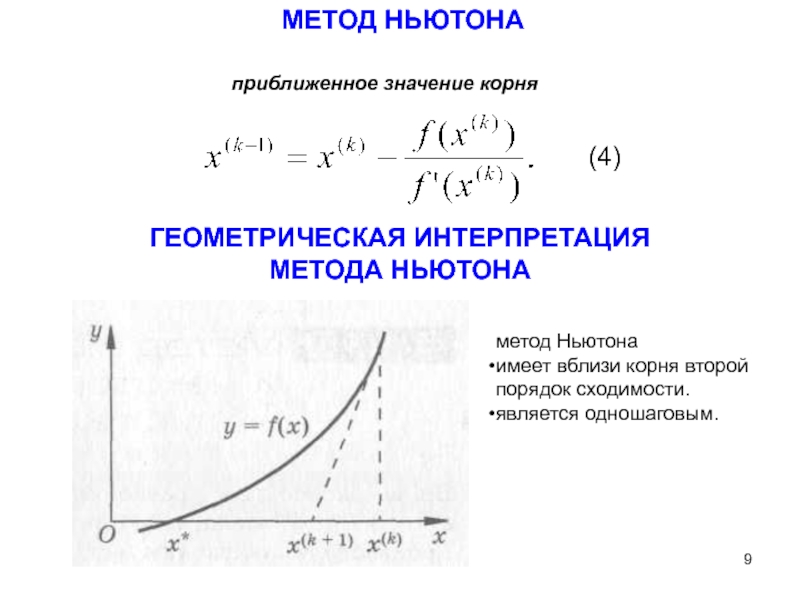
Слайд 9МЕТОД НЬЮТОНА
приближенное значение корня
(4)
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ МЕТОДА НЬЮТОНА
метод Ньютона
имеет вблизи корня второй
порядок сходимости.
является одношаговым.
является одношаговым.
Слайд 10Преимущества:
квадратичная сходимость,
возможность обобщения на случай систем уравнений,
метод является
одношаговым.
ПРЕИМУЩЕСТВА И НЕДОСТАТКИ
МЕТОДА НЬЮТОНА
Недостатки:
Расходится в тех областях,
где
2) если функция f(x) задана таблично,
то вычисление затруднено
Пути устранения:
Метод секущих
Модифицированный метод Ньютона
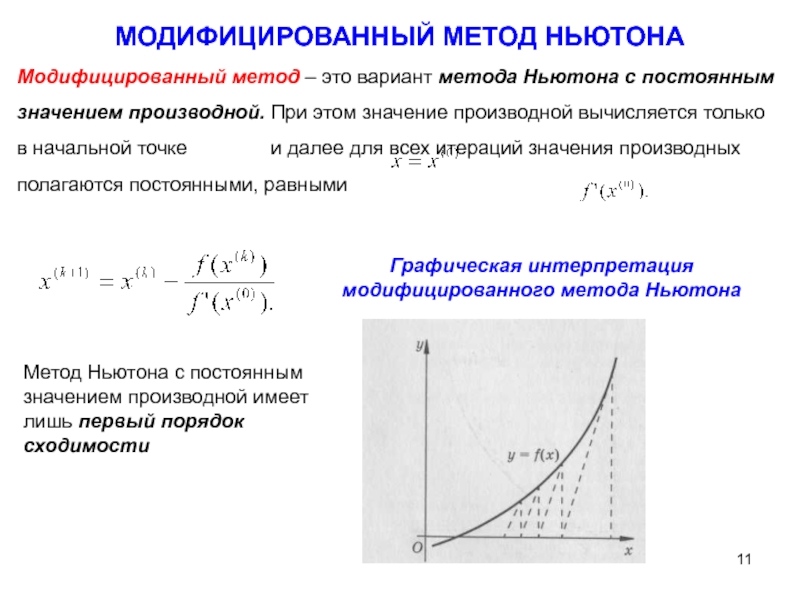
Слайд 11МОДИФИЦИРОВАННЫЙ МЕТОД НЬЮТОНА
Модифицированный метод – это вариант метода Ньютона с
постоянным значением производной. При этом значение производной вычисляется только в начальной точке и далее для всех итераций значения производных полагаются постоянными, равными
Графическая интерпретация модифицированного метода Ньютона
Метод Ньютона с постоянным значением производной имеет лишь первый порядок сходимости
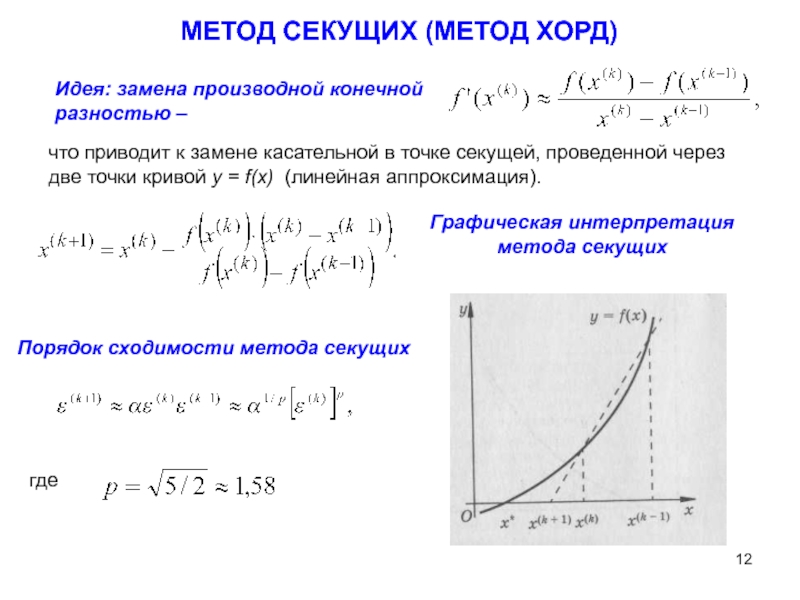
Слайд 12МЕТОД СЕКУЩИХ (МЕТОД ХОРД)
Идея: замена производной конечной разностью –
что
приводит к замене касательной в точке секущей, проведенной через две точки кривой y = f(x) (линейная аппроксимация).
Графическая интерпретация
метода секущих
Порядок сходимости метода секущих
где
Слайд 13МЕТОД ПРОСТОЙ ИТЕРАЦИИ НАХОЖДЕНИЯ КОРНЕЙ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
f(x) = 0
(1)
- вектор-столбец неизвестных,
- вектор-столбец функций
или
(3)
Слайд 14МЕТОД ПРОСТОЙ ИТЕРАЦИИ НАХОЖДЕНИЯ КОРНЕЙ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Итерационный процесс
Начальное приближение для
корня
Формула расчета значения на (k+1) итерации
или
Вектор погрешности испытывает линейное преобразование,
(метод имеет первый порядок сходимости)
Слайд 15СХОДИМОСТЬ МЕТОДА ПРОСТОЙ ИТЕРАЦИИ
РЕШЕНИЯ НЕЛИНЕЙНОГО УРАВНЕНИЯ
Достаточное условие сходимости итераций
МАТРИЦА ЯКОБИ
ФУНКЦИЙ
Система принимает вид:
Слайд 17МОДИФИЦИРОВАННЫЙ МЕТОД НЬЮТОНА
Модифицированный метод – это вариант метода Ньютона с
постоянным значением производной.
Метод Ньютона с постоянным значением производной имеет первый порядок сходимости:
