- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Булеві функції презентация
Содержание
- 1. Булеві функції
- 2. 4.7. Мінімізація булевих функцій метод карт Карно
- 3. Задача мінімізації складається з пошуку найпростішої, згідно
- 4. Множина S, що складається з імплікант функції
- 5. Простою імплікантою функції f називається така кон'юнкція-імпліканта,
- 6. Диз'юнктивним ядром булевої функції f називається така
- 7. Для знаходження множини простих імплікант функції, що
- 8. Приклад. Нехай є функція f, що задана
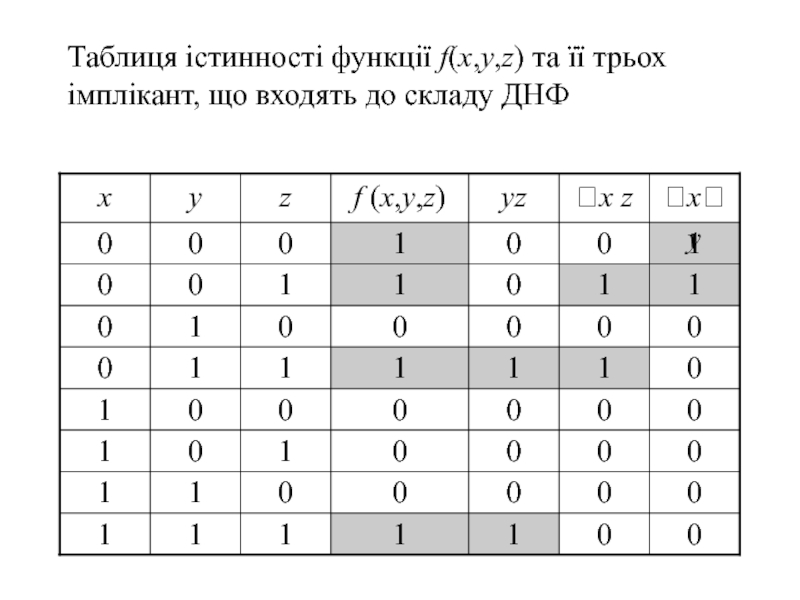
- 9. Таблиця істинності функції f(x,у,z) та її трьох імплікант, що входять до складу ДНФ
- 10. Для аналізу різних зображень булевої функції через
- 11. Мінімізація булевих функцій методом карт Карно
- 12. Структура карти Карно для двох змінних
- 13. До конституент одиниці, що відповідають будь-яким двом
- 14. Приклад. Побудувати карту Карно для функції
- 15. Правило склеювання кліток і запису МДНФ
- 16. 5. Кожна група кліток, що одержана після
- 17. Приклад. Побудувати карту Карно для
- 18. Приклад. Знайти МДНФ для
- 19. МДНФ: f(x, у, z, t) =
- 20. Мінімізація булевих функцій методом діаграм Вейча
- 21. МКНФ: f(x, у, z, t) =
- 22. Мінімізація частково визначених функцій Якщо для розв'язку
- 23. МДНФ: f(x, у, z, t) =
- 24. МДНФ: f(x, у, z, t) =
- 25. Характеристика методів Карно та Вейча Методи не
- 26. Мінімізація булевих функцій методом Нельсона
- 27. Розв'язок. f(x, у, z) = (х
- 28. Характеристика методу Нельсона Метод є формальним, але
- 29. Мінімізація булевих функцій методом Квайна
- 30. 4. Скласти імплікантну таблицю і знайти
- 31. Розв'язок. Виконаємо всі можливі операції диз'юнктивного склеювання
- 32. Імплікантна таблиця функції f(x, у, z)
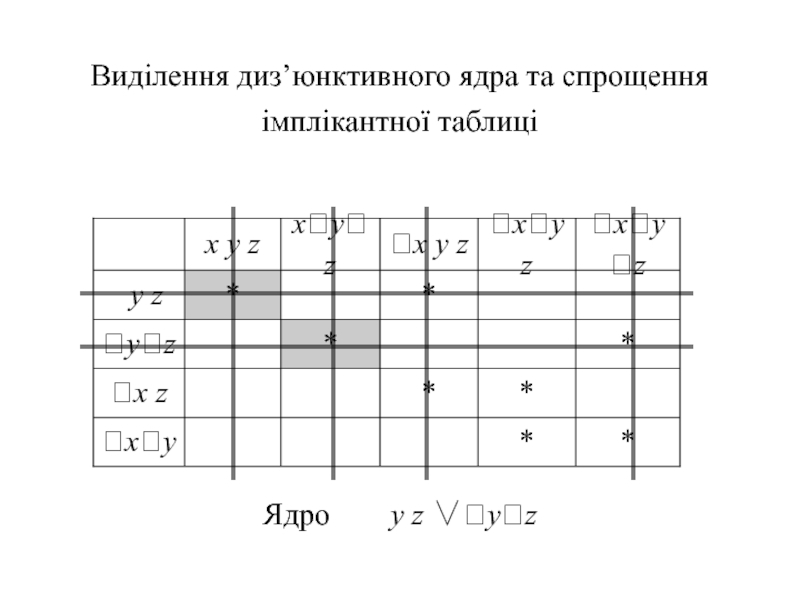
- 33. Виділення диз’юнктивного ядра та спрощення імплікантної таблиці Ядро у z ∨yz
- 34. За спрощеною імплікантною таблицею знаходимо тупикові ДНФ
- 35. Характеристика методу Квайна Метод є формальним, але
- 36. Мінімізація булевих функцій методом Мак-Класкі
- 37. Конституенти одиниці записуються у вигляді двійкового
- 38. Виконання операцій склеювання здійснюється покроково. На
- 39. 1. Згрупувати двійкові коди імплікант з
- 40. Розв'язок. Запишемо конституенти одиниці даної функції у
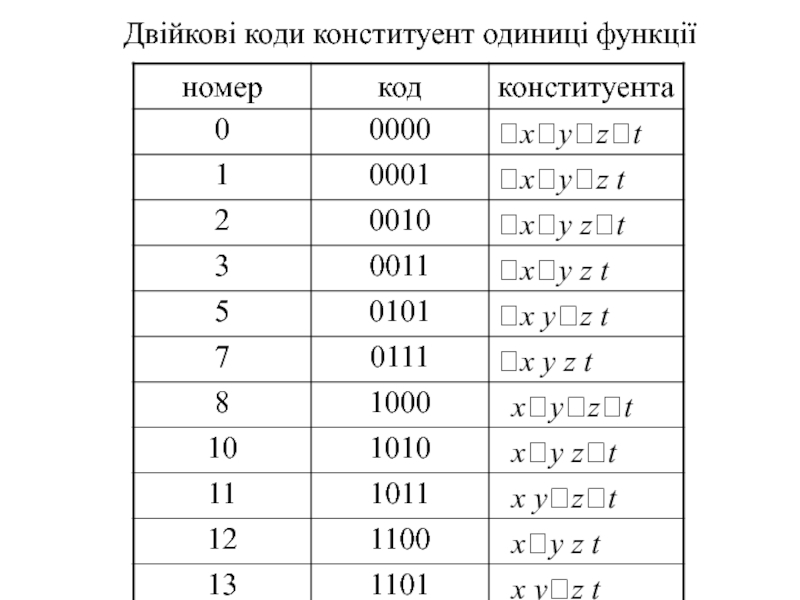
- 41. Двійкові коди конституент одиниці функції
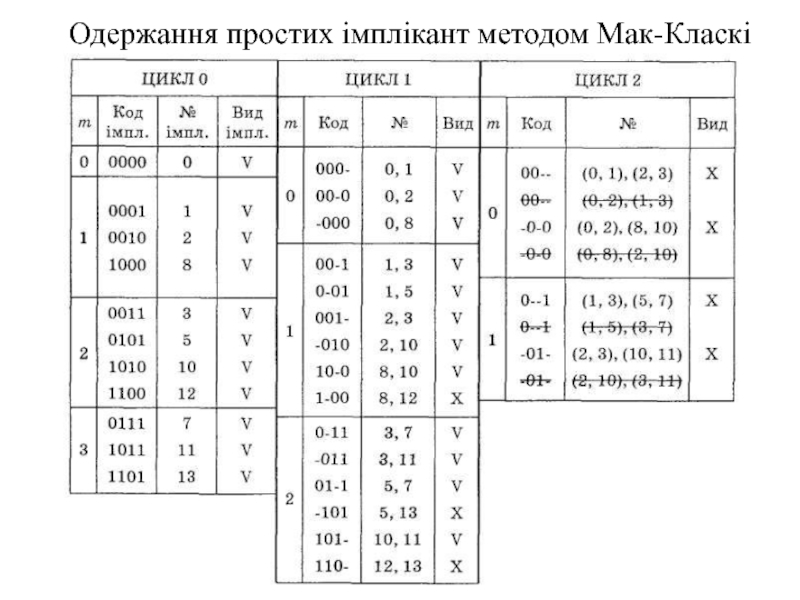
- 42. Одержання простих імплікант методом Мак-Класкі
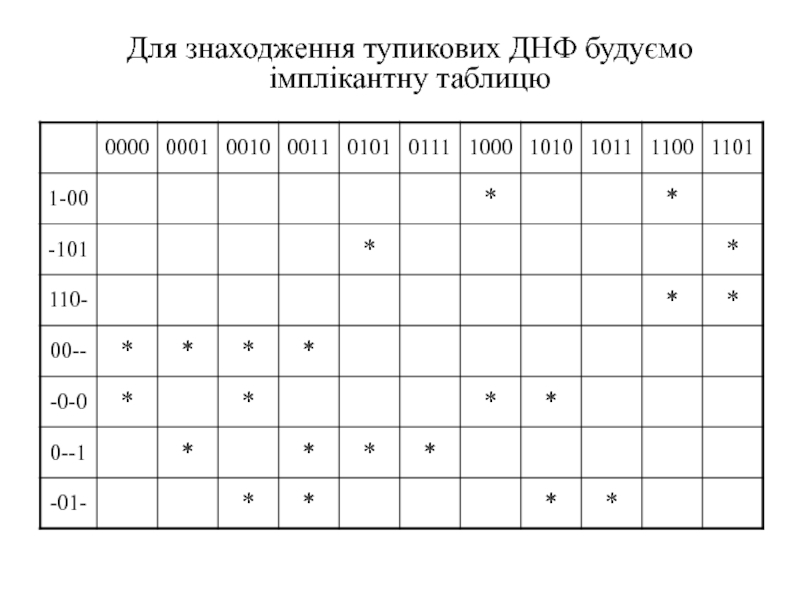
- 43. Для знаходження тупикових ДНФ будуємо імплікантну таблицю
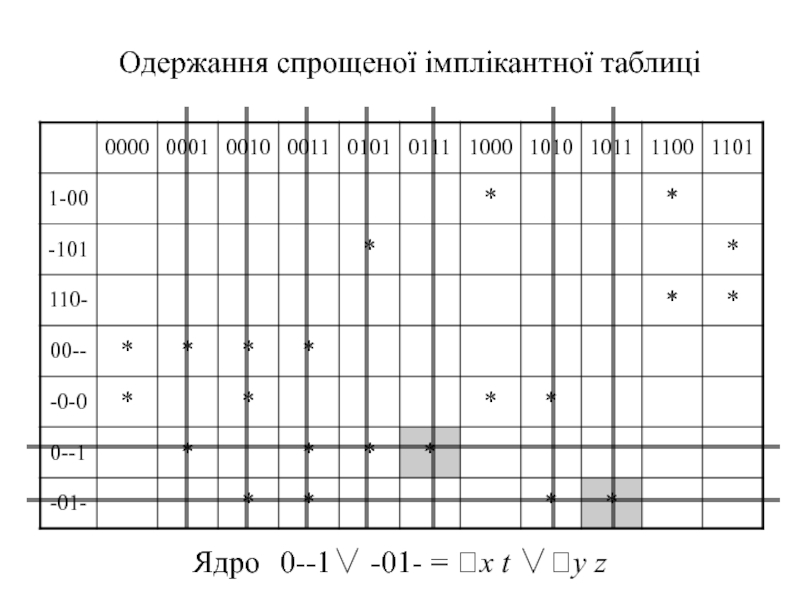
- 44. Одержання спрощеної імплікантної таблиці Ядро 0--1∨ -01- = x t ∨y z
- 45. Cпрощена імплікантна таблиця Метод Петрика для
- 46. Характеристика методу Мак-Класкі Метод є формальним, не
- 47. Мінімізація булевих функцій методом Блейка —
- 48. Розв'язок. Узагальнене склеювання: xyz ∨ xz =
- 49. Характеристика методу Блейка — Порецького
- 50. 4.8. Алгебра Жегалкіна структура алгебри Жегалкіна тотожності
- 51. Алгебра (В, ∧, ⊕, 0, 1), що
- 52. Тотожності алгебри Жегалкіна Властивості кон'юнкції: 1)
- 53. Зображення заперечення: х = х ⊕
- 54. Поліном Жегалкіна Поліномом Жегалкіна називається скінченна сума
- 55. Побудова поліному Жегалкіна аналітичним способом
- 56. Розв'язок. Спочатку запишемо ДДНФ даних функцій, потім
- 57. Розв'язок. Проаналізуємо структуру формул, що виведені у
- 58. Розв'язок. Побудуємо поліном Жегалкіна функції f(х, у,
- 59. Побудова поліному Жегалкіна методом невизначених коефіцієнтів
- 60. Розв'язок. Запишемо поліном для даної функції у
- 61. f13(0, 1) = 0 → 1 =
- 62. Функції, що зберігають нуль та одиницю
- 63. Приклад. Визначте, чи зберігає 0 та 1
- 64. Розглянемо важливий клас булевих функцій — монотонні
- 65. Приклад. Дослідити на монотонність функцію f(x,
- 66. Приклад. Дослідити на монотонність функцію g(x,
- 67. Теорема. Булева функція, відмінна від констант 0
Слайд 24.7. Мінімізація булевих функцій
метод карт Карно
метод діаграм Вейча (мінімізація на множині
мінімізація частково визначених функцій
метод Нельсона
метод Квайна
метод Мак-Класкі
метод Порецького — Блейка
Слайд 3 Задача мінімізації складається з пошуку найпростішої, згідно з обраним критерієм, формули.
Канонічною задачею мінімізації називається задача мінімізації на множині ДНФ і КНФ кількості символів змінних та операцій, що містяться у формулі. Мінімальні форми, що одержані в результаті її розв'язку, називаються мінімальними ДНФ і КНФ.
Імплікантою деякої функції f називається функція g, така, що на всіх інтерпретаціях, на яких g дорівнює одиниці, f теж дорівнює одиниці.
Конституенти одиниці функції є її імплікантами; елементарні кон'юнкції, що входять до складу ДНФ функції, також є її імплікантами.
Слайд 4Множина S, що складається з імплікант функції f, називається покриттям (або
Набір імплікант, складових ДНФ функції, є її покриттям. Набір всіх конституент одиниці функції, що входять до її ДДНФ, є покриттям даної функції.
Будь-яку елементарну кон'юнкцію А, що входить до складу елементарної кон'юнкції В і містить менше змінних, ніж кон'юнкція В, називають власною частиною кон'юнкції В, і вважають, що кон'юнкція А покриває кон'юнкцію В.
Слайд 5Простою імплікантою функції f називається така кон'юнкція-імпліканта, що ніяка її власна
Мінтерми функції є її імплікантами, елементарні кон'юнкції, що входять до складу ДНФ функції, також є її імплікантами.
Множина всіх простих імплікант функції становить покриття даної функції.
Диз'юнкція всіх простих імплікант функції називається її скороченою ДНФ.
Слайд 6Диз'юнктивним ядром булевої функції f називається така множина її простих імплікант,
Тупиковою ДНФ називається ДНФ даної булевої функції, що складається тільки з простих імплікант.
Кожна булева функція має єдину скорочену ДНФ і може мати декілька тупикових ДНФ. У кожну з тупикових ДНФ входять всі імпліканти диз'юнктивного ядра даної функції.
Мінімальною ДНФ (МДНФ) даної булевої функції називається одна з її тупикових ДНФ, якій відповідає найменше значення критерію мінімізації ДНФ.
Слайд 7 Для знаходження множини простих імплікант функції, що задана СДНФ, використовуються такі
операція неповного диз'юнктивного склеювання:
А х ∨ Ах = A ∨ A x ∨ Ах.
операція диз'юнктивного поглинання:
A ∨ А х = А.
Виконання обох операцій послідовно - це
операція повного диз'юнктивного склеювання:
А х ∨ Ах = А.
Тут А — деяка елементарна кон'юнкція змінних,
х — булева змінна.
Слайд 8Приклад. Нехай є функція f, що задана ДДНФ:
f(x, у, z) =
Виконаємо операції повного склеювання :
f(x, у, z) = х у z ∨x y z ∨xy z ∨xyz =
= (х у z ∨x y z)∨(x y z ∨xy z )∨(xy z ∨xyz) =
= у z ∨x z ∨xy.
Виконаємо операції склеювання іншим способом:
f(x, у, z) = (х у z ∨x y z)∨(xy z ∨xyz) = у z ∨xy.
В обох випадках одержані тупикові ДНФ функції f(x,у,z). Друга тупикова ДНФ простіша за першу, оскільки містить меншу кількість символів змінних і знаків операцій.
Слайд 10Для аналізу різних зображень булевої функції через КНФ і одержання мінімальних
Використовувані для мінімізації КНФ операції склеювання мають такий вигляд:
Операція неповного кон'юнктивного склеювання:
(A ∨ x)(A ∨х) = А(А ∨ x)(A ∨x).
Операція кон'юнктивного поглинання:
А(А ∨ х) = А.
Операція повного кон'юнктивного склеювання:
(A ∨ x)(A ∨x)=A.
Слайд 11Мінімізація булевих функцій
методом карт Карно
Ціллю мінімізації є знаходження мінімальної з
Для цього необхідно побудувати всі можливі тупикові ДНФ (КНФ), використовуючи операції склеювання та поглинання для даної функції. Методика Карно і Вейча дозволяє виконати ці операції графічно.
Слайд 12Структура карти Карно для двох змінних
Структура карти Карно для трьох
Карта Карно для ДНФ (діаграма Вейча — для КНФ) є аналогом таблиці істинності, зображеній у спеціальній формі.
Слайд 13 До конституент одиниці, що відповідають будь-яким двом сусіднім кліткам, можна застосувати
Слайд 15Правило склеювання кліток і запису МДНФ
1. Побудувати карту Карно, що відповідає
2. Клітки об'єднуються у групи, що позначають операції склеювання. В об'єднанні беруть участь тільки сусідні клітки, в яких знаходяться одиниці.
3. В групу можні об'єднати кількість кліток, що дорівнює 2n, n = 1, 2, 3, .... При цьому група може мати тільки прямокутну або квадратну форму.
4. Задача склеювання полягає у знаходженні набору максимальних груп кліток. Кількість груп у наборі повинна бути мінімальною, оскільки така група відповідає мінімальній тупиковій ДНФ. Кожна одиниця карти Карно повинна входити хоча б до однієї групи, що забезпечує покриття функції одержаним набором імплікант.
Слайд 165. Кожна група кліток, що одержана після склеювання, відповідає тій імпліканті
6. Диз'юнкція всіх одержаних простих імплікант є мінімальною ДНФ.
Слайд 17
Приклад. Побудувати карту Карно для функції
f(x, у, z) = х
А В
Імпліканта А = xy z ∨xyz = xy (z ∨z )= xy.
Імпліканта B = х у z ∨x y z = (x ∨x) у z = у z.
МДНФ: f(x, у, z) = A ∨ В = xy ∨ у z.
Слайд 18
Приклад. Знайти МДНФ для функції
f(x, у, z) =х уz ∨
А В С
МДНФ f(x, у, z) = A ∨ B ∨ C =xy z ∨ yz ∨ x y.
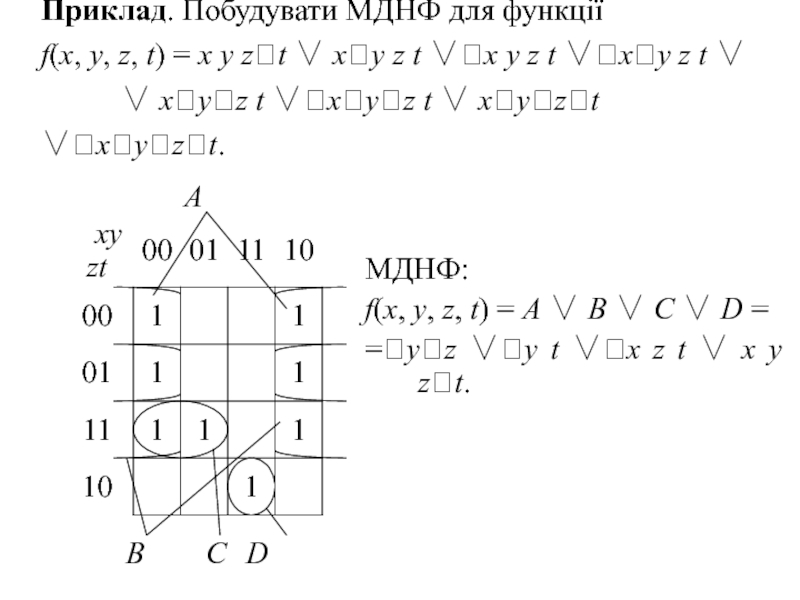
Слайд 19МДНФ:
f(x, у, z, t) = A ∨ В ∨ C
=уz ∨у t ∨x z t ∨ x у zt.
A
В C D
Приклад. Побудувати МДНФ для функції
f(x, у, z, t) = x у zt ∨ xу z t ∨x у z t ∨xу z t ∨
∨ xуz t ∨xуz t ∨ xуzt ∨xуzt.
Слайд 20Мінімізація булевих функцій
методом діаграм Вейча
Для мінімізації булевої функції на множині
Слайд 21МКНФ:
f(x, у, z, t) = A ∧ В ∧ C
= (у ∨ z) ∧ (у ∨z ∨ t) ∧
∧(x ∨z ∨ t) ∧ (x ∨у ∨t).
A
В C D
Приклад. Побудувати МКНФ для функції
f(x, у, z, t) = x у zt ∨ xу z t ∨x у z t ∨xу z t ∨
∨ xуz t ∨xуz t ∨ xуzt ∨xуzt.
Слайд 22Мінімізація частково визначених функцій
Якщо для розв'язку задачі використовуються не всі набори
Слайд 23МДНФ:
f(x, у, z, t) = A ∨ В = zt
А В
Приклад. Функція f(x, у, z, t) дорівнює одиниці на наборах (0,0,1,0), (0,1,1,0), (1,0,1,0), (1,0,0,0) і не визначена, якщо ху = 1. Необхідно побудувати МДНФ та МКНФ.
Слайд 24МДНФ:
f(x, у, z, t) = A ∨ В = zt
C D
МКНФ:
f(x, у, z, t) = C ∧ D =t ∧ (x ∨ z).
Приклад. Функція f(x, у, z, t) дорівнює одиниці на наборах (0,0,1,0), (0,1,1,0), (1,0,1,0), (1,0,0,0) і не визначена, якщо ху = 1. Необхідно побудувати МДНФ та МКНФ.
Слайд 25Характеристика методів Карно та Вейча
Методи не є формальними і складні для
Методи не зручні у застосуванні до функцій з кількістю змінних більше шести.
Перевагою методів є простота сприйняття та вивчення для людини.
Слайд 26Мінімізація булевих функцій
методом Нельсона
Метод мінімізації Нельсона реалізує перехід від КНФ
1. Записати КНФ заданої функції.
2. Розкрити дужки за дистрибутивним законом, спростити і звести подібні (закони ідемпотентності й протиріччя).
3. Виконати всі можливі операції диз'юнктивного поглинання. Результуюча формула є CДНФ функції.
Слайд 27Розв'язок.
f(x, у, z) = (х ∨y)(x ∨ z)(x ∨ y
= (хx ∨yx ∨ х z ∨y z )(x ∨ y ∨z) =
= хx x ∨yx x ∨ х z x ∨y z x ∨ хx y ∨yx y ∨
∨ х z y ∨y z y ∨ хxz ∨yxz ∨ х zz ∨y zz =
= х z ∨ xy z ∨ х y z ∨xyz
Приклад. Знайти методом Нельсона СДНФ функції
f(x, у, z) = (х ∨y)(x ∨ z)(x ∨ y ∨z).
Слайд 28Характеристика методу Нельсона
Метод є формальним, але складний для програмної реалізації.
Метод
Результатом є скорочена, а не мінімальна форма. Для отримання мінімальної форми треба скористатися ще якимось методом.
Слайд 29Мінімізація булевих функцій
методом Квайна
Метод мінімізації Квайна також реалізує перехід від
1. Записати ДДНФ заданої функції.
2. Виконати всі можливі операції неповного диз'юнктивного склеювання. Результуюча формула є диз'юнкцією всіх можливих імплікант даної функції.
3. Виконати всі можливі операції диз'юнктивного поглинання. Результуюча формула є CДНФ функції.
Слайд 304. Скласти імплікантну таблицю і знайти диз'юнктивне ядро.
5. Спростити
6. Знайти всі тупикові ДНФ даної функції.
7. Знайти мінімальну ДНФ.
Слайд 31Розв'язок. Виконаємо всі можливі операції диз'юнктивного склеювання і поглинання:
f(x, у,
∨ y z
= у z ∨yz ∨x z ∨xy
∨yz
∨x z
∨xy =
Приклад. Знайти методом Квайна МДНФ функції
f(x, у, z) = х у z ∨ xyz ∨x y z ∨xy z ∨xyz.
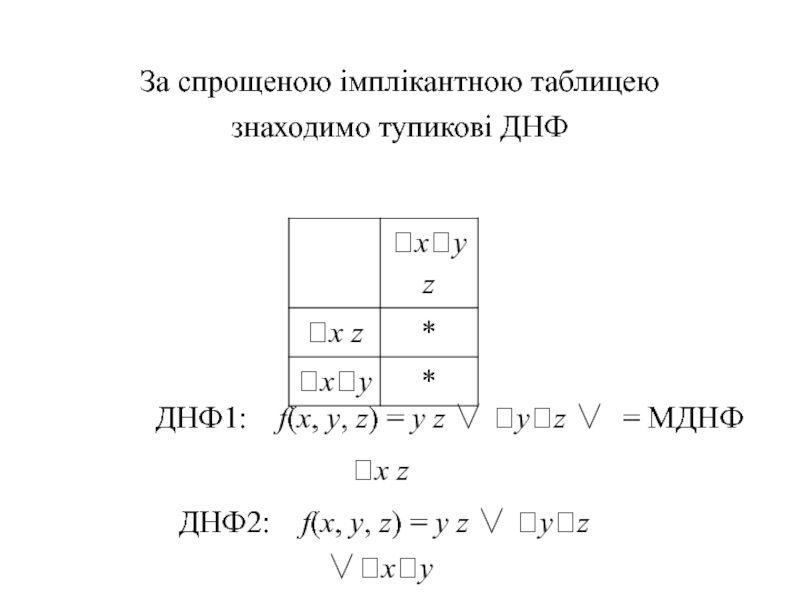
Слайд 34За спрощеною імплікантною таблицею знаходимо тупикові ДНФ
ДНФ1: f(x, у,
ДНФ2: f(x, у, z) = у z ∨ yz ∨xy
= МДНФ
Слайд 35Характеристика методу Квайна
Метод є формальним, але складний для програмної реалізації.
Вихідними
Для функції великого числа змінних перелічення варіантів склеювання і множини тупикових ДНФ є значною складністю.
Слайд 36Мінімізація булевих функцій
методом Мак-Класкі
Метод мінімізації Мак-Класкі є переробкою методу Квайна.
Слайд 37
Конституенти одиниці записуються у вигляді двійкового коду — номеру конституенти. Імпліканти,
Множина кодів імплікант ділиться на групи за кількістю одиниць, що в них утримуються. Оскільки операції неповного склеювання застосовні до імплікант, коди яких відрізняються значенням тільки в одній позиції, в склеюванні можуть брати участь тільки імпліканти, що належать до сусідніх груп, номери яких відрізняються на одиницю.
Слайд 38
Виконання операцій склеювання здійснюється покроково. На першому кроці здійснюються всі можливі
При виконанні операцій поглинання з формули видаляються всі імпліканти, що не є простими, тобто брали участь хоча б в одному склеюванні. Результуюча формула зображує диз'юнкцію простих імплікант функції — її скорочену ДНФ.
Слайд 391. Згрупувати двійкові коди імплікант з однаковою кількістю одиниць. Число
2. Починаючи з m = 0, порівнянти кожний двійковий код в групі з індексом m з кожним кодом з групи з індексом m + 1. Якщо вони різні тільки в одному розряді, то у наступний стовпчик таблиці записати відповідний їм двійковий код з порожньою позначкою «-» на місці зазначеного розряду. Імпліканти, що брали участь у заміні, не є простими, позначити їх знаком «V». Решту кодів позначити «Х» (це прості імпліканти).
3. Якщо серед знов одержаних імплікант є однакові, то з них для подальшого використання залишити тільки одну.
4. Повторювати кроки 1-3 доти, доки існує можливість одержувати нові коди імплікант.
Слайд 40Розв'язок. Запишемо конституенти одиниці даної функції у вигляді двійкових кодів
Приклад.
Слайд 45Cпрощена імплікантна таблиця
Метод Петрика
для знаходження тупикових ДНФ і вибору з
(D ∨ E)(A ∨ E)(A ∨ C)(B ∨ C) = DAB ∨ EAB ∨ DAC ∨ EC
Кожна кон'юнкція буквених позначень відповідає набору імплікант у деякій тупиковій ДНФ, до якої обов'язково входить також диз'юнктивне ядро.
МДНФ f(x, у, z, t) = уt ∨ x уz ∨x t ∨у z .
Слайд 46Характеристика методу Мак-Класкі
Метод є формальним, не складний для програмної реалізації.
Недолік
Слайд 47Мінімізація булевих функцій
методом Блейка — Порецького
Метод Блейка — Порецького
Операція узагальненого склеювання:
Ах ∨ Вх = Ах ∨ Вх ∨ AB.
Доведення:
Ах∨Вх = Ax(l∨В)∨Вх(1∨А) = Ах∨ABx∨Bx∨ABx =
= Ах ∨ Bx ∨ АВ(х ∨х) = Ах ∨ Bx ∨ AB.
Операція поглинання:
Ах ∨ А = А.
Слайд 48Розв'язок. Узагальнене склеювання:
xyz ∨ xz = xy ∨ xyz ∨ xz
xyz ∨xy= yz ∨ xyz ∨xy, A = yz, В = у;
xz ∨xy= yz ∨ xz ∨xy, A = z, В = у.
До одержаних імплікант може бути застосована операція повного диз'юнктивного склеювання:
yz ∨ yz = у, xy ∨xy = у.
Вихідна формула прийме такий вигляд:
f(x, у, z) = (xy ∨xy) ∨ xyz ∨ xz ∨ (yz ∨ yz) =
= у ∨ xyz ∨ xz ∨ у = y(xz ∨ 1) ∨ xz = y ∨ xz.
Отже, f = y ∨ xz є скорочена ДНФ.
Приклад. Знайти скорочену ДНФ за методом
Блейка — Порецького для функції
f(x, у, z) = xyz ∨ xz ∨xy.
Слайд 49Характеристика методу
Блейка — Порецького
Метод є формальним, але складний для
Метод дозволяє здійснювати диз'юнктивну мінімізацію, використовуючи як вихідну довільну ДНФ функції.
Результатом є скорочена, а не мінімальна форма. Для отримання мінімальної форми треба скористатися ще якимось методом.
Слайд 504.8. Алгебра Жегалкіна
структура алгебри Жегалкіна
тотожності алгебри Жегалкіна
поліномом Жегалкіна
лінійність булевих функцій
функції,
монотонні функції
Слайд 51Алгебра (В, ∧, ⊕, 0, 1), що утворена множиною В={0, 1}
В алгебрі Жегалкіна операція кон'юнкції повністю ідентична множенню, а операція XOR зображує додавання за модулем для скінченних множин.
Приклад. Формула (х⊕у⊕z)∧(х⊕z⊕1)⊕х∧у⊕1, де х, у, z — булеві змінні, є прикладом формули алгебри Жегалкіна, тому що вона містить операції кон'юнкції і XOR.
Будь-яка логічна функція може бути зображена формулою в алгебрі Жегалкіна.
Слайд 52Тотожності алгебри Жегалкіна
Властивості кон'юнкції:
1) х ∧ (у ∧ z) =
2) х ∧ у = у ∧х — комутативність
3) х ∧ х = х — ідемпотентність
4) х ∧ 0 = 0, х ∧ 1 = х — дії з константами
Властивості операції XOR (додавання за модулем 2):
5) х ⊕ (у ⊕ z) = (х ⊕ у) ⊕ z — асоціативність
6) х ⊕ у = у ⊕ х — комутативність операції XOR
7) х ⊕ х = 0 — закон зведення подібних доданків
8) х ⊕ 0 = х — операція з константою 0
9) х(у⊕z) = ху⊕xz — дистрибутивність ∧ відносно ⊕
Слайд 53Зображення заперечення:
х = х ⊕ 1
Зображення диз'юнкції:
x ∨
= (х ⊕ 1)(у ⊕ 1) ⊕ 1 = ху ⊕ у ⊕ х ⊕ 1 ⊕ 1 =
= ху ⊕ у ⊕ х.
Слайд 54Поліном Жегалкіна
Поліномом Жегалкіна називається скінченна сума за модулем 2 попарно різних
Кількість змінних, що входять до елементарної кон'юнкції, називається рангом елементарної кон'юнкції.
Кількість попарно різних елементарних кон'юнкцій у поліномі називається довжиною полінома.
Зображення у вигляді поліному існує та єдине для кожної булевої функції.
Булева функція називається лінійною, якщо її поліном Жегалкіна не містить кон'юнкцій змінних.
Слайд 55Побудова поліному Жегалкіна
аналітичним способом
Для побудови поліному Жегалкіна функції, що
Слайд 56Розв'язок. Спочатку запишемо ДДНФ даних функцій, потім виразимо операції диз'юнкції та
x → y =x ∨ y = (x ⊕ 1) ∨ y = (x ⊕ l) y ⊕ (x ⊕ l) ⊕ y =
= ху ⊕ у ⊕ х ⊕ 1 ⊕ у = ху ⊕ х ⊕ 1;
x ~ y = xy ∨ xy = x yxy ⊕ xy ⊕ xy = xy ⊕ xy =
= ху ⊕ (х ⊕ 1)(y ⊕ 1) = ху ⊕ ху ⊕ х ⊕ у ⊕ 1 =
= х ⊕ у ⊕ 1.
Приклад. Зобразити поліномами Жегалкіна логічні функції імплікацію (→) і еквівалентність (~).
Слайд 57Розв'язок. Проаналізуємо структуру формул, що виведені у попередньому прикладі.
x →
Імплікація (→) є нелінійною функцією,
x ~ y = х ⊕ у ⊕ 1.
Еквівалентність (~) — функція лінійна.
Приклад. Визначити, чи лінійні функції імплікації (→) і еквівалентності (~).
Слайд 58Розв'язок. Побудуємо поліном Жегалкіна функції f(х, у, z), використовуючи такі тотожності:
f(х, у, z)= (х ∨ у) →z = = =
= (ху ⊕ х ⊕ y ⊕ 1)(z ⊕ 1) ⊕ (ху ⊕ х ⊕ y ⊕ 1) ⊕ z ⊕ 1 =
= хуz ⊕ хz ⊕ уz ⊕ 1∧z ⊕ ху∧1 ⊕ х∧1 ⊕ у∧1 ⊕ 1∧1 ⊕ ⊕ ху ⊕ х ⊕ у ⊕ 1 ⊕z ⊕ 1 =
= xyz ⊕ хz ⊕ yz ⊕ z ⊕ ху ⊕ х ⊕ y ⊕ 1 ⊕ ху ⊕ х ⊕ у ⊕
⊕ 1 ⊕ z ⊕ 1 = хуz ⊕ хz ⊕ уz ⊕ 1.
Функція f(х, у, z) = (х ∨ у) →z не є лінійною, оскільки її поліном Жегалкіна містить кон'юнкції змінних.
Приклад. Дослідити на лінійність функцію
f(х, у, z) = (х ∨ у) →z.
Слайд 59Побудова поліному Жегалкіна
методом невизначених коефіцієнтів
Метод невизначених коефіцієнтів засновано на
Приклад. Побудувати поліном Жегалкіна для функції f13(x, у) — імплікації, використовуючи метод невизначених коефіцієнтів.
Слайд 60Розв'язок. Запишемо поліном для даної функції у вигляді суми за модулем
f13(x, у) = х → у = а1ху ⊕ а2х ⊕ а3у ⊕ а4,
де коефіцієнти а1, а2, а3, а4 приймають значення з множини {0, 1} і визначають присутність або відсутність елементарної кон'юнкції в поліномі.
Шукаємо послідовно значення коефіцієнтів, підставляючи значення змінних і функції на різних інтерпретаціях:
f13(0, 0) = 0 → 0 = 1,
1 = а1 ∧ 0 ∧ 0 ⊕ а2 ∧ 0 ⊕ а3 ∧ 0 ⊕ а4 = а4
а4 = 1;
Слайд 61f13(0, 1) = 0 → 1 = 1,
1 = а1 ∧
а3 = 0;
f13(1, 0) = 1 → 0 = 0,
0 = а1 ∧ 1 ∧ 0 ⊕ а2 ∧ 1 ⊕ а3 ∧ 0 ⊕ 1 = а2 ⊕ 1
а2 = 1;
f13(1, 1) = 1 → 1 = 1,
1 = а1 ∧ 1 ∧ 1 ⊕ 1 ∧ 1 ⊕ 1 ∧ 0 ⊕ 1 = а1 ⊕ 1 ⊕ 1 = а1,
а1 = 1.
Підставивши одержані значення коефіцієнтів одержуємо поліном Жегалкіна для функції f13:
х → у = а1ху ⊕ а2х ⊕ а3у ⊕ а4 = 1∧ху⊕1∧х⊕0∧у⊕1 =
= ху ⊕ х ⊕ 1 .
Слайд 62Функції, що зберігають нуль та одиницю
Булева функція f(x1, x2, ...,
Булева функція f(x1, x2, ..., хn) називається функцією, що зберігає 1, якщо на одиничному наборі вона дорівнює 1: f(1,1, .... 1)=1.
Функції х ∧ у і х ∨ у зберігають 0, оскільки 0 ∧ 0 = 0 і 0 ∨ 0 = 0. Крім того, дані функції також зберігають 1, оскільки 1 ∧ 1 = 1 і 1 ∨ 1 = 1. Функція х не зберігає 0 і не зберігає 1, оскільки 0 = 1, 1 = 0.
Слайд 63 Приклад. Визначте, чи зберігає 0 та 1 функція f(x, у, z)
f(0, 0, 0) = 0 ∨0 ∧0 = 0 ∨ 1 ∧ 1 = 0 ∨ 1 = 1, f(1, 1, 1)=1 ∨1 ∧1 = 1 ∨ 0 ∧ 0 = 1 ∨ 0 = 1.
Отже, дана функція зберігає 1 і не зберігає 0.
Слайд 64 Розглянемо важливий клас булевих функцій — монотонні булеві функції. Для цього
α ≤ β, якщо аi ≤ bi для всіх і = 1, ..., n.
Якщо хоча б для однієї пари (аi,bi) відношення аi≤bi не виконується, то відповідні їм набори α i β у відношенні порядку не беруть участі, тобто є непорівнянними, наприклад, (0, 1) і (1, 0).
Булева функція f називається монотонною, якщо для будь-яких пар наборів значень змінних (а1,а2,...,аn) і (b1,b2,...,bn), для яких виконується відношення (а1,а2,...,аn) ≤ (b1,b2,...,bn), правильна і нерівність f(а1,а2,...,аn) ≤ f(b1,b2,...,bn).
Монотонні функції
Слайд 65 Приклад. Дослідити на монотонність функцію
f(x, y) = x ∧ у.
Розв'язок.
(0, 0) ≤ (0, 1), f(0, 0) = 0, f(0, 1) = 0, f(0, 0) ≤ f(0, 1).
(0, 0) ≤ (1, 0), f(0, 0) = 0, f(1, 0) = 0, f(0, 0) ≤ f(1, 0).
(0, 0) ≤ (1, 1), f(0, 0) = 0, f(1, 1) = 1, f(0, 0) ≤ f(1, 1).
(0, 1) ≤ (1, 1), f(0, 1) = 0, f(1, 1) = 1, f(0, 1) ≤ f(1, 1).
(1, 0) ≤ (1, 1), f(1, 0) = 0, f(1, 1) = 1, f(1, 0) ≤ f(1, 1).
Висновок: функція f(x, y) = x ∧ у є монотонною.
Слайд 66 Приклад. Дослідити на монотонність функцію
g(x, у) = х ⊕ у.
Розв'язок.
(0,0) ≤ (0,1), g(0,0) = 0, g(0,1) = 1, g(0,0) ≤ g(0,1).
(0,0) ≤ (1,0), g(0,0) = 0, g(l,0) = 1, g(0,0) ≤ g(l,0).
(0,0) ≤ (1,1), g(0,0) = 0, g(l,1) = 0, g(0,0) ≤ g(l,1).
(0,1) ≤ (1,1), g(0,1) = 1, g(l,1) = 0, g(0,1) ≥ g(l,1).
Висновок: функція g(x, у) = х ⊕ у не є монотонною.
Слайд 67 Теорема. Булева функція, відмінна від констант 0 і 1, є монотонною,
Приклад. Визначити, чи є функція
f(x, у, z, t) = (x ∨y)→(z ∨ t) монотонною.
Розв'язок. Виразимо f(x, у, z, t) через елементарні функції булевої алгебри:
(x ∨y)→(z ∨ t) = = ху ∨ z ∨ t.
Одержана формула булевої алгебри не містить заперечень, отже функція f(x, у, z, t) є монотонною.