- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое описание случайных величин. (8 класс) презентация
Содержание
- 1. Математическое описание случайных величин. (8 класс)
- 2. Случайный опыт (случайный эксперимент) – условия
- 3. Однократное бросание кости: Число элементарных событий
- 4. Равновозможные события – шансы которых одинаковы
- 5. Вероятности элементарных событий Для равновозможных элементарных событий
- 6. Свойства вероятностей элементарных событий Рассмотрим случайный
- 7. Свойства вероятностей элементарных событий Проведём эксперимент
- 8. Благоприятствующие элементарные события Определение. Элементарные события,
- 9. Пример 2. Игральную кость бросают дважды.
- 10. Вероятности событий Вероятность случайного события А –
- 11. Вероятности событий Пример 1. Автомобиль подъезжает к
- 12. Опыты с равновозможными элементарными событиями Определение.
- 13. Опыты с равновозможными элементарными событиями Правило.
Слайд 18 класс.
Тема 2. Математическое описание
Случайных величин
©Максимовская М.А., Центр образования №109,
Слайд 2
Случайный опыт (случайный эксперимент) – условия и действия, при которых может
В результате случайного опыта наступает только одно
элементарное событие.
Элементарное событие нельзя разделить
на более простые события
Выпало чётное число очков
Выпало четыре очка
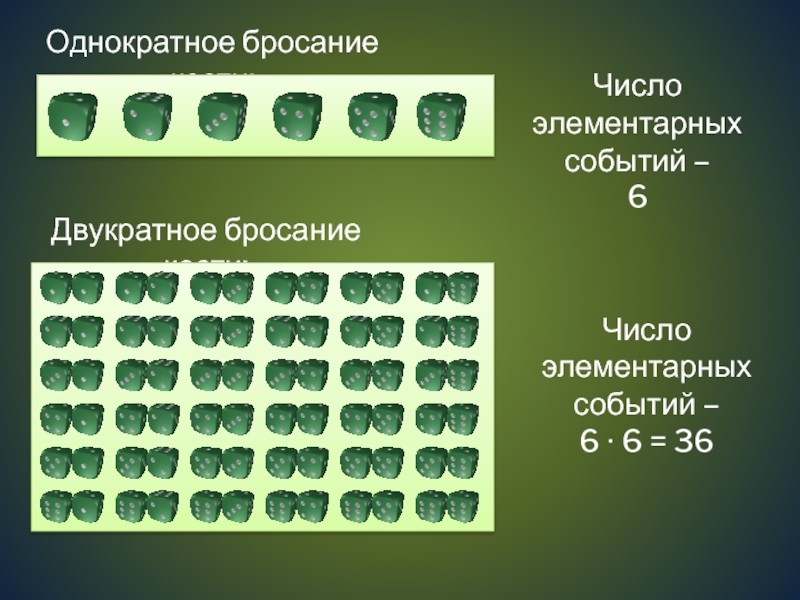
Слайд 3Однократное бросание кости:
Число элементарных событий –
6
Двукратное бросание кости:
Число элементарных событий –
6
Слайд 5Вероятности элементарных событий
Для равновозможных элементарных событий
Число этих событий - N
Вероятность каждого
1
N
Слайд 6Свойства вероятностей элементарных событий
Рассмотрим случайный эксперимент, в котором a, b, c,
Обозначим вероятности этих элементарных событий - P(a), P(b), P(c), … .
P – число от 0 до 1
P(a) + P(b) + P(c) + … . = 1
Сумма вероятностей всех элементарных событий = 1
Слайд 7Свойства вероятностей элементарных событий
Проведём эксперимент N раз –
событие a произошло
Тогда N(a) + N(b) + N(c) + … = N
N(a) + N(b) + N(c) + … = 1
N N N
Сумма частот элементарных событий:
Слайд 8Благоприятствующие элементарные события
Определение. Элементарные события, при которых наступает событие А, называют
Пример 1. Андрей (А), Борис (Б) и Владимир (В) встают в очередь.
Возможные элементарные события:
АБВ, АВБ, БВА, БАВ, ВАБ, ВБА.
Событие «В стоит первым» наступает, если случилось одно из двух элементарных событий: ВАБ, ВБА.
Событию «В стоит первым» благоприятствуют события ВБА и ВАБ.
Событию «Б стоит впереди А» благоприятствуют элементарные события:
БАВ, БВА, ВБА
Слайд 9Пример 2. Игральную кость бросают дважды.
Таблица элементарных событий этого опыта:
1.
2. Событие «произведение очков при двух бросках равно 12». Найти благоприятствующие элементарные события.
Слайд 10Вероятности событий
Вероятность случайного события А – Р(А), В – Р(В) и
Вероятности Р(а), Р(b), P(c), Р(d), … - вероятности элементарных событий, благоприятствующих соответствующим случайным событиям.
P(А) = Р(a) + P(b) + P(c) + Р(d) +… .
0 ≤ P(А) ≤ 1
Невозможное событие
Достоверное событие
Пример 1. Максим играет с Иваном в шахматы. Вероятность выигрыша для Максима – 0,001, вероятность ничьей равна 0,01. Найти вероятность события А «Максим не проиграл».
Решение. Событию А благоприятствуют элементарные события «Максим выиграл» и «партия закончилась вничью». Тогда:
Р(А) = 0,001 + 0,01 = 0,011.
Правило вычисления вероятности события А:
Где a, b, c, d, … - элементарные события, благоприятствующие случайному событию А.
Слайд 11Вероятности событий
Пример 1. Автомобиль подъезжает к перекрёстку.
Вероятность элементарного события «автомобиль
вероятность элементарного события «автомобиль свернёт влево» равна 0,3,
вероятность элементарного события «автомобиль поедет прямо» равна 0,18.
Найти. Вероятность события А «автомобиль не поедет обратно».
Решение. Событию А благоприятствуют все три перечисленных элементарных события. Тогда:
Р(А) = 0,5 + 0,3 + 0,18 = 0,98.
Слайд 12Опыты с равновозможными элементарными событиями
Определение. События, которые имеют одинаковые вероятности, называют
Равновозможные элементарные события – равновероятны.
Вероятности этих событий в сумме –
1.
Вероятность каждого события (если их количество N) равна
1
N
Если случайному событию А благоприятствуют N(A) элементарных событий, то
Р(А) = N(A)
N
Слайд 13Опыты с равновозможными элементарными событиями
Правило. Пусть все элементарные события опыта равновозможны.
Пример. Найти вероятность события А «сумма очков равна 6».
Решение.
Число благоприятствующих событий N(A) = 5. Общее число событий N = 36.
Р(А) = N(A) = 5
N 36